基于过程集成的迫击炮内弹道参量优化

王镒磊，姚养无，李树军

(1.中北大学 机电工程学院，太原 030051;2.宁波军鸽防务科技有限公司，浙江 宁波 315000)

0 引言

迫击炮是一种以曲射为主的滑膛火炮，结构简单、操作方便、可几乎无死角射击遮蔽物后方目标[1]。常规火炮多数是从炮尾完成炮弹的装填、击发及退壳操作，而迫击炮则是采用炮口装填的方式发射带有尾翼的整个炮弹，可配备包括杀伤爆破弹在内的多种炮弹，无需退壳，常用来摧毁敌方工事及隐蔽在山丘后方的有生力量，有时也用来发射照明弹等，在战争中发挥了不可替代的作用。迫击炮这些战术上的优势均源自它特殊的弹道性能，而内弹道参数直接影响着迫击炮的弹道性能。对于包括迫击炮在内的绝大多数身管武器，其内弹道都是一个及其复杂的过程，包含了多种物理及化学变化，限于计算机技术的发展及该领域的认知水平，设计人员在对武器的内弹道进行设计时仍按照以往的设计经验进行设计，设计完成后组织相关的试验进行验证。若试验结果能够满足相关的战技术指标要求，则此方案便作为预选方案确定下来，否则重新进行方案设计及试验验证直到能够满足指标要求为止。这样的设计方法虽然最终能够得到满足要求的方案，但是大大增加了设计成本，不仅浪费了大量的人力和物力，得到的方案也只是可行方案，并非最优方案。在迫击炮内弹道设计过程中，其内弹道基本理论是整个设计过程的关键所在，内弹道计算的准确性直接决定了迫击炮的整个弹道性能。迫击炮的内弹道设计计算均是基于基本内弹道理论进行的，对于身管武器内弹道计算方程，传统的解法都是基于图解法、经验法等进行求解，这些解法均进行了一定程度的简化，使得最后的计算结果与实际中测试的结果具有较大的出入，不仅无法得到武器真实的弹道性能参量，对于后续出现的问题也无法得到快速的解决[2]。随着计算机技术的发展，各种计算机辅助设计软件的出现极大地提高了设计人员的工作效率，内弹道作为身管武器系统的核心，利用数值方法进行仿真计算成为了求解内弹道模型的主要方法，但是相比于普通火炮，迫击炮的内弹道模型更加复杂，涉及的参数更多，利用编程技术求解不仅增加了求解难度，而且极易出错。Simulink只需要通过简单的拖拽就可以完成复杂模型的仿真求解，成为了解决复杂数学模型的强有力手段[3]。

在迫击炮内弹道设计过程中，内弹道的性能是多个参数综合作用的结果，经试验验证得到的满足指标要求的方案只是可行方案且不唯一，运用现代研究方法及相关的专业理论，综合各指标及相关约束等因素选出具有最优弹道性能的内弹道参数是迫击炮武器系统优化设计的关键。虽然内弹道优化设计过程要比单纯的内弹道设计更加复杂，但经过优化得到更加科学的内弹道参数是武器设计人员所追求的最终目标。曾宪刚[2]等利用复合形法对某型迫榴炮进行了单个目标内弹道优化设计，得到了较为理想的内弹道性能，但迫榴炮内弹道常常涉及多个性能参数，且各个参数之间相互影响、相互制约，单个目标的优化忽略了参数间的相互作用，优化后的弹道性能与无法达到预期的效果。在对多个目标函数进行优化设计时，复合形法等方法也常因较差的全局搜索性而难以达到理想的优化效果[4]。随着优化理论的发展，以遗传算法[5]为代表的许多智能优化算法应用在内弹道优化设计中。何新佳[6]等利用多目标蝙蝠算法对内弹道进行了优化研究,提升了内弹道性能及火炮发射安全性；肖剑[7]等利用Pareto遗传算法对内弹道进行了多目标优化设计，得到了较优的内弹道参数。这些智能优化算法在内弹道优化设计中取得了较好的效果，但在优化设计过程中，该类智能优化算法均需要利用编程技术进行编译，程序过程繁琐，不仅增加了计算时间，还易产生错误。计算机技术的发展使得过程集成优化技术被越来越多的应用在优化设计领域[8]，在武器内弹道优化设计中，过程集成技术的应用还比较少，因此本文以迫击炮为研究对象，针对迫击炮内弹道计算及优化设计中存在的不足，笔者将通过MATLAB/Simulink进行迫击炮内弹道基本模型的求解，并基于过程集成优化技术对其内弹道参数进行寻优计算。

1 迫击炮内弹道数学模型

1.1 迫击炮发射原理

迫击炮的结构十分简单，由身管、座板、架体及瞄具等构成，不仅有较强的杀伤效果，而且在行军时座板与身管可分解，能够快速进行阵地转移，具有较好的机动性，在战争中有着不可替代的作用。在瞄准要打击的目标后，由射手将带有尾翼的炮弹从炮口滑下，通过弹丸定心部与炮管内壁之间的间隙及炮弹自身的重量滑落到炮管底部使得炮弹的底火撞击击针，而后底火点燃基本装药，基本装药点燃辅助装药并在弹体外部的闭气环形成较大的压力推动弹丸向前运动，炮弹上的尾翼能够保证弹丸在出炮口后具有较为稳定的飞行姿态。

1.2 迫击炮内弹道特点及基本假设

迫击炮的弹道性能取决于其特殊的装药结构，与普通火炮不同的是，迫击炮弹的装药是由基本装药和辅助装药两部分构成，其装药结构如图1所示。

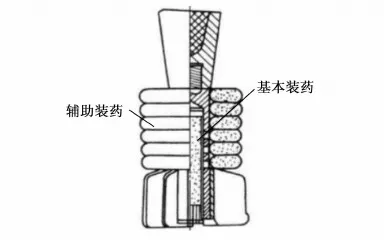
图1 迫击炮装药结构示意图

由图1可知，迫击炮弹的基本装药是装填在药管内，而辅助装药则是分布在尾管周围的等质量药包，辅助装药通过基本装药点燃。

依据迫击炮的装药结构及射击原理，迫击炮内弹道具有以下特点：

1)迫击炮的发射原理类似于高低压发射原理，其点火情况要比普通火炮复杂的多，影响内弹道性能的因素也较多，基本装药以及辅助装药等结构对于整个装药的一致性有着直接的影响；

2)迫击炮弹丸定心部与炮膛内壁之间存在的间隙会造成火药气体的外泄，进一步影响武器系统的射击性能；

3)迫击炮弹药多为薄火药且具有较小的装填参量，使得整个火药燃烧结束位置与最大膛压发生的位置几乎重合；

4)迫击炮的弹丸运动速度和膛内压力都比较小，弹丸击发后产生的火药气体与炮膛内壁长时间接触导致较大的热损失。

根据迫击炮的装药结构及其内弹道特点提出以下假设[9]：

1)传火孔打开前，基本装药作定容燃烧。传火孔打开后，基本装药燃烧产生的火药燃气从孔中流出并点燃辅助装药。在基本装药未燃完前，二者混合燃烧。当基本装药燃完后，辅助装药单独燃烧至燃完。

2)基本装药和辅助装药按各自的燃烧规律燃烧，燃速公式采用指数燃烧定律。

3)通过减小火药力的方法间接修正热损失的影响。

4)气体从间隙中流出时，满足临界状态条件。

1.3 迫击炮内弹道基本方程

依据上述基本假设，可将迫击炮内弹道过程分为以下3个阶段。

第一阶段：在基本装药燃烧产生的火药气体未冲破传火孔前，基本装药在尾管中作定容燃烧。

以传火孔打开时刻为计算起点，破孔时基本装药相关初值为：

(1)

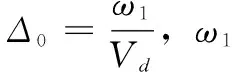
第二阶段：当火药燃气冲破传火孔后，两种装药作混合燃烧，其基本方程为：

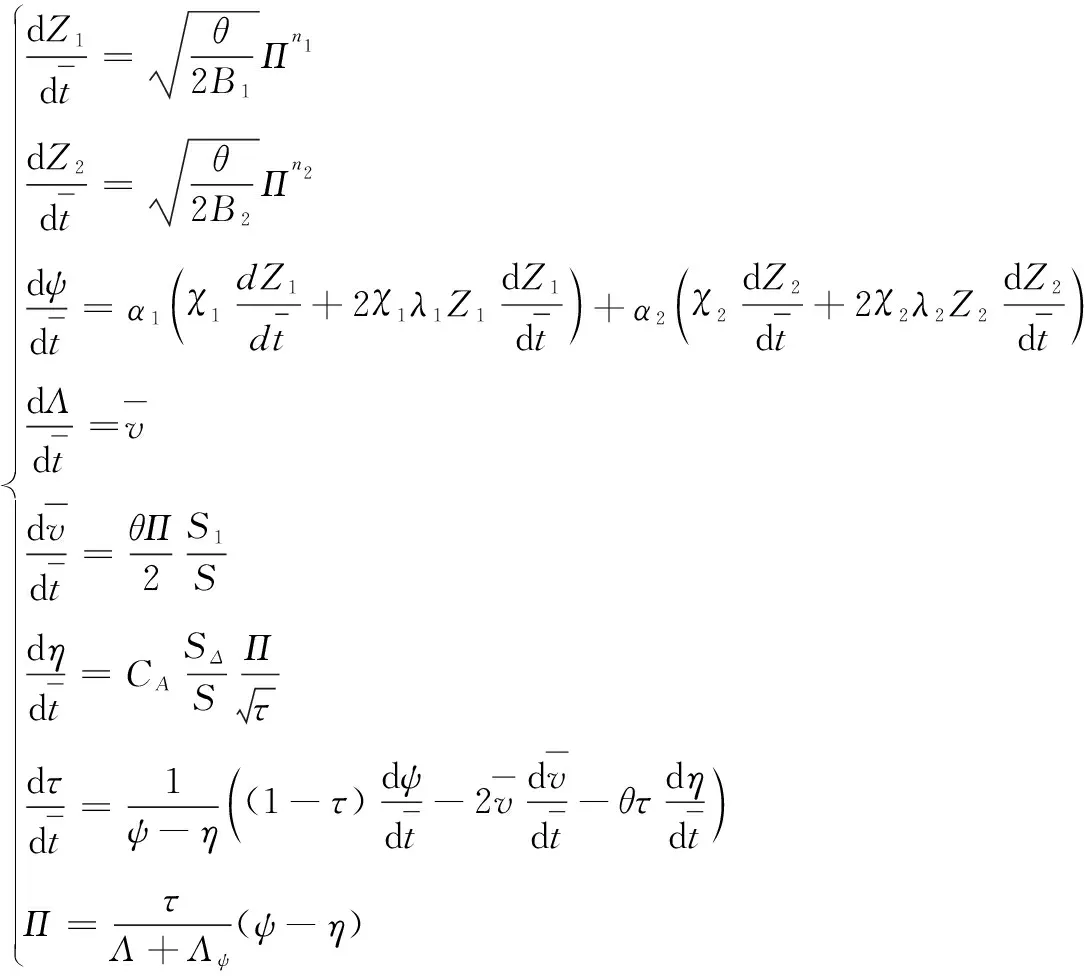
(2)

其中：

(3)

(4)

(5)

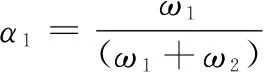
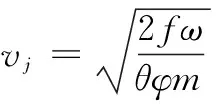
第三阶段：当基本装药燃烧完毕后，辅助装药独自燃烧至燃完。令第二阶段方程组中基本装药的相关参数为零则表示辅助装药独自燃烧[10]。

初始条件：

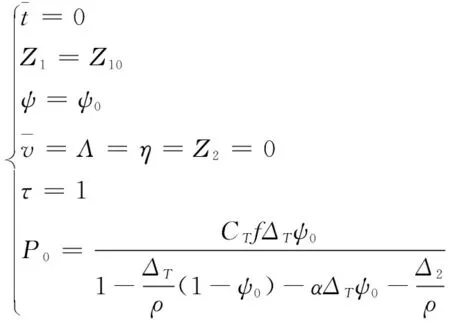
(6)

1.4 迫击炮内弹道仿真计算

迫击炮内弹道数学模型是由微分方程与代数方程组成的微分代数方程组，常规解法是利用四阶龙格库塔法进行编程求解，由于迫击炮的内弹道所涉及的参数较多，且参数间的相互关系错综复杂，在编写代码时易产生逻辑上的错误。相比于编程技术，Simulink有着清晰的结构和流程，只需通过简单的拖拽便可实现复杂的方程运算，在出现问题时也可快速检查错误，既提高了计算效率，又减小了出错率。迫击炮内弹道计算过程中所涉及的原始参数及初值运算，仍旧需要以脚本的方式写入MATLAB的工作空间，在运行 Simulink进行仿真计算时供以调用。本文基于MATLAB/Simulink建立的迫击炮内弹道仿真模型如图2所示[11]。

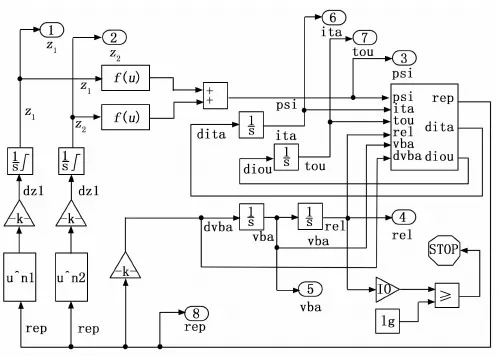
图2 迫击炮内弹道仿真模型

运行仿真时，选泽四/五阶龙格-库塔法，采用合适的计算步长，仿真结束后得到迫击炮在射击过程中的的膛内压力、弹丸运行速度随时间变化关系如图3～4所示。

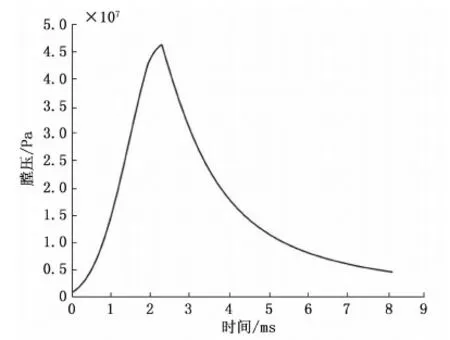
图3 膛压随时间变化曲线

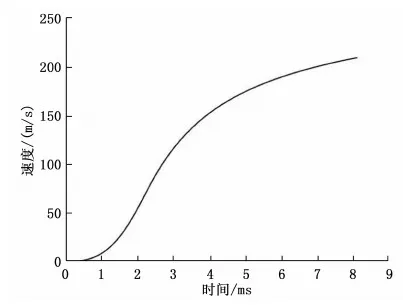
图4 速度随时间变化曲线

由数值仿真计算结果可以得到：迫击炮内弹道过程中的最大膛压为46.284 Mpa，炮口速度为208.29 m/s，且通过计算数据发现火药燃烧结束时的位置几乎与内弹道过程中的最大膛压发射位置一致，符合迫击炮的内弹道特点。该迫击炮内弹道经实验测得的最大膛压为42.6～43.6 Mpa，弹丸运动到炮口速度为202～205 m/s[8]。在一定的误差范围内，数值仿真计算结果与实验结果具有较好的一致性，证明基于MATLAB/Simulink所建立的迫击炮内弹道求解模型是正确的，为内弹道的进一步优化奠定了基础。

2 过程集成优化设计方法

过程集成优化设计是计算机辅助研究的一项新技术。它通过接口集成技术、数值仿真技术等将实际工程研究中所要用到的商业软件集成在同一平台中并同时运行多个不同的软件，实现整个仿真、优化流程的全自动化，能够极大地提高优化效率[12]。该项技术最早运用于航空航天领域，在进行航空发动机设计初期，由于整个系统涉及到多个复杂的仿真程序，各个仿真程序间存在着错综复杂的参数耦合关系，且系统优化设计中的约束关系相当苛刻，即使花费相当长的时间进行优化计算仍无法得到理想的结果，甚至还常常因数据传递问题使得计算中断。为了应对这一难题，唐兆成博士利用分布式计算机技术集成整个复杂系统的多个子系统，采用组合优化策略以获得系统整体最优解，不仅提高了产品的整体性能，还极大地缩短了产品的研制周期。在武器系统设计过程中，武器也是包含多个子系统的复杂系统，设计人员常常需要借助各种辅助软件建立分析计算模型，且各模型需要在不同软件之间进行数据交换，不仅使得分析步骤繁琐，还会因数据交换导致各种分析误差以及单位上的不一致等问题。过程集成技术能够有效地避免上述问题，自动实现不同软件间数据的传递。

ISIGHT是当前最具代表性的过程集成优化设计平台之一，能够集成绝大多数工程中所用到的商业软件，通过简单的拖拽就可以将复杂的仿真流程组织在统一的框架中并自动驱动仿真的进行[13]，用户可根据工程实际问题设定和修改设计参量，自动进行循环迭代，将工程设计人员从无用的重复劳动中解放出来。除此之外，用户可根据所研究问题的特点自行组合多种算法形成优化策略，所设定的设计变量、目标函以及约束条件等的迭代计算过程也可通过后处理工具直观地展现出来，如若在计算过程中发现某些数据错误，可直接结束优化过程并重新修改优化参量及优化算法，而后重新进行迭代求解。优化完成后，可通过多种后处理工具进行多种可行方案对比。在船舶领域，ISIGHT多用于船体布局及结构的优化设计、蒸汽轮机设计等；在兵器领域，ISIGHT用于导弹武器系统的多学科优化设计以及装甲车液力变矩器的优化设计等，且均取得了较好的效果。利用ISIGHT进行集成优化的一般过程如图5所示。

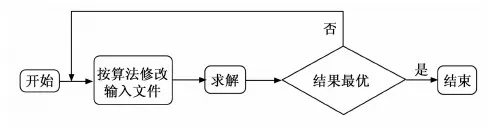
图5 ISIGHT集成优化的一般过程

由图5可以看出，利用ISIGHT进行集成优化的过程实质上就是在仿真软件自身分析运行的基础上，通过改变输入文件的参数以实现模型的修改，避免了传统实际工程优化设计过程中的“设计-评估-改进”的循环[14]，实现了在规定的约束条件下自动进行参数修改及寻优求解，可极大地提高优化效率。本文基于ISIGHT平台集成MATLAB/Simulink软件对迫击炮内弹道进行优化研究。

3 多目标优化理论

3.1 多目标优化数学模型

在实际的工程问题中，所研究的对象往往是由多个分系统组成的复杂系统，即使是单个分系统也必定会涉及到多个性能参数，且各个性能之间存在着相互制约、相互耦合关系。单一目标的优化设计虽然在一定程度上能很好地使其达到最优，但由于没有考虑各参数之间的相互影响，必然导致其他性能参数劣化的现象，这对于实际工程往往是极为不利的，尤其是对于武器系统，一味地追求某个指标最优必然会导致其余指标弱化，在实际作战中甚至会威胁到士兵的生命安全。因此在进行优化设计时，必须综合考虑多个指标，在规定的约束条件下进行多个目标的优化计算。多目标优化的数学模型可表述为：

(7)

式中，x为优化设计变量；F(x)为目标函数；gj(x)、hk(x)为约束条件。

3.2 多目标优化方法

在处理多目标优化问题中所采用的方法大体上可分为直接搜索法和群体搜索法两大类。

3.2.1 直接搜索法

直接搜索法是一类衍生于数学理论的基本方法，常见的有线性加权求和法以及ε约束法等。线性加权求和法也称归一化方法，即通过将各个目标函数通过一定的权重因子相加在一起，使得多目标问题转化为单目标问题进行求解。这种方法计算简单，能够保证在求解过程中收敛于某个确定值，即获得一个确定的最优解。但由于目标函数的权重因子需要人工进行定义，在很大程度上取决于决策者的主观判断，使得权重不易确定，在优化设计中常常与所期望的结果相差甚大，难以得到符合实际问题的最优解。而ε约束法则是将多个目标函数中的其中一个作为优化目标，其余目标函数则作为约束条件，即将多目标问题转化为带约束条件的单目标问题，通过改变ε值的大小来获得最优解。同线性加权法类似，该方法也能够在较短的时间内获得唯一确定的最优值，但由于计算过程中对于ε值的依赖性过大，且在复杂问题中难以快速确定合适的ε值，使得设计人员常常需要在多个ε值之间不断的尝试，极大地降低了优化效率。除此之外，直接搜索法常常要求所研究的问题在一定范围内满足连续等条件，而在实际的问题当中，所研究的对象都较为复杂，很多情况下采用直接搜索法无法进行求解。在早期的多目标优化问题中，由于计算机技术及优化理论的发展限制，只能通过这些方法通过不断的尝试找到一组较为满意的优化值。

3.2.2 群体搜索法

针对多目标优化设计过程中直接搜索法所面临的不足以及多目标优化问题的不断复杂化，为了能够得到符合工程实际的优化效果，人类通过学习、模拟自然界中的生物进化现象探索出了多种可应用于多目标优化问题的算法，也称为进化算法，在面向多个目标时能够表现出较好的全局搜索性。其中以遗传算法、改进的遗传算法、粒子群算法和模拟退火算法等最具代表性。该类算法常用于大型复杂的多系统多目标优化设计中，利用该类算法在处理复杂系统的多个目标优化问题时，能够在整个系统中进行全局搜索，受外界影响小且具有较好的稳定性。而且无需进行多目标向单目标的转化，不仅避免了因设计人员的主观因素造成优化结果不合理，还可在未知是否可微的情况下进行寻优计算，在各个领域得到了广泛的应用，成为了解决多目标优化问题的强有力工具。

基于上述相关理论，以迫击炮内弹道基本模型为基础，结合多目标进化算法对其弹道性能进行优化设计以获得最优的弹道性能。

4 迫击炮内弹道多目标优化模型

4.1 内弹道多目标优化数学模型

迫击炮内弹道优化设计就是根据武器所要求的战术技术指标，选择设计变量与目标函数，在规定的约束条件下选择合适的智能优化算法进行寻优计算。在迫击炮内弹道设计过程中，威力是武器设计人员追求的首要目标，弹丸的速度越大则意味着威力越大，然而速度增大必然会导致膛压升高，不仅降低武器寿命，还可能发生炸膛事故，严重时会对操作者造成致命威胁。膛压和初速是身管武器内弹道的重要性能指标，且二者之间相互影响，相互制约。因此在提高弹丸速度的同时尽可能减小膛内压力是迫击炮内弹道优化设计的关键[15]。因此本文以最大膛压和炮口速度作为优化目标，是一个多目标优化问题。其数学模型可表示为：

(8)

在发射迫击炮弹时，为使弹丸顺利滑下并且有足够的动能撞击击针，弹丸定心部与炮膛内壁存在一定的间隙SΔ，间隙的存在不仅会造成能量的外泄，增加了武器射击过程中的热损失，还会对膛内压力和弹丸速度产生重要的影响，进而影响武器的射击精度，因而间隙既要能保证弹丸能够沿身管顺利滑下，还不能过大以免造成过多的能量消耗。依据相关文献[16]，迫击炮弹的基本装药量ω1、辅助装药量ω2、药室容积V0以及弹丸质量m对于迫击炮内弹道过程中的炮口速度以及膛内压力也有着显著的影响。因此以上述5个变量作为设计变量，其数学模型可表示为：

X=(SΔ,ω1,ω2,V0,m)T

(9)

任何工程优化问题都需要在一定的约束条件下进行，迫击炮内弹道优化设计需在以下约束条件下进行。

1)在内弹道优化设计中，对于身管武器来说，为保证迫击炮具有一定的强度和使用寿命，要求其最大膛压不得超过身管材料的许用压力，即:

Pm≤[τ]

(10)

故有:

g1(X)=Pm-[τ]≤0

(11)

2)对于迫击炮来说，其炮口速度和最大膛压相对较小，为保证迫击炮的射击性能，依据枪炮内弹道学中的相关理论，其火药总装填密度Δ在40～150 kg/m3左右，而由于基本装药起传火的作用使得其装填密度Δ0很大，一般为650～800 kg/m3[8]，即,

40≤Δ≤150

(12)

650≤Δ0≤800

(13)

故有:

g2(X)=40-Δ≤0

(14)

g3(X)=Δ-150≤0

(15)

g4(X)=650-Δ0≤0

(16)

g5(X)=Δ0-800≤0

(17)

综合上述分析可得到迫击炮内弹道多目标优化数学模型的一般表达式为：

(18)

4.2 多目标智能优化算法

过程集成优化技术不仅拥有先进的软件集成接口，还提供了多种适用于不同工程问题的优化算法，包括全局优化算法、数值优化算法以及多目标优化算法等。针对本文所研究的迫击炮内弹道多目标优化问题，为规避传统的归一化方法中因设计人员主观因素对优化结果的影响[17]，以带精英策略的改进非支配排序遗传算法，即NSGA-Ⅱ对其进行寻优计算。

NSGA-Ⅱ，作为第二代多目标进化算法，是针对NSGA在寻优计算中存在的复杂程度大的改进，又称带精英策略的改进非支配排序遗传算法，通过采用(μ+λ)以实现精英策略。精英策略能够使将非支配解中的优秀个体通过特定的策略复制到下一个种群中，是优化算法能够收敛的必备因素。由于导入了“拥挤距离排序”法，能够对个体在同样的Pareto顺序层内进行排序并判别该层内的个体优劣程度，解决了第一代遗传算法非支配排序的复杂性，而且还在一定程度上拓宽了Pareto解集的分布空间，在复杂系统的多目标优化研究中体现出较好的全局探索性能。该算法基本思想为[18-19]：

1)首先需要对参数进行初始化操作，然后在所设置的搜索空间中随机产生规模为N的初始种群，通过算法所规定的非支配排序方法对随机生成的初始种群进行分层与排序操作，随后利用遗传算法的选择、交叉、变异基本操作得到第一代子代种群；

2)父代种群与子代种群从第二代开始便需要进行合并操作，在完成非支配排序的同时需要对当前每个非支配层中的个体进行拥挤度计算，最后根据上述个体的拥挤度计算结果与非支配排序关系，在该代群体中选取若干较为合适的个体组成新的父代种群；

3)在完成上述操作后，根据遗传算法所规定的选择、交叉、变异等基本操作以使新的子代种群产生。按照上述流程依次执行，直到得到满足条件的个体为止，并将最后一代得到的结果作为最终解。

相应的算法流程如图6所示。

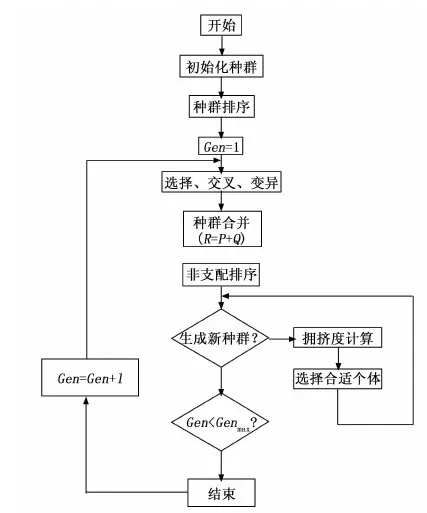
图6 NSGA-Ⅱ算法流程图

5 优化结果分析实验结果与分析

5.1 Pareto解集

在多目标优化问题中，最终得到的优化方案并不唯一，通常是连续的而且有无限多个，构成了Pareto前沿，即Pareto解[20]。由于目标函数间存在着相互矛盾的性质，一般情况下各目标函数之间是相互影响，相互制约的关系，使每个目标函数同时达到各自最优值的解是不存在的，解决多目标优化问题的最终目的只能是在各个目标之间进行协调权衡和折衷处理，使各子目标均尽可能达到最优。

计算时，设置NSGA-Ⅱ算法种群规模为12、交叉概率为0.9，经过241次优化迭代，可从后处理模块得到炮口速度与最大膛压优化历程如图7、图8所示。

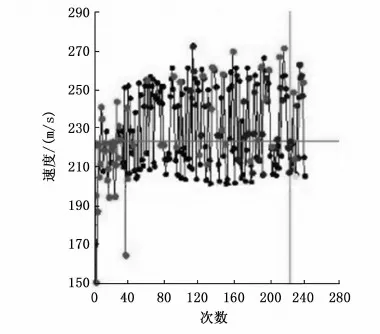
图7 炮口速度优化迭代历程

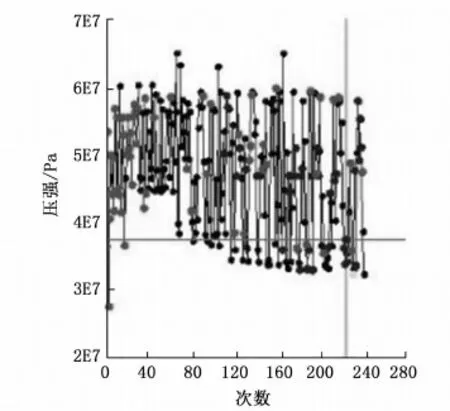
图8 最大膛压优化迭代历程

由图可知，迫击炮内弹道过程中的炮口速度和最大膛压在优化迭代过程中虽然存在震荡现象，但其变化范围较小且相对稳定。依据武器的性能要求，对Pareto前沿解集进行平衡折衷处理，选取第114步的计算结果作为内弹道多目标优化的最终结果。

5.2 优化前后仿真结果对比

优化计算完成后，迫击炮优化前后的设计参数对比如表1所示。

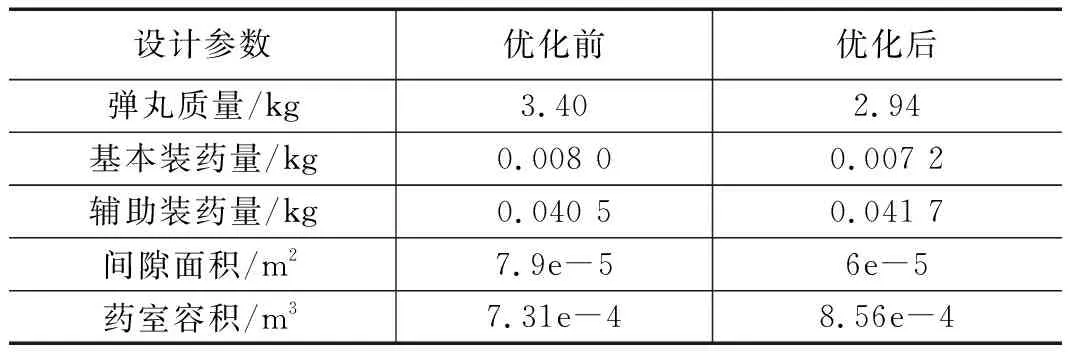
表1 优化前后设计参数变化

为了更好地验证优化后的设计参数对内弹道性能的优化效果，将优化前后的设计参数带到MATLAB/Simulink计算模型中，可得到优化前后的膛压、速度随时间变化关系如图9～10所示。

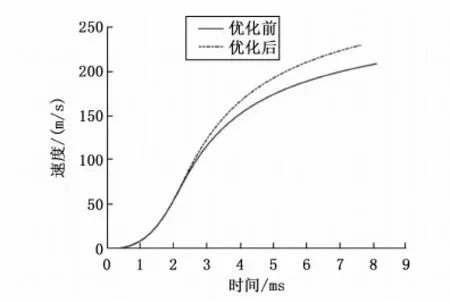
图10 优化前后速度随时间变化曲线

优化前后目标函数对比如表2所示。

表2 目标函数优化前后结果对比

通过以上图表可以得出，在满足一定约束的条件下，通过合理的优化迫击炮内弹道参量，使得其内弹道过程中的最大膛压降低了13.63%，弹丸的炮口速度提高了10.46%。在提高武器威力的同时兼顾了膛压过高的问题，不仅极大地改善了迫击炮的内弹道性能，还有效地提高了优化设计效率。

6 结束语

本文以迫击炮内弹道模型为基础，内弹道计算模型利用了MATLAB/Simulink的可视化的特点，极大地方便了复杂内弹道仿真模型的计算；同时基于过程集成优化方法进行了多目标优化设计，兼顾了迫击炮的威力与膛压，实现了迫击炮内弹道参数的最优匹配，不仅降低优化设计中的出错率，提高优化效率，还为武器的内弹道优化提供了技术参考。