基于啤酒发酵过程的时变轨迹输出反馈鲁棒模糊预测控制

俞宏磊，姜冠杰，王守亚

(1.辽宁科技大学 电子信息工程学院，辽宁 鞍山 114000;2.淮南师范学院， 电子工程学院，安徽 淮南 232000)

0 引言

啤酒作为世界三大古酒之一，由于其平顺甘醇等特点，深受人们的喜欢，近年来啤酒产量占比均高于70%。随着工业技术的不断升级，在啤酒生产领域，自动化生产逐渐取代了传统的手工生产，大大增加了酒厂的生产效率。由于啤酒生产主要依靠酵母菌的发酵，而酵母菌的发酵往往需要严格的温度限制，因此如何对啤酒发酵温度进行高精度控制成为啤酒生产的关键，受到众多科研人员和工程师的关注[1-2]。

在啤酒发酵生产过程中需要保证系统安全可靠的运行，但是实际对象通常具有不确定性、强非线性、强干扰等特性，传统控制方法对高精度控制要求存在一定的局限性。因此，先进过程控制(APC，advanced process control )技术被越来越多的科研人员所关注[3-5]。其中，模型预测控制(MPC，model predictive control)被认为是最有效的先进控制方法之一，它已经存在大量成功的工业应用案例[6-7]。MPC算法结合最优控制理论[8]、李雅普诺夫稳定性理论[9]、线性矩阵不等式技术(LMI，linear matrix inequation )[10]等理论，在系统稳定前提下对控制器进行设计，具有滚动优化等特点，增加控制器的控制精度的同时给予系统状态更多的自由度和可控性，在理论研究层面取得了众多较为丰富的成果。但是MPC对模型精度要求较高，在实际生产中，由于温度、浓度、流量等实物理量参数会随着生产要求不断变化，导致啤酒发酵过程的模型参数往往是在变化的，这种变化引起的不确定性，会降低MPC方法的控制效果。因此，鲁棒模型预测控制(RMPC，robust model predictive control )逐渐走入科研人员的视线[11-13]。RMPC充分考虑到模型的不确定性影响，采用“min-max”来降低不确定性对系统输出的影响，从而有效改善系统的控制性能。因此，结合RMPC的优势，设计控制器减少不确定性在啤酒发酵过程温度控制系统产生的不利影响，增加产品的合格率是十分重要的。

众所周知，在实际的生产过程中，线性系统是极为特殊的情况，工业过程通常具有非线性特性。由于这类系统不适用叠加原理，并且分析复杂，给控制器的设计带了极大的困难。在以往的研究中，科研人员通常采用单点线性化的方法将非线性系统在工作点进行线性化建立线性模型，并在此基础上设计线性控制器[14-15]。随着生产精度的不断提高，这种方法的局限性也不断体现，为了保证系统高精度的运行，当工作点发生变化时，通常需要现场工程师根据新的工作点建立新的模型，增加了现场工作人员的负担，并且建立新的模型通常需要大量的时间，也为企业的高效生产带来不利影响。因此，文献[16-18]在单点线性化的基础上，将模型的变化当作不确定性考虑，建立具有不确定性的模型，并设计鲁棒控制器来保证控制系统的控制效果。可惜的是上述方法针对非线性较弱的系统具有较好的控制效果，对强非线性系统的控制效果不尽人意。因此，为了得到较好的控制效果，在多点线性化的基础上，通过引入加权因子建立T-S模糊模型可以较好地逼近被控对象的非线性特性[19-20]，为具有非线性特性的啤酒发酵过程温度控制系统设计高性能非线性控制器提供新思路。

目前，先进控制方法在工业控制领域的研究取得了丰富的成果[21]，甚至有些已经应用到实际生产过程中[22-23]。但目前常见的先进控制方法均使用状态空间模型来设计控制器，导致控制器都是在假设状态已知的情况下设计的。在建模时一旦选取作为状态变量的物理量不易测量，甚至不能测量时，所设计的控制器只能停留在理论层面，并不能在实际工业过程上应用。如果想将这些方法应用于实际生产，需要大大增加建模工程师的工作量。因此，文献[24]在设计控制器的同时引入状态观测器，而状态观测器通常只能估计出当前时刻的状态，如果估计值与实际值偏差较大，轻则降低产品合格率，重则造成生产事故。因此，为了控制器的可实施性，在以往研究结果的基础上，针对啤酒发酵过程温度控制系统设计输出反馈鲁棒预测控制是十分必要的。

啤酒发酵过程的温度对酵母菌的活性起到至关重要的作用，而外界环境等因素变化造成的干扰普遍存在于控制系统中，对系统的输出会产生一定影响，如果不合理处置可能会导致系统不稳定。文献[25-26]为了使系统具有更强的抗干扰能力，在传统性能指标的基础上引入性能指标，从而增加系统的抗干扰能力。然而，随着互联网的普及以及大数据技术的加持，企业每天的生产通常会随着产品价格、原材料价格、仓库库存、能源消耗、环境因素等众多因素综合调控，从而与以往固定设定值生产的情况不同，控制系统的设定值可能会根据企业生产调控进行变化。因此，在设计控制器时如何保证系统受到外界干扰的情况下依旧稳定运行的同时保证系统输出快速跟踪变化的设定值也是提高生产效率，增加企业利润的关键。

为此，本文针对具有时变轨迹、不确定性和未知干扰的啤酒发酵过程，设计T-S模糊动态输出反馈控制器，提出一种时变轨迹输出反馈鲁棒模糊预测控制方法。该方法的主要贡献为：

1)利用具有不确定性的新型扩展T-S模糊状态空间模型来描述啤酒发酵罐温度系统，并设计相应的模糊控制器，提高系统的控制精度。

2)设计输出反馈控制器，有效避免由于状态不可测导致的控制方法实施困难的不足。

3)将设定值的变化量看作有界扰动，通过引入性能指标，增加系统对变化设定值的跟踪能力。

1 啤酒发酵罐温度系统模型建立

1.1 过程描述

啤酒发酵罐温度系统是一个典型的非线性系统，常见锥形啤酒发酵罐结构图如图1所示。其主要工作原理为通过上、中、下部的温度传感器测量相应部分的温度，通过调节冷媒水的流量改变发酵罐中的温度，从而保证酵母菌的活性，从而实现高品质、高效率的啤酒生产，增加啤酒生产企业的利润。

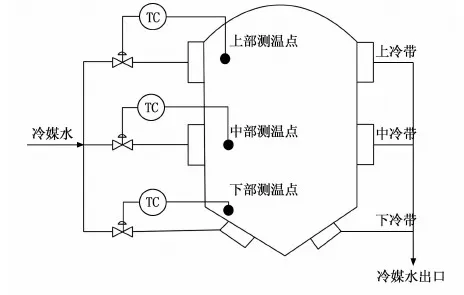
图1 锥形啤酒发酵罐结构图

首先，在文献[27]的基础上，通过理论推导构建如下机理模型：

(1)

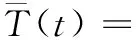
(2)

其中:CA为物料浓度；T为发酵温度；Tc为冷却液温度；V是反应器容积，单位为L；q为流量，单位为L/min；ρ为密度，单位为g/L；CP为热容,单位为J/gK；Tc为冷却液温度,单位为K；k0为速率常数，单位为min-1；E/R为指数因子,单位为K；-ΔH为反应热，单位为J/mol；UA为热传递项，单位为J/minK；V=100 L,ρ=1 000 g/L,Cp=1 J/gK,q=100 L/min,ΔH=-2×105J/mol,E/R=1 000 K,UA=1×105J/minK,k0=4.71×108min-1。

1.2 T-S模糊模型建立

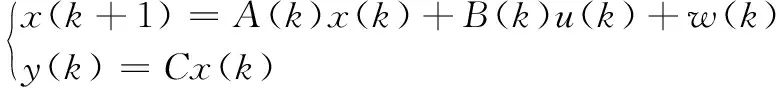
(3)

在此基础上，考虑到啤酒发酵过程的非线性特性，通过模糊规则，建立T-S模糊状态空间模型。

具体模糊规则Ri为：

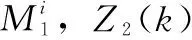
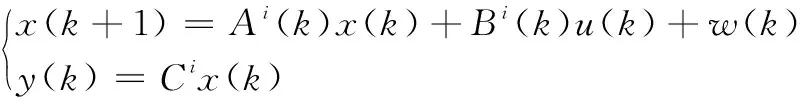
(4)

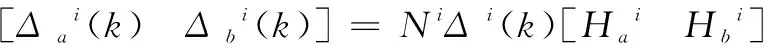
(5)

其中:ΔiT(k)Δi(k)≤I,Ni,Hai,Hbi是适当维数的已知常数矩阵，Δi(k)是与离散时间k有关不确定摄动。

然后，分别赋予子模型不同的权值hi(x(k))，该权值由推理模糊集μi(x)归一化后的得到，推理模糊集的定义如下：

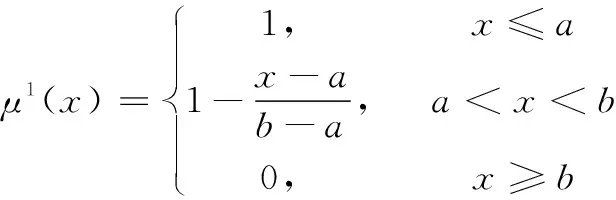
(6)

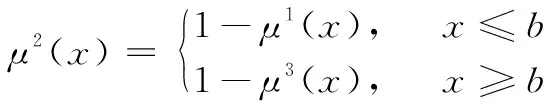
(7)

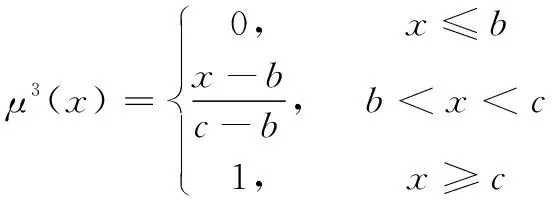
(8)

因此，将非线性工业过程去模糊化后可以表示为如下的加权状态空间模型形式：

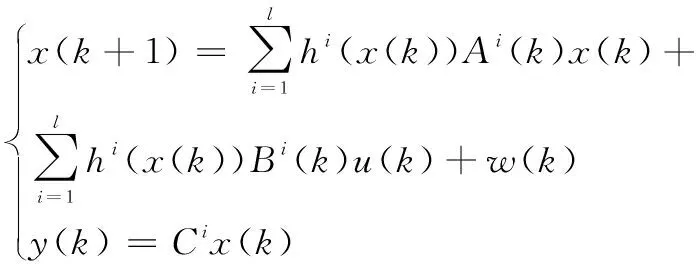
(9)

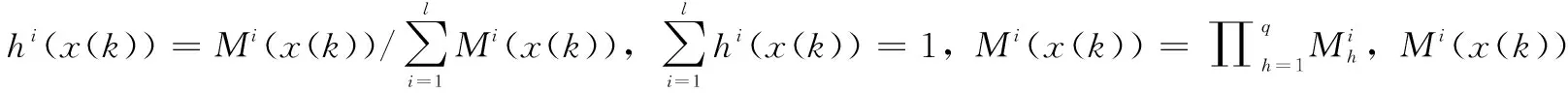
根据T-S模型中隶属度函数的3个规则，选择3个温度稳态点：0.5 ℃、5 ℃、12 ℃进行多点离散化，获得对应的T-S模糊子模型的状态空间参数分别为：

w(k)=(0.4Δ30.4Δ4)T,Δ1,Δ2,Δ3,Δ4

为在(-1,1)之间随时间变化的随机数。

注释1：该模型的优点是降低了传统单点线性化出现的模型失配问题对控制效果的影响。但是由于其需要进行多点线性化，并对多个线性化后的模型设计多个控制器，此外还需求解各个子系统的权值系数，会大大增加了计算复杂度。

1.3 新型多自由度状态空间模型建立

为了降低后期设计控制器的计算量，在式(9)基础上，利用k+1时刻的状态空间和k时刻的状态空间求差值，可以建立系统的增量式状态空间模型为：

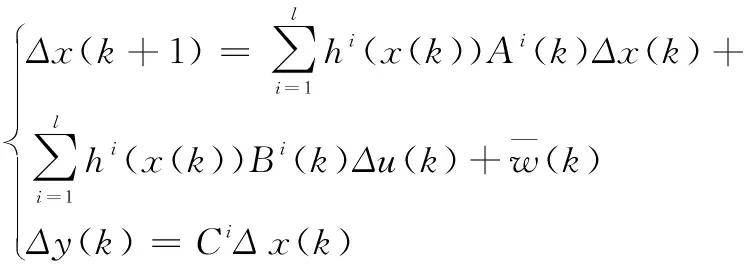
(10)

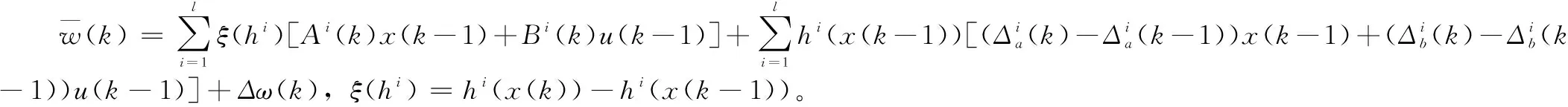
系统期望的设定值为yr(k)，定义系统的输出跟踪误差为：

e(k)=y(k)-yr(k)

(11)

通过式(10)和式(11)，考虑到设定值变化的情况，可得到离散k+1时刻的系统输出跟踪误差如下：

e(k+1)=e(k)+Δe(k+1)=

(12)

式中，Δr(k+1)=yr(k+1)-yr(k)为了提高系统的跟踪设定值的能力并增加控制器的自由度，在增量状态空间模型的基础上引入输出跟踪误差，构成新的多自由度状态空间模型如下：

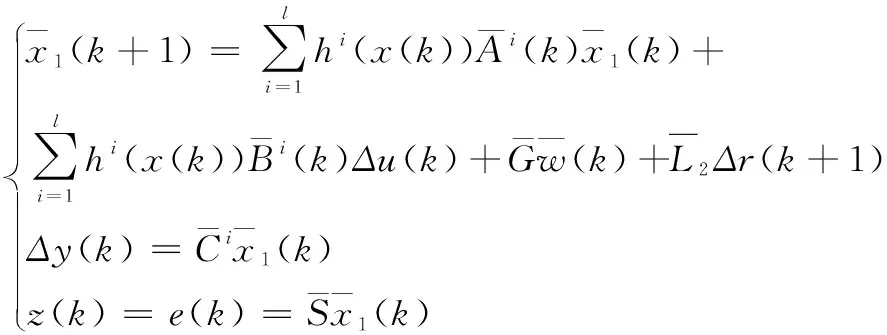
(13)

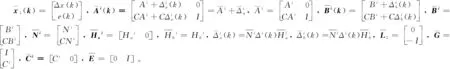
注释2：传统状态空间模型是针对被控对象的特性或者针对被控对象的输入输出方程进行设计的。基于这种模型设计出来的控制器通常的目的为保证被控对象的稳定，因此，大多数使用状态空间模型设计的控制器，最终的仿真曲线是使得被控对象的状态趋于0，从而实现系统的稳定。但设计控制器最终的目标是在实际生产中进行应用，而基于传统状态空间模型的控制器不具有使被控对象的输出跟踪设定值的能力，大大降低了控制器在实际生产中应用的可能。为了增加控制器在实际生产中的应用能力，本文在设计控制器时构建新型多自由度状态空间模型。该模型的优点为在传统状态空间模型的基础上引入输出跟踪误差作为扩展状态，使得设计的控制器在调节模型本身状态的同时，通过对扩展状态(输出跟踪误差)的调节，实现被控对象的输出跟踪设定值的效果。从而大大提高控制器在实际生产中应用的可能。

2 输出反馈鲁棒模糊预测模型控制器设计

2.1 输出反馈鲁棒模糊预测控制律

本部分的目的主要是设计输出反馈鲁棒预测控制器，引入新的控制器内部状态xc(k)，并针对每个闭环子系统设计动态输出反馈控制律，通过将求解出的控制律进行加权求和来确定系统最终的控制律，以确保非线性闭环系统的鲁棒稳定性，系统的控制律设计为如下形式：

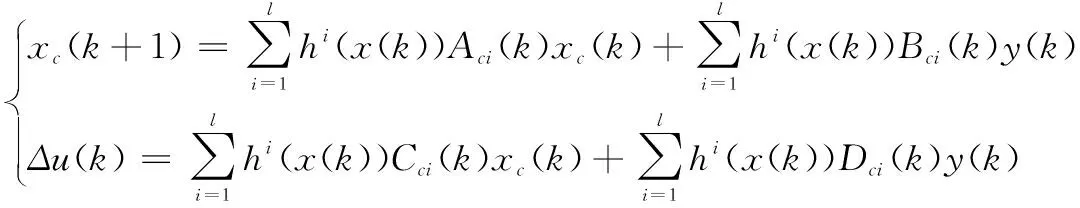
(14)

其中:xc(k)是控制器内部状态，y(k)是控制器输入Aci,Bci,Cci,Dci是需要确定的第i个子控制器参数，通过将控制律(14)代入新型多自由度状态空间模型(13)中，可得到具有权值系数的闭环系统状态空间模型如下：

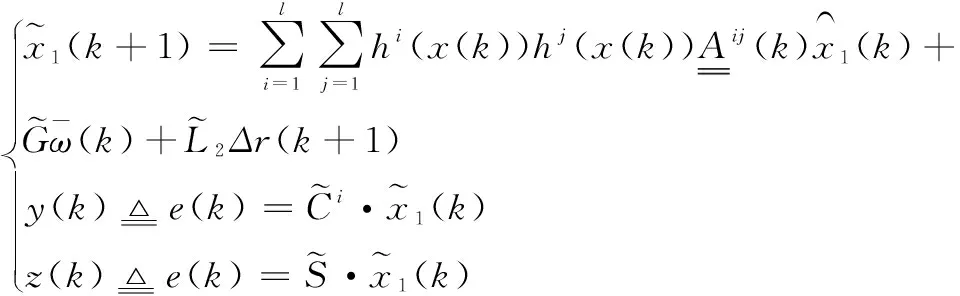
(15)

注释3：针对状态空间模型设计的控制器通常采用状态反馈的形式，即假设系统状态为可测的已知量，但在实际应用过程中，由于状态空间模型选择的系统状态通常与被控对象的特性或模型有关，导致在实际运行过程中系统状态并不是容易得到的，以往的设计是增加状态观测器来估计控制器所需的系统状态，但这会在一定程度上增加系统的复杂程度，并且状态观测器设计的准确性对控制效果的好坏起到决定性因素。本文设计的控制器采用输出反馈进行设计，从根本上避免了状态不可测问题，增加了控制器在实际生产中应用的可能性。

2.2 主要定义与引理

在推导主要定理前，首先给出后续推导过程中需要的定义和引理。

定义1：基于上述具有不确定性集的闭环模糊系统(15)，为了达到非线性系统的鲁棒预测控制目标，引入如下性能指标：

(16)

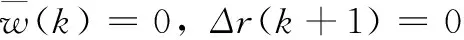
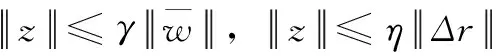
引理1[28]：设W,L和V是适当维数的矩阵，其中W,V是实数矩阵，则对于:

LTVL-W<0

可以写成如下形式:

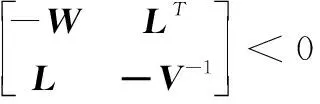
(17)

引理2[29]：假设D,F,E和M是满足M=MT的适当维数的实数矩阵，当FTF≤I，对于

M+DFE+ETFTDT<0

(18)

当仅存在标量ε>0时，使得如下不等式成立

M+ε-1DDT+εETE<0

(19)

2.3 主要定理

在此部分，根据是否存在外部干扰的情况，分别给出两种情况下控制律的设计方法。其中定理1是在没有外界干扰的情况下设计的，定理2是在有外界干扰的情况下设计的。

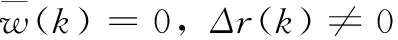
(20a)

(20b)

则可以保证非线性闭环系统(15)中的每个子系统渐近稳定，并且根据求解出的参数可以获得对应的控制律。其中，*为关于主对角线对称的元素的转置。

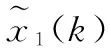
(21)

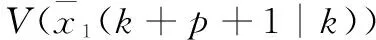
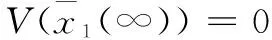
(22)

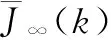
为了获取对应时刻的能量，选择构造如下李雅普诺夫能量函数：

(23)

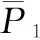
(24)

将式(21)不等式两边同时乘以θ-1，可得：

(25)

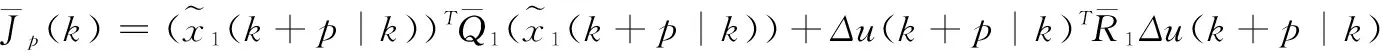
将(23)～(25)相结合，可得：

(26)

(27)

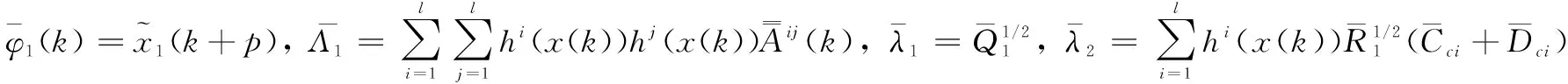
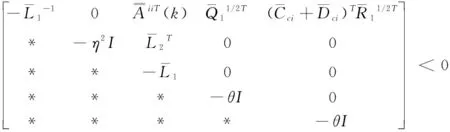
(28a)

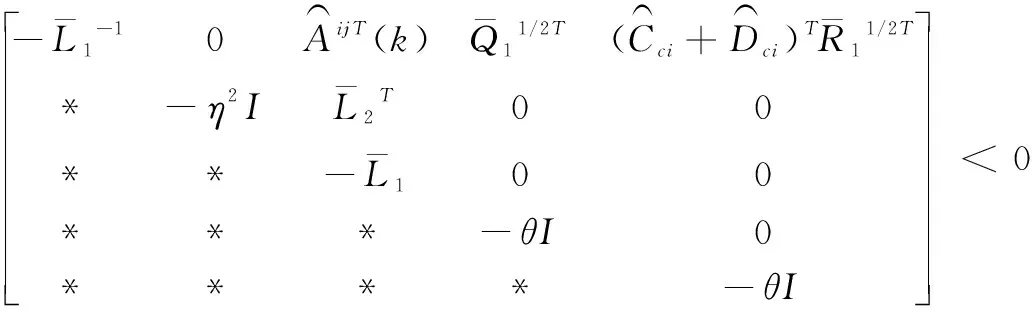
(28b)

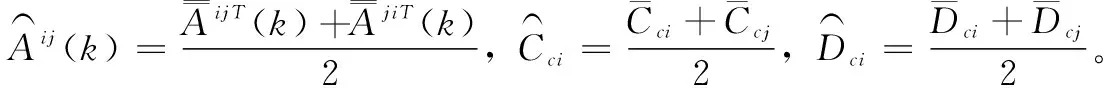
在此基础上，考虑到设定值变化对系统的影响，将设定值的变化量看作有界干扰，定义如下H∞性能指标：

(29)

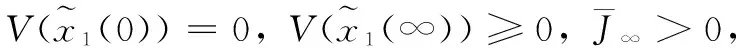
(30)

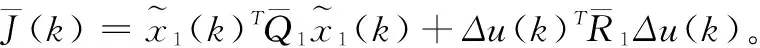
在式(30)的基础上，可得：

(31)

为了保证系统稳定需要式(31)小于0，由于式(31)为二次型形式，因此只要保证式(31)中大括号内的部分小于0即可，因此:

(32)

至此，利用引理1对式(32)进行LMI转化，并分别考虑到i=j和i≠j两种情况，即可或者式(20a)和式(20b)，定理1证毕。

注释4：在性能指标设计时，先假设没有设定值变化的情况，通过设计鲁棒模型预测性能指标保证系统的稳定性。之后将设定值的变化量看作外界有界干扰，引入H无穷性能指标增加控制系统对设定值变化量的控制能力，从而实现在设定值发生变化时，系统输出具有较快跟踪变化设定值的能力。

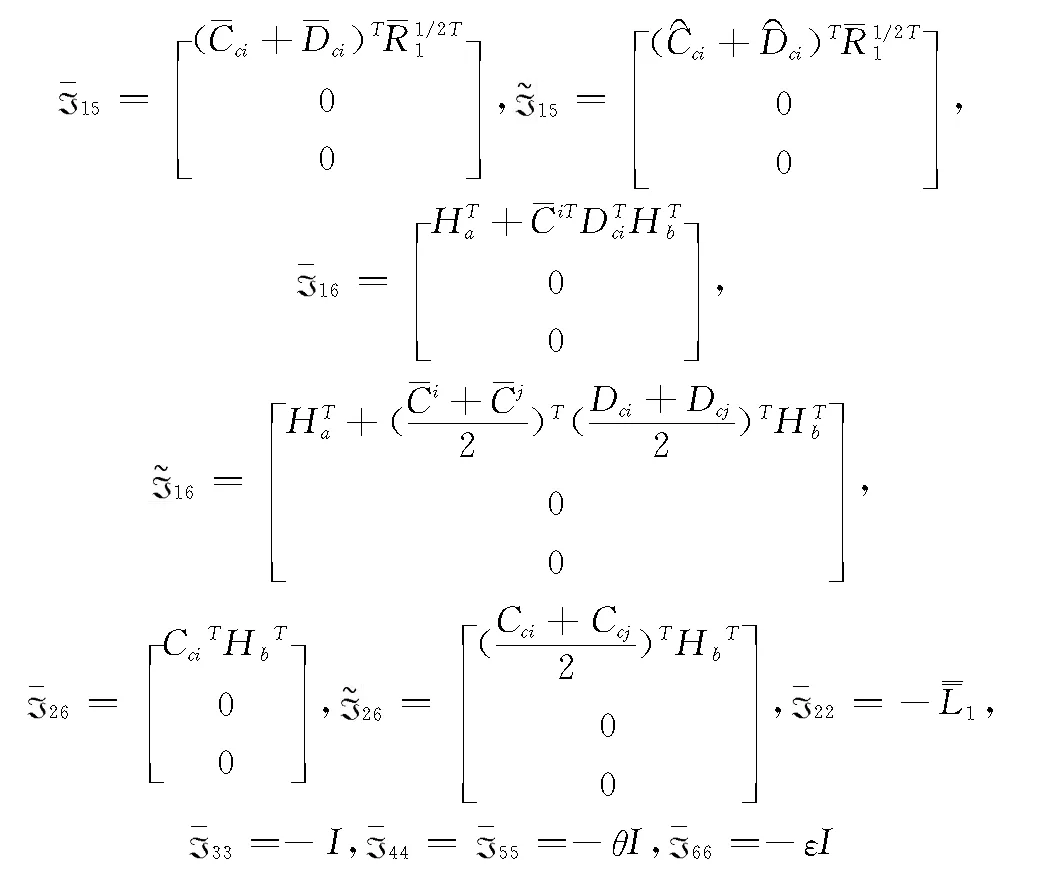
则可以保证非线性闭环系统(15)中的每个子系统渐近稳定，并且根据求解出的参数可以获得对应的控制律。其中，*为关于主对角线对称的元素的转置。式中，

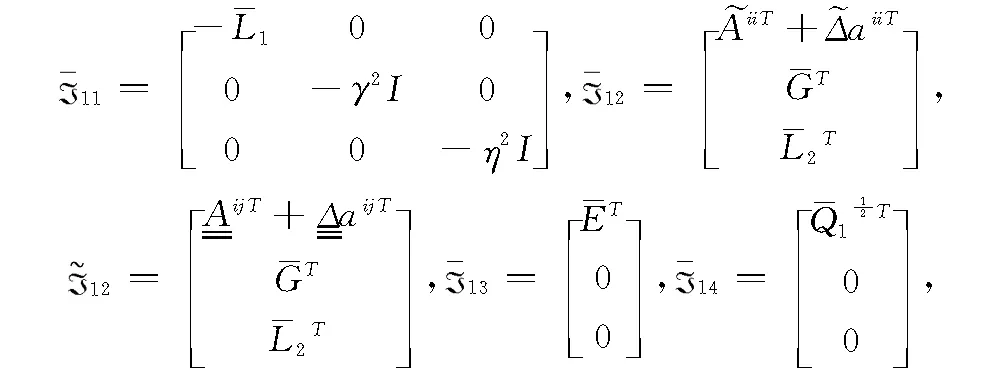
η2ΔrT(k+1)Δr(k+1)]

(34)

(35)

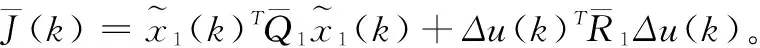
在定理1证明的基础上，结合式(30)，可得：

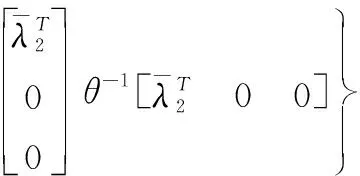
(36)

根据定理1的证明和式(28a)、(28b)，可得:

(37)

在此基础上，分别考虑子模型与子控制器的对照关系，利用引理1则可以得到式(33a)和式(33b)。定理2证毕。

注释5：在同时考虑到设定值变化和外界干扰对系统影响时，可以有两种处理手段。一种是将外界干扰和设定值的变化量看作一个整体的范围较大的有界干扰，通过在鲁棒预测性能指标的基础上引入一个H无穷性能指标，从而降低控制系统对这个范围较大的有界干扰对系统的影响，实现对外界干扰和设定值变化的处理能力。第二种方式是将设定值的变化量和外界干扰分别看作两个独立的有界干扰，通过分别设计H无穷性能指标，分别实现控制器对外界干扰和设定值变化量的有效控制。因为第二种方法为分别考虑设定值变化量和外界干扰对系统的影响，并没有将两者看作一个范围较大的有界干扰，从而实现降低保守性的目的，因此，在定理2中，选择第二种方法进行控制器设计。

3 仿真研究

为了验证提出方法的可行性，根据所建立的啤酒发酵罐温度系统模型分别对定理1和定理2进行仿真验证，并将定理2与文献[21]中提到的方法进行对比，来验证系统快速跟踪变化设定值的能力。

3.1 定理1仿真结果

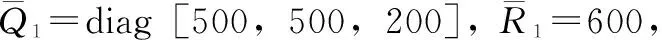
图2 采用定理1方法仿真验证的输出响应曲线

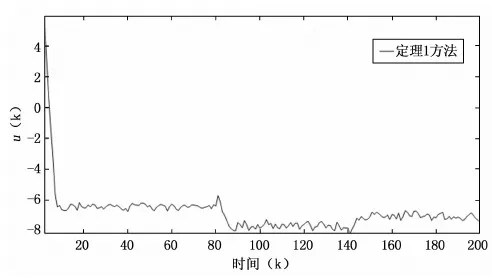
图3 采用定理1方法仿真验证的控制输入曲线

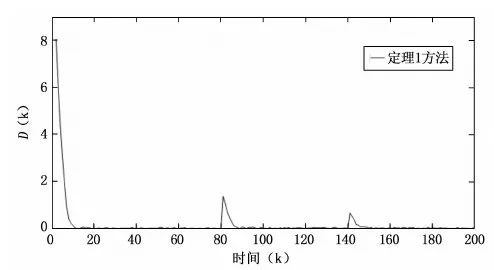
图4 采用定理1方法仿真验证的跟踪性能曲线

由图2可知，提出的输出反馈方法在啤酒发酵罐温度系统在受到不确定性影响时，可以保证系统稳定运行的同时增加系统跟踪设定值的能力。由于在设计控制器时充分考虑到设定值变化对系统输出的影响，将设定值变化的增量看作外界有界干扰，并基于此引入H无穷性能指标增加系统抗设定值变化的能力。因此，当设定值发生变化时，在提出方法的作用下，系统输出也能快速地跟踪期望的设定值，并随着设定值的波动有效变化，满足由于生产工艺需要对温度变化的控制要求，曲线波动也较平缓，因此可以看出采用定理1设计的控制器可以对啤酒发酵过程温度控制系统实现有效的控制。

因为设计控制器时，采用鲁棒模型预测控制思想，通过引入鲁棒预测性能指标，将控制目标转化为无穷时域的优化问题，所以所设计的控制器具有预测控制的预测特性，正是预测特性的存在，使得在被控对象的输出在跟踪上设定值的同时，控制输入具有较小的波动。由图3可以看出，当存在不确定性因素时，虽然在设定值改变时出现较大的变化，但当系统跟踪上设定值后，系统控制输入的波动幅度较小。这种情况一方面降低了执行器运行时的能源消耗，另一方面避免了执行器大范围频繁波动造成的损耗，从而增加执行器的使用寿命，降低了企业的生产成本。

众所周知，基于状态空间模型设计的控制器，通常只是保证系统稳定，也就是使系统的状态输出趋于0，并不能使得系统输出跟踪目标的设定值，大大降低了控制器在实际生产中应用的可能。而提出方法在设计控制器时充分考虑到实际生产需要使系统输出跟踪目标设定值的情况。在传统状态空间模型中引入输出跟踪误差作为扩展状态，使得设计的控制器具有同时调节系统状态和输出跟踪误差的能力。也就是说将输出跟踪误差作为一个新的状态变量，控制器通过将新的状态变量输出控制为0，从而保证被控对象的输出具有良好的跟踪设定值变化的能力。因此，由图4可知，定理1中给出的方法在控制系统受到不确定性影响的情况下，保证系统具有良好的跟踪性能，从而使啤酒发酵罐的温度有效跟踪酵母菌活性最佳的温度，提高企业的生产效率。

3.2 定理2对比仿真结果

为了验证定理2的可行性，在定理1仿真控制器参数的基础上，增加外界干扰对系统的影响，并与文献[21]中提到的方法进行对比来验证提出方法的优势。两种方法的控制效果对比曲线分别如图5～7所示，其中图5为输出响应对比，图6为控制输入对比，图7为跟踪性能对比。

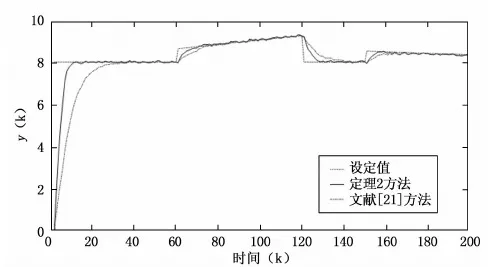
图5 两种方法输出响应对比

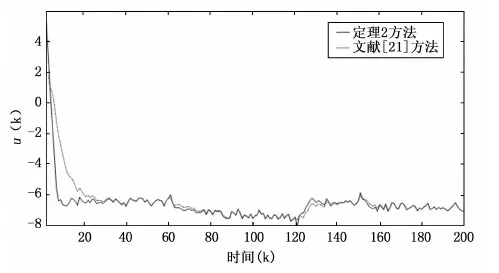
图6 两种方法控制输入对比

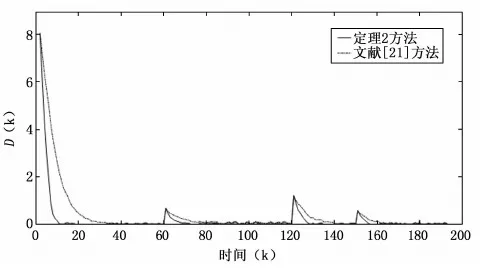
图7 两种方法跟踪性能对比

由图5可知，在相同的影响因素情况下，由于提出方法增加了控制器在设定值变化情况下的调节能力，因此无论设定值是跳变增大或减少，还是慢速均匀增大或减小，提出方法输出响应跟踪设定值的速度都要优于对比文献方法。产生这种效果的原因在于，在设计控制器前充分考虑到实际生产中，控制系统的设定值会随着生产条件的变化发生改变的情况。通过将设定值变化的增量与H无穷性能指标相结合，构建包括设定值变化和外界干扰的复合性能指标。因为在性能指标中并没有将设定值变化和外界干扰看作整体干扰，而是分别构建H无穷性能指标，降低控制器设计中保守性的同时增加了控制器对外界干扰和变化设定值的处理能力。因此，在系统稳定时增加外界干扰，定理2方法和文献[21]方法都能保证系统输出具有较小波动的情况下跟踪设定值。但当设定值根据生产要求发生变化时，定理2方法对设定值变化的影响更加灵敏，具有更强的跟踪设定值变化的能力。

因为定理2中控制器设计时构建的性能指标比文献[21]多了对变化设定值的处理能力，因此，求解出的控制量会有更加快速的调节，从而保证系统输出快速跟踪变化的设定值。由图6可知，在设定值变化的情况下，提出方法的控制输入反应更加灵敏，意味着提出方法可以在较短时间内对执行器进行有效操作，从而达到理想的控制效果。

由于定理2控制器设计时使用了扩展输出误差的新型多自由度状态空间模型，并在性能指标选择中使用了包括设定值变化量的性能指标。因此，定理2中设计的控制器比文献[21]中设计的控制器在保证系统输出跟踪设定值能力的同时具有较强的跟踪变化设定值的能力。由图7可知，定理2给出的方法会大大提高啤酒发酵罐温度控制系统跟踪设定值的速度，尤其是在设定值发生跳变的情况下。这说明提出的方法具有较强的跟踪设定值能力。

两种方法的误差平均值与方差如表1所示。由表可以看出，提出方法的误差平均值与方差均小于对比文献方法，从而体现出提出方法的优势。

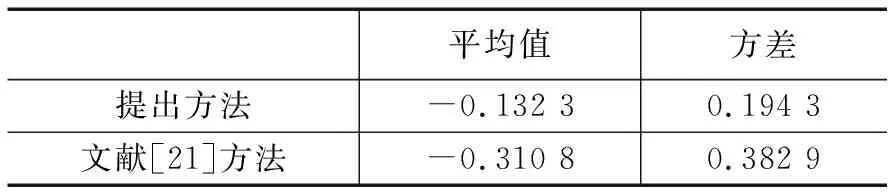
表1 两种方法误差数据对比

4 结束语

本文针对啤酒发酵罐稳定控制系统在考虑系统的非线性特性、参数不确定性和外界未知干扰的情况下，结合实际生产中状态不可测以及设定值会随着生产要求进行调整的情况，提出一种动态输出反馈鲁棒模糊预测控制方法。该方法给出了构造非线性输出反馈控制器的方法以及需要满足的充分条件，有效地降低了由于单点线性化造成的模型不匹配问题的影响，并在系统受到干扰和设定值变化的情况，引入性能指标，保证系统对时变轨迹的跟踪能力，实现被控变量的高精度控制。对啤酒生产工业的发展具有重要意义。