非同轴两轮机器人自平衡与转向闭环控制

周鑫强,石晓辉,黄剑鸣

(重庆理工大学 车辆工程学院，重庆 400054)

0 引言

随着自动控制理论和传感器技术发展，两轮机器人作为近几年发展起来的新型移动机器人具有运动灵活、能源清洁、结构简单等特点[1]，在安保巡逻、快递运输、灾区救援等领域具有广阔运用前景[2]，因此受到国内外众多学者研究[3-8]。

非同轴两轮机器人结构类似于自行车，在侧向方向上是不具有直接驱动的，属于典型的欠驱动非完整约束系统[9]，在正常情况下车身是不平衡的容易倾倒。保持车身平衡就是自平衡控制问题，同时也是非同轴两轮机器人转向闭环控制的前提。

目前对于非同轴两轮机器人基于前轮转角来实现自平衡控制方面研究已经取得了许多成果。例如文献[10]中利用动量矩定理建立了自行车动力学模型，设计了变增益LQR(linear quadratic regulator，线性二次调节器)自平衡控制器，实现了自行车直线变速行驶；文献[11]中利用拉格朗日方程建立了自行车动力学模型，针对车身侧倾角和车身侧倾角速度分别设计了PID(proportion integration differentiation，比例、积分、微分)控制器，利用双PID切换控制实现了无人自行车的匀速直线运动；文献[12]中建立了无人自行车在直线行驶自平衡和90°车把定车运动状态下的动力学方程，利用泰勒级数法进行线性化，针对两种运动状态设计了自适应模糊控制器；文献[13]在匀速圆周和匀速直线运动状态下分别设计了相应的模糊PID控制器，并借助车身倾角和车把转角双位置环控制器，改善了系统的动态响应。文献[14]中分析了轴距、自行车质心、前叉倾角对无人自行车系统稳定性影响，提出速度修正函数与最优控制相结合的全状态反馈自平衡控制。

上述文献中，针对无人自行车动力学模型中非线性时变的不确定部分采用模型线性化方法来处理，而该方法的理想条件是无人自行车处于低速、车身侧倾角和前轮转角较小工况。因此设计的自平衡控制器只有在该工况下具有较好的控制效果，为无人自行车自平衡控制提供了一定的研究思路和基础。但是还是存在以下几点问题：其一，没有考虑到无人自行车在车速、车身侧倾角和前轮转角变化较大工况下不满足动力学模型线性化处理的理想条件时，模型线性化处理对于无人自行车动力学模型准确性和自平衡控制器控制效果产生的影响；其二，当无人自行车侧向方向上遭受干扰时，自平衡控制器使无人自行车车身恢复平衡所需的时间较长，往往需要花费数秒钟，因此需要提高自平衡控制器的响应速度，从而缩短车身稳定时间；其三，没有进一步研究当前轮转角作为自平衡控制器的控制量时，如何实现无人自行车的转向闭环控制，只是停留在直线行驶和开环转向阶段，当无人自行车面临复杂路面情况时无法投入使用。

针对上述问题，文中利用动量矩定理法建立了非同轴两轮机器人动力学模型，在车速、车身侧倾角和前轮转角变化较大工况下，基于建立的动力学模型设计了一种响应快、超调低和鲁棒性较强的RBF(radial basis function，径向基函数)神经网络模糊滑模自平衡控制器，利用RBF神经网络能够自适应逼近非线性函数特性[15]，对动力学模型中非线性时变的未知部分进行自适应逼近，从而避免了由于模型线性化处理方法对动力学模型准确性和自平衡控制器控制效果带来的影响。随后建立了非同轴两轮机器人在大地坐标上的运动学方程，在得到的运动方程基础上建立了基于纯跟踪法的轨迹跟踪控制器，设计利用非同轴两轮机器人车身平衡时车身侧倾角与前轮转角的关系，将闭环转向控制中所需的目标前轮转角替换为目标车身侧倾角，从而将轨迹跟踪控制器与自平衡控制器结合起来，实现非同轴两轮机器人带有轨迹跟踪的转向闭环控制。

1 非同轴两轮机器人动力学模型

针对非同轴两轮机器人这类欠驱动、非线性系统，文中选择动量矩定理法建立非同轴两轮机器人的动力学模型。

如图1和图2所示，非同轴两轮机器人主要由前轮、车体、后轮三部分组成。其中W为整车质心位置；P1P2分别为前后轮与地面接触点；h为质心高度；l为轴距；b为质心至后轴距离；δ为前轮转角；φ为车身侧倾角；ψ为偏航角；m为整车质量；v为车速；J为非同轴两轮机器人系统相对于接触线的转动惯量；Q点为速度瞬心。

图1 非同轴两轮机器人结构示意图

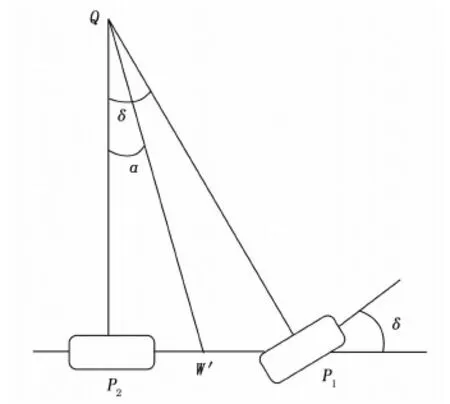
图2 非同轴两轮机器人俯视示意图

根据质点系相对于动轴的动量矩定理[16]，质点系相对于动轴的动量矩对时间的导数等于外力系对动轴的主矩与加在质心上的牵引惯性力的合力对动轴之矩的矢量和。非同轴两轮机器人系统在平面运动时的角速度和角加速度分别为：

(1)

(2)

式中,ω为角速度；ε为角加速度。

则质心投影点W′绕速度瞬心Q转动的速度为：

(3)

式中,rQW′为质心投影点W′至速度瞬心点Q之间的距离；α为非同轴两轮机器人俯视示意图中QW′与QP2间的夹角。

则质心投影点W′处的切向加速度αt和法向加速度αn分别为：

(4)

(5)

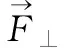
(5)

又因为非同轴两轮机器人所受外力中的前后轮摩擦力在接触线上不产生力矩作用，只有本身重力产生力矩，由动量矩定理可以得以下方程：

(6)

(7)

为了满足后文验证动力学模型线性化处理方法在车速、车身侧倾角和前轮转角变化较大条件下对模型准确性和自平衡控制效果影响的需要，所以对得到的动力学方程中非线性时变的不确定部分进行线性化处理。假设非同轴两轮机器人车身侧倾角φ和前轮转角δ均在较小范围内变动，则sinφ≈φ,cosφ=1,sinδ=δ,cosδ=1得线性动力学方程：

(8)

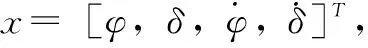
(9)

式中,

表1 非同轴两轮机器人结构参数

2 非同轴两轮机器人运动学模型

如图3所示，为非同轴两轮机器人在大地坐标上的运动示意图。其中δ为前轮转角；ψ为偏航角；l为轴距；Q点为速度瞬心；RF,RB分别为速度瞬心至前后轮距离；v为车速。

图3 非同轴两轮机器人运动示意图

假设单位时间dt内，非同轴两轮机器人经过的距离为ds，偏航角度变化为dψ，则根据几何关系有：

(11)

而RB=l/tanδ,所以由上式可得：

(12)

此外结合非同轴两轮机器人在大地坐标系上的速度为(vx,vy)=(vcosψ,vsinψ),得到非同轴两轮机器人在大地坐标上的运动学方程为：

(13)

3 非同轴两轮机器人控制器设计

图4 非同轴两轮机器人系统整体控制框图

3.1 自平衡控制器设计

RBF神经网络模糊滑模控制思想是利用RBF神经网络逼近特性，对滑模控制律中包含的动力学模型中不确定性函数进行逼近，将逼近后得到的新函数代替原有的不确定性函数，并结合模糊控制思想[17]对指数趋近律中的等速趋近项参数进行模糊控制，以此来削弱系统抖振。

从滑模控制的定义可知[18]，一个滑模控制器的设计主要包括滑模面函数和控制律设计。

3.1.1 滑模面函数设计

为了跟踪轨迹跟踪控制器传递来的期望车身侧倾角，从而实现车身平衡，所以滑模面函数设计如下：

(14)

(15)

e=φd-φ

(16)

(17)

(18)

式中,e为跟踪误差；φd为期望车身侧倾角；c为模糊滑模控制算法控制参数。

3.1.2 滑模控制律设计

(19)

式中,

则式(15)变为：

(20)

趋近律选择指数趋近律：

(21)

式中,n,k为模糊滑模控制算法参数。

由式(20)～(21)得控制律u为：

(22)

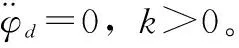
在控制律式(22)中包含的函数f与非同轴两轮机器人质心高度h、车速v、轴距l、前轮转角δ和车身侧倾角φ参数有关，所以在非同轴两轮机器人行驶过程中会发生改变是非线性时变的不确定性函数。利用RBF神经网络对其逼近，可以消除其不确定性对自平衡控制产生的影响。

3.1.3 RBF神经网络设计

RBF神经网络初始结构取2-5-1，即输入个数为2，隐含层神经元个数为5，输出个数为1,输入输出算法为：

(23)

f(x)=W*Th(x)+ε

(24)

式中,x为网络输入；f(x)为网络输出;i表示网络输入层第i个输入，j为网络隐含层第j个网络输入；h=[hj]T为高斯基函数的输出；W*为理想网络权值；ε为网络逼近误差，ε≤εn；cj和bj分别为高斯函数中心点坐标和宽度参数。

(25)

(26)

由新的控制律式(26)、式(20)和式(24)得：

(27)

其中：

设计Lyapunov函数为：

(28)

式中,γ为模糊滑模控制算法参数，γ>0。

则由式(26)～(28)得：

(29)

取自适应律为：

(30)

则式(29)变为：

(31)

3.1.4 模糊规则设计

在得到的新控制律式(26)中，由于采用了指数趋近律，使得系统抖振较大。为了保证系统快速趋近切换面s=0，同时削弱系统抖振，可以对指数趋近律中的等速趋近项参数n进行模糊控制。根据专家经验模糊规则应该设计如下：

图5 输入量的隶属度函数曲线

图6 输出量隶属度函数曲线

3.2 轨迹跟踪控制器设计

针对轨迹跟踪算法有纯跟踪法[19]、MPC(model predictive control，模型预测控制)法[20]、LQR[21]法等，本文选择纯跟踪法作为路径跟踪方法。纯跟踪法的基本思想是以车辆后轮作为中心位置，然后根据预瞄距离ld在参考轨迹上寻找预瞄点C，假设车辆后轮以转弯半径为R到达预瞄点，根据预瞄距离ld、转弯半径R、预瞄点与中心位置偏角θ就可以确定前轮转角δ，纯跟踪法原理如图7所示。

图7 纯跟踪法原理图

为了使非同轴两轮机器人沿者半径为R的轨迹到达参考路径上的预瞄点C，在ΔOCP2中需满足以下关系：

(32)

化简得到：

(33)

根据阿克曼转向关系得到：

(34)

所以从式(33)和式(34)得到：

(35)

从式(35)可以看出纯跟踪法计算得到的是目标前轮转角δd，而前文自平衡控制器输入是目标车身侧倾角φd，所以不能直接作为自平衡控制器输入。而根据非线性动力学方程式(8)可以看出，当非同轴两轮机器人车身平衡后，车身侧倾角φ和前轮转角δ是具有耦合关系的，根据耦合关系可以将目标前轮转角δd转换为目标车身侧倾角φd，耦合关系如下：

-gltanφd=v2tanδd

(36)

4 仿真实验和分析

利用MATLAB/Simulink搭建的非同轴两轮机器人仿真系统如图8所示。

图8 MATLAB/Simulink仿真系统

图8中期望轨迹模块内部存放的是期望轨迹的(x,y)坐标；其余轨迹跟踪控制器模块、自平衡控制器模块、角度转换模块、运动学模块、动力学模块的输入输出参数和功能已经在第3节中进行了详细介绍。

模型准确性实验和自平衡实验步骤如下。

步骤1：只保留自平衡控制器模块和动力学模块，隔离有关轨迹跟踪功能模块，期望车身侧倾角φd设置为0度，使得非同轴两轮机器人仅具有自平衡功能。

步骤2：根据实验中所需的工况，按照表2分别配置动力学模型中初始车身侧倾角φ0、初始前轮转角δ0、车速v。

步骤3：首先对自平衡控制器中RBF神经网络参数bj和cj进行训练优化，再对模糊滑模控制算法参数c,k,γ,n进行优化，保证自平衡控制器具有良好的控制效果。

步骤4：进行仿真实验，获取所需的实验数据，对实验数据进行分析总结。

轨迹跟踪实验步骤如下。

步骤1：导入之前实验中隔离的有关轨迹跟踪功能模块。

步骤2：根据轨迹跟踪实验所需的工况，按照表2分别配置动力学模型中初始车身侧倾角φ0、初始前轮转角δ0、车速v。

步骤3：对轨迹跟踪控制器中的参数前视距离ld进行优化，保证轨迹跟踪控制器具有良好跟踪能力。

步骤4：进行仿真实验，获取所需的实验数据，对实验数据进行分析总结。

仿真实验之前，对前文线性化处理后得到的线性动力学方程式(9)分别设计了基于经典滑模控制算法的自平衡控制器和基于纯跟踪算法的轨迹跟踪控制器，与本文对非线性动力学方程式(8)设计的RBF神经网络模糊滑模自平衡控制器和纯跟踪法轨迹跟踪控制器进行对比实验。实验中工况类型见表2，自平衡控制器中模糊滑模控制算法参数优化结果为c=50,k=20,n=10,γ=20。

表2 工况种类

4.1 RBF神经网络参数cj和bj训练优化

图9 均方差与隐含层神经元个数关系曲线

图10 训练样本和测试样本曲线

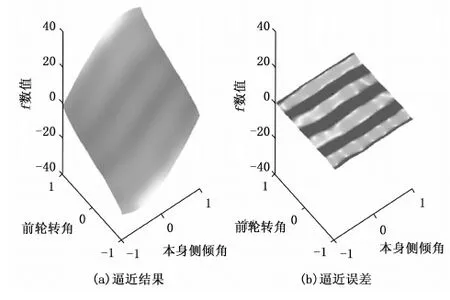
图11 逼近结果和逼近误差曲线

从图9中可以看出，隐含层神经元个数为300个时，此时均方差为0.348 8，当隐含层神经元个数继续增加1 000个时，均方差仅下降了0.033。由于隐含层神经元个数增加不仅会使得网络结构变复杂，还会增加网络逼近所需的时间，所以为了加快RBF神经网络逼近速度，同时保证良好的逼近效果，将隐含层神经元个数设置为300。训练优化后的RBF神经网络结构变为2-300-1，参数bj=0.65，矩阵cj列大小与隐含层神经元个数有关变为2行300列大小的矩阵。从图11中可以看出，利用训练优化好后的RBF神经网络对测试样本逼近具有良好的效果，误差分布在[-1,1]之间。

4.2 模型准确性实验分析

为了验证在面对车速、车身侧倾角和前轮转角变化较大情况下，本文提出的利用RBF神经网络对非线性动力学模型式(19)中非线性时变不确定函数f逼近造成的模型误差，在表2所示3种工况下进行模型准确性实验，实验结果如下所示。其中图12为两种处理非线性时变不确定函数f方法造成的模型误差曲线；表3为模型误差实验数据，表中模型误差收敛时间是指模型误差曲线进入[-1,1]范围内时所需的时间。

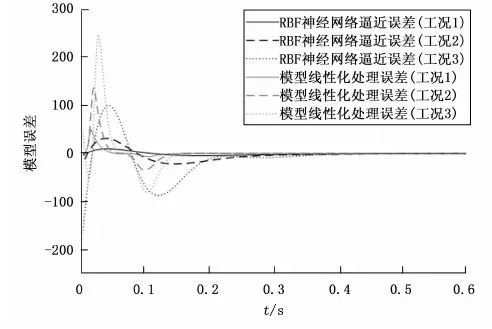
图12 两种处理方法造成的模型误差曲线

表3 两种处理方法的模型误差实验数据

从图12中可以看出，在3种工况下非同轴两轮机器人车身平衡后两种处理方法造成的模型误差都能收敛到0附近，这是因为此时期望车身侧倾角φd和期望前轮转角δd都设置为0度，即非同轴两轮机器人做直线行驶，使得非线性时变不确定函数f最终值为0。只有当期望车身侧倾角φd和期望前轮转角δd都不为0度时，即非同轴两轮机器人做连续转向运动，此时模型线性化处理方法不满足理想条件，造成的模型误差会以一个非0值一直存在。而RBF神经网络利用其逼近特性，造成的模型误差会尽可能收敛到0。

虽然模型误差能否收敛到0对自平衡控制器控制效果具有影响，但是影响的主要因素是模型误差能否在短时间内快速、平稳的收敛到0。从表3中数据可以看出，RBF神经网络逼近方法产生的模型最大误差与模型线性化处理方法产生的模型最大误差相比：在工况1下，从49.90下降至9.55，减少了40.35；在工况2下，从136.90下降至31.50，减少了105.40；在工况3下，从246.30下降至99.82，减少了146.48。因此在面对车速、车身侧倾角和前轮转角变化较大情况下，RBF神经网络逼近方法能够有效的减小模型最大误差，从而提高了动力学模型的准确性，更有利于后续的自平衡控制。虽然所需的模型误差收敛时间相较于模型线性化处理方法虽然增加了0.26 s、0.28 s和0.29 s，但仍处于可接受范围。

4.3 自平衡实验分析

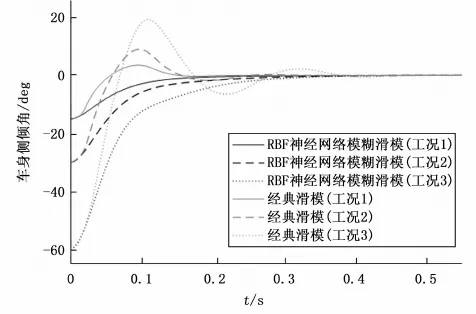
图13 自平衡实验车身侧倾角响应曲线

为了验证在面对车速、车身侧倾角和前轮转角变化较大情况下，本文设计的RBF神经网络模糊滑模自平衡控制器控制效果好坏，在表2所示3种工况下进行自平衡实验，实验结果如下所示。其中图13和图14分别为实验过程中车身侧倾角响应曲线和前轮转角响应曲线，其中车身平衡后车身侧倾角和前轮转角都应在0 deg附近；表4为车身侧倾角实验数据，其中车身平衡所需时间是指车身侧倾角曲线收敛到[-1,1]deg范围内所需的时间。

图14 自平衡实验前轮转角响应曲线

表4 车身侧倾角实验数据

结合图13和表4可以看出，RBF神经网络模糊滑模自平衡控制器与经典滑模自平衡控制器相比：在工况1下，车身侧倾角曲线超调量下降了约3.54 deg，车身平衡时间增加了0.02 s；在工况2下，车身侧倾角曲线超调量下降了约9.04 deg，车身平衡时间增加了0.09 s；在工况3下，车身侧倾角曲线超调量下降了约19.19 deg，车身平衡时间增加了0.12 s。该结果与动力学模型准确性有关：因为RBF神经网络处理方法能够有效的减小模型最大误差，所以使得车身侧倾角曲线超调量能够有效的下降至0 deg附近；又因为RBF神经网络处理方法所需的模型误差收敛时间增加，所以使得车身平衡所需时间也相应增加。因此在车速、初始车身侧倾角和初始前轮转角快速增大情况下，RBF神经网络模糊滑模自平衡控制器与经典滑模自平衡控制器相比，具有更低的超调量和更好的鲁棒性，虽然车身平衡所需时间增加了，但是也远低于文献[8-12]中的自平衡控制器。

此外从图15中还可以看出在3种工况下,经典滑模自平衡控制器的前轮转角波动幅度为[-59.5,76.8]deg，RBF神经网络模糊滑模自平衡控制器的前轮转角波动幅度为[-22.5,49.6]deg，明显小于经典滑模自平衡控制器。因此RBF神经网络自平衡控制器使车身平衡所需的前轮转角更小，而前轮转角作为控制量，所以系统能量消耗也更小。并且实际使用中非同轴两轮机器人前轮转角是有限位的，可能无法满足经典滑模自平衡控制器所需前轮转角波动范围的要求。

4.4 轨迹跟踪实验分析

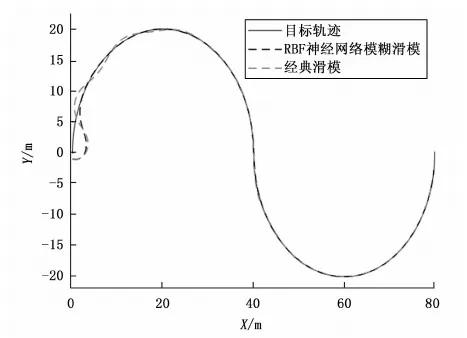
图15 运行轨迹

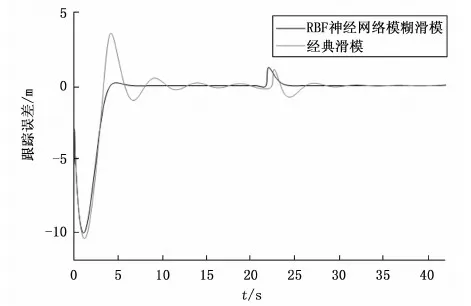
图16 跟踪误差曲线

图17 轨迹跟踪实验车身侧倾角响应曲线

表5 跟踪误差实验数据

从图15～17和表5中可以看出，RBF神经网络自平衡控制器凭借车身侧倾角曲线更低的超调量和更快的收敛速度，能够快速准确的跟踪目标轨迹，其中最大跟踪误差从3.58 m下降至0.19 m，减小了3.39 m；成功跟踪时间从28.80 s下降至5.45 s，减小了23.35 s。此外在24 s左右时，两者的跟踪误差曲线发生波动，是由于非同轴两轮机器人行驶到两个半圆相交处导致目标轨迹方向发生突变，但是RBF神经网络模糊滑模自平衡控制器的跟踪误差曲线波动很快得到抑制。因此利用车身平衡后车身侧倾角与前轮转角耦合关系，将转向闭环控制中所需的目标前轮转向角替换为目标车身侧倾角，使RBF神经网络模糊滑模自平衡控制器与纯跟踪轨迹跟踪控制器相结合，实现带有轨迹跟踪的转向闭环控制是可行的，并且具有良好的轨迹跟踪效果。

5 结束语

1)在非同轴两轮机器人基于前轮转角的自平衡控制中，即使前轮转角作为控制量用于自平衡控制，也可通过车身平衡时的车身侧倾角与前轮转角之间的耦合关系，将转向闭环控制中的目标转向角替换成目标车身侧倾角，将闭环转向控制与自平衡控制结合，从而实现转向闭环控制。

2)对于动力学模型中非线性时变的不确定部分使用模型线性化处理方法，在车速、前轮转角和车身侧倾角变化较大的情况下会产生较大的模型误差。而利用RBF神经网络逼近非线性动力学模型中不确定部分的方法，在上述情况下可以很好的抑制产生的模型误差，使3种工况下的模型最大误差分别下降了40.73、135.14和137.74。

3)模型准确性对于自平衡控制会产生较大影响，并进一步影响到轨迹跟踪控制。主要原因是模型误差曲线超调量和收敛时间增大，会导致自平衡控制中车身侧倾角曲线的超调量和车身稳定所需时间增加，使得自平衡控制效果变差。而自平衡控制效果会影响到轨迹跟踪控制效果，其中车身侧倾角曲线超调量和车身稳定所需时间增加，使得最大跟踪误差和成功跟踪目标轨迹所需时间增大。所以本文设计的自平衡控制器和轨迹跟踪控制器，凭借较高的模型准确性，具有超调量低、鲁棒性强和响应快的优点。