自适应传输技术在风机故障监测中的应用研究
2023-04-03孙思琦崔英英梁雅博张淑洁逯瑞婷
孙思琦,崔英英,梁雅博,张淑洁,逯瑞婷
(1.中国电子科技集团公司 第二十研究所,西安 710061;2.长安大学 信息工程学院,西安 710061)
0 引言
近年来,随着交通运输业的高速发展,隧道交通也在快速发展,目前我国已成为世界上隧道最多、最复杂、发展最快的国家。据交通部和铁道部公布的统计数据,我国现有公路隧道数量达到了21 316处,总长度2 199 km(2020年数据);现有铁路隧道16 798座,总长度19 630 km ( 2020年数据)。随着隧道数量和里程的不断增加,在隧道内发生的火灾也越来越多。有研究人员研究过公路隧道发生火灾的频率,认为公路隧道火灾频率为2次/亿车公里,也即1 000 m长的隧道4~7年有一次火警,2 000 m长的隧道2~3年有一次火警。作为交通道路上的关键线路和控制性节点,长大隧道在给交通运输业做出贡献的同时,隧道内发生的火灾也造成了巨大的社会影响和经济损失。
在隧道火灾防治上,隧道通风子系统做出了极大的贡献。高速公路隧道通风系统负责在隧道日常运作时排出车辆排放的易燃气体以及将新鲜空气送入隧道,因此用于置换气体的轴流风机在隧道通风系统中占据非常重要的地位。由于长期的重载运行以及隧道内外气压差的存在,轴流风机逐渐会出现故障。早期的轴流风机故障通常表现为振动频率的变化且难以察觉,人工巡查无法及时发现故障。目前对于风机等大型旋转机械的健康状况监控能在旋转机械出现明显故障或因故障彻底停工后发出警报,但此时需要投入更多的资金和人力去维修轴流风机。因此对风机的早期机械故障进行诊断,不仅能大大降低风机维护成本,对于防止可控故障发展为重大失控故障、响应国家工业数字化建设有着极其重要的意义。
目前,国内外已有学者开展了基于信号分析的风机故障诊断研究,冷军发等[1]通过FFT分析矿井通风机的振动信号频谱,诊断出其轴系不对中的故障;王卫东[2]采取了对振动信号时域频域结合分析的方法,探查了高炉鼓风机故障类型、部位以及原因;周卓异等[3]通过结合风机噪声信号模型,对轴流风机轴系不对中、转子不平衡、基座松动、叶片损坏4种典型故障的Fourier频谱特征做出了理论分析预测;刘瑶[4]通过深度学习方法,采用长短时记忆模型和残差神经网络两种深度学习方法分别对风机振动信号进行深层特征提取,实现风机故障分类。
迄今为止,国内外学者研究重点可大致分为两类:一类为对轴流风机信号的频域特征进行提取分析;另一类通过对故障诊断过程中的深度学习方法加以改进提升。无论基于哪种方法进行故障诊断,均需要较强的计算能力,在数据采集端直接进行故障诊断受电源和计算能力的限制,因此振动数据需传输到故障诊断专用的上位机。迄今为止的研究未考虑到风机实际工作环境如隧道中振动数据如何发送至故障判别端的问题。在给隧道风机加装故障检测系统的过程中,系统监控到的振动数据需要发送给隧道管理中心,通过有线传输可保证传输带宽,但长大隧道的复杂环境增加了有线传输布线的难度,隧道中无线传输方式多径衰落严重,当传输信噪比恶化时,需要抗干扰能力强的无线传输技术来保证传输的可靠性。
物联网行业的发展掀起了一场通信技术革命,LoRa扩频调制技术作为其产物之一,一直受到广泛关注,LoRa芯片以其抗多径能力强的优点被广泛用于多径衰落严重的信道中。在风机故障监测系统中,振动数据上传的越详细对于系统的故障判别越有利,但在恶劣环境下由于LoRa本身扩频调制的特点,传输信噪比降低时需要增大调制的扩频倍数,因此传输速率受到限制,而轴流风机的故障监测需要实时将振动数据发送到故障判别端。
为了解决这个问题,论文对轴流风机健康状况监测中的数据传输过程进行研究,提出自适应传输机制:将传感器采集到的完整振动数据进行备份,高速公路隧道环境多变,在传输信噪比较高时,LoRa扩频倍数较小,此时LoRa传输带宽充足,上传更加详细的振动数据以提高故障判别的准确率;当信道信噪比降低时,LoRa扩频因子增大使信号的抗干扰能力增强,此时需对振动数据进行选择性上传,通过牺牲小部分细节数据换取故障检测系统的正常运作。当故障判别端检测到异常数据时,则要求发送端重传数据,将完整振动数据发送至故障判别端进行分析。
1 自适应传输机制模型
自适应传输模型如图1所示,加速度传感器将风机振动信号转换为电流信息后送入数据采集卡模块进行处理,采集卡对电流信号进行高频采样并保存至本地存储卡,为了减少数据传输压力,对采样序列进行抽取以及非均匀量化编码。采集卡输出的二进制比特流通过LoRa扩频调制模块,先后经过纠错编码机、交织器和扩频序列产生器,包装为标准LoRa帧结构后由发射天线发送。

图1 自适应传输模型图
隧道中轴流风机的运行时间通常为车流量高峰期,此时隧道车流量大,存在大量噪声,包括了轴流风机自身产生的噪声、汽车发动机噪声以及轮胎噪声等,经测试隧道车辆产生的噪声与以下因素有关。
1)隧道中车辆构成种类:一般来讲,任何车都存在噪声随着行驶速度增大而增大的问题,在同样的行驶速度下,大型车噪声最大;中型车次之;小型车最小。而轴流风机运行时间所在的车流量高峰期,是以大型车的车流量作为标准的。
2)车流量:噪声级随着车流量增加而增加,并且隧道内的噪声高于隧道外的噪声。
3)路面结构:轮胎与路面的摩擦噪声与路面的种类有关,混凝土路面较沥青混凝土路面高2 dB,较碎石路面高4 dB。
4)隧道内墙壁吸声系数:隧道内墙壁对声波的吸收作用小,是造成洞内噪声污染的一个重要原因。
此外,还有车辆鸣笛和路堤高度等因素,可以看出隧道中的噪声成分以及噪声大小是时刻变化且不可控的。因此故障判别端在对接收信号进行解扩恢复后,需要将解扩信号的信噪比实时反馈给发送端LoRa模块。
当信噪比恶化时,LoRa芯片能主动增大调制过程中的扩频因子。目前市面上的LoRa芯片传输带宽均在400~1 000 kHz之间,在传输带宽限制下振动数据的传输速率被降低。若不改变数据采集参数会产生大量振动数据堆积在数据缓存区无法及时发送。而隧道内噪声级做无规律变化增加了人为调整采集卡参数的难度。因此发送端LoRa模块根据信噪比调整扩频因子大小,以调整后的LoRa传输速率作为参考标准,调整抽取因子D与量化编码位数n的大小,减少LoRa待发送数据区的数据缓存,最终使振动数据的传输速率不高于LoRa信息最大传输速率,是自适应传输机制的主要内容。
2 自适应传输关键技术
2.1 基于信号抽取的自适应采样
传感器采集到的振动信号首先需要在采集卡处进行采样。一般情况下,采用周期为TS的冲激函数序列P(t)与待采样模拟序列x(t)相乘的方法,可以实现振动信号的采样过程。该过程如图2所示,采样序列频域上的表现为原频谱X(ω)的多次频谱搬移[7],搬移的角频率为nωs(n=0,±1,±2,…) 。
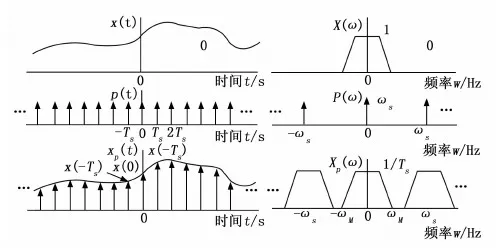
图2 信号的采样过程
其中冲激函数序列的角频率ωs与序列周期TS关系如式(1)所示,TS越小,最终得到的采样序列角频率的搬移越大,发生频谱混叠的概率就越低,对接收端恢复信号越有利。因此在不考虑系统成本和传输功耗时,采样频率越大,对风机故障类型的判别越准确。
(1)
在模拟故障实验中对DTF-5可变翼轴流式通风机的振动信号频域进行分析后发现,轴流风机的故障分为轴承故障、基座松动故障、转子不平衡故障以及定转子碰磨故障。在振动信号频谱低频部分(0~500 Hz),故障工况的频率成分相比于正常工况更加丰富;部分故障工况如轴承故障、定转子碰磨故障等,在高频部分(500 Hz~2.5 kHz)有明显的杂乱频率成分。如图3所示为轴流风机定转子碰磨故障频谱,频率达到2.5 kHz时振动能量基本消失,初采样频率Fs可选择较高的10 kHz用于采集完整的振动数据。为了减轻LoRa传输的压力,采样序列经本地保存备份后,需要进行下采样,即信号的抽取。

图3 定转子碰磨故障
信号抽取是指采样序列每D个采样点只保留下一个,其他采样点数据丢弃的过程,其中D是抽取因子,为整数。信号抽取的本质是采样,因此抽取过程需遵循奈奎斯特采样定理,即Fs/D≥2Fh。
由式(2)可知抽取后信号频谱延拓周期会降低为原来的nωs/D(n=0,±1,±2,…),为防止抽取后频谱混叠程度加剧,采用周期为ωs,宽度为ωs/D的数字滤波器滤掉可能发生混叠的频谱分量。
LoRa在信道环境较好时可上传较多数据,抽取因子D可根据LoRa传输速率进行增减,当噪声增大后,抽取因子D的值开始增加,最终达到Fs/D=2Fh,由于0~500 Hz频段范围内的频率成分可直接判断风机是否出现故障,因此Fh取500 Hz即可。当故障判别端检测到振动信号出现故障分频,立即向接收端发送重传申请,此时发送端会将未经抽取的振动数据发送至故障判别端,从而判断故障的具体种类。
2.2 基于非线性规划的信号量化
信号的量化过程分为均匀量化和非均匀量化,其中均匀量化是指量化区间等间隔划分的量化技术,量化位数n表示量化需要的编码位数,量化间隔Δq与各级量化电平qi的关系如式(2)所示。
Δq=(b-a)/2n
qi=a+iΔq,i=0,1,…,2n
(2)
其中:[a,b]为振动信号幅度的取值范围,均匀量化方法各级量化输出电平值xqi为:
(3)
由于风机故障信号大多表现为小幅度的高次谐波,采用均匀量化不能很好的描述故障信号特征,因此本文采用非均匀量对振动数据进行信源编码。与均匀量化不同的是,非均匀量化的量化间距是基于信号分布估计选择的,量化间隔计算具体步骤如下所示:
1)使用非参数直方图估计法对风机振动信号幅度的分布情况进行估计拟合得到其分布函数。非参数直方图估计法将样本风机振动信号范围划分为M个等距离区间并统计落在每个区间的样本个数,计算每个区间的概率密度后对该直方图进行拟合,最终得到风机振动信号的概率密度函数f(x),轴流风机振动信号拟合曲线如图4所示。

图4 拟合风机振动信号概率密度函数
2)得到量化噪声eq的关系式。 量化噪声eq与信号的概率密度函数f(x)相关,其计算公式为:
(4)
其中:xq为量化输出值,非均匀量化下采样点的量化输出关系如式(5)所示:
(5)
由于信号正负电平的对称关系,即q-(2n-1-1)=-q2n-1-1,非均匀量化的量化噪声可推导为:
(q1-q3)h(q2)+…+(q2n-1-2-q2n-1)h(q2n-1-1)+
(q2n-1+q2n-1-1)h(+∞)]
(6)
在量化噪声eq取最小值的约束下,通过非线性规划函数求出最佳的量化间隔。
通过上方法,无论量化编码位数n的取值为多少,均可得到最优的量化间隔,振动信号经量化编码后进行扩频调制。
3 LoRa扩频调制技术
LoRa 是诸多LPWAN通信技术中的一种, 是一种基于扩频的调制方式,通过扩频把信号扩展到带宽较宽的噪声中,获得扩频增益。香农公式是扩频通信的理论基础,如式(7)所示为单位时间内信道容量、信号带宽和信噪比的关系,其中C为信道支持的最大传输速率或信道容量(b/s);B为信道带宽(Hz);S为平均信号功率(W);N为平均噪声功率(W);S/N为信噪比(dB)。
C=Blog2(1+S/N)
(7)
考虑到限时因素,在一个系统内频带、时间和信噪比三者互换可用公式表示为:
F1T1log2(1+γ1)=F2T2log2(1+γ2)
(8)
其中:F1和F2分别为系统变化前后的频带宽度(Hz);T1和T2为系统变化前的时间(s);γ1和γ2为系统变化前后的信噪比(dB);用频带换取信噪比时扩频通信最常用的方法,根据式(9):
T1=T2
⟹F1log2(1+γ1)=F2log2(1+γ2)
(9)
当λ2≫1时,γ1=γ2F2 /F1,其中F2/F1就是该扩频系统的扩频系数或称为扩频因子。式(9)阐述了在传输信噪比降低时,可通过增大扩频倍数以维持信息最大传输速率或信道容量。
根据扩频的原理,扩频技术可分为直接序列扩频、跳频扩频和线性调频等,其中LoRa芯片采用的线性调频技术通过改变chirp信号扫频的初始频率来表示不同的信息,LoRa信号的带宽为B,码元周期为TS,载波频率为fc,chirp信号可由式(10)来表示。
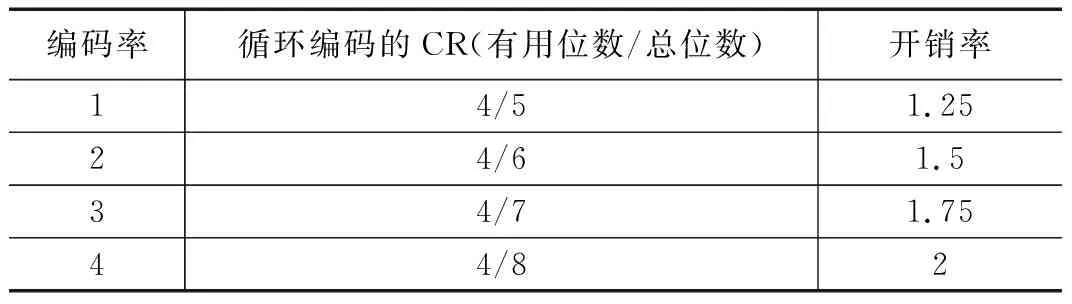
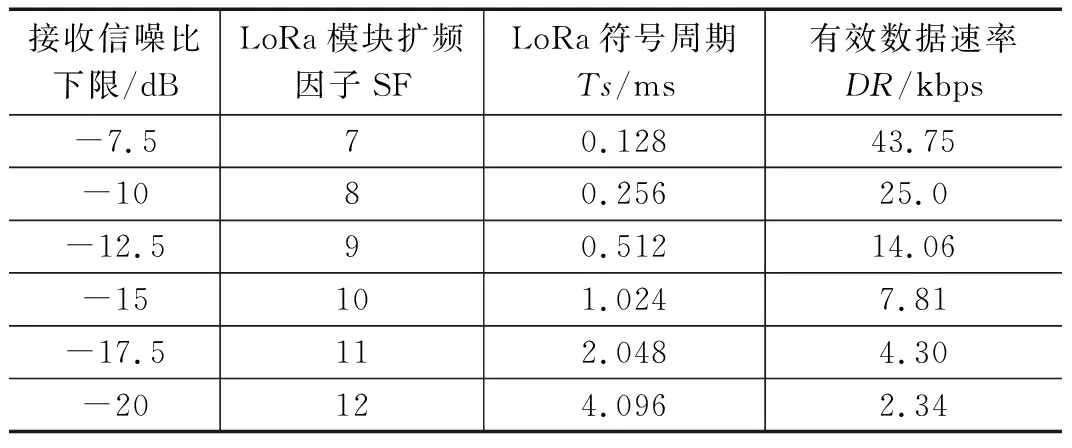
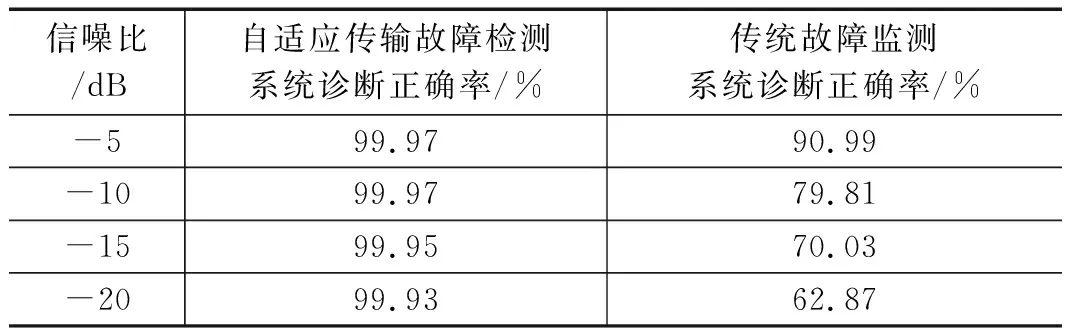
s(t)=ejφ(t)=ej(2πfct+πB/TSt2),-Ts/2 (10) chirp信号的瞬时频率可表示为: (11) 式(11)表明,chirp信号的瞬时频率始终处于线性变化状态。根据扩频因子SF的大小,一个码元符号被扩展为2SF个码片,不同的码片排列顺序可表示2SF个码元符号。即1symbol=2SFchips,每个码片带宽为BW/2SFHz。例如当SF取7时,通过128个码片代表一个码元,系统工作频率为470 MHz,BW=250 kHz,则相邻码片间隔为250 kHz/128=1.95 kHz,其码片带宽如表1所示。 表1 码片带宽表 由表1可以看出,LoRa调制的特点在于不同时间下调制信号的载波频率大小不同,当无线信号在隧道中出现多径传播,经不同路径到达接收端时的时间不同时,在发送端和接收端时钟同步的前提下,接收端有能力过滤掉多径干扰分量,只解调主路径传播过来的信号。 根据码片与信道带宽的对应关系可得出LoRa的码元符号传输时间Ts和符号速率RS与扩频因子的关系如式(12)所示: Ts=2SF/BW Rs=1/Ts=BW/2SF (12) LoRa码元与比特的对应关系为1symbol=SF bit,因此LoRa传输的比特率为: Rb=RS*SF=SF*2SF/BW (13) LoRa调制模块引入了CRC循环冗余校验,纠错编码机将有效载荷数据每4 bit增加1~4位前向纠错编码(forward error correction,FEC),前向纠错编码配置如表2所示,在LoRa中使用的CRC编码率为1。因此LoRa传输的有效数据速率为: (14) 表2 前向纠错编码配置表 针对不同的信道环境,LoRa芯片的扩频因子SF可选范围为7~12,在这里我们选择的LoRa芯片型号为SX1278,其工作频率为410~440 MHz,共计32个信道,单个信道带宽为1 MHz,根据以上公式可得出表3中不同扩频因子下的有效数据传输速率。 表3 SX1278芯片不同扩频因子下传输速率 根据表3中数据,当隧道中环境恶化时,接收端将接收信号的信噪比分析并反馈至LoRa调制发送端,根据不同信噪比下与扩频因子的对应关系,LoRa模块的扩频因子增大至对应的数值,此时有效数据传输速率降低,单位时间内传输的有用数据减少。 本次实验场地为秦岭终南山公路隧道,实验对象为DTF-5可变翼式轴流风机。 系统几何位置图如图5所示,该隧道的轴流风机放置在位于竖井底部的风机机房中,轴流风机通电后,将隧道内的废气排至山顶,并将山顶的新鲜空气源源不断地输送进隧道内,从而达到通风换气的效果。轴流风机上的故障监测系统进行无线传输时,路径最短、耗能最低、传输最高效的路径是沿着竖井进行传输,但是竖井在物理结构上是一条内壁光滑的圆形管道,无线信号在竖井中传输时,会产生严重的多径效应。 图5 系统几何位置图 故障监测系统包括数据采集与处理设备、中继基站、客户端软件。 数据采集与处理设备安装在轴流风机外壳上,包括压电式加速度传感器、数据采集卡、LoRa无线调制模块,负责将轴流风机的振动数据无线发送出去。 由于Lora的传输距离为3~5公里,部分长大隧道长度超过了10公里,隧道风机距管理中心有一定距离,因此设置中继基站安装在竖井出口的信号基站上,用于解决隧道风机与隧道管理所之间的距离超过LoRa最大传输距离的问题。 客户端软件安装在隧道管理所监控中心电脑上,负责将无线传输过来的数据进行故障判别后存储。 图6 终南山隧道风机房 如图6所示为终南山隧道的风机房,在风机房中的轴流风机外壳加装传感器、添加了自适应传输机制的采集卡以及LoRa透传模块,在实验中为了判断风机的故障诊断是否正确,分别通过在叶片根部加载重物实现转子不平衡故障,破坏连接风机叶片与转轴的滚动轴承来模拟轴承故障,将风机地脚螺栓拧松来实现基座松动故障,在风机叶片上粘硬塑料片确保塑料片与风机壳发生摩擦来实现定转子碰磨故障。 由于LoRa模块在不同信噪比下传输速率为定值,采样点数与编码位数在当前传输速率下可有多种取值方式,例如当传输速率为43.75 kbps时,抽取因子和编码位数取2和8或3和12均满足无差错传输的要求,因此在终南山隧道中分别测试不同信噪比时,几种模数转换参数组合下客户端显示数据相对于发送数据的误码率,最终得到在不同传输速率下采样点数与编码位数误码率最低的组合如表4所示。为了方便后续流程图的绘制,为每一种组合增加了序号。 表4 不同信道环境下抽取因子与编码位数组合 根据表4所得结果,自适应传输机制过程可用公式(15)表示,其中符号“┌┐”表示向上取整,“||”表示取绝对值。式(15)描述的流程为:获取接收端反馈的SNR值并进行上取整计算,得到序号i,此时抽取因子D和编码位数n取值为序号i对应的Di与ni。 i=||SNR/2.5||-2,n=ni,D=Di (15) 在转子不平衡、轴承故障、基座松动或定转子碰磨等风机故障已知的条件下,测试不同信道环境下LoRa故障监测系统与普通4G故障监测系统的故障诊断结果,若诊断结果与风机故障类型相同,认为诊断成功,若不相同则认为故障诊断失败,统计并分析故障监测系统诊断错误的概率。 测试结果如表5所示。当信噪比在-5 dB时,信道环境相对较好,Lora可以传输完整的振动数据细节,这对于客户端的故障类型判别是十分有利的;随着信道环境逐渐恶化,振动数据抽取比例增大,由于故障频谱低频部分相似度较大,细节数据的缺失逐渐增加了故障分辨的难度,故障诊断正确率开始降低。 表5 故障监测系统测试结果 由表5可以看出,自适应传输策略使LoRa传输风机振动数据成为可能,普通故障监测系统由于没有LoRa扩频模块强大的抗干扰能力,在数据传输的可靠性方面节节败退,在恶劣环境下丢失大量数据。因此采用自适应传输的Lora故障监测系统能更好的在隧道等恶劣环境下传输数据。 本文提出了基于自适应传输机制的LoRa故障监测系统,传统的故障监测系统无法在隧道等特殊场景下正常工作,因此在原有系统的基础上加装LoRa扩频调制模块,由于LoRa的窄带宽特性,在隧道环境多变的情况下通过自适应传输机制根据信道环境自行调整数据采集参数。在经过多次实验后,相比于在隧道中安装普通的故障监测系统,基于自适应传输机制的LoRa故障监测系统较好的传输性能得到证实,系统的可用性较强。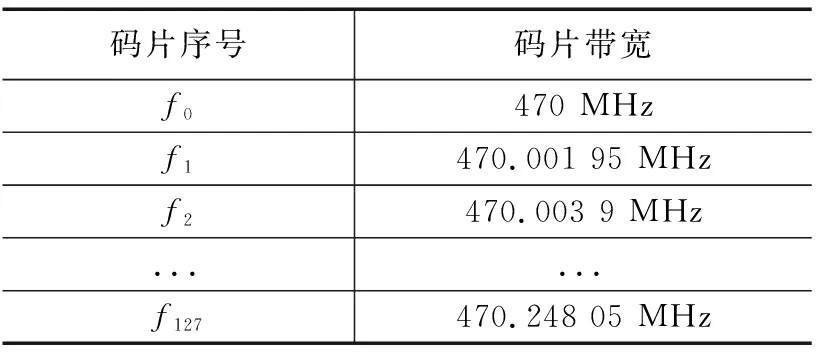
4 自适应传输系统性能测试
4.1 试验场地及系统搭建


4.2 故障监测系统性能测试

5 结束语
