巧构辅助圆，妙解最值问题

齐伟

很多几何问题看似与圆没有任何关系， 但是借助已知条件恰当地构建辅助圆，常常 可以实现问题的转化，让解题思路豁然开朗. 利用辅助圆解答最值问题的关键是根据题 設、结论和图形，巧妙地构造圆，然后再利用 圆的有关性质、结论求解最值问题.

一、由动点定角构造辅助圆求线段最值

最值问题一般体现在动态图形中，至少 存在一个动点，对于动点问题中的定直角条 件，即动点运动过程中，始终有一个角为直 角，我们可以考虑以直角三角形的斜边为直 径构造圆，则直角顶点在圆上，构造出圆后则 可借助圆的性质求最值.把不容易确定的线 段的最小值问题转化为点与圆的位置关系问 题来考虑.

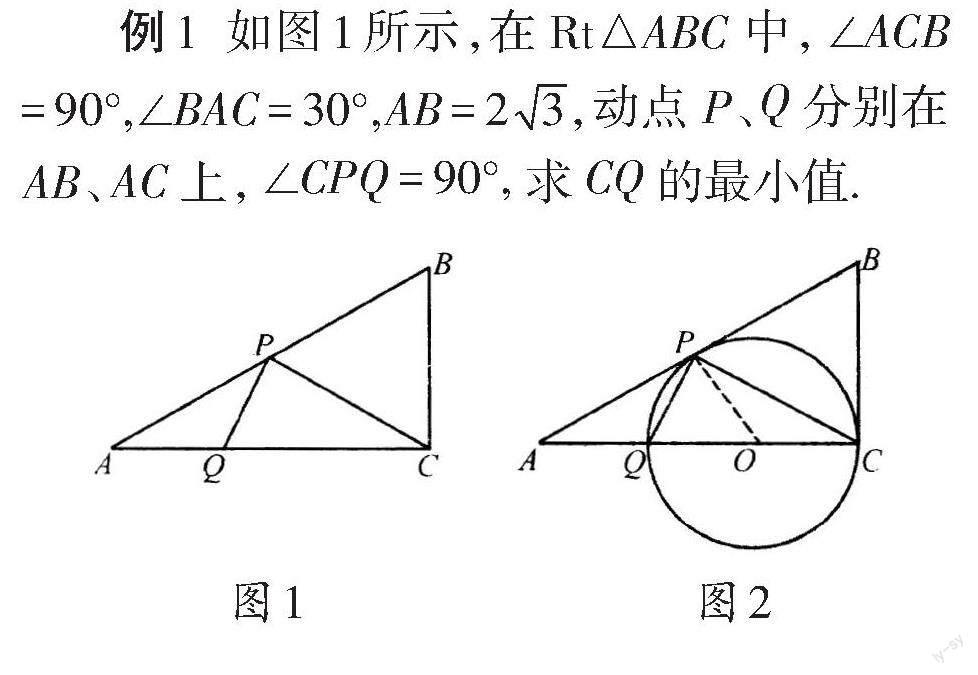
例1

解：

点拨：当题中给出直角时不能单单只想 到勾股定理，也要联想到圆.根据题干条件画 出辅助圆，借助圆的性质：圆心与切线上各点 之间的连线中，圆心与切点之间的线段最短 即可解题.

二、由动点定弦构造辅助圆求角度最值

根据圆周角定理可知：同弧或等弧所对 的圆周角大于该弧所对的圆外角，小于该弧 所对的圆内角.求动点对定线段所张的角的 最大值时，可以添加辅助圆，使定线段为弦， 所张的角为唯一（此时辅助圆与动点所在的 直线或圆相切）的一个圆周角，由同弧所对的 圆周角大于圆外角知，动点运动至切点处时 所张角最大.

例2

解：

点拨：本题考查了垂径定理、圆周角定理 等知识.构造辅助圆，把所张角转化为圆心角 或圆周角，利用圆心角或圆周角确定出动点的运动轨迹，化动为静，对满足条件的动点准 确定位，再解答.

三、由定角定弦构造辅助圆求面积最值

当题目中出现了固定度数的角对着固 定长度的线段时，一般隐含着一个固定大 小的圆，我们以定线段为辅助圆的一条弦， 定角为弦所对的一个圆周角，借助辅助圆 来分析.求面积最值问题首先要从面积公式 入手，将面积问题转化为求三角形高（底） 的问题，再从三角形的高（底）与所隐含的 动圆之间的关系，去发现高（底）取最值时的 状态.

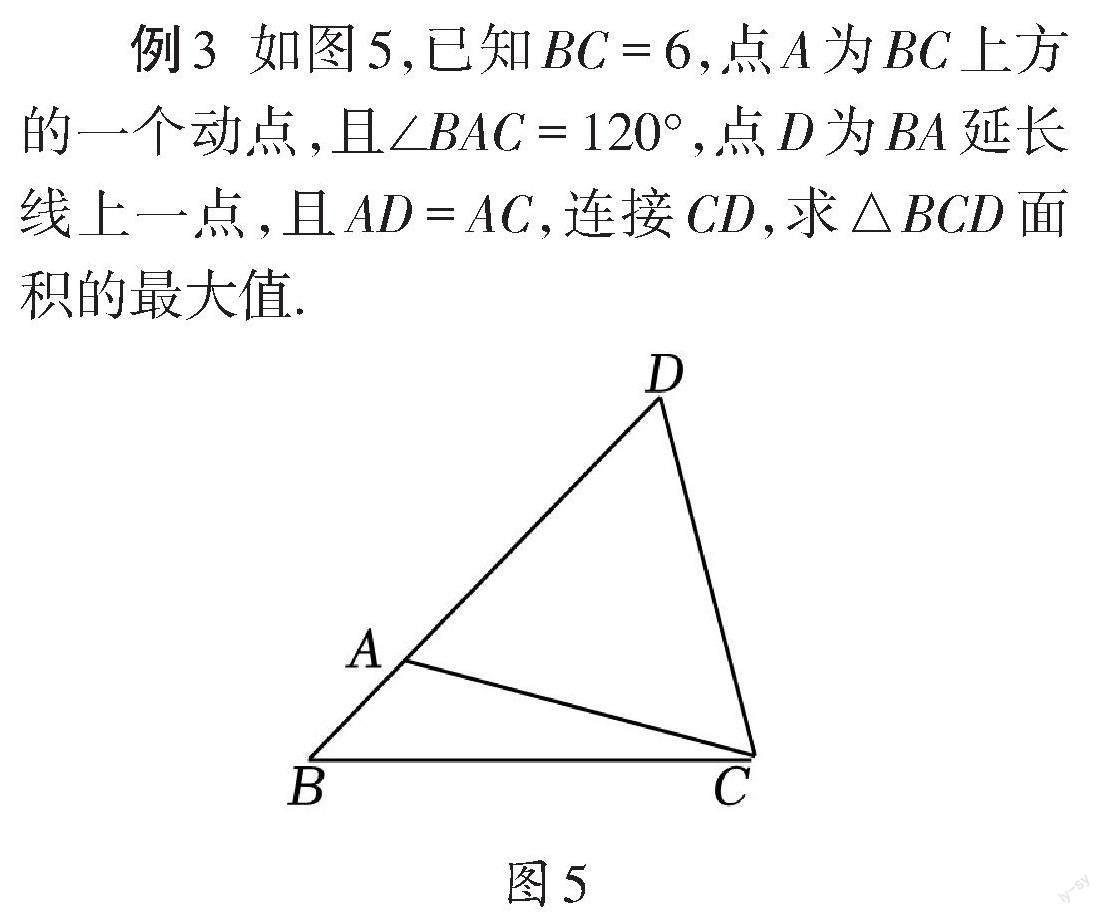
例3

解：

点拨：此题根据定角和定弦的对应关系， 通过添加辅助圆确定最值.决定三角形面积 大小的量是高和底的长，题目中已知底长是 定值，所以要让 △BCD 面积最大，只需让高 EF 最长.利用圆中的垂径定理以及直径是圆 中最长线段即可实现转化.

总之，利用辅助圆的几何特性可以求解 最值问题.解题时要关注其中的几何关系，充 分利用条件提取或构造辅助圆，再结合圆的 性质确定最值情形.同学们在学习过程中，要 关注构建辅助圆的性质定理，深入理解圆中 的几何模型.