多约束超螺旋滑模变结构制导律

周蒙, 钱惟贤, 任侃

(南京理工大学 电子工程与光电技术学院，江苏 南京 210094)

0 引言

在现代战争中，导弹已经得到广泛应用。导弹的任务是在末制导阶段能够以较小的脱靶量精确打击目标；制导律的作用是为导弹自动驾驶仪提供制导指令。一些特殊种类的导弹不仅需要精确打击目标，而且需要以期望的加速度、落点和落角度约束精确命中目标。滑模变结构控制在滑动模态中对干扰具备不变性，对参数变化也不敏感，因此广泛应用在制导律设计中。国内外学者针对以上问题，研究了1 阶滑模变结构制导律、2 阶超螺旋滑模变结构制导律。

传统的1 阶滑模算法主要研究滑模函数和趋近律设计。滑模面包含线性滑模面、终端滑模面、积分滑模面[1]。线性滑模面在距离较远情况下趋近速度较慢，而终端滑模面和积分滑模面的优势可以在距离较近情况下快速收敛至原点。传统的趋近律是基于符号切换函数，但符号函数会引起滑模系统的抖振，目前趋近律多采用饱和函数和双曲正切切换函数设计趋近律[2]。2 阶超螺旋算法相对于1 阶滑模算法具有更高的收敛速度，因此得以广泛应 用[3]。文献[4]设计了一种基于双螺旋算法的2 阶滑模制导律，并基于地空导弹模型进行了算法推导，开展了仿真验证。文献[5]采用双螺旋算法，结合终端滑模控制理论设计了带有攻角约束的2 阶滑模制导律，并通过仿真验证了算法的有效性。文献[6]针对高超声速飞行器，采用超螺旋算法设计了一种自适应2 阶滑模制导律，并利用二次型Lyapunov函数验证了其稳定性，通过仿真实验验证了该算法具有更高的鲁棒性。文献[7]针对拦截高速机动目标时需要满足以指定攻击角命中目标的要求，采用超螺旋算法设计了一种2 阶滑模制导律，仿真结果表明该算法具有较高的拦截性能和鲁棒性。

以上研究所提出的滑模变结构算法并未解决控制受限的问题。控制受限是典型的非线性控制环节，会增加系统的超调、降低控制精度，严重时会引起系统的输出发散[8]，因此控制受限因素有必要考虑。目前，针对控制受限问题，国内外已经出现了一些可以借鉴的成果，例如设计Anti-windup 抗饱和补偿控制器[9-10]、应用Nussbaum 型增益技术[11-12]设计Auxiliary System辅助控制系统[13-16]。

文献[9]针对控制饱和问题，提出了一种基于观测器的新型Anti-windup 抗饱和补偿控制器，通过仿真证明了该控制策略是一种非常有效的方法。文献[10]考虑全状态饱和的无人水面舰艇控制模型，设计一种Anti-windup 抗饱和补偿器，实现了对受限的补偿作用。文献[11]为解决火箭炮位置伺服系统运行过程中所存在不确定非线性因素的影响，采用动态面滤波法，并结合自适应鲁棒控制理论，设计了精确位置控制器，并进行了仿真验证。文献[12]为解决航天器安全接近问题，考虑存在外部扰动和输入受限的情况，并基于滑模控制理论，设计了有限时间收敛的姿态控制器。文献[13]针对具有输入饱和输出受限的纯反馈非线性系统，设计了神经网络自适应控制器，进行了稳定性证明和算法仿真验证。文献[14]引用有限时间收敛理论，结合滑模控制理论，研究了控制受限情况下的制导律设计问题，以动能拦截器拦截临近空间高速机动目标为背景，进行了算法设计和仿真。文献[15]采用罗德里格斯姿态参数，对刚性航天器姿态跟踪动力学进行了描述，考虑模型不确定和输入受限问题，设计了鲁棒自适应状态反馈受限控制器。文献[16]针对无人机姿态控制问题，考虑了控制输入饱和与状态约束的情况，设计了动态辅助系统，控制系统可以在有限时间内稳定，且信号有界。文献[17]为解决欠驱动船控制受限问题，采用动态辅助系统，结合反步法设计中的虚拟控制律，设计了控制算法，并进行了仿真验证。受限辅助系统的主要思想为：在辅助系统设计过程中，将执行机构饱和输出的误差信号反馈到标准控制器中，从而消除输入受限的非线性对系统的影响；在运动过程中，系统如果产生饱和，则会导致辅助系统作用，使饱和量的幅值发生衰减，直到控制量进入线性控制区域，从而辅助系统的输出也随之衰减为零。

本文引用某导弹弹目相对运动模型，并转化为标准2 阶系统模型。基于连续滑模函数设计1 阶滑模制导律，采用双曲正切切换函数代替符号切换函数；基于改进的超螺旋算法设计2 阶超螺旋滑模制导律(STG)；为解决加速度受限带来的非线性问题，设计基于辅助系统的辅助制导律(ASG)，弱化饱和受限带来的影响。理论分析和仿真结果验证了所设计的制导律具有较高的制导精度；ASG 的设计能够有效解决加速度受限的问题。

1 制导模型

将导弹和目标均视为质点，在惯性坐标系Oxy下建立图1 所示弹目相对运动关系。图1 中，q为弹目视线角，v为导弹的运动速度，θ为导弹的弹道倾角，am为导弹的加速度，M为导弹，T为目标。

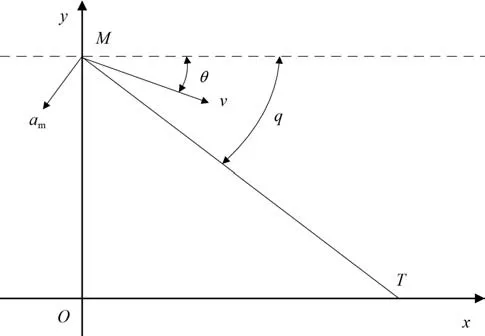
图1 弹目相对运动关系Fig. 1 Relative motion between a guided projectile and a target

设R为弹目相对距离，根据图1 所示的运动关系，可以得到炮弹和目标的运动方程为

将式(1)的第2 个方程两端求导，可得

根据导弹的飞行动力学方程，有

将am作为自动驾驶仪的制导指令，根据 式(2)和式(3)，可得

式中：

式中：umin< 0，umax> 0 为已知常数。

本文研究的导弹打击固定目标，采用卫星和惯性组合导航，算法参数通过卫星和惯性制导的组合导航给出的位置和速度参数，结合目标位置参数，通过坐标关系计算获得导弹和目标在导引坐标系内的视线角和角速度，进而求得导引律在导引周期的值。由于当前卫星和惯性制导的组合导航参数测量值精度高且输出稳定，能够满足导引律和设计指标的要求。

2 滑模制导律设计

本文采用基于趋近律的方法设计1 阶滑模制导律(OSMG)，采用改进的超螺旋算法设计 2 阶OSMG，采用辅助系统理论设计ASG。设计步骤分为三步：

1)根据导弹式(5)弹目相对运动模型，设计线性滑模面，采用基于趋近律的方法设计 1 阶OSMG，并给出Lyapunov 稳定性证明；

2)采用改进的超螺旋算法公式设计基于超螺旋算法的2 阶OSMG，并构造Lyapunov 函数进行稳定性证明；

3)利用制导模型信息，采用辅助系统理论设计ASG，构造Lyapunov 函数证明所设计ASG 的渐进稳定性。

2.1 1 阶OSMG 设计

设期望的弹目视线角为qc，视线角跟踪误差为e=qc-q。设计线性滑模面S1：

式中：c1为正实系数；为视线角跟踪误差1 阶导数。式(7)求导，并将式(4)代入，可得

采用趋近律如下：

式中：µ1、µ2为制导律设计参数，µ1＞0，µ2＞ 0。

根据式(8)和式(9)可得1 阶OSMG

构造如下Lyapunov 函数：

式(11)求导，可得

将式(11)代入式(12)，可得

2.2 2 阶STG 设计

针对导弹标准2 阶系统模型式(5)，选取如下滑模面S2：

式中：c2为设计参数，满足c2＞ 0。将式(14)求导，可得

式(5)代入式(15)，可得

为解决系统固有的抖振，采用饱和函数代替符号切换函数，对文献[19-20]所述的超螺旋算法进行改进，公式如下：

式中：k1、k2为制导律设计参数，满足k1＞ 0，k2＞ 0 。

根据式(16)和式(17)，可得2 阶STG：

针对超螺旋系统的稳定性借助Lyapunov 稳定性定理，需要选择一个矩阵P构造出Lyapunov 函数。当该函数正定且其导数负定时，则说明该系统具备渐进稳定性。

设超螺旋系统的状态变量X为

构建Lyapunov 二次型函数V2：

式中：所选择的矩阵P为

在式(21)中，只要满足k2＞ 0，矩阵P为正定矩阵，Lyapunov 函数V2为正定矩阵的二次型，则说明V2为正定二次型。超螺旋系统设计参数k1、如果满足以下条件[21]：

则可以使Lyapunov 函数的导数负定。所设计的 式(18)2 阶STG 满足Lyapunov 稳定性。进一步说明该超螺旋系统的状态变量X可以在有限时间到达滑模面以及其导数也能在有限时间内收敛至原点。制导律的攻击角度受限问题还有待解决，因此需要进行ASG 的设计。

2.3 考虑加速度受限的制导律设计

参照文献[22-23]中的辅助控制器设计方法，利用式(5)模型信息，设计如下ASG，弱化控制限制对制导律的影响。ASG 状态变量为F，可表示为

由式(23)可知 ASG 的运行分如下两种 情况：

1)滑模变结构制导律运行正常，没有超过限制，式(23)表示的ASG 不作用；

2)滑模变结构制导律超过了约束限制，制导律会生成误差量Δu，则滑模变结构制导律进入超限设定，ASG 运行解算，将滑模变结构制导律限制在设置的限制值范围。

为证明本文所设计的ASG 的稳定性，构造如下的Lyapunov 函数：

根据式(24)可得

将式(23)代入式(25)，可得

综合上述3 种制导律，2 阶STG 收敛速度比 1 阶OSMG 快，2 阶超螺旋滑模控制将传统滑模控制中存在的高频率切换式由W转移到，从而使得高频率的切换项不再影响W，避免了滑模变结构制导律输出信号出现高频率的振荡现象，从而获得更好的制导品质。因此将2 阶STGu2和ASGF结合形成包含多约束的滑模变结构制导律：

设V为表示多约束OSMG 对应系统状态方程的Lyapunov 函数，令V=V2+V3，由于V2和V3的倒数负定，则V的导数也为负定，表示多约束OSMG 对应系统状态方程满足Lyapunov 稳定性。

3 仿真分析

基于式(5)弹目相对运动模型进行 1 阶OSMG、2 阶STG 和ASG 的仿真。设定导弹的飞行速度v为350 m/s，加速度am阈值设为[-5g，5g]，选取初始条件为：导弹飞行高度3 000 m，目标在地面 2 000 m 处，制导律状态变量m，q0=arctan(3/2)×π/180°，初始弹道倾角θ0=-15 °。

为验证2 阶双螺旋算法STG 和ASG 的优势，设置仿真方案如下：方案1，OSMG；方案2，STG；方案3，STG+ASG。

制导律设计参数选取结果如下：

1)OSMG 设计参数：c1=0.1，μ1=10，μ2=5，μ3=2，qc=-80°；

2)STG 设计参数：c2=0.1，k1=4，k2=10；

3)ASG 设计参数：c3=5，be=2，σ=0.1。

本节通过制导算法仿真，结果如下：图2 为导弹加速度；图3 为滑模面误差；图4 为滑模面函数的1 阶导数；图5 为导弹弹道曲线；图6 为导弹的弹道倾角曲线；图7 为视线角速度；图8 为ASG的输入输出变量。

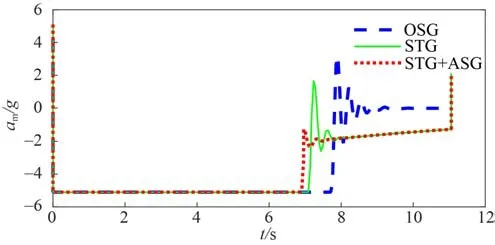
图2 导弹加速度Fig. 2 Accelerated speed of the guided projectile

通过制导律1、2 和3 的仿真，图3 和图4 说明所设计的制导律均能够使得滑模面误差和1 阶导数收敛至原点；图5 说明本文所设计的制导律均能够使导弹精确打击2 000 m 处的目标，落点精度均小于1 m；图6 说明所涉及的制导律均可以使导弹在接近目标时达到-80°弹道倾角，1 阶OSMG 落角 偏差为2°，2 阶STG 落角偏差为2.6°，均满足落角要求；图7 说明制导能够使导弹保持较小的视线角速度；图8 说明所设计的ASG 在发生加速度饱和时候开始动作，保证较小的加速度。

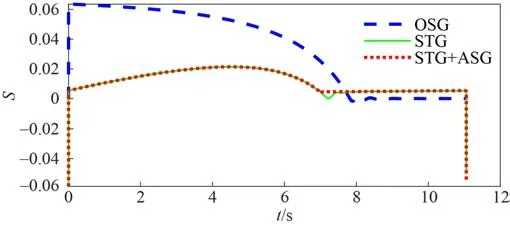
图3 滑模面误差Fig. 3 Sliding-mode surface error

图4 滑模函数的1 阶导数Fig. 4 Derivative of the sliding-mode surface

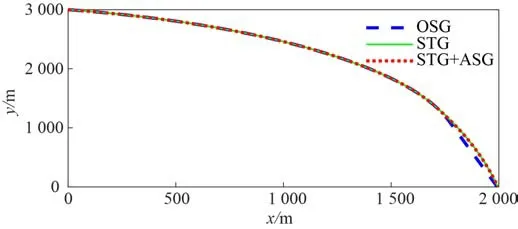
图5 导弹弹道曲线Fig. 5 Trajectory of the guided projectile

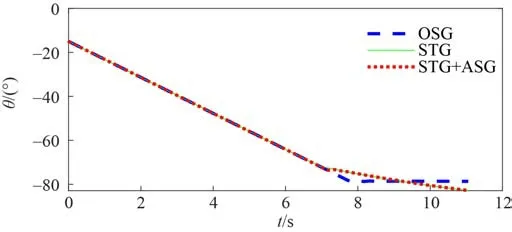
图6 导弹弹道倾角Fig. 6 Trajectory obliquity of the guided projectile

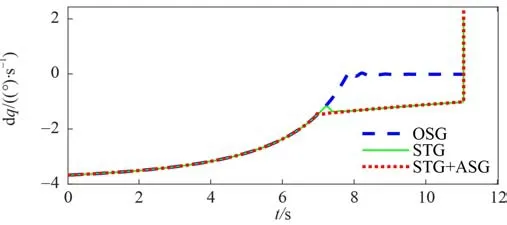
图7 导弹视线角速度Fig. 7 Line-of-sight velocity of the guided projectile

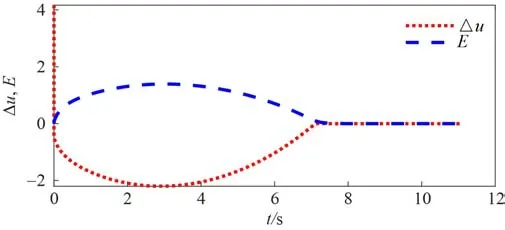
图8 辅助系统的输入和输出变量Fig. 8 Input and output variables of the auxiliary system

对比设置的3 种仿真方案，制导律性能概括为如下两点：

1)对比制导律1 和制导律2 的仿真结果，可以发现，如图3 和图4 所示，1 阶OSMG 在仿真开始9 s 达到收敛，而2 阶STG 在仿真开始7 s 就达到收敛，说明STG 能够提高收敛速度。

2)对比制导律2 和制导律3，通过图1 可以看出，在仿真开始发生加速度饱和时，ASG 开始作用，减小了加速度指令，并且能够在同样的时间内打中目标。

4 结论

本文将弹目相对运动方程转化为标准的2 阶系统模型，方便OSMG 推导设计。基于双曲正切切换函数，采用线性滑模面设计基于趋近律的1 阶OSMG。采用改进的超螺旋算法进行2 阶OSMG设计，有效地缩短了滑模状态变量的收敛时间。通过构造Lyapunov 函数分别对1 阶和2 阶OSMG 进行稳定性证明。在此基础上，采用辅助系统理论设计ASG，弱化加速度受限对制导系统的影响，并进行制导律的对比仿真。仿真结果表明，本文提出的自适应STG 能够在更短的时间内收敛，具备较高的制导精度，满足落点和落角要求；设计的ASG 在加速度受限的情况下也能够以期望的落角和落点精确命中目标，满足制导系统要求。