基于线性自抗扰的水下运载器控制

高全喜, 可伟, 乔海岩

(河北汉光重工有限责任公司，河北 邯郸 056017)

0 引言

对于强非线性、强耦合、参数不确定和多输入多输出的水下运载器而言[1]，控制系统设计尤为关键，决定着其航行品质的优劣。另外，在复杂多变的水下环境航行时，运载器易受到外环境干扰[2](如海流)，这些扰动严重影响到控制系统的动态稳定性与精度。

自抗扰控制(ADRC)方法[3]被韩京清提出后，由于其将存在内外扰的非线性系统还原为标准的“积分串联型”系统，从而提高控制性能的特 性[4-6]，在水下无人航行器领域有着广泛的应用前景。在简化水下航行器动力学模型基础上，文献[7]基于非线性自抗扰控制方法和遗传算法，对垂向位移和俯仰角控制进行研究，实了控制器参数自动整定。针对横滚姿态控制，文献[8]基于非线自抗扰对线性化后的水下航行器动力学模型进行了控制器设计。文献[9]基于非线性自抗扰控制方法，实现了水下无人航行器近水面航行控制。

对于非线性自抗扰控制技术而言，其参数的整定的数量较多[10-11]，给工程应用与实现带来了困难。Shen 等[12]将非线性自抗扰控制技术进行了线性化改进，提出了线性自抗扰控制(LADRC)方法。线性自抗扰控制理论只需整定控制器带宽以及扩张状态观测器带宽两个参数[13]，降低了控制参数整定的难度，且具有明显的物理意义与良好的控制效果[14-15]，更加利于工程实现。Fu 等[16]将线性自抗扰控制方法应用于导弹姿态控制系统，实现了导弹的高精度姿态控制。Xu 等[17]针对机翼-外储箱-燃油晃动的气动弹性系统，基于LADRC 设计了机翼颤振抑制控制器，实现了机翼颤振抑制。在水下航行器应用方面，当前线性自抗扰多用于单通道控制[18-19]，少有针对水下运载器多通道解耦控制方向的研究。

本文针对水下运载器非线性动力学模型不同通道之间的耦合问题，基于线性自抗扰控制设计了三通道解耦控制器，对该姿控方法进行稳定性分析。通过仿真验证该控制方法的有效性与鲁棒性。在加入海流干扰的影响下，与PID 姿态控制方法进行对比，以验证自抗扰控制器的性能。

1 水下运载器非线性动力学模型

作为本文的基础环节，首先基于动量矩定理在体坐标系Oxyz下建立水下运载器绕质心的转动方程。水下运载器绕质心转动的非线性动力学模 型[20]为

式中：Jxx、Jyy、Jzz为转动惯量；λ44、λ55、λ66为附加转动惯量；xc、yc、zc为质心坐标在体系下的分量；ωx、ωy、ωz为转动角速度；vx、vy、vz为体系下的速度；ρ为流体介质的密度；S、L分别为运载器最大横截面积与长度；为无量纲转动角速度；φ、ψ、θ分别为滚转角、偏航角以及俯仰角；α、β分别为攻角和侧滑角；m、G分别为运载器质量和重力；δd、δr、δe分别为滚转通道、偏航通道与俯仰通道的舵偏角；分别为横滚力矩系数对β、δd、δr、δe、以及的导数；分别为偏航力矩系数对β、δd、δr、δe、以及的导数；分别为俯仰力矩系数对α、δd、δr、δe以及的 导数。

运载器绕浮心的转动角速度为ωx、ωy、ωz，其欧拉角变换率为，可得到水下运载器姿态角与角速度的转换关系为

2 基于LADRC 的三通道姿态控制

基于LADRC 理论，本文提出的水下运载器三通道姿态控制器由内环角速度控制回路和外环姿态角控制回路组成。姿态控制指令通过外环控制器解算输出内环控制器的指令信号，再由内环控制器输出各个通道舵偏角。

2.1 姿态角回路控制器设计

水下运载器三通道姿控回路结构如图1 所示。图1 中，φc、ψc以及θc分别为水下运载器横滚通道、偏航通道和俯仰通道控制指令输入信号，经过外环LADRC 控制器解算得到各个姿态内回路的期望角速度。图1 中，U1为横滚通道控制外回路的虚拟控制量；U2为偏航通道控制外回路的虚拟控制量；U3为俯仰通道控制外回路的虚拟控制量；ωxc、ωyc以及ωzc分别为水下运载器横滚通道、偏航通道和俯仰通道内环角速度控制回路输入信号。

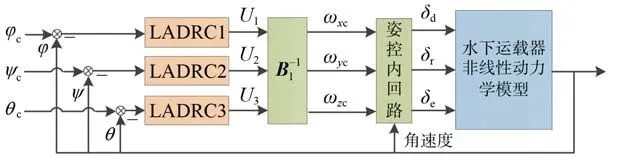
图1 基于LADRC 的水下运载器姿控回路Fig. 1 Attitude control loop of the underwater vehicle based on LADRC

针对姿控外回路单通道的多输入问题，结合 式(2)引入虚拟控制量：

式中：

由式(2)和式(4)，可得水下运载器姿控外回路的输入输出关系为

式中：x1为各个通道姿控外回路状态量；F1为姿控外回路总和扰动。

f1=f2=f3=0，x1、x2、x3为姿控外回路状态量。

由式(5)可知，外环各个控制通道的被控对象为1 阶系统，设计2 阶扩张状态观测器(ESO)对其状态量进行估计。因此，适用于水下运载器姿控外回路的LADRC 控制律为

式中：z1i、z2i为ESO 状态量；ri为各控制通道目标值；为1 的估计值；ESO 和控制器参数为，ω0i和ωci分别为外环姿态角控制回路观测器带宽和控制器带宽。

2.2 角速度回路控制器设计

水下运载器三通道解耦控制系统结构如图2 所示。由控制外回路得到期望角速度，经过解耦控制器可得到水下运载器的舵偏角，通过解算水下运载器非线性动力学方程得到其各个通道的状态量，最后将这些状态量反馈到各个控制通道完成闭环控制。图2中，Ud为横滚通道内环控制回路的虚拟控制量，Ur为偏航通道内环控制回路的虚拟控制量，Ue为俯仰通道内环控制回路的虚拟控制量。

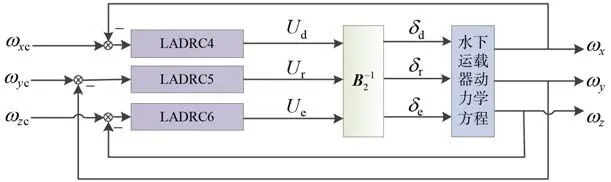
图2 水下运载器姿控内回路解耦控制框图Fig. 2 Decoupling control block diagram of attitude control inner loop of the underwater vehicle

将水下运载器各个通道的耦合量作为总和扰动，通过扩张状态观测器估计该总扰动，引入到反馈控制器中进行补偿，完成各个通道的解耦。针对姿控内回路单通道的多输入问题，结合式(1)引入虚拟控制量：

式中：

由式(1)和式(8)可得，水下运载器姿控内回路的输入输出关系为

式中：x2为各个通道姿控内回路状态量；F2为姿控内回路总和扰动。其中：

x4、x5、x6为姿控内回路状态量，f4、f5、f6为姿控内回路总和扰动。

内环各个控制通道的被控对象为1 阶系统，设计2 阶ESO 对其状态量进行估计。因此，适用于水下运载器内环控制回路的LADRC 控制律为

式中：ri为内环各控制通道目标值；为的估计值 。 ESO 和控制器参数为。 其中：ω0i和ωci为分别为内环控制回路的扩张状态观测器带宽和控制器带宽。由式(7)和式(11)可得基于LADRC 的水下运载器三通道姿态控制系统需整定6 个控制参数。

由式(7)和式(11)可知，自抗扰控制不依赖于被控制对象的精确数学模型。而文献[1]基于非线性动态逆的姿态控制方法依赖于精确的航行器动力学模型。与文献[7-9]基于非线性自抗扰理论的航行器控制方法相比，本文基于线性自抗扰控制理论所提出的姿态控制方法，算法更简洁，控制参数数量少且易整定，更适合于实际工程应用。

2.3 稳定性分析

基于前文建立的水下运载器动力学方程，分析了ESO 的收敛性。以横滚通道内环控制回路为例，由式(11)可知ESO 估计误差为

由式(11)和式(12)可得ESO 估计误差对时间的导数为

将式(13)写为矩阵形式

式中：各个矩阵表达式为

定理1假定滚转通道的有界，则存在常数ai＞0和ω01＞ 0，对于，满足,i=1, 2。

证明式(14)微分方程的解为

令

则存在时间T，对于 ∀t≥T＞0，下式所列不等式关系成立。

式中 ：i= 1,2，j=1,2。 由于有界 ，则成立，κ为一个正实数。因此，对于及i=1,2，式(20)所列不等式关系成立。

对于 ∀t≥T＞ 0及i=1,2，由式(14)~式(20)得

证毕。

由式(21)可知，在横滚通道上，扩张状态观测器的对ωx以及f4的估计误差上界随ω04单调减小，即ESO 是收敛的。同理，其他通道控制器的ESO 是收敛的。

3 仿真分析

水下运载器数字仿真的初始条件为：航速 20 kn、初始俯仰角为0°、初始偏航角为0°，初始滚转角为0°。俯仰、偏航、滚转三个通道的舵角限幅分别为30°、25°以及5°。分别在理想环境、水动力参数拉偏 ±30%、转动惯量拉偏 ±30%以及存在海流干扰的条件下进行计算，以验证本文提出的控制方法的有效性以及鲁棒性。

3.1 理想环境下的仿真计算

在理想环境进行仿真计算，各个通道目标值如图3 虚线所示。则水下运载器三通道姿态跟踪响应、舵偏角以及扩张状态观测器对状态量估计的计算结果如图 3~图 7 所示。

图3 横滚、偏航与俯仰通道姿态角响应曲线Fig. 3 Attitude angle response curves of roll, yaw and pitch channels

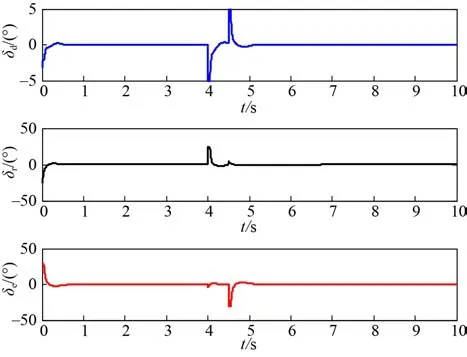
图4 横滚、偏航与俯仰通道舵偏角曲线Fig. 4 Ruder deflection curves of roll, yaw and pitch channels

由图 3 可知，在三通道相互耦合的影响下，运载器俯仰通道和偏航通道姿态能够快速且无超调对控制指令进行响应。受其他通道影响产生的滚转角，在控制器的作用下被快速归零。由图 5~图 7 可知，本文所设计的扩张状态观测器可以对水下运载器的姿态角、姿态角速率以及总扰动进行估计。可见本文基于LADRC 所设计的运载器控制系统具有良好的控制精度，能够对系统状态量进行精确估计。

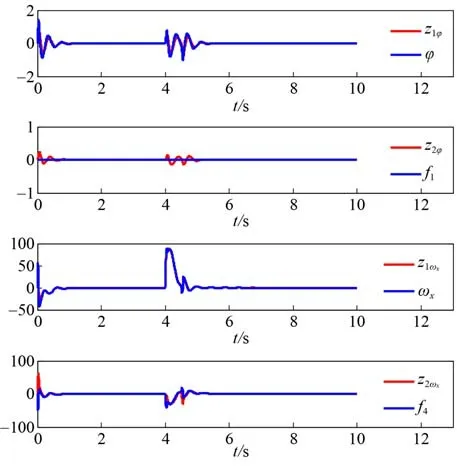
图5 ESO 对横滚通道状态量估计Fig. 5 State estimation of rolling channel by ESO

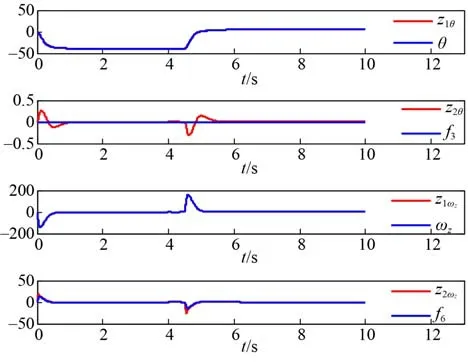
图7 ESO 对俯仰通道状态量估计Fig. 7 State estimation of pitch channel by ESO

3.2 LADRC 的鲁棒性验证

为验证LADRC 的鲁棒性，分别将水下运载器的水动力参数和转动惯量拉偏 ±30%。运载器三通道姿态角跟踪响应结果如图 8 和图 9 所示。仿真结果表明，在水动力参数和转动惯量参数存在 ±30%偏差的影响下，水下运载器各个通道姿态能够快速对控制指令进行响应。可见本文基于LADRC 设计的运载器控制系统具有良好的控制精度与鲁棒性。

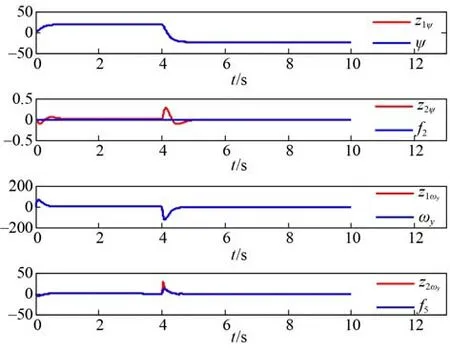
图6 ESO 对偏航通道状态量估计Fig. 6 State estimation of yaw channel by ESO

图8 水动力参数拉偏±30%Fig. 8 Hydrodynamic parameter deviation by ±30%

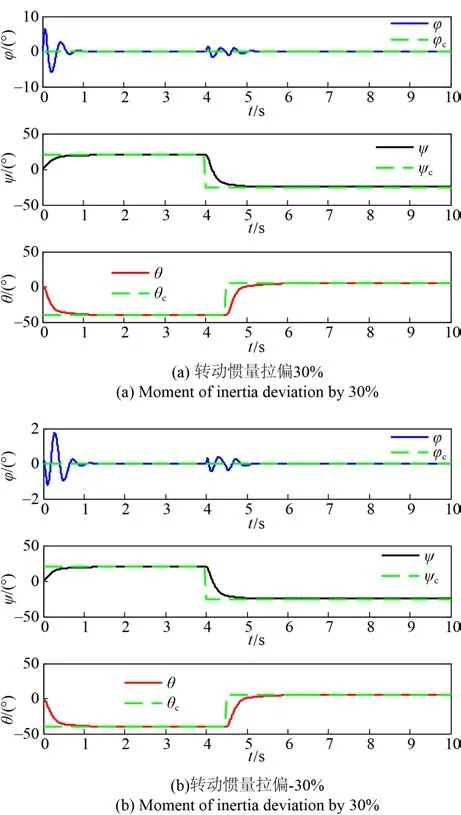
图9 转动惯量拉偏±30%Fig. 9 Moment of inertia deviation by ±30%

海流干扰是水下运载器设计过程中需考虑的一种外部干扰。在实际航行过程中，由于海流的影响，水下运载器弹道轨迹将发生变化。因此，本节在水下运载器三通道航行仿真过程中加入了海流干扰，并与传统的PID 姿态控制方法进行对比，以验证本文提出的控制器能否在海流干扰下对姿态进行精确控制以及有效性。

假定海流为定常均匀流场，则海流数学模型[20]简化为

式中：vw为海流在地面系的速度；vwx0、vwy0、为海流在地面系的速度分量；i0、j0、k0分别为地面系x轴、y轴、z轴的矢量方向。

3.3 海流干扰下的控制结果

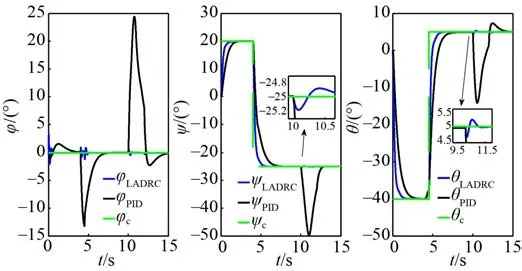
图10 海流干扰下的姿态响应Fig. 10 Attitude response under ocean current disturbance

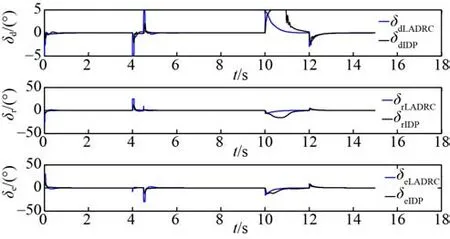
图11 LADRC 与PID 的舵偏角曲线Fig. 11 Rudder deflection curves of LADRC and PID

由PID 以及LADRC 的控制效果对比图可知，LADRC 比PID 控制器有更好的动态性能，运载器俯仰通道和偏航通道响应时间更短。10~12 s 航行时刻加入海流干扰，在PID 和LADRC 两种控制器作用下，运载器姿态均出现偏差。由图10 的局部放大曲线可得，PID 控制器作用下的运载器3 个控制通道出现了较大的姿态角偏差，姿态角偏差均大于10°，可见PID 控制器易受外界干扰，鲁棒性较差。而本文所设计的LADRC 姿态控制器具有更高的精度，产生的姿态角误差小于0.5°，快速消除了海流干扰引起的误差。可见在海流干扰下，基于LADRC 设计的运载器姿态控制器有较高的控制精度以及较强的鲁棒性。

3.4 不同干扰条件下的控制效果横向对比

图12 为理想环境、水动力参数拉偏30%、转动惯量拉偏30%以及存在海流干扰条件下的对比图。图12 中下标0、1、2、3 分别对应理想环境、水动力参数拉偏30%、转动惯量拉偏30%以及海流干扰。由横向对比图可知，在不同干扰条件下，各个通道都可对控制指令快速响应，控制系统具有良好的抗干扰能力。

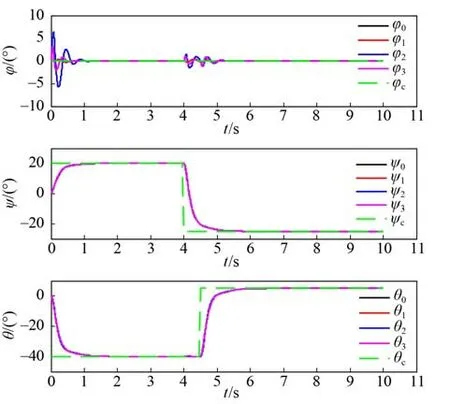
图12 不同干扰条件下的横向对比Fig. 11 Horizontal comparison under different disturbance conditions

前文的数字仿真基于20 kn 航速，为验证本文的姿态控制方法在较低航速下仍适用，在5 kn 的航速下进行仿真，计算结果如图 13 所示。

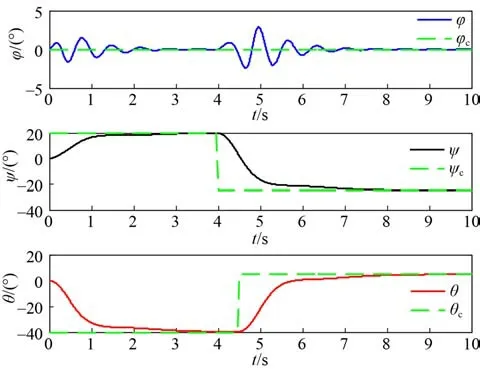
图13 5 kn 航速下姿态角响应曲线Fig. 13 Attitude angle response curves at 5 kn speed

在5 kn 的航速下，运载器俯仰角和偏航角能够快速且无超调对控制指令进行响应。受其他通道耦合产生的滚转角，在自抗扰控制器的作用下被快速消除。由此可知，在较低航速下本文所设计的三通道姿态控制器具有良好的控制精度。

4 结论

本文针对水下运载器非线性动力学模型，基于线性自抗扰控制实现了三通道解耦控制，并分析了控制器的稳定性。数值仿真表明，本文提出的控制方法具有良好的控制效果，能够精确估计系统状态量。在水动力参数和转动惯量参数存在 ±30%偏差的影响下，运载器姿态能快速响应控制指令。在海流干扰下，相较于PID 控制器，基于LADRC 设计的运载器姿态控制器具有较高的控制精度以及较强的鲁棒性。