基于粗糙集和随机森林算法的数学师范生就业预测研究

刘亚琴，刘瑞卿，颜中玉

(湖南师范大学数学与统计学院，计算与随机数学教育部重点实验室，中国 长沙 410081)

“就业是根本民生问题”[1]。作为就业大军中的主力，2020—2022年高校毕业生规模分别约达874万人、909万人和1 076万人，毕业生规模与增量不断攀升。此外，在新冠肺炎疫情冲击下，就业岗位数量严重缩水，为大学生就业带来的挑战更为严峻。

不断蓬勃发展的教育事业，使得教师职业得到人们的重视和普遍认同。此外，越来越多的人将教师作为职业首选，主要归结于其职业稳定性以及社会地位和薪酬的提升。师范生一般被划分为公费师范生和普通师范生，其区别在于公费师范生按照协议就业，无需担忧毕业后的去向，故而在本文中所提到的师范生均指代普通师范生。师范类毕业生就业面窄和就业质量下滑等问题已成为高校就业工作的难中之难[2]。在普通高校毕业生就业竞争日趋激烈的背景下，师范类毕业生在就业市场可能会处于更为复杂和艰难的境地。这也倒逼师范专业学生必须不断提升自身素养，在就业市场中保持竞争力。

为提升人才培养质量，坚持以高素质、专业化为目标培养教师队伍，教育部在2017年10月正式颁发了《普通高等学校师范类专业认证实施办法(暂行)》，随着该政策不断深化推进，目前已在全国高校全面铺开，其基本理念成为高等师范院校专业改革发展的重要参照。根据师范专业认证要求，许多师范院校调整优化了师范类本科专业培养方案。因此，以师范生培养的成效为导向，从师范生就业发展出发，反向设计课程体系和教学环节，对于优化师范专业培养布局，振兴教师教育具有重要意义。

随着就业问题关注度不断提高，就业质量影响因素和就业预测等方面的研究不断深入。就业质量影响因素包括个人特征、高校声誉、家庭社会资本和经济发展等[3]。个人特征主要包括性别[4]、生源地、学历、职业认同感、就业能力、实习经历[5]等因素，是影响就业的内在因素；高校声誉是影响毕业生就业质量的关键因素之一，毕业生的就业质量与高校声誉成正比[6]，与学校的历史积淀、师资力量和教学科研水平息息相关。家庭社会资本作为毕业生可以借助的强关系，家庭社会关系的广泛程度、父母资源动员能力和家庭经济[7，8]等因素均会对毕业生就业质量产生直接影响。经济水平是外部因素的重要层面，分析表明，城市的经济发展水平、产业结构、私营企业发展状况、就业工资等是影响毕业生就业的主要因素[9]。对此，哪些因素影响大学生就业满意度[10]，如何提升就业质量[11]已成为当前研究关注的重点。

随着大数据技术的发展，利用数据分析挖掘的方式来分析社会需求和就业影响机制[12-16]，是提升就业质量的有效途径，许多学者基于数据分析，通过就业预测的方法找出影响大学生就业质量的关键因素，进而为高校就业指导和人才培养方案制订提供了科学依据。多元回归分析[17]是就业预测的常用方法，其优点是简单和方便，但精度不高，推广适用性差；灰色系统模型[18，19]能够可克服多元回归分析的缺点，对样本的限制少，就业预测的精度高推广性好，但模型较复杂，运算过程慢耗时较长。近年来，基于机器学习的方法来分析毕业生就业数据的优势逐渐显现，基于神经网络[20]、决策树[21]、贝叶斯[22]等算法构建的就业预测模型，获得了较好的预测结果，特别是基于粗糙集算法模型[23]，能够较好地挖掘数据中潜在的规则和知识，进一步提高了预测精准度。

基于上述背景，本文应用粗糙集理论和随机森林算法构建数学师范生就业预测模型，分析影响数学师范生就业的关键影响因素，可为数学师范类毕业生就业指导提供有价值的参考。

1 方法介绍

1.1 粗糙集

粗糙集理论基于等价关系，描述了任意对象之间的不可分辨关系，其在数据分析方面有着许多优势，例如可以识别统计方法无法发现的关系，适用定性和定量数据以及根据数据直接确定决策规则等。以下给出粗糙集方法的几个基本定义。

定义1建立一个信息系统IS=〈U,A,V,f〉,P⊆A,U/P={X1,X2,…,Xn}。其中P的香农熵H(P)被定义为

(1)

定义2给定一个信息系统IS=〈U,A,V,f〉,P,Q⊆A,U/P={X1,X2,…,Xn},U/Q={Y1,Y2,…,Ym}。其中，P和Q的联合熵定义为

(2)

定义3设DS=〈U,C∪D,V,f〉为一个决策系统，C作为条件属性集，D作为决策属性集，B⊆C,U/B={X1,X2,…,Xn}且U/D={Y1,Y2,…,Ym}。在B条件下D的条件熵定义为

(3)

定义4设DS=〈U,C∪D,V,f〉为一个决策系统，该系统中C作为条件属性集，D作为决策属性集，B⊆C,U/B={X1,X2,…,Xn}且U/D={Y1,Y2,…,Ym}。B和D的互信息定义为

I(B;D)=H(D)-H(D|B)。

(4)

定义5设DS=〈U,C∪D,V,f〉为一个决策系统，该系统中C作为条件属性集，D作为决策属性集。B⊆C,∀a∈C-B，属性a的增益Gain(a,B,D)被定义为

Gain(a,B,D)=I(B∪{a};D)-I(B;D)=H(D|B)-H(D|B∪{a})。

(5)

粗糙集增益约简算法为

Step 1.令B=Ø；

Step 2.选择任一属性a∈C-B，计算Gain(a,B,D)；

Step 3.选择使得Gain(a,B,D)取到最大时的属性记为a；

Step 4.若Gain(a,B,D)>0，则将B∪{a}赋予B，回到第二步，否则进行下一步；

Step 5.集合B就是选定的属性。

1.2 随机森林算法

随机森林算法是Breiman[24]在Bagging算法和集成学习思想的基础上所提出的一种统计学习理论，它利用Bootstrap组合多个互不相关的决策树，最后基于多种决策树组合通过投票或取均值的方法得到预测结果并输出。森林的泛化误差随着森林中树木数量的增加而收敛到一个极限。其中，模型分类器的泛化误差取决于森林中单个树木的强度和它们之间的相关性。使用特征的随机选择来分割每个节点产生的错误率优于Adaboost。

随机森林算法的详细流程如图1所示，基于原始样本集，使用Bootstrap进行M轮有放回地随机抽取训练样本，得到M个子样本集；对于M个子样本集，随机选取特征，训练M个决策树。样本有放回地随机抽取以及构建决策树时特征随机选择，保证了随机性，使得模型过拟合的概率降低，具有很好的泛化能力；而森林拥有多个决策树，且采用集成算法，精度要优于大多数单个算法。“随机”和“森林”使得输出结果通常具有较高泛化性能和精确度。

图1 随机森林算法流程 Fig. 1 The flow of random forest algorithm

2 实证分析

2.1 研究样本和数据来源

本文以国内某高校(下文以A校代替)2019届、2020届的数学与应用数学(普通师范生)本科毕业生为研究对象，搜集了学生大学四年期间的课程成绩、综合测评成绩以及毕业去向等信息，其中毕业去向情况来自于该省大中专学校学生信息咨询与就业指导中心毕业生派遣数据库。剔除异常值并排除留级生后，共获得有效数据480条。

2.2 数据预处理

学生的毕业去向被划分为4类：就业、升学、出国、待就业。由于升学和出国可以理解为国内深造和国外深造，延长了受教育年限，等同于推迟就业，所以本文对这两种毕业去向不予以讨论。经过整理，在剩余数据中，学生的毕业去向被划分为两类：就业和待就业。最后得到2019届毕业生就业数据102条，2020届毕业生就业数据100条。

数学与应用数学本科专业课程共计39门，参考A学校该专业的培养方案，将课程分为9个模块，分别为专业核心课程、学科基础课程、学科教育类课程、基础课程、公共必修课、教师技能课程、教育实践课、专业实践课程和素质实践。各模块的分值由课程分值和相应的学分加权平均得到，其中素质实践不计分，主要考察基本素质、创新素质与实践能力两个方面。变量分组如表1所示。为便于利用粗糙集方法进行计算，对成绩数据做离散化处理，80分及以上记为“1”，60～79分记为“2”，60分以下记为“3”。

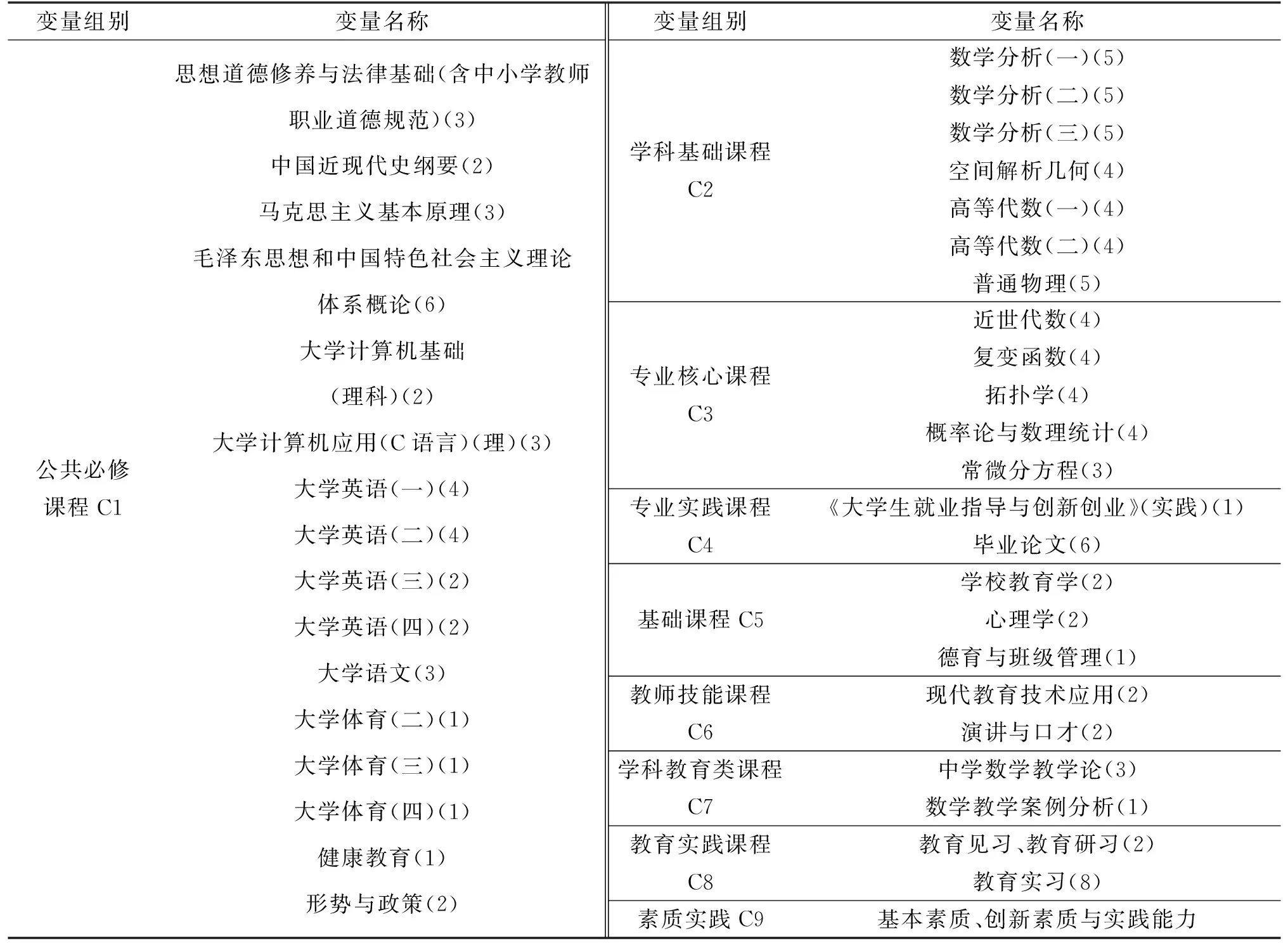
表1 变量分组

2.3 粗糙集属性约减

基于粗糙集理论基本方法，构建数学师范生就业信息系统，其中条件属性为专业核心课程、学科基础课程等9个自变量，决策属性为就业状况，决策信息表如表2所示。

表2 决策信息表

基于上述粗糙集增益算法，利用Matlab对各条件属性进行属性约简，约简过程如表3所示，图中每一轮标识的属性为该轮计算后保留的属性。通过计算，得到对于决策属性(就业状况)而言各成绩模块的条件属性约简结果。由表3可见，当取到属性C8(教育实践课程)时，增益值最大值为0，故将属性C8剔除，最后得到约简结果为{专业核心课程、学科基础课程、基础课程、公共必修课程、教师技能课程、学科教育类课程、专业实践课程、素质实践}，据此筛选出对于就业影响较为重要的自变量。

表3 属性约简过程

由表4可见，被约简的教育实践课程相比其他指标，其离散系数较小，该课程对于学生就业的区分度不大，其主要原因是该课程评分过于宽松，导致学生在该项课程得分高且较为接近。因此，教育实践课程的评分标准需进一步改进，使其能够真实反映学生教育实践水平，也有利于就业指导部门能够更有针对性地为学生提供帮助。

表4 描述性统计分析

2.4 随机森林预测模型

2.4.1 随机森林模型的构建 选择2019届毕业生的数据(102个)作为训练集，2020届毕业生的数据(100个)作为测试集，用于检验模型的预测效果，对于就业状况的处理，设就业为“1”，待就业为“0”。基于上述数据，借助Python语言，依托国际上流行的机器学习开源工具包Scikit-learn中的分类器RandomForestClassifier构建随机森林模型。

随机森林算法中需要设定的重要参数包括决策树的数量(n_estimators)、树的最大深度(max_depth)、最小样本划分数量(min_samples_split)和最小叶子节点数量(min_samples_leaf)。

在基础随机森林模型中，其参数均设为默认值。通过训练集的特征和实际分类结果训练模型，得到训练后的分类器，代入测试集数据进行预测，采用准确率来评价分类器性能。该模型的预测准确率为0.8，预测能力较好。为寻找最优模型参数、提升预测精度，采用多参数网格搜索法估算出分类器的参数。该方法是基于各参数变量值的可取范围，逐步细分为若干区间，随后按照顺序算出各参数变量值组合所对应的误差目标值，并对结果逐一比较筛选出最优值，从而确定该区间内最小误差及其对应的最佳参数值。从原理上可以看出该方法的估值基本是得出了全局最优解，尽可能地缩小了误差。通过网格搜索法调参，为分类器选取的最优参数如表5所示。

表5 参数估值结果

2.4.2 随机森林模型预测结果分析 利用参数调优后的分类器重新基于2020届毕业生的成绩和综合测评数据对毕业状况进行预测，预测准确率提升至0.83。该研究利用2019届毕业生的数据对分类器进行训练，从而实现了对2020届毕业生就业情况较为准确的预测，这为如何制订协助大学生就业的策略提供了数据分析层面的支撑，负责大学生就业的有关部门可以通过对其学习成绩的分析和预测，提前发现问题，有针对性地进行就业辅导与帮助。

通过特征重要性评估，对各模块进行就业预测的重要性计算，结果如图2所示。各模块的重要性排序由大到小为：素质实践, 专业核心课程, 基础课程, 教师技能课程, 学科基础课程, 学科教育类课程, 专业实践课程, 公共必修课程。从结果来看，素质实践、专业核心课程、基础课程、教师技能课程和学科基础课程模块较为重要，特别是素质实践能力对于师范类毕业生就业起到了首要作用。

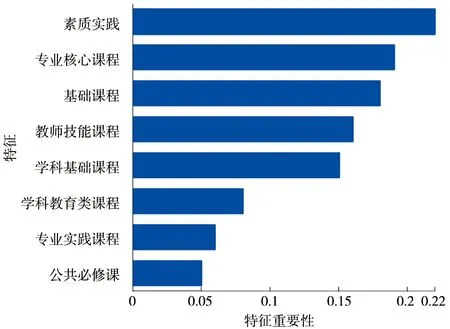
图2 特征重要性排序 Fig. 2 Feature importance ranking

3 结论与对策

本文采用了粗糙集和随机森林算法，对学生成绩和综合测评数据进分析，结果表明，该算法能有效预测数学师范生就业能力，利用预测模型，可以较为准确地通过学生成绩来预测其未来的就业情况。为更好地促进师范生就业提出以下几点建议：

(1)提升学科素养，引领专业成长。专业核心课程体现的是学科素养，高校需注重培养学生扎实的数学学科知识，掌握数学的思想与方法。学科素养高的师范生在就业领域具有较强的职业发展潜力和竞争力。换言之，学科素养是用人单位对毕业生职业能力评价的核心要素。

(2)坚持实践育人，培养创新人才。素质实践主要涵盖了创新素质与实践能力，因此要加强创新和实践教育的顶层设计，一方面打造学科竞赛平台，开展创新实践。依托数学竞赛、数学建模竞赛和师范生教学技能竞赛等培养数学应用创新人才。另一方面提供志愿服务平台，开展社会实践。鼓励学生走进社区、走进基层，大力推进社会实践和志愿支教活动。

(3)彰显师范特色，夯实教学技能。持续重视教师教育类课程，充分考虑师范类院校 “教师教育特色鲜明”的办学定位，优化教师教育课程结构，改革课程教学内容，推动教育实践环节质量考核，提升数学师范生的教育教学能力。

此外，考虑到粗糙集和随机森林算法具有较强的适用性，该方法还可推广至其他专业的本科生和研究生的就业预测。