基于CNN 机翼气动系数预测

吕召阳，聂雪媛，*，赵奥博

(1.中国科学院 力学研究所，北京 100190；2.中国科学院大学 工程科学学院，北京 100049)

传统机翼气动参数的获得方法可以归结为2 种：采用风洞试验测量和计算流体力学建模计算。但是这些方法存在高成本、计算量大和测试周期长等问题[1-2]。所以，如何实现机翼状态改变后气动参数的快速预测成为了实现颤振主动控制的一大难点。

传统快速预测方法的基本思想是根据气动参数的统计规律，利用数学拟合的方法得到几何参数与飞行状态和气动参数的数学关系式，从而实现气动参数的快速计算，但这种方法一般适用范围较小，并且对存在很强非线性问题的系统不能很好保证预测精度[3]。随着最近几年神经网络的快速发展，其突出的非线性映射能力吸引越来越多的学者将此方法运用到气动参数预测上。2003 年Suresh等[4]基于递归神经网络建模，预测大迎角下旋翼的升力系数并与试验数据进行比较，证明了其方法的可行性。2011 年Carpenter 等[5]提出一种单隐含层的神经网络用于导弹气动参数的预测。刘昕[6]提出一种基于径向基函数的神经网络（radial basis function neural network，RBFNN）模型，并将其成功运用到机翼沉浮振动的升阻力预测中。原智杰等[3]基于优化的反向传播（back propagation ，BP）神经网络进行了导弹的气动参数预测，证明了其方法有较好的泛化和拟合能力。Balla 等[7]提出了一种多输出的神经网络来进行二维和三维机翼的气动系数预测，并与本征正交分解（proper orthogonal decomposition，POD）方法进行了比较，结果表明神经网络具有更好的性能，特别是在预测包含激波的流场中。

神经网络虽然在气动参数预测中表现出可喜的结果，相比于传统拟合方法具有较好的非线性拟合能力，但对于文献[3-7]所提到的研究，在进行模型训练时都需要先对机翼进行参数化处理，这无疑给模型的建立和训练增加了困难。如果模型能直接将机翼状态图片作为训练对象，则将大大降低模型的建立和训练难度。在众多机器学习方法中，卷积神经网络可以将图片直接作为训练对象，并且具有强大的非线性映射能力和自动提取流场特征的功能[8]，这无疑给本文研究提供了方向。陈海等[9]基于卷积神经网络建立了单输入单输出的模型，对不同翼型的升力系数进行了预测并通过对预测结果的误差分析证明了其方法的有效性。然而对于机翼颤振控制一类的问题而言，其翼型并不改变，结构相对其平衡位置的空间状态发生改变，如何基于卷积神经网络对这类问题进行多变量输出的气动参数预测的研究尚未开展。

针对文献[3-9]研究现状，本文基于卷积神经网络（convolutional neural network，CNN)，以二维翼型为对象，建立一种基于卷积神经网络的多变量多输出预测模型，用于实现对机翼气动参数的快速预测，最后通过测试集上的预测结果和计算流体力学（computational fluid dynamics，CFD）的计算结果进行误差分析，对本文所提气动参数预测模型的有效性和准确性进行验证。

1 CNN 理论与建模

随着深度学习的快速发展，以及其突出的非线性映射能力，越来越多的学者将机器学习方法运用到流体力学领域。其中由于卷积神经网络具有强大的图像特征提取和非线性映射能力，因此，卷积神经网络成为当下流场预测及流场特征研究中不可忽视的工具。卷积神经网络主要组成部分包括：输入层、卷积层、池化层、激励层、全连接层及输出层。其中具有代表性的卷积神经网络如LeNet，如图1 所示。

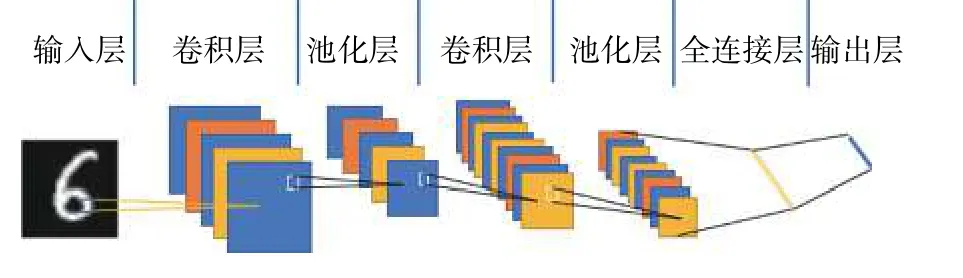
图1 LeNet 卷积神经网络经典结构Fig.1 Classic structure of LeNet convolutional neural network

目前虽然提出了许多经典的卷积神经网络框架，但是卷积神经网络的框架并不是一成不变的，可以根据具体问题加以设计。本文针对建立气动参数快速预测模型，为颤振主动控制过程服务这一具体问题，基于卷积神经网络原理建立了一种多变量多输出的预测模型，其具体结构为

1）输入层。目的是实现机翼颤振控制过程中机翼的不同状态下（包括迎角和沉浮）的气动参数快速预测，为了保留机翼的状态信息和简化数据处理过程，模型的输入数据采用机翼状态改变后的原始图像，同时将在这一状态下经过CFD 计算出的升力和力矩系数作为标签。具体形式如图2 所示，图下方数字分别为图的编号，升力系数，阻力系数。

图2 基于RBF 网格变形机翼状态图及升力和力矩系数Fig.2 Deformed wing state diagram and lift drag coefficient based on RBF mesh

2）卷积层。卷积层是卷积神经网络的核心层。虽然卷积层数越多、网络深度越深训练出的网络模型预测精度越高，但考虑实际情况和训练成本，所建立的网络采用3 层卷积层。

3）池化层。卷积神经网络池化层的设置不仅可以减少网络的计算量，从而很大程度上节约训练的时间成本，而且还能在一定程度上防止模型过拟合的发生[10]。池化操作一般包括均值池化（对滤波器大小区域不为零像素点取均值）和最大池化（对滤波器大小区域所有像素点取最大值），其中均值池化算法得到的特征数据对背景信息比较敏感，最大池化会对数据纹理特征信息更加敏感。结合本文要解决的问题，模型的池化层采用最大池化的方法和下采样的方式，即在卷积层后接一个池化层，以达到减小计算量和防止过拟合的目的。

4）激励层。激励层的设置是神经网络能更好实现非线性映射的基础。饱和的非线性激励函数是传统神经网络经常使用的函数，包括sigmoid、tanh和softsign 函数[11-12]，但近几年研究发现，不饱和非线性激励函数（ReLU)相比传统饱和非线性激励函数具有更为出色的收敛速度，所以不饱和非线性激励函数逐渐得到学者的亲睐[13-14]。为了能得到更好的收敛速度，模型将选用ReLU 作为激励函数，ReLU 函数表达式为

式中：x 为自由变量。

为了能更好地拟合机翼状态与机翼升力及力矩系数的映射关系，整个网络的输出层采用tanh 非线性激励函数，其函数表达式为

5）全连接层。全连接层是卷积神经网络能进行后续处理和采用梯度下降法进行网络参数训练的基础。由于涉及到的问题需要同时预测出2 个未知量，所以建立的卷积神经网络采用并列2 个全连接层分别实现升力系数和力矩系数的预测。

6）输出层。建立卷积神经网络的目的是实现机翼升力和力矩系数的同时快速预测。因此，模型设置2 个输出层。

本节分别介绍了卷积神经网络每层的作用和所建立的卷积神经网络每层的设置细节。除此之外，为了能使所建立的卷积神经网络更好的避免过拟合问题，除了在每层卷积层后面接池化层外，还在全连接层后设置了dropout 层(其中在训练过程中keep_prob=0.5，测试过程中keep_prob=1)。因此，建立的卷积神经网络具体结构和参数设置如表1所示。

表1 差积神经网络具体结构和参数设置Table 1 Specific structure and parameter setting of CNN

2 气动弹性系统模型

本文研究的目的是利用卷积神经网络理论建立气动参数快速预测模型，为颤振主动控制过程服务，所以计算训练样本的研究模型选取颤振研究中常使用的二元翼型，如图3 所示[15]。

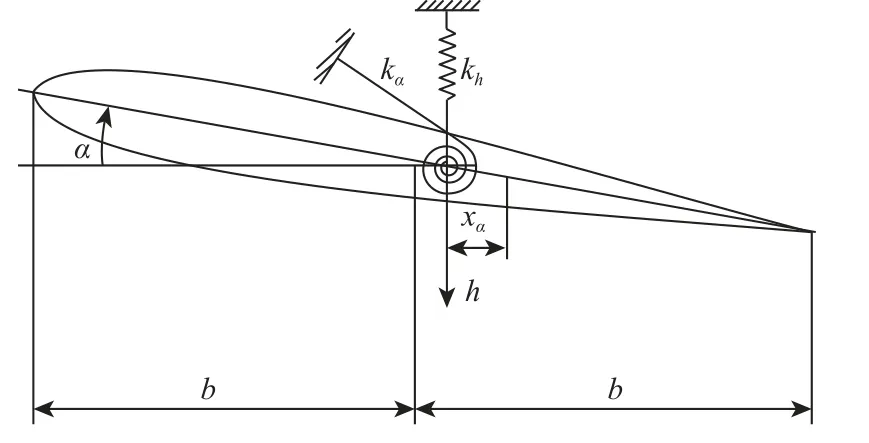
图3 二元翼型[15]Fig.3 Two dimensional airfoil[15]

对二元翼型进行受力分析，其非线性控制方程可以表示为

式中：h 为沉浮位移；α 为俯仰角；kh为沉浮方向刚度系数；kα为俯仰方向刚度系数；Iα为机翼惯性矩；m 为机翼质量；xα为弹性轴到机翼重心的无量纲距离；b 为机翼半弦长；L 和M 分别为气动力简化到机翼质心上的力和力矩。

从式（3）可知，求解方程只需获得机翼所受的气动力便可，又因气动力可以化简为气动升力L，和力矩M，因此，通过获得机翼升力系数CL和力矩系数CM（单位体积流体在机翼面上产生的升力和力矩）也可以实现机翼气动力的计算。因此，可将如何获得气动力来求解控制方程的问题，进一步转变成如何获得机翼升力和力矩系数来求解控制方程的问题。

为了给第1 节所建立的卷积神经网络模型提供训练数据，基于RBF 网格变形理论通过CFD 计算获得机翼不同迎角和浮沉下的升力和力矩系数和几何外型，分别作为后续卷积神经网络的训练输入和标签。其中气动计算采用的是基于雷诺平均二维Navier-Stokes 方程（Reynolds equation，RANS），其守恒的流动方程可以表示为

式中:S 为控制体体积；Q 为守恒通量；l 为控体体边界；Gc为对流通量；Gv为粘性通量；n 为表面法向量。

3 机翼升力系数预测及模型性能测试

3.1 模型的训练

对于卷积神经网络来讲，所取的训练数据在所运用工况范围分布越均匀其训练出的模型精度越高、稳定性越好、适用性越强。因此，本文基于拉丁超立方抽样方法在所要涉及的工况范围内随机抽取了1 100 个工况条件,以保证训练数据在工况范围内的随机性和均匀性，其工况分布如图4 所示。并利用编写的基于RBF 网格变形程序结合Fluent对所抽取的工况进行计算，其计算结果作为训练和预测验证的数据。为了能更充分的体现所建立的卷积神经网络的性能，在这些计算工况中又随机选取70 个工况数据做为测试集，剩余的1 030 个工况数据作为训练集。模型训练方法采用TensorFlow中提供的Adam 算法优化器，其中学习率设置为1×10-5，为了提高训练效率，数据分10 批输入，每批103 个样本。卷积核的初始化采用标准差为0.01的正态分布随机数，偏执初始化采用标准差为0.1 的正态分布随机数。模型误差判断标准采用均方根误差RMSE，其具体表达形式为

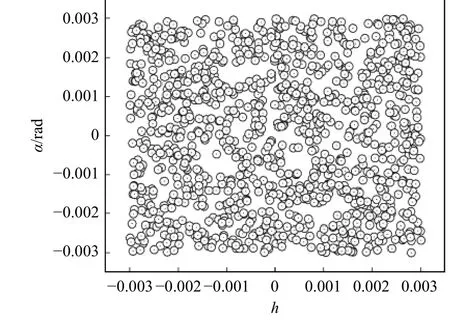
图4 样本工况分布点Fig.4 Distribution points of sample working conditions

式中:N 为每批训练样本的数量；observedt为CFD 计算出的真值；predictedt为卷积神经网络的预测值。

神经网络模型训练结束的条件可设置为达到最大迭代次数或达到精度要求。为了能获得更好的模型预测精度，同时避免模型训练时间过长，采取固定迭代次数的方法来控制模型训练的结束，其中迭代次数设置2 000 次。所用到的建模和训练的工作站配置为Intel(R) Core(TM) i9-10 900 K CPU @3.70 GHz(3 696 MHz)，128 GB 内存，显 卡 NVIDIA GeForce RTX 3 090 (24 576 MB)。采用GPU 的方法对模型进行训练，因为其训练速度比CPU 训练大约快12 倍。模型训练具体流程如图5 所示。

图5 CNN 训练流程Fig.5 CNN training process

3.2 结果分析

通过利用训练集进行模型的训练，其模型训练过程中升力和力矩系数的RMSE 都是逐渐降低的，图6（a）和图6（b）分别为训练过程升力和力矩系数最后一批前500 次迭代过程中的误差变化曲线，从图6 中可以看出误差变化是随迭代次数的增加而逐渐降低，虽模型在训练到500 步误差降低速度逐渐变缓，但也是呈下降趋势。

图6 训练过程中误差变化曲线Fig.6 Error variation curve during training

模型完全训练结束后，为测试模型训练的预测效果和预测精度，将未参与训练的工况数据输入到训练好的模型中进行机翼的升力和力矩系数的预测，预测结果如图7（a）和图7（b）所示，由图7 可知，预测值和CFD 的计算值几乎重合。但为了更好地分析其模型的预测精度，本文计算了预测值和真值的预测误差，如图8 所示，从图8 中可以看出不管是升力系数还是力矩系数，其预测误差都不超过2.5×10-3。

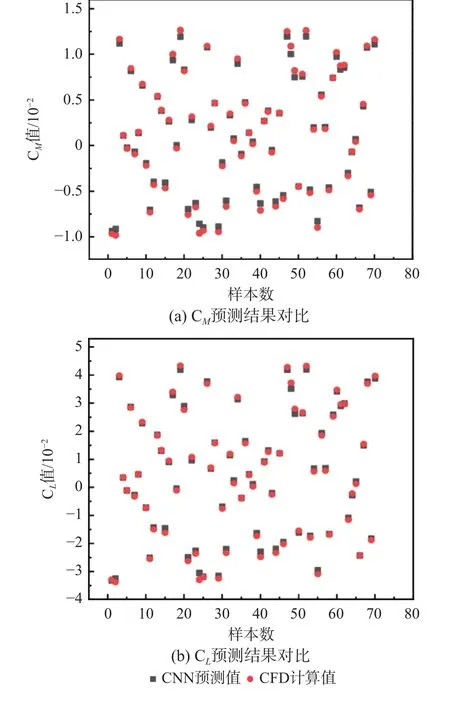
图7 预测结果Fig.7 Prediction results

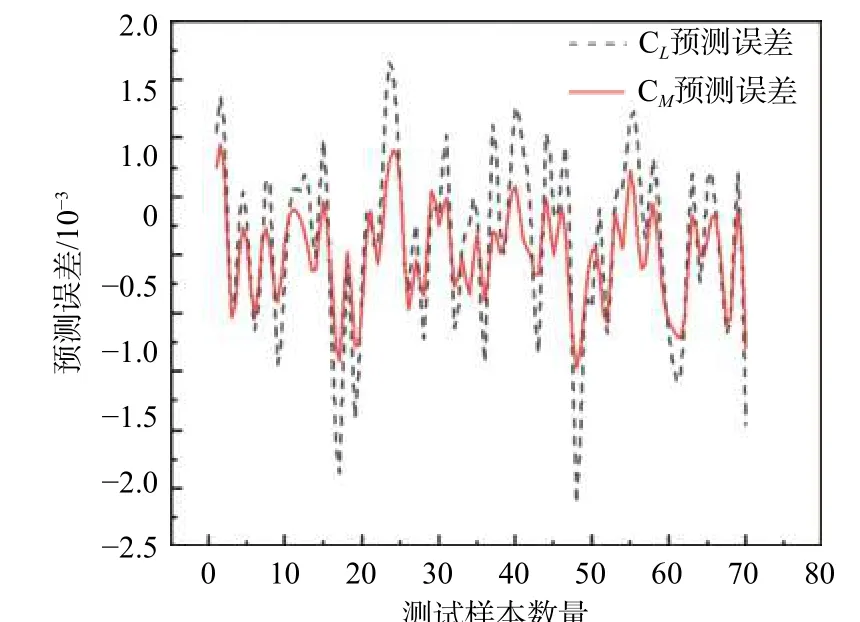
图8 预测误差曲线Fig.8 Prediction error curve

3.3 模型性能测试

本文目的是建立一种对气动参数快速预测的模型，所以模型的计算效率是评价本模型的重要的指标之一。为了测试训练好的模型的计算效率，选择在相同的工作站上，分别统计基于第2 节提出的CFD 仿真方法的计算时间（假设迭代600 步收敛）和训练好的CNN 模型预测70 个测试集的时间。其中CFD 仿真计算一种工况需要20 min，所建立的CNN 模型计算70 个工况只需要0.11 s 左右。可以看出本文所建立的机翼气动参数快速预测模型大大提高了机翼气动参数的计算效率。

模型的稳定性也是衡量模型好坏的重要标准之一，为了验证本节训练结果是偶然还是必然的。本文设计了一种模型稳定性实验。为避免其他因素的影响，采用同一工作站，同一参数，相同训练数据，相同迭代次数对模型进行训练，并统计每次训练好的模型在测试集上的误差绝对值的平均值，将其作为模型稳定性的衡量标准。本文总共进行了5 次实验，为节约时间成本，每次实验迭代设置为1 000 步，其结果如图9 所示。可以看出，不管检测CL端口的输出值，还是CM端口的输出值，其平均误差都存在波动，但从数据上看，5 次计算的平均误差的数量级相同，所以可以认为建立的预测模型具有较好的稳定性。

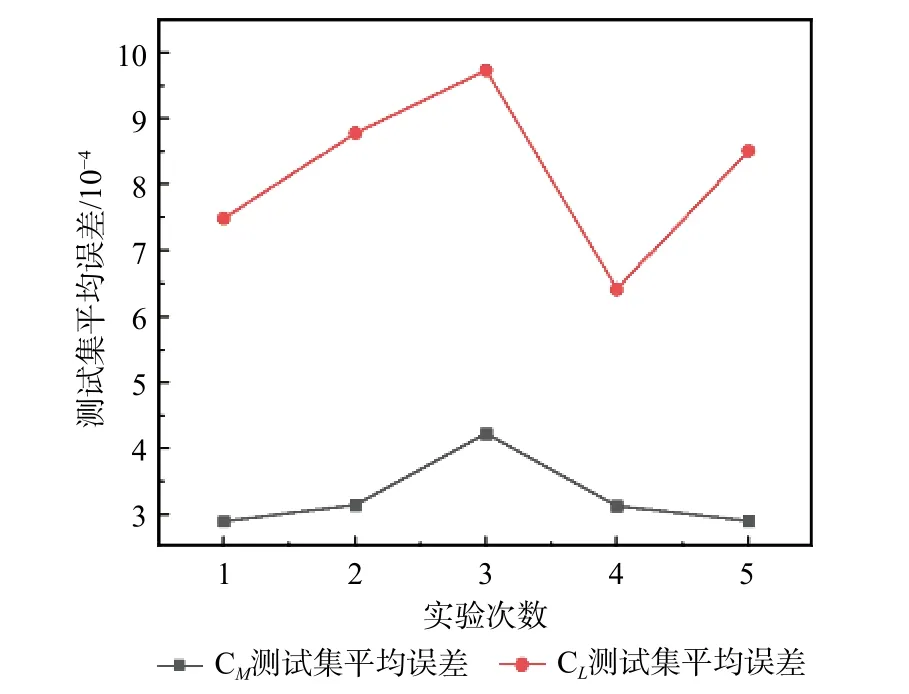
图9 测试集平均误差Fig.9 Average error of test set

4 结 论

1）基于卷积神经网络设计了一种快速预测机翼在不同攻角和浮沉状态下升阻力系数的模型，大大缩减了机翼气动参数计算的时间，为机翼颤振主动抑制研究提供了一种气动降阶模型。

2）通过实验证明了基于卷积神经网络建立的气动参数预测模型有很好的稳定性，同时，还发现可以通过减小模型的学习率和增大模型的迭代次数来进一步提高模型预测精度的稳定性。