基于M-AFSA 的MPRM 逻辑电路面积优化

邵艺璇，何振学，*，周宇豪，霍志胜，肖利民，王翔

(1.河北农业大学 河北省农业大数据重点实验室，保定 071001；2.河北农业大学 信息科学与技术学院，保定 071001；3.北京航空航天大学 计算机学院，北京 100191；4.北京航空航天大学 电子信息工程学院，北京 100191)

数字逻辑电路既可以采用基于“与/或/非”运算的传统布尔逻辑实现，也可以采用基于“与/异或”运算的Reed-Muller(RM)逻辑来实现。基于“与/异或”运算的RM 逻辑是区别于布尔逻辑的另一种电路表达方式。研究表明，与传统的布尔逻辑电路相比，利用RM 逻辑实现部分电路(如运算电路、奇偶校验电路等功能电路)具有更紧凑的结构和良好的可测性[1-3]。RM 逻辑分为混合极性RM（mixed polarity Reed-Muller, MPRM）逻辑和固定极 性RM（fixedpolarity Reed-Muller，FPRM）逻 辑。其中，MPRM 逻辑表达式是RM 逻辑中常见的一种规范表达形式。对于输入变量数为 n的Boolean 逻辑电路来说，具有2n个 固定极性，对应有2n个不同FPRM表达式；具有 3n个 不同的混合极性，对应有 3n个不同的MPRM 表达式。显然，对于同一电路来说，MPRM 逻辑比FPRM 逻辑具有更大的优化空间。

极性是RM 电路的重要属性，决定着RM 电路表达式的繁简，进而影响RM 电路的性能。MPRM电路面积优化是在极性优化空间中搜索对应某一/组电路性能最好的最佳极性。因此，MPRM 电路面积优化属于组合优化问题。对于中大规模MPRM 电路来说，其极性优化空间随输入变量数的增加呈指数型增长，穷尽搜索法无法在有限的时间内获得最优解。为满足中大规模MPRM 逻辑电路快速、有效搜索最佳极性的需求，需结合并行搜索能力更强、优化效率更高的智能优化算法。

智能优化算法在MPRM 电路面积优化领域得到了广泛应用。文献[4]将基于相异度的局部改善策略融入传统遗传算法，提出了一种基于混合遗传算法的MPRM 最小化算法，以避免算法陷于局部最优，增强了全局搜索能力。文献[5]将模拟退火算法与粒子群算法相结合提出一种模拟退火离散粒子群优化（simulated annealing and discrete particle swarm optimization , SADPSO)算法，基于该算法对MPRM 电路进行面积优化。文献[6]提出三值多样性粒子群算法并应用于MPRM 电路的综合优化，表现出了一定的性能优势。然而，由于受传统智能优化算法种群多样性差、收敛速度慢、易陷入局部最优等问题的影响，使得现有MPRM逻辑电路面积优化方法的优化效果有待提高。

人工鱼群算法(artificial fish swarms algorithm,AFSA)是一种全新的群智能优化算法，通过鱼群中人工鱼的觅食、聚群、追尾等行为以搜索全局最优解,具有鲁棒性强和全局寻优能力强等优点，在组合优化领域得到了广泛应用[7-14]。研究表明，在求解NP-Hard 优化问题上，人工鱼群算法效果明显优于遗传算法和粒子群算法[15-16]。

本文针对现有MPRM 电路面积优化效果差的问题，提出一种有效的MPRM 逻辑电路面积优化方法。与现有MPRM 电路面积优化方法相比，主要贡献如下：

1）提出一种多策略协同进化人工鱼群算法（multi-strategies artificial fish swarms algorithm, MAFSA），以用于求解三变量组合优化问题。该算法引入基于反向学习的种群初始化策略以提高了种群多样性及初始种群解的质量；引入提出觅食与追尾交互性策略，以加强人工鱼个体之间的信息交流提高收敛速度；引入自适应扰动策略，以增大算法进化后期人工鱼位置变异的随机性、避免陷入局部最优、增强算法的全局寻优能力。

2）提出一种MPRM 逻辑电路面积优化方法，该方法利用提出的M-AFSA 算法搜索电路面积最小的最佳极性。

3）基于北卡罗莱纳州微电子中心（Microelectronics Center of North Carolina, MCNC）Benchmark基准测试电路，所提算法分别与基于遗传算法（genetic algorithm，GA）的 面 积 优 化 方 法、基 于AFSA 的面积优化方法、文献[4]所提的混合遗传算法(hybrid genetic algorithm, HGA)及文献[17]中烟花进化人工鱼群算法（fireworks evolution AFSA,FEAFSA）的面积优化方法进行了实验对比，实验结果验证了所提算法的有效性。

一个输入变量数为n 的MPRM 逻辑电路中，对应的逻辑函数表达式具有 3n个不同的极性。若极性为 p，则该极性对应的MPRM 逻辑电路表达式可表示为

极性是MPRM 电路的重要属性，不同的极性对应着不同的MPRM 电路表达式。因此，极性决定着MPRM 电路表达式的繁简程度，进而影响MPRM电路的性能。

例1 以3 输入变量的Boolean 表达式f(x0,x1,x2)=x0x1x¯2+x¯0x1x¯2+x¯0x¯1x2为 例，其 对 应 极 性 为6（三 进制表示为020）、11（三进制表示为102）和17（三进制表示为122）的MPRM 电路表达式分别为

1 相关知识

1.1 MPRM 逻辑表达式

可以明显看出，不同极性对应的MPRM 表达式的繁简程度差别很大，其中，极性为17 的MPRM 电路表达式最简洁，具有潜在的功耗和面积等性能优势。

1.2 人工鱼群算法

人工鱼群算法由浙江大学李晓磊和钱积新[18]于2003 年提出，是一种全新的群智能优化算法。鱼个体数目最多的地方一般就是本水域中富含营养物质最多的地方，依据这一现象及鱼的特性，模仿鱼的觅食、聚群、追尾等行为，从而实现全局寻优。人工鱼的初始种群随机生成，人工鱼个体w=0,1,···,n-1；设种群规模为 popSize，pBest为个体最优值，gBest为全局最优值。人工鱼群算法对应的伪代码如下所示，其中，AF_follow()表示追尾行为，AF_swarm()表示聚群行为，AF_prey()表示觅食行为。

1.2.1 觅食行为

式中：prey(a)为人工鱼a 的觅食行为。

1.2.3 聚群行为

人工鱼游动过程中，会自然聚集成群。设人工鱼 Xc所在的位置是人工鱼群的中心位置，则人工鱼Xa向 Xc移动步长位置，否则进行觅食行为。人工鱼的位置更新为

2 多策略协同进化人工鱼群算法

传统人工鱼群算法的提出是为了解决连续型优化问题，并且在算法迭代后期，人工鱼搜索的盲目性较大，影响算法的收敛性及解的质量。由于MPRM 电路面积优化属于三值组合优化问题，所以本节基于人工鱼群算法提出M-AFSA。所提算法的主要创新点为：在种群初始化阶段加入反向学习机制，提出基于反向学习的种群初始化策略，以提高种群多样性及初始种群解的质量；为提高算法的收敛速度，提出觅食与追尾交互性策略，加强人工鱼个体之间的信息交流，避免因视野和步长为固定值，导致算法迭代次数过多；提出自适应扰动策略，增大算法迭代后期人工鱼位置变异的随机性，防止算法过早收敛，增强算法的全局寻优能力。

2.1 距离计算

例2 以5 输入变量为例，2 条人工鱼的位置分别为00 020、01 210，则2 条鱼之间的距离为3。

2.2 基于反向学习的种群初始化策略

初始种群的分布在一定程度上影响算法的收敛速度。为提高初始种群解的质量，提出基于反向学习的种群初始化策略，在随机初始化种群时，加入反向学习机制，保留最优个体，产生初始种群，以扩大种群多样性、提高初始种群解的质量、增强算法收敛性。

反向学习概念由学者Rahnamayan 等[19]提出，其主要目的是得到当前可行解的反向解，并对当前可行解及其反向解进行评估，选出最优解。该方法可有效提高种群多样性，增强群智能算法的全局寻优能力。

如果 d =0 且 f =1，则 s的反向解为

2.3 觅食与追尾交互性策略

在传统人工鱼群算法中，觅食行为是人工鱼不断地在视野范围内随机寻找其他较优位置，直至找到适应度值优于当前人工鱼的位置。因此，觅食行为可以使人工鱼更全面地搜索整个解空间。但该行为易使算法复杂度过高，影响算法的收敛速度。并且在该行为中，参数的设定对行为的性能有很大影响。参数设置过大，算法初期收敛速度很快，但易陷入局部最优；设置过小，会使算法的复杂程度过高，影响算法的运行效率。为解决该问题，更有效地平衡算法的开发和探索能力，本文在基于人工鱼群算法的基础上，对人工鱼群寻优策略进行了优化，在追尾、觅食阶段引入了觅食与追尾交互性策略。在追尾行为中，鱼群不断地向局部最优值移动，直至找到优于当前值的位置。在觅食行为中，鱼群不断地随机移动，直至找到优于当前值的位置。本文采用交互性追尾和觅食操作，让表现较好地个体执行先追尾后觅食的过程，以加快收敛速度。让表现较差的个体执行先觅食后追尾的过程，以跳出局部最优解，增强全局搜索能力。觅食与追尾交互性策略增加了鱼群间信息的交流，更有效地平衡算法的开发和探索能力。

2.4 自适应扰动策略

随着迭代次数的增加，人工鱼群算法的种群多样性降低，易使算法陷入局部最优。因此，在原有行为基础上引入遗传算法中的交叉和变异策略以提高种群多样性。当鱼群完成追尾和觅食行为之后对其实施扰动，以增加跳出局部最优解的概率，缩短寻找全局最优解的时间。概率过小，扰动行为会失去作用，不利于跳出局部最优解；概率过大，位置改变的随机性会偏大，破坏最优解收敛方向。因此，本文引入自适应扰动行为，随着迭代次数的增加，计算得出的概率值随之变化。迭代前期，扰动概率较小，加快收敛速度，迭代后期，扰动概率增大，增强算法跳出局部最优的能力。自适应扰动策略可增加人工鱼位置变异的随机性，防止人工鱼群算法过早收敛。自适应扰动策略的数学模型为

式中：gen 为迭代次数；α 和β 为固定常数，经过大量实验对比可得，α=2,β=0.3时，得到的实验数据最优。

2.5 算法描述

根据2.1 节～2.4 节所述，M-AFSA 流程如图1所示。

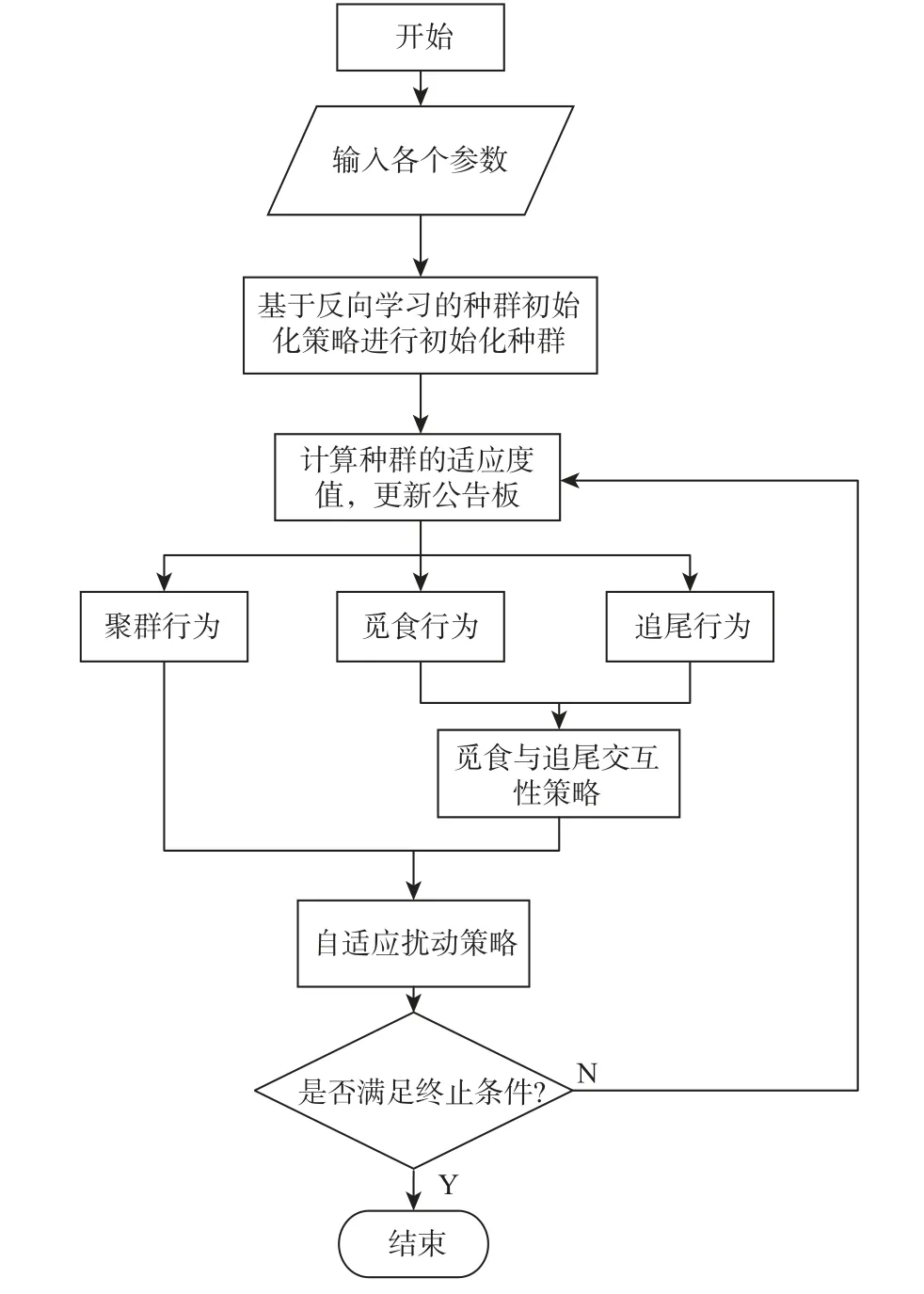
图1 M-AFSA 流程Fig.1 Flow chart of M-AFSA

具体步骤如下：

步骤 1 利用基于反向学习的种群初始化策略进行初始化种群。各项参数如下：N 为种群规模，visual 为人工鱼的视野范围，δ为人工鱼群的拥挤度因子，Try_num 为人工鱼移动的最大尝试次数，σ为自适应扰动策略中的扰动因子，T为当代迭代次数，Tmax为最大迭代次数。

步骤 2 公告板的初始化。比较初始种群的适应度值，将最优适应度值对应的人工鱼个体的位置赋值给公告板。

步骤 3 进行聚群行为，寻找当代种群的中心位置。若该位置的适应度值优于当前人工鱼的位置并且不拥挤，则向该位置方向移动，产生新的位置。

步骤 4 进行觅食与追尾交互性策略，判断个体适应度值。适应度值高的人工鱼个体执行先追尾后觅食的过程，适应度值低的人工鱼个体执行先觅食后追尾的过程。

步骤 5 计算扰动因子，若rand()＜ σ,则执行自适应扰动策略，否则进行下一步。

步骤6 判断算法是否满足终止条件，若满足，结束循环；否则，重复步骤3～步骤5。

2.6 时间复杂度分析

设M-AFSA 的种群规模为 N，迭代次数为Gen。

1）初始化种群阶段。由于引入反向学习概念，需要进行 2N 次操作，因此该阶段的时间复杂度为 O (2N)。

2）公告板的初始化阶段。进行 N次比较，找到初始种群的最优解，因此，该阶段的时间复杂度为 O (N)。

进行聚群行为与进行觅食与追尾交互性策略阶段。聚群行为中每个个体需要进行一次对比，一次移动，N次拥挤度计算。在觅食行为和追尾行为阶段，由于引入了觅食与追尾交互性策略，每个个体需要进行一次对比，一次移动，N次寻找视野范围内最优解，Try_num 次试探次数，因此，该阶段的时间复杂度为 O(2N+N2)+O(2N+N2+NTry_num)。

3）自适应扰动策略阶段。每个个体需要进行交叉操作一次，变异操作一次，因此，该阶段的时间复杂度为 O(2N)。

因此，M-AFSA 在Gen 次迭代后的时间复杂度为O(2N)+O(Gen(2N2+7N+NTry_num))。

2.7 空间复杂度分析

M-AFSA 中人工鱼群的种群规模为 N，在算法运行过程中，需要 N 个结构体 A_fish存储人工鱼的各项参数及长度为 l的一维数组，所需的空间为Nl；需要一个结构体存储种群最优解，所需空间为l。因此，该算法需要的存储空间为O(Nl + l)。

3 MPRM 逻辑电路面积优化方法

MPRM 电路极性优化空间随电路输入数的增加呈指数型增长。较小规模的电路面积优化可以通过穷尽搜索方法实现，但是对于中大规模MPRM逻辑电路的面积优化，穷尽搜索方法无法在有限的时间内得到最优解。为满足中大规模MPRM 逻辑电路快速、有效面积优化的需要，本文提出一种MPRM 逻辑电路面积优化方法，该方法利用MAFSA 搜索电路面积最小的最佳极性，从而实现电路面积优化。

3.1 编码方案

人工鱼的位置表示MPRM 逻辑电路中的极性，通过三进制编码，将极性的三进制形式表示人工鱼个体所在的位置。

例3 以5 输入变量的电路为例：极性为6 的三进制表示为00020，则代表该极性的人工鱼的位置为00020。

3.2 面积估算模型

适应度值越高，则人工鱼个体的质量越好。因此，将面积计算函数的倒数作为适应度函数：

3.3 适应度函数

式中：finess(w)为 个体 w 的适应度值；Area(w)为个体w的电路面积。

3.4 MPRM 逻辑电路面积优化方法描述

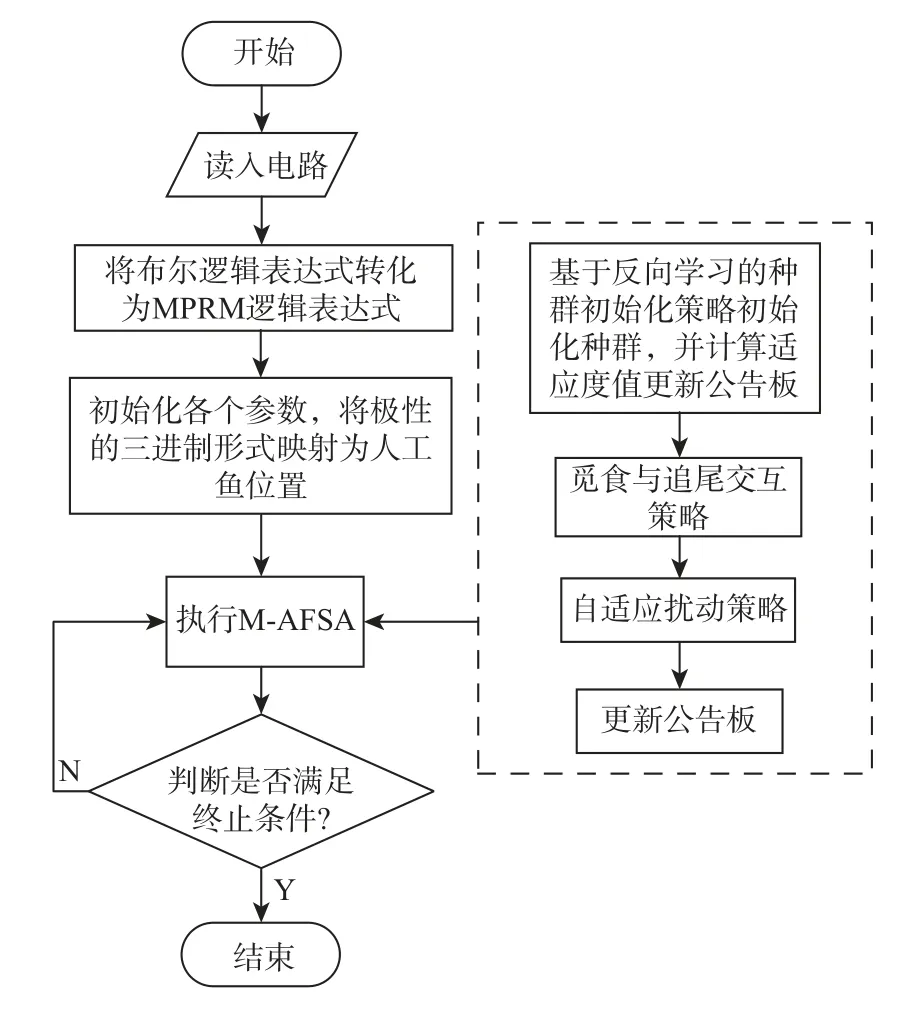
图2 MPRM 电路面积优化方法流程Fig.2 Flow chart of MPRM circuit area optimization method

逻辑表达式；然后，通过三进制编码方式对人工鱼的位置进行编码，并利用汉明距离表示人工鱼之间的距离；最后，通过M-AFSA 搜索电路面积最小的最佳极性。

4 实验结果与分析

本文所提方法使用C 语言实现，软件环境为：Windows 10操作系统、VS 2019 编译器，硬 件 环 境 为：Intel (R) Core (TM)i5-10210U CPU (2.11GHZ) 8GB RAM。测试电路为MCNC Benchmark 基准电路。

为了验证所提方法的有效性，将所提算法与GA、AFSA、文献[4]所提的HGA 及文献[17]所提的FEAFSA 进行比较。从MCNC Benchmark 基准电路测试集中随机选取11 个电路作为实验电路,其中，输入变量个数为5～8 的为小规模电路，输入变量个数为9～17 的为中大规模电路。由于5 种算法都具有随机性，本实验将每个算法在每个测试电路上运行20 次，并将实验结果的最优值和平均值作为实验数据。

4.1 电路面积对比

5 种算法的电路面积优化对比数据如表1、表2 所示，其中MCNC 表示电路名称，为验证所提方法的有效性，从小、中、大规模电路中，各随机选取若干电路，In 表示测试电路的输入变量个数，A_ave 表示20 次运行中求得的电路面积的平均值，T_ave 表示对应的平均时间。S1、S2、S3、S4分别表示 M-AFSA 与 GA、HGA、AFSA 及 FEAFSA相比较，所优化的最小面积百分比；S5、S6、S7、S8分别表示M-AFSA 与GA、HGA、AFSA 及FEAFSA比较，所优化的面积平均值百分比。

表1 中数据为5 种算法求得的电路的最小面积，表2 中数据为5 种算法求得的电路的平均面积以及对应的平均时间。由表1 可知，对于小规模电路来说，5 种算法得到的最小面积一致，但是M-AFSA得到的电路面积的平均值要优于其他4 种算法。对于中大规模电路来说，M-AFSA 得到的最小面积优于其他4 种算法，且平均值明显优于其他4 种算法。M-AFSA 比GA 在平均面积上最高节省了57.24%、平均节省了39.57%；M-AFSA 比HGA 在平均面积上最高节省了19.74%、平均节省了2.06%；比AFSA 在平均面积上最高节省了33.53%、平均节省了14.54%；比FEAFSA 在平均面积上最高节省了30.25%、平均节省了13.86%。

表1 最优面积数据Table 1 Optimal area data

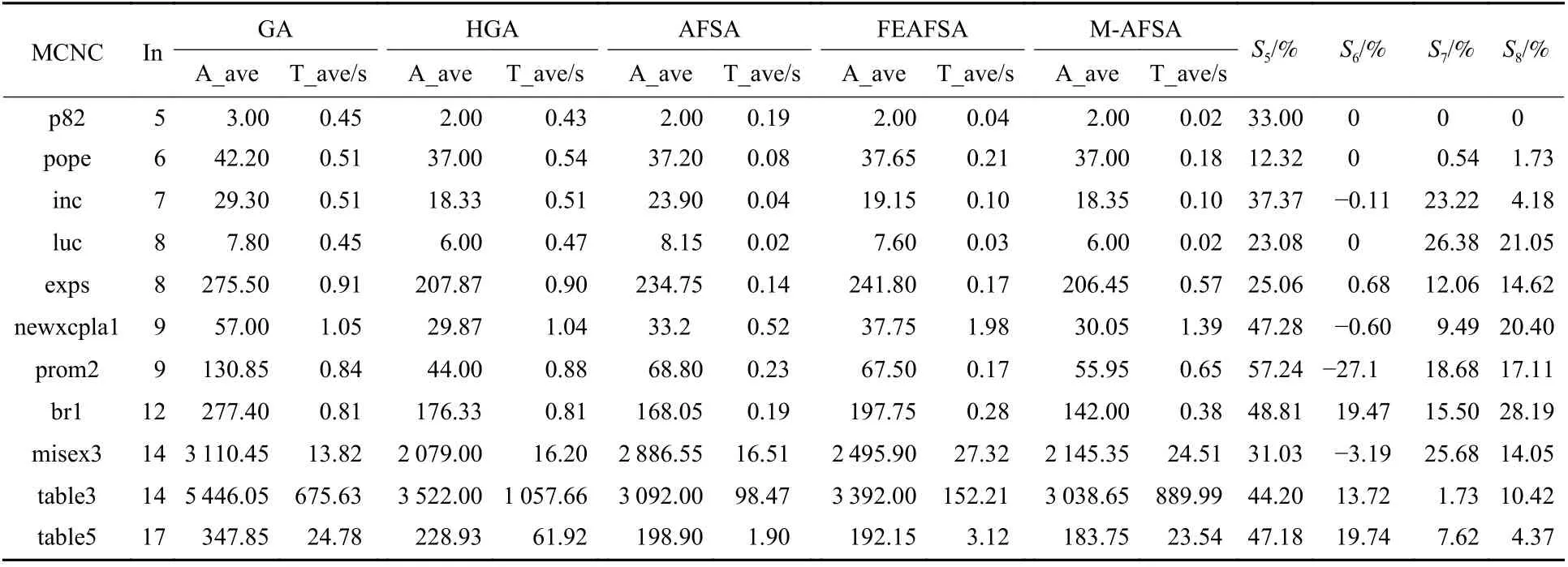
表2 平均面积与平均时间数据Table 2 Average area and average time data

4.2 收敛性对比

为验证M-AFSA 算法的收敛性，随机选取8 个MCNC Benchmark 基准电路。4 种算法的收敛性如图3 所示，其中，横坐标为迭代次数，纵坐标为运行20 次测试电路面积的平均值。可以看出，与GA、AFSA 及FEAFSA 相比，M-AFSA 能够 在迭代次 数最小的情况下，找到最小面积。

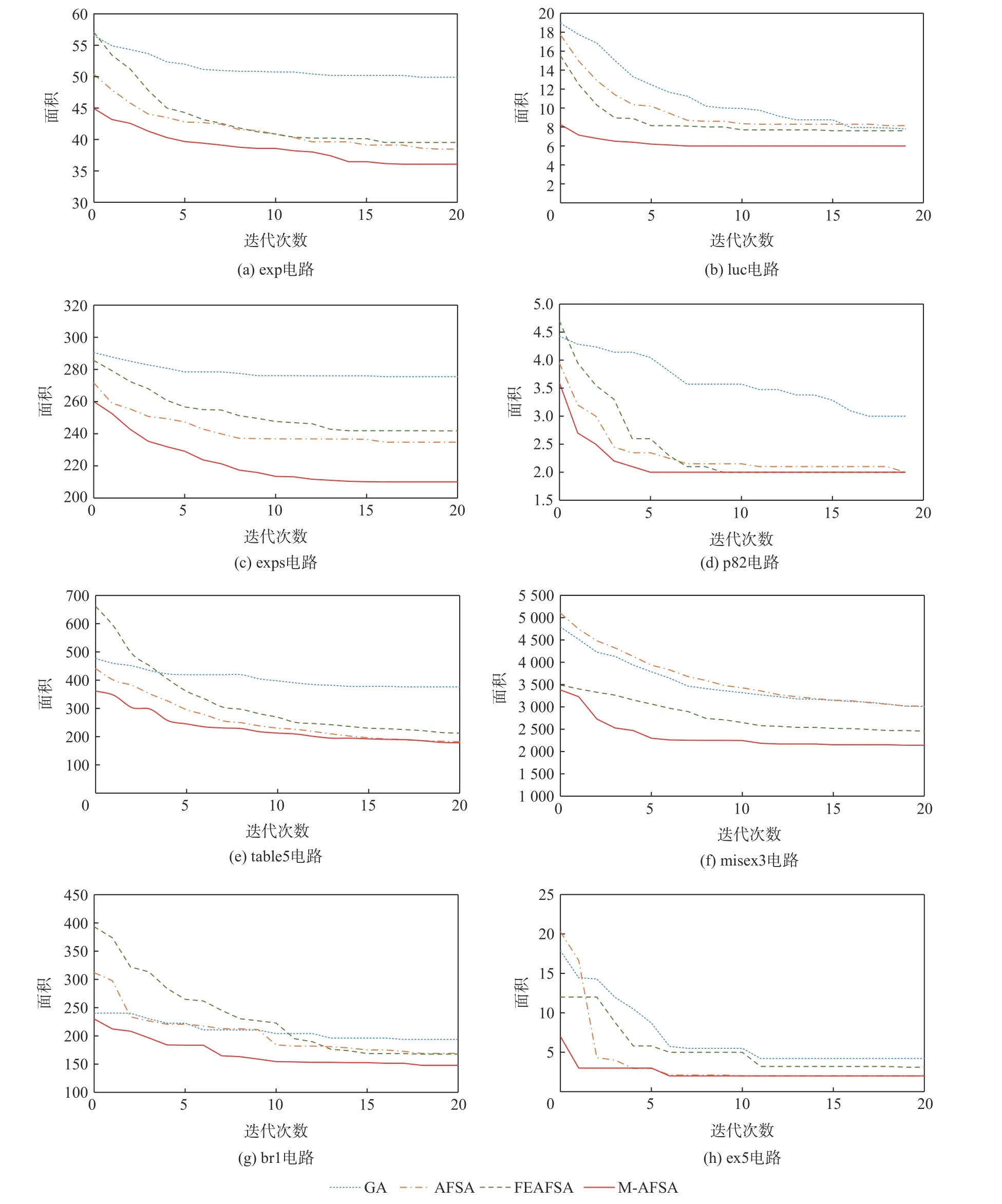
图3 8 种基准电路最小面积优化曲线Fig.3 Optimization curves of minimum area of eight reference circuit

从图3 中可以直观地看出，通过基于反向学习的种群初始化产生的初始种群的平均面积，均小于其他对比算法，验证了基于反向学习的种群初始化策略的有效性；此外，由M-AFSA 曲线与AFSA 曲线相比，可看出M-AFSA 收敛速度快，验证了觅食与追尾交互性策略可有效地提高算法的收敛速度；最后，从图3 中可看出M-AFSA 找到的面积绝大多数小于其他3 种算法，验证了自适应扰动策略可有效地避免M-AFSA 陷入局部最优。

5 结 论

本文所提算法用于解决MPRM 电路面积优化问题。主要结论如下:

1）提出的M-AFSA 在初始化种群方面加入反向学习机制，提高了种群的多样性、初始种群解的质量和算法的收敛速度；M-AFSA 在追尾和觅食这2 种基本行为中加入觅食与追尾交互性策略，增加个体之间的信息交流，提高局部搜索能力，加快算法的收敛速度；传统人工鱼算法随着迭代次数的增加，人工鱼群算法的种群多样性降低，为改善这一缺点，M-AFSA 加入自适应扰动策略，增加人工鱼的位置变异随机性，防止人工鱼群算法过早收敛。

2）提出一种MPRM 电路面积优化方法，该方法利用M-AFSA 来搜索MPRM 逻辑电路面积的最优解。

3）通过大量MCNC 测试电路的实验结果可表明,M-AFSA 在MPRM 逻辑电路优化方面具有较好的收敛性和寻优性能。基于MCNC Benchmark 电路的实验结果表明，与GA 相比，所提算法优化电路平均面积百分比最高为57.24%；与HGA 相比，所提算法优化电路平均面积百分比最高为19.74%；与AFSA 相比，所提算法优化电路平均面积百分比最高为33.53%；与FEAFSA 相比，所提算法优化电路平均面积百分比最高为30.25%。