函数构题 抓住本质 重在审题

刘玉晶

一次函数是初中所学函数部分最为基础且非常重要的一个类型，在中考命题中占据了一定的分量. 其中考的考点主要集中在一次函数的定義、图象性质、求解析式，与不等式和方程的结合，最终落脚点为一次函数的实际应用.主要采用以函数为主线，将函数图象、性质、方程及不等式等相关知识综合运用，利用数形结合的思想解决相应的实际问题.

考点分析

考点1：一次函数图象及性质、确定一次函数的解析式

解题思路：首先要理解题意并观察图象，从中获取信息，正确理解自变量和函数所代表的实际意义，并且要常常进行“数”与“形”之间的互换，如函数图象如何转化为函数解析式；然后利用一次函数图象及性质、解析式等知识解决问题，从而将问题转化为方程与函数问题，这里涉及函数、方程的综合运用.

易错点：对自变量或者函数所代表的实际意义理解不准确；忽视一次函数图象的性质.

解题要点：掌握一次函数图象及性质是解决这类题型的基础.解题时要读懂题意，理顺关系，要全面分析关系，领悟实质，即良好的审题能力和读图能力以及处理和转化条件的能力也是解决一次函数图象应用题的重要因素.

考点2：利用一次函数、方程、不等式等知识解决现实生活中的优惠方案问题

解题思路：解这类题，需要在了解实际问题中各个量关系的基础上，先确定一次函数的解析式，然后找到相关的信息建立与方程或不等式的联系，计算出可能的方案选项，然后根据一次函数的增减性确定解决方案.

易错点：忽略不等式模型的建立；没有注意到自变量的限制条件.

解题要点：首先要根据题目中的条件列出解析式，其次通过分析题意找出自变量的取值范围，再次根据一次函数的增减性及取值范围，确定自变量的值，作出决策，最后把数学结果回归到实际问题中去，通过分析、判断、验证得到实际问题的结果.注意：回归时要利用实际意义的条件进行检验取舍，找出正确结果.

真题分析

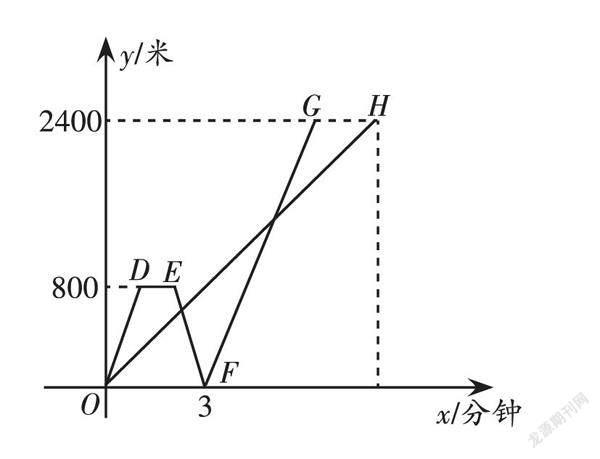
例1 （2022·黑龙江·牡丹江）在一条平坦笔直的道路上依次有A，B，C三地，甲从B地骑电瓶车到C地，同时乙从B地骑摩托车到A地，到达A地后因故停留1分钟，然后立即掉头（掉头时间忽略不计）按原路原速前往C地，结果乙比甲早2分钟到达C地，两人均匀速运动，图1是两人距B地路程y（米）与时间x（分钟）之间的函数图象．请解答下列问题：

（1）填空：甲的速度为______米/分钟，乙的速度为______米/分钟；

（2）求图象中线段FG所在直线表示的y（米）与时间x（分钟）之间的函数解析式，并写出自变量x的取值范围；

（3）出发多少分钟后，甲、乙两人之间的路程相距600米？请直接写出答案．

解析：（1）利用速度 = 路程 ÷ 时间，找准甲、乙的路程和时间即可得出结论.答案：300；800.

（2）根据（1）中的计算可得出点G的坐标，设直线FG的解析式为：y = kx + b，将F，G的坐标代入，求解方程组即可.直线FG的解析式为：y = 800x - 2400（3 ≤ x ≤ 6）.

（3）根据题意可知存在三种情况，然后分别计算即可．

当0 ≤ x ≤ 1时，甲从B地骑电瓶车到C地，同时乙从B地骑摩托车到A地；

当2 ≤ x ≤ 3时，甲从B地继续往C地走，乙从A地往B地走；

当x > 3时，甲从B继续往C地走，乙从B地往C地走.

综上，出发[6/11]分钟或[18/5]分钟或6分钟后，甲、乙两人之间的路程相距600米．

例2 （2022·山东·济宁）某运输公司安排甲、乙两种货车24辆恰好一次性将328吨的物资运往A，B两地，两种货车载重量及到A，B两地的运输成本如下表：

（1）求甲、乙两种货车各用了多少辆.

（2）如果前往A地的甲、乙两种货车共12辆，所运物资不少于160吨，其余货车将剩余物资运往B地．设甲、乙两种货车到A，B两地的总运输成本为w元，前往A地的甲种货车为t辆．

①写出w与t之间的函数解析式；

②当t为何值时，w最小？最小值是多少？

解析：（1）设甲种货车用了x辆，可得：16x + 12（24 - x） = 328，即可解得甲种货车用了10辆，乙种货车用了14辆.

（2）①根据题意得：w = 1200t + 1000（12 - t） + 900（10 - t） + 750[14 - （12 - t）] = 50t + 22 500；

②根据前往A地的甲、乙两种货车共12辆，所运物资不少于160吨，可得4 ≤ t ≤ 10，由一次函数性质可得当t为4时，w最小，最小值是22 700元．

总结提升

方法提炼：

1.用一次函数解决实际问题的一般步骤为：

（1）根据题意，设定问题中的变量；

（2）建立一次函数关系式模型；

（3）利用与方程或不等式（组）的知识，结合实际问题，确定自变量的取值范围；

（4）利用一次函数的性质来解决实际问题

2.用待定系数法求一次函数的解析式：

已知两点A（x1，y2），B（x2，y2）（x1 ≠ x₂），求直线AB的解析式.

注意：利用[k=y1-y2x1-x2]可快速求出k的值.

专题精练

某商店决定购进A、B两种北京冬奥会纪念品. 若购进A种纪念品10件，B种纪念品5件，需要1000元；若购进A种纪念品5件，B种纪念品3件，需要550元．

（1）求购进A、B两种纪念品的单价.

（2）若该商店决定拿出1万元全部用来购进这两种纪念品，考虑到市场需求，要求购进A种纪念品的数量不少于B种纪念品数量的6倍，且购进B种纪念品数量不少于20件，那么该商店共有几种进货方案？

（3）若销售每件A种纪念品可获利润20元，每件B种纪念品可获利润30元，在第（2）问的各种进货方案中，哪一种方案获利最大？求出最大利润．

答案：（1）25元，150元；（2）5种；（3）购进A种纪念品226件，B种纪念品29件获利最大，最大利润为5390元.