“一边一角”的构造

栾长伟

“图形与几何”作为初中数学四大领域之一，在整个初中学习过程中占较大比例，对培养同学们的合情推理与演绎推理至关重要. 其中，添加适当的輔助线构造全等在2022年全国各地中考试卷频繁出现，下面介绍使用“一边一角”构造全等的基本方法.

[考点提炼]

考点1：存在一组边相等，这组边上有一组相等的角，我们称之为“一边一等角”. 解题时常把这一组等边和等角放在一个三角形中，去构造另外一个三角形与之全等，常见的构造方法有“SAS”和“AAS”

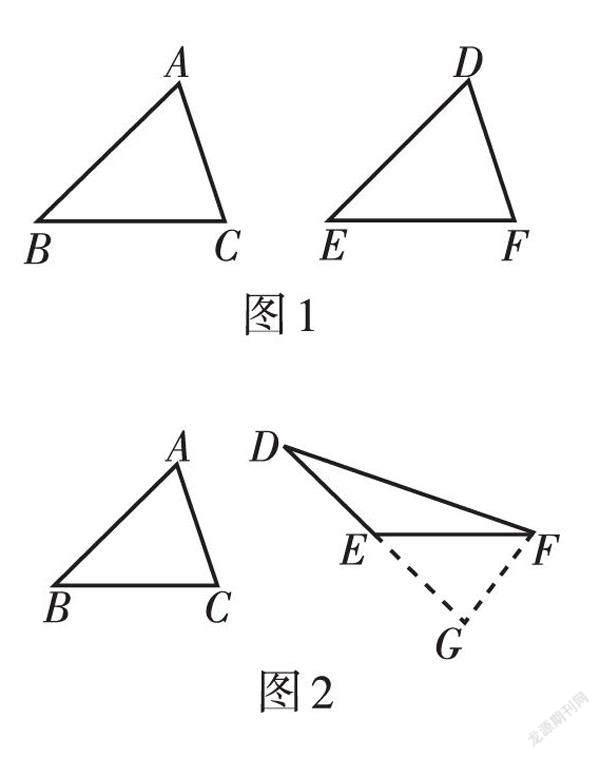
解题思路：如图1，若“BC = EF，∠B = ∠E”，则满足“一边一等角”条件，此时我们先把BC和∠B放到△ABC中，作DE = BA或者∠F = ∠C，则可以得到△DEF≌△ABC.

易错点：不是所有的三角形都适用，要根据具体问题具体分析.另外，从尺规作图角度考虑，在构造全等时，我们不去作∠D = ∠A，只作相等边另一端的两个角相等.

解题要点：首先确定是否满足“一边一等角”的条件，若满足，则将这“一边一等角”放入一个三角形中，再去构造另外一个三角形与之全等，从而再利用全等得到的结论解决问题.

考点2：存在一组边相等，这组边上有一组互补的角，我们称之为“一边一补角”.解题时先将其中一个角的补角构造出来，转化为“一边一等角”解决问题

解题思路：如图2，若“BC = EF，∠B + ∠DEF = 180°”，则满足“一边一补角”条件，此时我们先延长DE，再把BC和∠B放到△ABC中，作EG = BA或者∠EFG = ∠C，则可以得到△EFG≌△BCA.

易错点：构造一角的补角就是反向延长这个角的两条边，共有两种延长方法，但是只有一种是可行的，即延长后得到的相等的角的一边是已知等边.

解题要点：关键在于将“一边一补角”转化为“一边一等角”，即选择合适的作补角的方式.

[真题精讲]

例1 （2022·辽宁·大连）综合与实践.

问题情境：数学活动课上，王老师出示了一个问题：

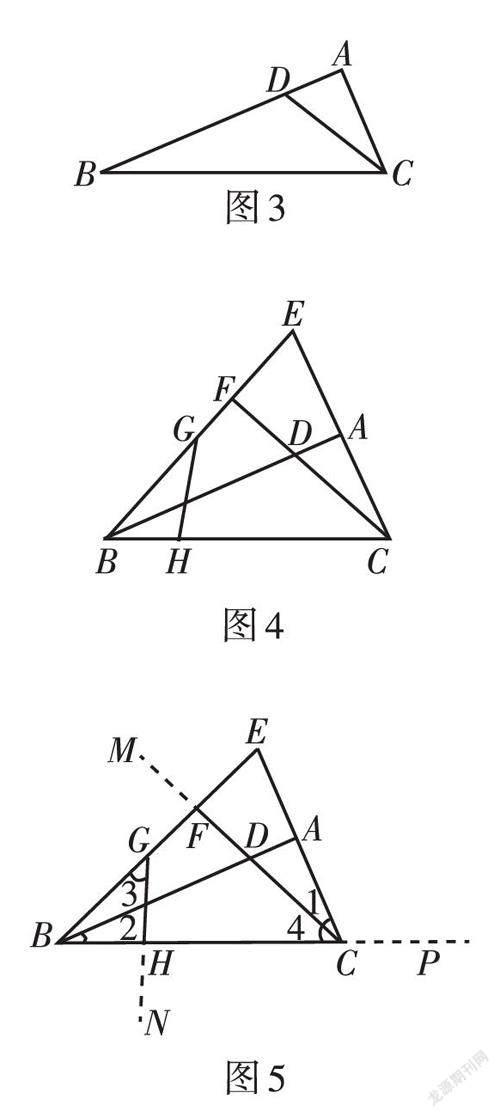
如图3，在△ABC中，D是AB上一点，∠ADC = ∠ACB. 求证∠ACD = ∠ABC．

独立思考：（1）请解答王老师提出的问题．

实践探究：（2）在原有问题条件不变的情况下，王老师增加下面的条件，并提出新问题，请你解答.

如图2，延长CA至点E，使CE = BD，BE与CD的延长线相交于点F，点G，H分别在BF，BC上，BG = CD，∠BGH = ∠BCF. 在图中找出与BH相等的线段，并证明．

第二问思路分析：

1.本题中有三组等边：CE = BD，BG = CD，BH = EF（待证）；

2.直接可用的两组等角，如图5，∠1 = ∠2，∠3 = ∠4，与已知两组等边分别构成“一边一角”形；

3.由∠3 = ∠4，可以进一步得到一个对角互补的四边形FGHC，进而可以得到两组等角，与待证BH = EF构成“一边一角”形.

4.由∠ADC = ∠ACB，还可以得到∠BDC = ∠ECP，与CE = BD构成“一边一角”形.

5.综合以上条件不难发现，此题满足全等证明方法“一边一角”的条件.

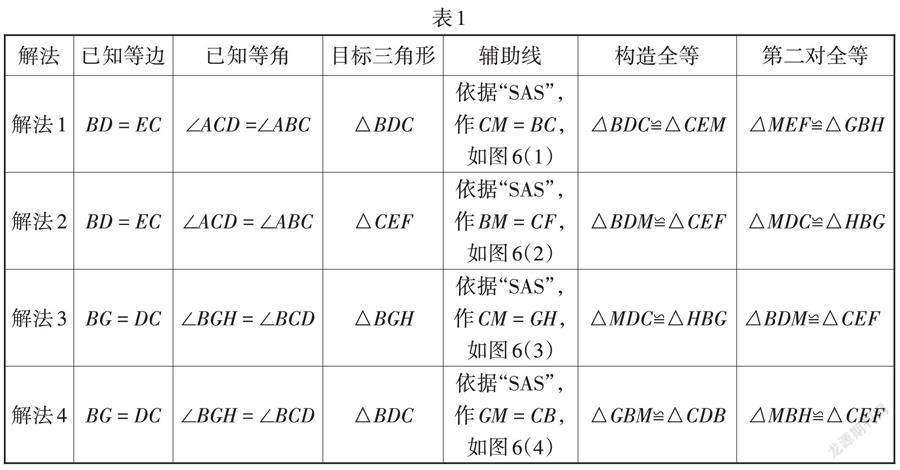
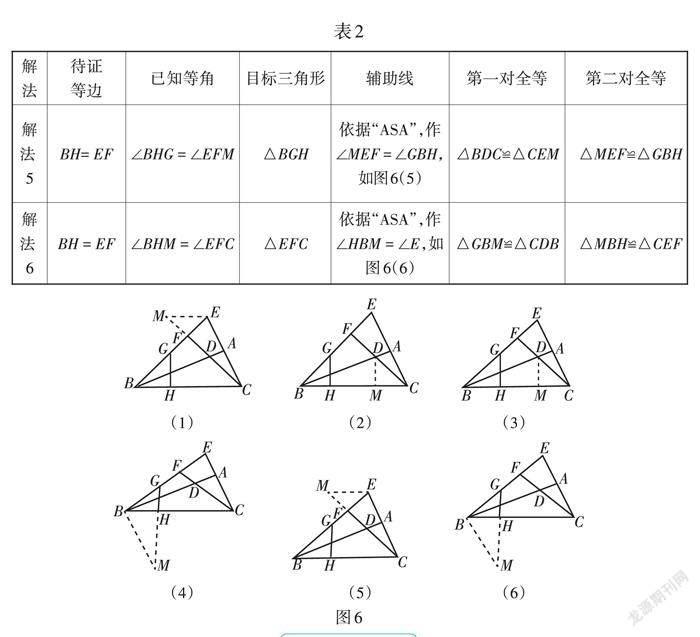
解题方法呈现（如表1、表2）：

[总结提升]

中考几何试题的核心是通过添加辅助线构造全等，基本上分为两类，一类是变换，另一类就是“一边一角”构造，其中后者更为常见. 在“一边一角”的应用过程中，解题关键是选择适合的三角形. 我们要本着可以“转化”所求为目的，即通过全等构造能使已知条件或者所求结论进行转化，这就是“一边一角”构造的核心所在.

[专题精练]

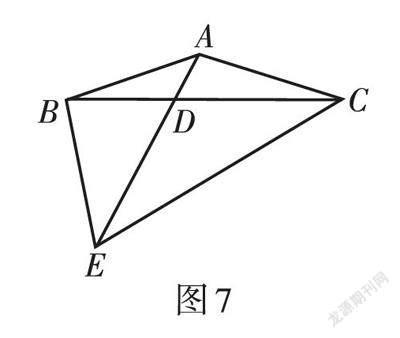
例2 如图7，在△ABC中，D是BC上一点，点E在AD的延长线上，BE = AC，∠CED = ∠DBE - ∠ACE， 写出图中与DE相等的线段并说明理由.

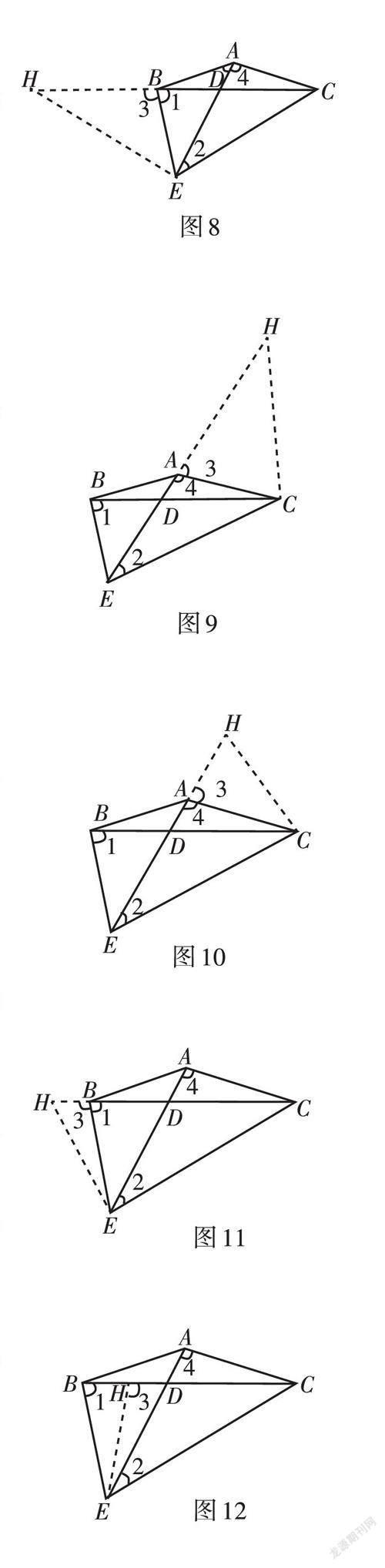
解法1：已知一边（BE = AC） + 一角（∠3 = ∠4） + 目标△AEC. 如图8，在CB延长线上截取BH = AE，

∵∠1 = ∠ACE + ∠2，∠1 + ∠3 = 180°，

∠ACE + ∠2 + ∠4 = 180°，

∴∠3 = ∠4，∴△BEH ≌ △ACE，∴EH = CE，∠H = ∠2，

∴∠H = ∠BCE，∴∠2 = ∠BCE，∴DE = CD.

解法2：已知一边（BE = AC） + 一角（∠1 = ∠3） + 目标△BCE.

如图9，在EA延长线上截取AH = BC，

∵∠1 = ∠ACE + ∠2，∠4 + ∠3 = 180°，

∠ACE + ∠2 + ∠4 = 180°，

∴∠1 = ∠3，∴△BEC≌△ACH，∴CE = CH，∠H = ∠BCE，

∴∠H = ∠2，∴∠2 = ∠BCE，∴ED = CD.

解法3：已知一边（BE = AC） + 一角（∠1 = ∠3） + 目标△BED.

如图10，在EA延长线上截取AH = BD，

∵∠1 = ∠ACE + ∠2，∠4 + ∠3 = 180°，

∠ACE + ∠2 + ∠4 = 180°，

∴∠1 = ∠3，∴△BED≌△ACH，

∴ED = CH，∠H = ∠BDE，

∴∠H = ∠HDC，∴CD = CH，∴DE = CD.

解法4：已知一边（BE = AC） + 一角（∠3 = ∠4） + 目标△ACD.

如图11，在CB延长线上截取BH = AD，

∵∠1 = ∠ACE + ∠2，∠1 + ∠3 = 180°，

∠ACE + ∠2 + ∠4 = 180°.

∴∠4 = ∠3，∴△ACD ≌ △BEH，∴HE = CD，∠H = ∠ADC，

∴∠H = ∠HDE，∴HE = ED，∴DE = CD.

解法5：已知一边（BD = CD） + 一角（∠EDH = ∠CDA） + 目标△ACD.

如图12，以E为圆心，EB为半径画弧交BC于点H，连接EH，

∴∠1 = ∠BHE，BE = HE = AC，

∵∠1 = ∠ACE + ∠2，∠1 + ∠3 = 180°，∠ACE + ∠2 + ∠4 = 180°，

∴∠4 = ∠3，∴△ADC≌△HDE，∴DE = CD.