柔性间隙影响下涡旋压缩机主轴系统动力学特性研究*

邱海飞

（西京学院机械工程学院 陕西西安 710123）

涡旋压缩机是一种利用容积变化来实现气体压缩的高速旋转机械， 相对于其他类型压缩机（如轴流式、 离心式和混流式压缩机等）， 涡旋压缩机具有高速、 高效、 低振和低噪等诸多优点， 目前已被广泛应用于空调制冷、 石油化工、 交通运输及动力工程等领域[1］。 主轴部件是涡旋压缩机系统的心脏， 在实际当中， 由于受到制造装配误差、 零部件磨损及材料变形等因素影响， 主轴系统内部将不可避免地存在运动副间隙[2］， 由此引发的回转偏离、 冲击碰撞或振动噪声等， 会对涡旋压缩机的稳定运行产生不利影响。 因此， 在对涡旋压缩机系统进行动平衡设计时， 必须综合考虑工作转速、 轴承精度及运动副间隙等因素， 以尽可能提高主轴系统的运转效能。

在含间隙涡旋压缩机主轴系统研究方面， 已有学者进行了一系列探索。 赵嫚等人[3］建立了某卧式涡旋压缩机的转子动力学模型， 并在气体力作用下对其进行仿真分析， 获得了运动副在不同间隙下的接触力和运动参数。 王训杰和薛丽[4］针对涡旋压缩机的泄漏问题， 在不同径向间隙下对其内腔流场进行了数值模拟， 并指出控制径向间隙有助于改善动涡盘受力不均、 提高容积效率。 黄华军等[5］建立了基于非线性等效弹簧阻尼和库仑摩擦的涡旋压缩机动力学模型， 分别对小轴防自转机构、 间隙大小和间隙数目3 种情况进行了动力学仿真， 为选择合理的轴承游隙设计提供了借鉴。 万赫男[6］利用Minitab 蒙特卡洛法对涡旋压缩机轴向间隙进行了模拟分析， 并根据尺寸链计算和轴向间隙统计数据实现了尺寸偏差优化。

然而， 以往针对涡旋压缩机的间隙计算和仿真研究， 大多都停留在刚体动力学层面， 没有考虑主轴系统的弹性变形和应力影响， 所以不能精确反映由运动副间隙引发的微幅振动和接触变形， 不利于分析和理解含间隙主轴系统的复杂力学机制。 因此， 本文作者以某卧式涡旋压缩机主轴系统为例， 在不同轴承间隙下实现了主轴系统的动力学建模和柔性接触仿真， 研究结果对于含间隙涡旋压缩机的优化设计具有一定参考价值。

1 涡旋压缩机主轴结构及原理

为使涡旋压缩机能够顺利进行吸气、 压缩和排气作业， 要求动涡盘与静涡盘之间必须形成多个月牙形封闭容积腔[7］， 因此涡旋压缩机主轴一般都采用偏心结构， 如图1 所示。 为了消除惯性离心力影响， 需要在偏心主轴上配装一定质量的负重， 即大小平衡铁；十字滑环安装在动涡盘与机架之间， 主要作用是防止动涡盘发生自转； 静涡盘通过刚性联接与机架固为一体， 在主轴系统转动过程中始终处于静止状态。

涡旋压缩机启动运行后， 电动机扭矩通过皮带传动输入至主轴系统， 随着偏心主轴的高速回转， 动涡盘在曲拐和十字滑环作用下绕主轴中心线作圆周轨迹平动[8］。 与此同时， 动涡齿与静涡齿发生周期性啮合， 并在机体内部形成多个连续变化的月牙形封闭容积腔， 最后通过容积变化来实现气体的持续吸入、 压缩和排放。

2 间隙运动副动力学建模

2.1 间隙矢量模型

运动副间隙普遍存在于各类工程机械， 不含间隙的运动副是一种理想状态， 因此， 对于实际当中的机械传动系统而言， 运动副间隙是不可避免的[9］。 由轴销和轴套构成的间隙旋转副如图2 所示， 当轴销与轴套因间隙影响而不相互接触时， 可按式（1） 计算旋转副间隙半径r。 式中：R1为轴销半径，R2为轴套内半径。 在理想状态下， 间隙半径r＝0， 此时轴销与轴套完全接触， 且在接触表面存在弹性和阻尼。

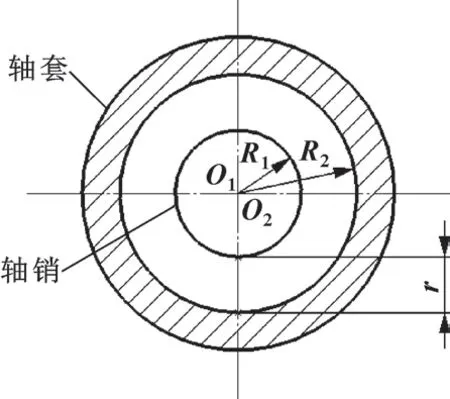
图2 运动副间隙结构示意Fig.2 Structure of joint clearance

在轴与轴承装配形成的旋转副中， 设轴回转中心O1的坐标为（x1，y1）， 轴承回转中心O2的坐标为（x2，y2）， 当轴与轴承处于接触状态时， 建立如图3所示运动副间隙矢量模型。 分析几何条件可知， 当中心距O1O2小于间隙圆半径r时， 轴与轴承之间不存在接触， 如式（2） 所示， 表示旋转副为含间隙自由状态[10］。 反之， 当O1O2≥r时， 则表示轴与轴承发生接触或表面形变， 此时O1O2与x轴的夹角φ称之为接触角， 如式（3） 所示。 由此可见， 旋转副处于间隙或是接触状态， 完全取决于轴和轴承回转中心O1、O2的位置。

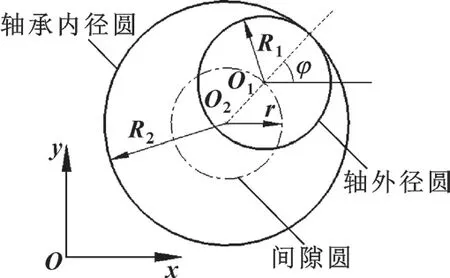
图3 运动副间隙矢量模型Fig.3 Vector model of joint clearance

2.2 接触碰撞力模型

含间隙运动副的接触碰撞过程存在随机性， 总体可归结为“自由运动-接触变形” 两种状态。 相对于其他间隙模型（如连续接触模型、 多状态非连续接触模型）， 这种两状态非连续接触模型综合考虑了接触表面的弹性和阻尼及摩擦等因素， 所以能够更为准确和真实地表征碰撞过程[11］。

以运动副间隙矢量模型为依据， 将两状态间隙副应用于涡旋压缩机主轴系统， 在曲柄销与轴承之间构建非连续接触碰撞模型， 其广义形式如式（4） 所示。

式中：Fn为法向接触力；K为等效接触刚度；C1、C2为阻尼因子；δ为法向穿透深度；为接触点碰撞速度；n为≥1 的力指数（与材料种类相关）。

2.3 间隙摩擦力模型

由于存在运动副间隙， 使得主轴系统会受到铰间摩擦阻力矩影响。 为了更为准确地描述主轴系统的动力学特性， 必须考虑曲柄销与滚针轴承之间的切向摩擦力[12］， 而经典的库仑（Coulomb） 摩擦力模型由于没有将切向速度分量考虑在内， 所以无法准确分析当切向速度为0 时的摩擦力真实状态。 因此， 文中采用修正的Coulomb 摩擦模型描述间隙运动副的切向接触特性， 如式（5） 所示， 为修正后的切向摩擦力Ft的计算公式[13］。

式中：μf为动摩擦因数；cd为动态修正系数；vt为相对切向速度；Fn为法向接触力。

3 柔性间隙接触仿真

3.1 动力学方程

柔性化建模是在结构离散的基础上对原有刚性体进行替代， 即通过有限的单元节点来近似逼近实体的无限自由度[14］， 进而更为准确地表征机械系统的动力学特性。 广义坐标下的柔性体运动微分方程如式（6） 所示， 该方程通过模态向量和模态坐标的线性组合来描述构件的弹性位移。

式中：Q为广义作用力；ξ为广义坐标；M为柔性体质量矩阵；D为模态阻尼矩阵；K为广义刚度矩阵；ψ为约束方程；λ为拉格朗日因子；fg为广义重力。

3.2 刚柔耦合建模

通过CREO 数据接口转化， 将涡旋压缩机三维CAD 实体模型送入ADAMS／View。 根据涡旋压缩机结构组成与传动关系， 配置主轴系统的运动副和约束条件， 同时对各组成零部件赋予相应的材料属性， 如表1 所示。 主要涉及的运动约束关系包括： 曲轴与主／副轴承-旋转副； 曲柄销与滚针轴承-旋转副；十字滑环与动涡盘-移动副； 大平衡铁与曲轴-固定副； 小平衡铁与动涡盘-固定副； 皮带轮与曲轴-固定副。

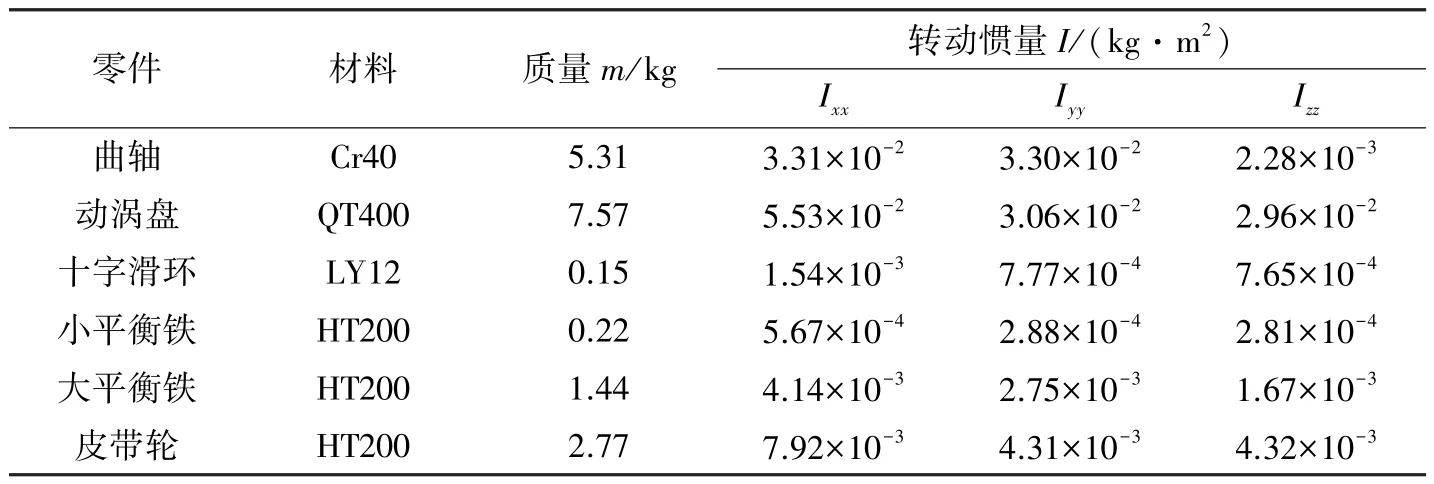
表1 材料构成及物理参数Table 1 Material composition and physical parameters

通过布尔运算将动涡盘与滚针轴承刚化为一体，利用Autoflex 模块对关键零部件（如曲轴、 动涡盘、十字滑环） 进行结构离散和柔性替换， 构建如图4 所示刚柔耦合模型。 图中显示了某阶激活模态下的曲轴振动模式， 可以很清楚地看到柔性曲轴的弯曲变形和应力分布。 在动力学仿真计算过程中， ADAMS／View会将柔性构件的应力和变形计入迭代过程， 以此来提高仿真结果的精度和可靠性。

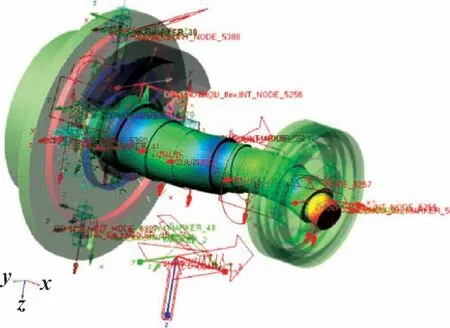
图4 主轴系统刚柔耦合模型Fig.4 Rigid flexible coupling model of spindle system

3.3 柔性接触仿真

在曲柄销与滚针轴承之间、 十字滑环与动涡盘之间设置柔性Contact 接触， 相关接触仿真参数见表2[15］。 ADAMS／View 采用基于Hertz 理论的Impact 函数处理接触问题， 由于Impact 函数同时考虑了构件的弹性力和阻尼力， 所以相当于利用非线性弹簧-阻尼模型来模拟实际中的接触碰撞。

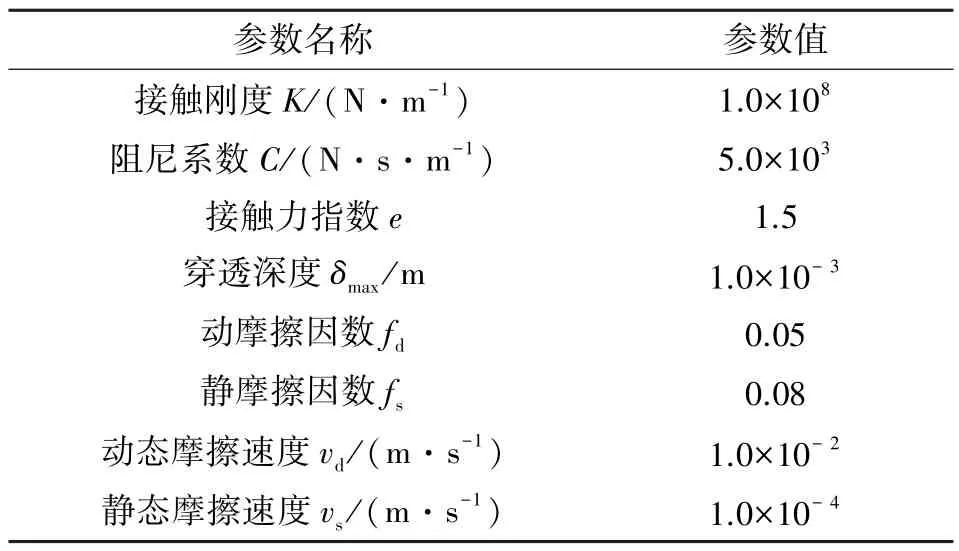
表2 接触仿真力学参数Table 2 Mechanical parameter of contact simulation

根据曲轴加工精度等级和曲柄销公差范围（0.01～0.05 mm）， 在曲柄销与滚针轴承之间设定4种间隙值， 即0 （理想状态）、 0.01、 0.03、 0.05 mm。 考虑到滑动副间隙影响， 在十字滑环与动涡盘键槽配合区域设定0.09 mm 间隙， 以此评估十字滑环在作平面运动过程中的接触碰撞。

对曲轴施加一个转速为2 400 r／min 的旋转驱动，设定仿真时间为0.1 s， 仿真步数为1 400。 在模型校验基础上运行仿真计算， 如图5 所示， 为某一间隙值下的主轴系统瞬时仿真形态， 不仅清晰地计算出了柔性构件的形变和应力分布， 而且还实时展示了曲轴、十字滑环与动涡盘之间的接触力（图中箭头所示） 变化， 有助于准确计算和分析柔性构件的接触碰撞机制。

图5 柔性体瞬时仿真形态Fig.5 Instantaneous simulation form of flexible body： （a） view 1； （b） view 2

4 结果分析与讨论

4.1 动涡盘加速度

动涡盘在YOZ面内绕主轴中心线作圆周轨迹平动， 不同运动副间隙下的动涡盘加速度变化曲线如图6 所示。 对比分析可知， 在理想状态下（间隙为0），动涡盘加速度曲线变化较为平缓， 但随着运动副间隙的增大，Y方向和Z方向的加速度曲线变化明显加剧， 且这种连续剧变在Z方向表现尤为突出， 说明动涡盘的Z向加速运动对于运动副间隙变化更为敏感。

图6 不同运动副间隙下动涡盘加速度Fig.6 Acceleration of scroll compressor at different joint clearance： （a） acceleration at Y direction； （b） acceleration at Z direction

从Y方向和Z方向的加速度曲线形态来看， 当间隙为0.01 mm 时， 加速度峰值及频率变化相对较大， 说明动涡盘的加速运动过程较为剧烈， 容易在气体压缩过程中产生振动或噪声； 当间隙为0.03 和0.05 mm 时， 加速度在Y方向和Z方向的曲线峰值及波动频率均有所减小， 相比之下， 更有利于动涡盘的平稳运动。 因此， 在非理想状态下， 0.03 和0.05 mm间隙值对动涡盘的加速运动影响相对较小。

4.2 十字滑环位移

动涡盘与静涡盘在形成封闭月牙形容积腔时， 必须借助十字滑环防止自转发生。 十字滑环主要在YOZ面内作平面运动， 其质心位移曲线如图7 所示。 比较分析可知， 在理想间隙下（间隙为0）， 质心位移在起始阶段由于柔性变形出现了小幅波动， 其余部分均为较为光滑的余弦曲线， 说明十字滑环位移连续平稳， 符合理想状态运行预期。 当间隙为0.01 mm 时，波峰区域的位移曲线相对理想状态发生了明显偏离，如图7 中放大图所示。 虽然偏离幅度很小， 但会在一定程度上造成十字滑环运动不到位， 进而引发动涡盘小幅自转， 影响容腔气体压缩效率及质量。 当间隙增大至0.03 和0.05 mm 时， 质心位移曲线与理想状态时基本一致， 整段未发生明显波动或偏离， 所以不会对十字滑环的平面运动产生较大影响。

图7 不同运动副间隙下十字滑环质心位移曲线Fig.7 Centroid displacement curves of cross slip ring at different joint clearance

4.3 曲轴质心轨迹

曲柄销与滚针轴承之间的运动副间隙有可能使曲轴出现径向跳动， 如图8 所示。 理想间隙下的柔性曲轴质心轨迹为一带有波动的非标准圆， 当间隙增大至0.01、 0.03 和0.05 mm 时， 曲轴质心轨迹与理想轨迹圆发生多处交叠， 说明曲柄销与滚针轴承之间存在多处接触碰撞。 此外， 各间隙轨迹圆之间也发生了相互交叠， 如图8 中放大图所示， 主要是因为柔性曲轴在高速状态下会产生不同程度的振动与变形， 致使不同间隙模型下的质心轨迹相互交叠。 可见， 柔性曲轴的质心轨迹对于运动副间隙变化尤为敏感。

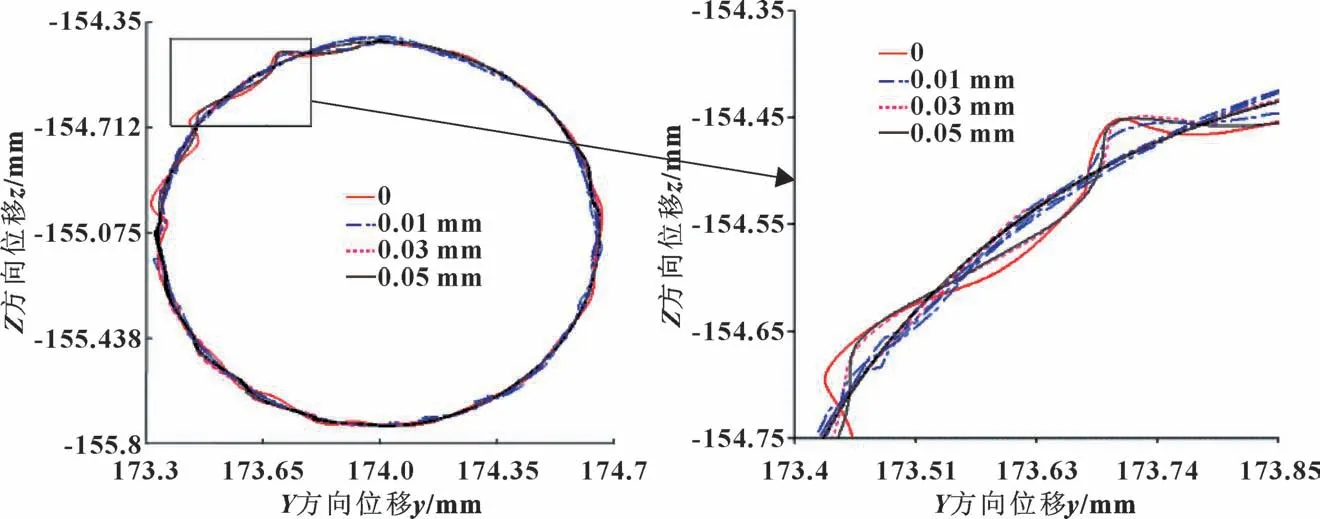
图8 不同运动副间隙下曲轴质心轨迹Fig.8 Centroid trajectory of crankshaft at different joint clearance

4.4 主、 副轴承支反力

由于偏心结构影响， 高速运转的主轴系统会对支撑轴承产生连续负荷[16］， 准确计算和掌握轴承系统的承载性能， 对于涡旋压缩机的高速化设计具有重要意义。 对比分析图9 与图10 可知， 在间隙为0时， 主、 副轴承支反力曲线波动幅度很小， 符合理想间隙轴承运行情况； 相比之下， 当轴承内部存在间隙时， 曲轴与轴承之间的碰撞力度和接触频率明显偏大。

进一步比较可知， 在Y方向上， 0.03 与0.05 mm间隙的曲线波动幅度及振荡频率明显大于0.01 mm，如图9 （a）、 图10 （a） 所示， 对比0.03 与0.05 mm间隙曲线发现， 前者多处曲线振荡峰值大于后者。 可见， 间隙对Y方向支反力的影响从大到小依次为0.03、 0.05、 0.01 mm。 与之不同的是， 随着间隙依次增大至0.01、 0.03 和0.05 mm，Z方向上的主、 副轴承支反力曲线振荡幅度反而在随之减小， 如图9 （b）、 图10 （b） 所示， 从曲线形态可以清晰看到，Z方向轴承支反力与运动副间隙大小成反比， 即间隙对Z方向支反力影响从大到小依次为0.01、0.03、 0.05 mm。

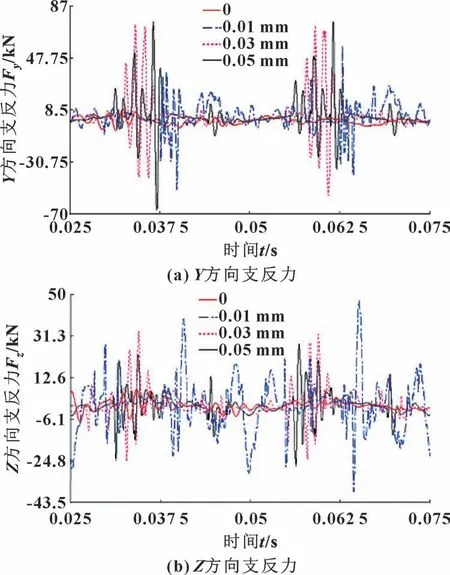
图10 不同运动副间隙下副轴承支反力Fig.10 Support reaction of auxiliary bearing at different joint clearance： （a） support reaction at Y direction； （b） support reaction at Z direction

总体来看， 在4 种运动副间隙状态下， 虽然主、副轴承支反力波动幅度不同， 但其在Y方向和Z方向上的曲线变化规律却十分相似， 即Y方向支反力幅值呈分段式大小交替变化， 而Z方向支反力峰值变化相对较小， 说明轴承在Z方向承受了更为连续和均匀的接触碰撞， 符合动涡盘Z向加速度分析预期。

4.5 间隙接触碰撞力

4.5.1 曲柄销与滚针轴承

非理想状态下的接触碰撞力会对封闭容积腔的形成和气体压缩产生不利影响， 如图11 所示， 在Y方向和Z方向上， 曲柄销与滚针轴承之间的接触碰撞力均沿正弦曲线呈周期性分布， 其中，Y方向的接触碰撞力均为正值， 说明只有曲柄销的一侧发生了接触碰撞， 而Z方向的接触碰撞力有正有负， 说明曲柄销的两侧均存在接触碰撞。

从图11 （a） 可以看出， 3 种间隙模型在Y方向上的碰撞力幅值较为接近， 但0.01 mm 间隙的碰撞频率基本都集中分布于波峰右侧区域， 容易造成轴承系统的应力集中和疲劳破坏； 相比之下， 0.03 和0.05 mm 间隙的力值频率相对分散， 且波峰左侧的力值和频域带宽明显大于右侧， 由此可知， 在一个曲轴回转周期（0～0.025 s） 内，Y方向碰撞区所承受的碰撞力及冲击频率沿正弦曲线从左至右逐渐减弱， 虽然碰撞过程为非对称不连续状态， 但不会形成应力集中。

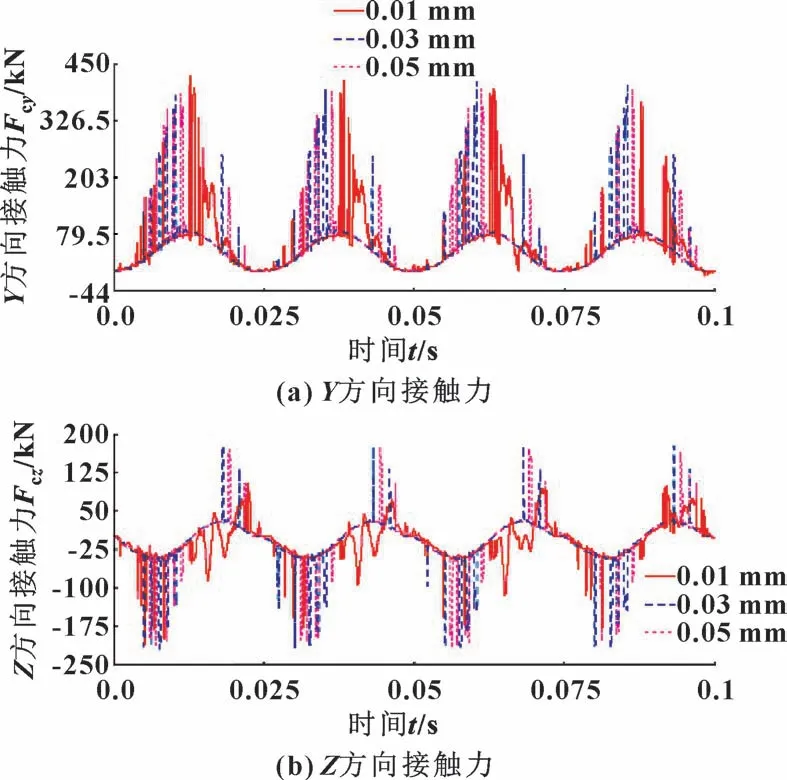
图11 曲柄销与滚针轴承接触碰撞力Fig.11 Contact force between crank pin and needle bearing at different joint clearance： （a） contact force at Y direction； （b） contact force at Z direction

如图11 （b） 所示， 在Z方向上， 0.01 mm 间隙的碰撞力幅值明显偏小， 而且冲击频率分布相对稀疏， 所以对Z方向的接触碰撞影响较小。 0.03 与0.05 mm 间隙的碰撞力分布区域基本一致， 且碰撞力幅值及频率无明显差别， 说明这两种运动副间隙在Z方向产生的接触碰撞效果相似。

4.5.2 十字滑环与动涡盘

在涡旋压缩机运行过程中， 由于运动副间隙的存在， 十字滑环会与动涡盘在键槽配合区域产生接触碰撞[17］， 如图12 所示， 可以很清楚地看出， 当间隙为0.01 mm 时，Y方向和Z方向上的接触碰撞力波动幅度明显大于间隙为0.03 和0.05 mm 时， 说明十字滑环在极限位置附近受到了较大冲击， 使其容易偏离理想轨迹， 符合十字滑环质心位移曲线分析预期。

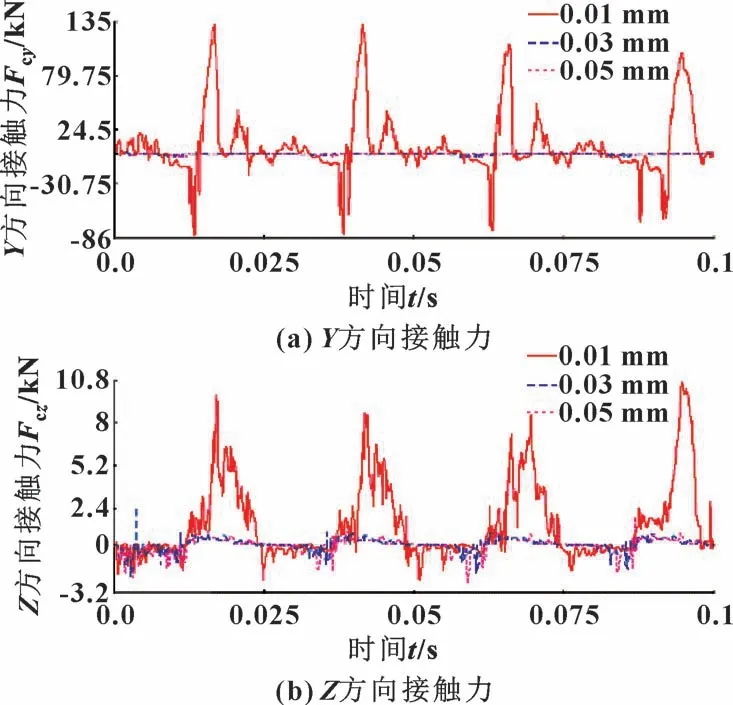
图12 十字滑环与动涡盘接触碰撞力Fig.12 Contact force between cross slip ring and scroll compressor at different joint clearance： （a） contact force at Y direction； （b） contact force at Z direction

相比之下， 由0.03 和0.05 mm 间隙产生的接触碰撞力， 虽然在Y方向上基本趋近于0， 但在Z方向上却具有相近的幅值及频率， 且接触力曲线未发生较大突变和波动， 说明十字滑环运动相对平稳。 因此，考虑到十字滑环的防自转作用， 应优先选择0.03 mm或0.05 mm 运动副间隙。

5 结论

（1） 不同运动副间隙下动涡盘的加速运动以Z方向为主。 当运动副间隙为0.01 mm 时， 动涡盘加速度变化较为剧烈， 容易引发系统振动或噪声； 当间隙增大至0.03 和0.05 mm 时， 加速度变化对动涡盘运动影响相对较小， 有利于封闭容积腔的形成和气体的稳定压缩。

（2） 在理想间隙（间隙为0） 下， 柔性曲轴质心轨迹为一带有波动的非标准圆。 当运动副间隙增大时， 由于柔性曲轴存在一定的振动和变形， 使其质心轨迹圆与理想轨迹圆发生多处交叠， 说明在非理想间隙状态下， 曲柄销与滚针轴承之间存在多处不可避免的接触碰撞。

（3） 与Y方向相比，Z方向上的轴承支反力波动幅度及频率相对平稳， 说明主、 副轴承在Z方向上承受了更为连续和集中的接触碰撞。

（4） 为避免轴承系统发生应力集中和疲劳破坏，同时考虑到十字滑环的防自转作用， 在配置曲柄销与滚针轴承运动副间隙时， 应优先选择对接触碰撞载荷及频率影响较小的0.03 mm 或0.05 mm 间隙。