异质信息网络中基于元结构的影响力最大化

徐智敏，周丽华

(云南大学信息学院，云南昆明650504)

1 引言

社交网络的发展为信息的全球传播和新闻的有效传播带来了新的潜力，人们可以直接参与这些社交网络，建立自己的友谊网络，并相互分享他们的观点、见解和经验。而确定网络中有影响力的成员被视为这种潜力付诸行动的关键因素，影响力最大化问题由此被提出。

Domingos等人[1]首先将影响力最大化问题建模为一个算法问题。Kempe等人[2]首次将影响力最大化问题定义为一个离散最优问题，并证明该问题是一个NP-hard问题，同时提出了贪心算法得到了该问题的一个近似解。但贪心算法的时间复杂度过高，无法高效解决大规模网络问题。对此研究者们相继提出了许多启发式算法[3，4]或改进贪心算法[5，6]以提高运行效率。然而这些方法仅针对同质信息网络进行考虑，即只考虑了一种对象类型和一种关系类型，忽略了对象之间的异质关系和潜在的语义信息。

异质信息网络[7]是一种包含了多种对象类型和多种关系类型的信息网络，能够更加合理的描述真实的社会网络。因此，在异质信息网络上进行影响力最大化研究更具有现实意义。近些年来，影响力最大化研究的焦点逐渐转向异质信息网络。杨等人[8]通过多种元路径提取不同对象之间关系，来度量节点的影响力。Kuhnle等人[9]提出了多重网络上的影响力最大化算法等。但由于异质信息网络具有复杂的网络结构，如何高效的利用异质信息一直是异质信息网络分析的难点问题。

本文的目的是在异质信息网络中研究相同类型对象的影响力最大化问题，并提出了基于元结构的影响力最大化算法(MSIM)。异质信息网络中包含了丰富的语义信息，元路径可以有效地捕获源对象和目标对象间的单一关系，但无法捕获到它们之间的复杂关系。而元结构本质上可以看作多条元路径的集合，能够方便的表达对象间复杂的关系。因此，在MSIM算法中采用元结构存储目标对象与网络中所有类型对象间的语义关系，并且引入信息熵来度量节点的影响力，提出了路径熵度量不同元路径对源节点的影响贡献，然后整合了元结构中不同元路径的路径熵提出了结构熵度量源节点的最终影响。最后在真实数据集上进行实验，验证了该算法的有效性。本文的贡献主要包含以下三个方面：

1) 提出了一种基于元结构的信息熵影响力最大化算法(MSIM)，该算法为每个目标类型节点构造一个元结构，存储不同对象之间的异质关系；

2) 提出了路径熵(PE)和结构熵(SE)来评估一个节点在异质信息网络中的重要性，PE值反映了单条路径对源节点的影响，SE值反映了局部结构对节点的影响；

3) 在两个真实数据集上验证了MSIM算法的有效性和效率，并证明MSIM算法在效率和性能上有较好的折中。

2 相关工作

影响力最大化问题在2003年首次被定义为一个算法问题，Kempe等人[2]证明了该问题是一个NP-hard问题，并提出了贪心算法，该算法具有高精度的近似结果，但也有着高昂的时间代价，难以拓展到大规模网络问题的应用。为了克服传统的贪心算法的低效性，研究者们对传统的贪心算法进行了一系列的改进，或者提出了新的启发式算法。刘等人[10]基于局部节点优化和折扣度构造了节点近似影响值函数来计算局部节点的影响值。曹等人[11]提出了基于核数层次特征和影响半径的启发式算法。聂等人[12]将信息熵引入复杂网络以计算节点的影响力，使用信息熵度量不同邻居对节点的影响。然而这些方法均为同质信息网络的研究方法，未考虑到不同类型对象之间的连接关系。

随着社交媒体的快速发展，异质信息网络已被提议作为真实世界图或网络的一般表示。目前关于异质信息网络的研究主要集中在聚类、分类、相似性搜索链路预测等，而关于异质信息网络的影响力最大化研究相对较少。李等人[13]通过限制相同类型节点间的最短路径从异质信息网络中抽取一个同质子图，并根据节点对在异质信息网络中的路径来确定子图中节点间的影响。杨等人[8]利用元路径在异质信息网络中提取出多个同质子图进行影响力最大化研究，但使用独立的元路径进行对象之间关系的提取，会忽略一些对象被多条边共享的问题，会导致这些信息的损失。

3 相关概念

本节主要介绍异质信息网络和信息熵中的基本概念，这些概念是本文工作的基础。

定义1 异质信息网络[7]：异质信息网络是具有一个对象类型函数α和一个关系类型函数β的有向图G=(V，E，T，R)。其中V是节点集，E是边集，T是节点类型集合，|T|>1，R是关系类型集合，|R|>1，α：V→T是节点和节点类型的映射，β：E→R是边和关系类型的映射。如图1描述了异质信息网网络DBLP的一个网络实例，它描述了不同类型实体之间的关系，如Bob和Ada曾合作发表了论文P2。

定义2 异质信息网络模式[14]：异质信息网络模式记为TG=(T，R)，是带有对象映射函数α：V→T和关系映射函数β：E→R的异质信息网络G=(V，E，T，R)的元模板。

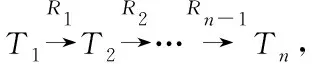
定义4 元结构[16]：元结构可以看作由多条具有公共节点组成的有向无环图，形式化地，元结构可以记为M=(VM，EM)，其中VM是节点集合，EM是边集合。

定义5 信息熵[4]：信息熵是一个系统的信息含量的量化指标，常用来作为系统方程优化的目标或参数选择的判据。乔等人[4]将信息熵引入复杂网络以计算节点的影响力。对于网络中的任意节点v的信息熵可以由式(1)计算

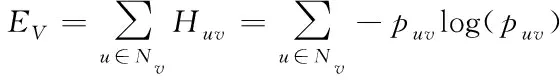
(1)

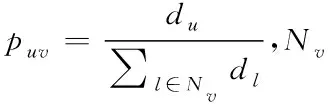
4 基于元结构的影响力最大化建模

在这一部分，本文提出了一个基于元结构的影响力最大化算法模型(MSIM)，采用的数学符号及含义见表1。

表1 符号说明

4.1 问题定义

本文选择以异质信息网络中的信息传播为例，研究异质信息网络的影响力最大化问题。给定一个异质信息网络G=(V，E，T，R)，本文的目的是在考虑在度量节点的影响力时利用异质信息网络中丰富的语义信息，考虑不同类型节点之间的影响，在特定的扩散模型下，选择出具有最大影响范围的相同节点类型的子集。

4.2 构造元结构

为了度量节点的影响力，本文为每一个目标类型节点u∈V构造一个元结构MSu，并且将u作为元结构中的源节点，根据网络模式不同类型节点之间的关系，查找出节点u的出邻居加入MSu，然后根据网络模式中u的出邻居所属的节点类型与其它节点类型节点的关系，将出邻居的出邻居添加至MSu，直至遍历网络模式中u与所有类型节点之间的关系。在构造元结构的过程中保留节点本身的度的信息。如图2描述了图1中作者Ying的元结构的构造过程。本文通过网络模式提取出目标节点的元结构能够有效的保留局部结构信息和节点间的异质信息，而本文对节点影响力的度量也将以节点的元结构为基础。

图2 元结构构造示例

4.3 路径熵与结构熵

元路径可以提取源节点与目标节点的关系，对于以v1为源节点的元路径W，路径w(v1v2…vn)是W的一条路径实例，本文由式(2)计算元路径W对源节点v1的路径熵。

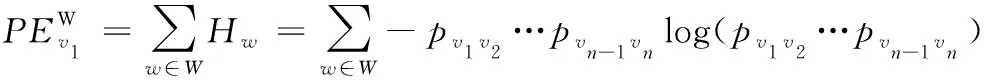
(2)

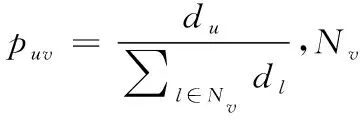
社交网络中的三度影响力理论指出信息在网络传播过程中存在衰减，并发现三度之内的节点属强连接关系，而距离三度之外的节点间为弱连接关系，信息在弱连接中基本不产生影响。因此，本文对多介质元路径进行“折半”处理，只计算其前驱的路径熵，如对于元路径APTPA，只计算元路径APT对源节点所提供的路径熵。在本文构造的所求影响力最大化的目标类型节点的元结构中能够有效的存储多介质元路径的前驱信息，以及目标节点与其它类型节点间的联系。对于节点v1的元结构MSv1，综合由不同元路径W的路径熵得出v1的结构熵，由式(3)计算节点的结构熵。

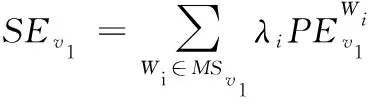
(3)

其中λi为元路径Wi的影响因子。

4.4 MSIM算法描述

本文提出了在异质信息网络中基于元结构的影响力最大化算法(MSIM)。MSIM算法构造节点的元结构，并定义节点的结构熵度量源节点的影响力，也考虑了不同类型的元路径对节点影响力的影响。元结构的构建有利于根据不同的扩散任务，有针对性的选择种子节点。如在DBLP网络中选择作者节点作为影响力最大化的研究目标，那么MSIM通过构造作者节点的元结构来度量作者的影响力。通过元结构中不同的元路径的结合来度量节点的影响，既考虑到了节点的局部影响也考虑到了节点的全局影响。MSIM算法伪代码如下所示。

MSIM算法伪代码

1)输入：G(V，E，T，R)，种子集节点数量k

2) 输出：种子集合S

3)初始化S=φ

4)Foreachu∈V，

5)构造元结构MSu

6)由式(2)(3)计算节点的结构熵MEu

7)Endfor

8)Fori=1tokdo：

9)s=max(MEu)

10)S=S∪{s}

11)Endfor

12)ReturnS

5 仿真验证

5.1 数据集准备

本文在真实的异质信息网络数据集DBLP数据集和YELP数据集验证MSIM算法的性能。数据集的详细描述如表2所示。为了验证所提出的MSIM算法的有效性，本文采用同质信息网络中基于信息熵的影响力最大化算法ME算法[12]，以及异质信息网络中基于同质子图的Entropy算法[13]和MPIE算法[8]作为对比算法。

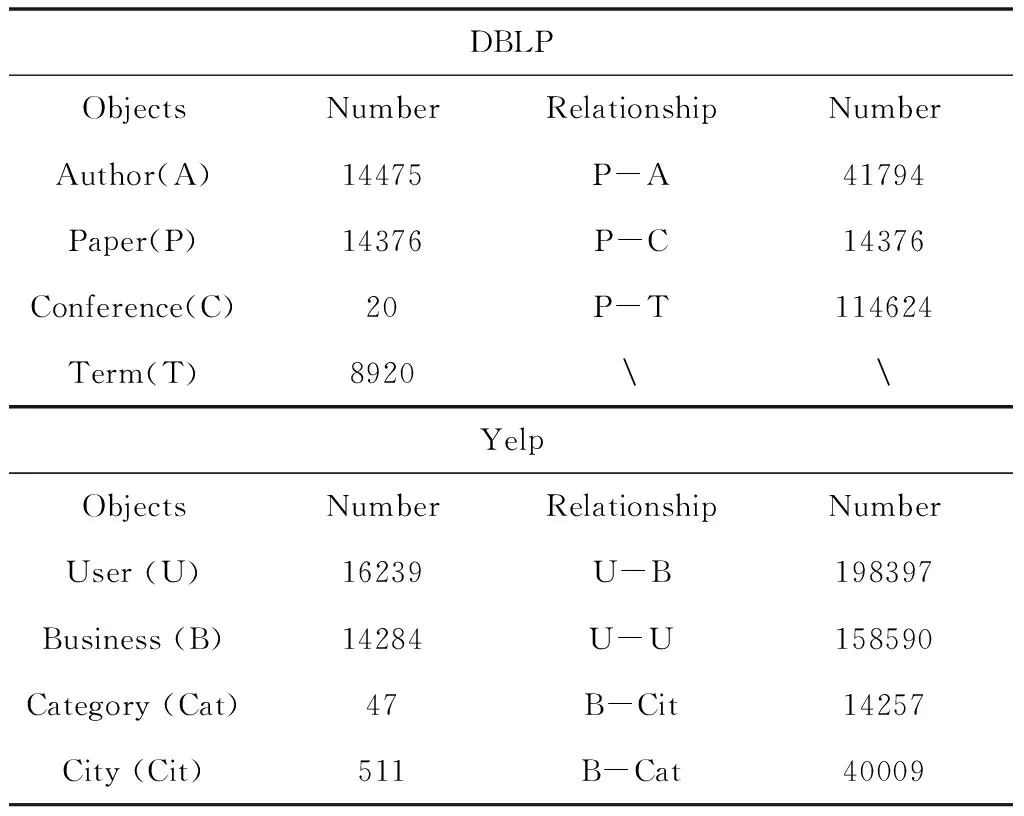
表2 数据集详细信息

5.2 有效性验证

为了验证MSIM算法的性能，本文在DBLP和YELP数据集上进行实验。对于同质信息网络中的ME算法，实验中不区分节点类型与边类型。分别选取k个DBLP网络中的作者节点和YELP网络中的用户节点作为种子节点，k分别选取10，20，30，40，50个节点。通过LT模型进行扩散模拟，采用影响范围(InfluenceSpread)作为评价指标，影响范围定义为成功激活节点的数量。图3展示了不同算法对不同k个影响节点的影响扩散范围，其中横坐标表示种子集合大小，纵坐标表示最终激活节点数量。

从图3中可以看出，不同算法在不同的数据集上表现出不同的性能，并随着k值的增加，最终激活节点的数量也会增加。在这些算法中，所提出的MSIM算法优于同质信息网络的ME算法，表明考虑节点的异质信息可以提高扩散影响范围。MPIE算法、Entropy算法在不同的数据集表现出不同性能，其中MPIE算法在DBLP数据集中的表现较差，而在YELP数据集中性能有所提升，这说明在异质信息网络中提取同质子图进行影响力最大化研究依赖数据集的结构特征。而本文依据异质信息网络的网络模式为节点构造的元结构，并且基于元结构提出的MSIM算法在两个数据集上都有较好的表现。因此，本文所提出的元结构是有意义的，它能够较好的保留节点的结构信息和不同类型节点间的异质关系，有利于影响的扩散，使传播更加广泛。

图3 不同算法的扩散结果

5.3 效率对比

本文在DBLP数据集中对比了不同算法之间的时间效率，将种子节点的数量k大小分别设为10，20，30，40，50，对比不同算法选择出k个种子节点的运行时间，在表3中展示了在DBLP和YELP数据集上的运行结果。从表3中可以看出所有算法的运行时间随着k值的增大而增加，但增加幅度较小。ME算法不需要考虑数据集中节点和边的异质性，有着较低的时间复杂度。Entropy算法的运行时间主要消耗在构建同质子图以及确定子图中节点的传播影响概率。MPIE算法需要根据不同的元路径构建多个同质子图，且根据不同元路径构造子图的运行时间不同，总体时间复杂度过高，未加入对比。MSIM算法的运行时间主要花销在构建节点的元结构，较于构造同质子图，有较低的时间复杂度。综合来看MSIM算法在时间效率和性能上有着较好的折中。

表3 运行时间

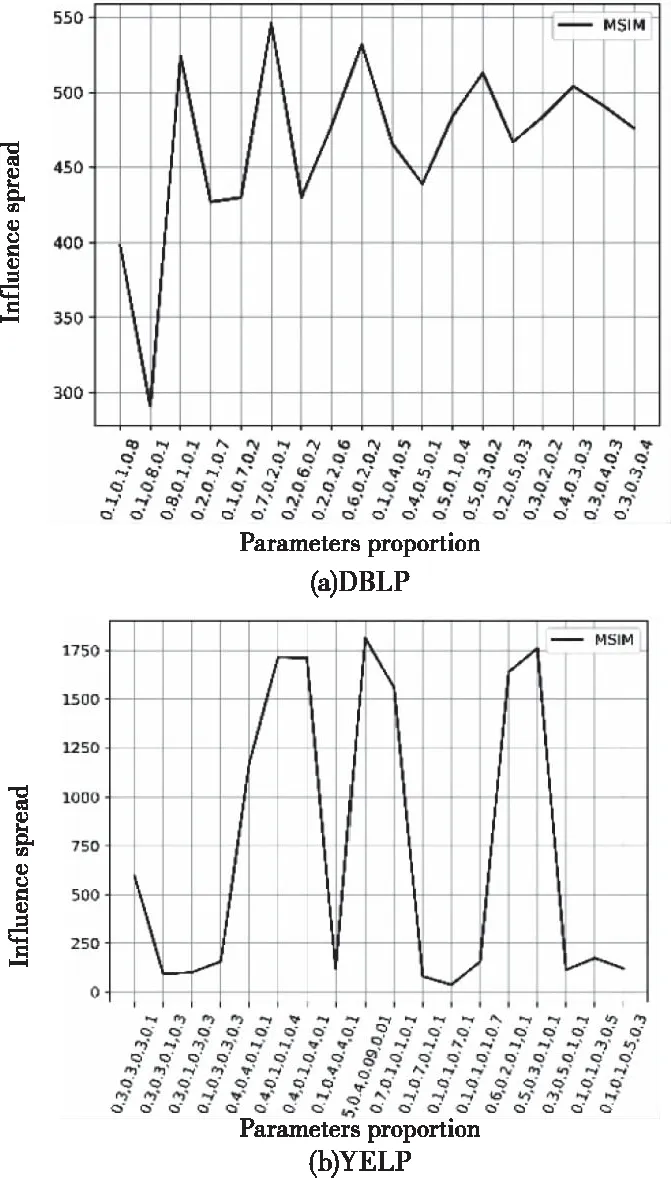
图4 参数分析

5.4 参数影响分析

本文设置元结构中不同的元路径的影响因子的和为1，在DBLP数据集和YELP数据集中选取了18组参数，选出k=50个种子节点并比较它们的影响范围，实验结果如图4所示，其中DBLP横坐标表示元路径APA，APCPA，APTPA的影响因子，YELP横坐标表示元路径UU，UBU，UBCatBU，UBCitBU的影响因子。从图4中可以看出不同的影响因子比值会有不同的扩散结果。在DBLP网络中当影响范围达到最大值时，元路径APA的影响因子是三种元路径中的最大值，这表明具有公共论文作品的作者的关系在扩散过程中起着关键作用，在进行有效性验证实验采用AP，APCPA，APTPA的影响因子为0.7，0.2，0.1。在YELP网络中当影响范围达到最大值时，元路径UU具有最大的影响因子，这表明用户之间的交互在扩散过程中起着关键作用，在进行有效性验证实验时采用UU，UBU，UBCaBU，UBCiBU的影响因子为0.5，0.4，0.09，0.01。

6 总结与展望

本文研究了异质信息网络中的影响力最大化问题，旨在利用异质信息网络中丰富的语义信息度量节点的影响。在此基础上，提出了一种基于元结构的信息熵模型来度量异质信息网络中节点的影响力，即MSIM。该算法通过为节点构造元结构来捕获异质信息网络中的丰富的语义信息，并通过路径熵与结构熵度量节点的影响。然后在真实世界数据集上进行实验，证明了所提方法的有效性。但在本文中，只考虑了相同类型对像的影响力最大化，因此在未来研究中，可以考虑包含有不同类型对象的节点集的影响力最大化，这有助于在实际系统中提供更准确影响度量。