一种水下无线传感器网络的密钥提取方法
2023-03-29徐晨,王彪
徐 晨,王 彪
(江苏科技大学,江苏 镇江 212003)
1 引言
随着人类对海洋的探索开发,水下通信逐渐引起了人们的广泛关注。水下无线传感器网络(Underwater Wireless Sensor network,UWSN)凭借极大的通信的自由度被广泛的应用于环境检测、资源开采、军事等领域[1]。但是,由于水下声信道的开放性和声传输的广播特性,UWSN很容易遭受敌手的侦听[2]。传统的UWSN安全机制主要依靠以数学难题为基础的对称加密和非对称加密体制,试图通过计算的复杂程度来防止需要传输的密文信息被窃取[3-5]。这种安全手段毫无疑问会带来较高的能耗,而且,随着传感器节点个数的增加,需要的密钥数量呈指数级上升,密钥的分发、存储和管理等过程也会带来巨大的开销。然而,UWSN是由电池供电,节点的内存、计算能力十分有限,并且密钥管理设施一旦被攻破,那么其所服务的节点将不再安全。利用水声信道固有的随机传播特性完成密钥分发的物理层安全方案不需要进行数学难题的运算,避免了不必要的开销,是一种轻量级的方案。因此,该物理层安全方案逐渐引起了学者们的重视。文献[6]将物理层安全方案引入水下通信系统,首次提出了具有鲁棒性的基于水下信道特征的密钥生成方案。文献[7]将信息隐藏技术和文献[6]中的密钥生成技术相结合,确保水声信息的隐蔽传输,为水声隐蔽通信提供了加密支持。文献[8]利用接收信号强度RSS以及OFDM系统来生成密钥。然而RSS是一种粗粒度的信道测量值,不能完全使用信道信息,且变化缓慢,容易造成长连1或长连0。文献[9]中提到一种基于量化保护带的信道量化(CQG)算法。这种算法高效的量化出信道特征值,然而大量保护带的设立造成了信道资源的浪费。文献[10]中提出了另一种信道量化方案,利用相位的均匀特性实现MAQ算法。然而相位容易受到噪声、频偏的影响,实际情况下很难维持相位的稳定性,量化出的密钥很大概率不能使用。上述文献都是基于水下信道特征实现对数据的加密,本文主要是在文献[9]的基础上,对文献[9]中的算法进行改进。改进的CQG算法减少了信道特征的不必要浪费,并且在密钥不一致率几乎不变的条件下,大大提高了密钥的生成效率。
2 物理层安全原理及模型
2.1 物理层安全原理
水下无线信道是一个复杂的随机信道,声源发出的信号由不同声线向水中扩散,经过反射和折射最终到达接收端,产生丰富的多途效应,其表达式如下
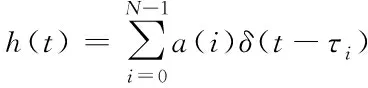
(1)
其中,N代表多途路径数,a(i)代表第i条信道的传输衰减,δ(t-τi)代表第i条信道的传输时延。同时,无线信道具有短时互易性,系统工作在时分双工(Time Division Dual,TDD)模式的一个相干时间Tc内,信道几乎不产生变化。即在相干时间Tc内hab=hba;而超过一个相干时间Tc,无线信道呈现出时变性,由于多途效应的存在,信道将会发生剧烈的变化,即hab≠hba。信道的这种随机变化为无线密钥的生成提供了天然的随机源;信道还具有空变性,两个节点之间的距离如果超过λ/2,其中λ代表声波的波长。则从同一主节点发送来的信道探测序列表现出不同的信道特征。
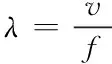
(2)
v代表声波速度,f代表通信频率。声波在水中传播的速度约为1500m/s,中距离水声通信频段为10kHz数量级,意味着只要窃听节点在合法节点0.015~0.15m以外的位置,就无法提取与合法节点相同的信道特征。因而,通信双方间的信道被非法节点窃听的概率非常低。无线信道固有的特性充分的保证了物理层通信的安全。倘若非法节点想要有效地窃取该信道信息,就必须非常靠近合法通信节点的任意一方,这时非法节点暴露的风险也非常高。
2.2 物理层安全模型
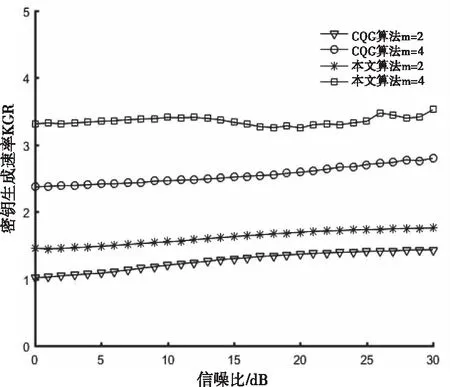
考虑一般UWSN物理层安全模型如图1所示。该模型由合法传感器节点Alice和Bob,窃听器节点Eve以及水声多途信道构成,系统的工作模式为TDD模式。为了侧重分析密钥生成环节,假定Alice和Bob之间的信道探测满足信道互易性即T1+T2< 下面对物理层安全模型进行分析,不失一般性地,设Alice为主节点Bob为从节点,主节点Alice在T1时隙向Bob发送信道探测序列sa(t),Yab(t)为从节点Bob接收到的探测信号,Yae(t)为窃听节点Eve接收到的信号。 Yab(t)=hab(t)*sa(t)+nab(t) (3) Yae(t)=hab(t)*sa(t)+nab(t) (4) Yba(t)=hba(t)*sb(t)+nba(t) (5) Ybe(t)=hbe(t)*sb(t)+nbe(t) (6) 根据第2节所述的物理层安全原理及模型,提出一种改进的CQG算法。其步骤可总结如下: 1) 合法通信双方互发探测序列进行信道特征提取; 2) 对估计信号进行预处理; 3) 对预处理后的信号提取GIB序列并进行量化; 4) 保留GIB=0的量化值,提取GIB=1的CIR进行二次平滑量化。 根据2.2节所述,接收端接收到的信号可以概括为以下表达式 y(t)=h(t)*s(t)+n(t) (7) Alice根据接收的信号估计信道特征值CIR: hab(t)*sab(t)=yab(t)-nab(t) (8) hab(t)=yab(t)/sab(t)-nab(t)/sab(t) (9) (10) 同理,Bob根据接收的信号估计信道特征值 CIR: (11) 由式(11)可知,估计信号包含信道增益和经过处理的加性干扰,因此必须对估计信号的噪声进行去除处理,考虑到水下节点的能耗与计算存储能力,采用简单可靠的滑动平均(SMA)算法进行去噪处理。SMA算法是对时间序列前N个点的通用平滑方式。每一个点在时间序列中占有相同的权重值。 (12) 其中,hk表示估计序列的第K个值,N表示滑动平均滤波窗口的大小,将 SMA 的值作为估计CIR序列去除噪声后的值。 经过预处理后的CIR可以作为随机源进行量化处理。CIR是一种非均匀分布,采用等间隔均匀划分会降低密钥熵。因此采用等概率量化使密钥熵值最大,即每一块量化区间等概率出现。从信息论的角度,密钥熵可以表示为 (13) 密钥熵值在等概率时达到最大,密钥熵越大,单符号的不确定性越高。等概率划分时 (14) H(X1)=log2 (15) 等间隔划分时P(X1=0)≠P(X1=1),显然H(X2) 多比特量化带来的问题是:量化边界处的信道特征值对波动异常敏感,细微的差错就容易使合法双方的信道特征值量化到不同的区间。加性噪声是引起这一现象的主要原因,尽管预处理平滑了大部分随机噪声,但是不能使得合法双方处理后的信号完全一致,这就导致了判决错误。单个信号特征值量化的比特位数越多,量化的区间也随之增大,通信双方对信道测量的精确程度就有更高的要求,信道估计差异造成了较高的密钥不一致率(Key Disagreement Rate,KDR),这会严重影响密钥生成算法的性能。因此在量化区间边界处增设量化保护带并引入保护带指示位(GIB),用l=(l1,l2,…li),i=2m+1表示没有加入量化保护带的量化区间。保护带比例为可调参数r(0 (16) Alice和Bob通过比较CIR序列与量化保护带,分别得到一组GIB序列,当CIR值在区间[g(j),g(j+1)],i mod 2=1之间时,GIB=0;当CIR值在区间[g(j),g(j+1)],i mod 2=0之间时,GIB=1。并通过信道进行传输,假设GIB序列的交互是无差错进行的。当合法节点接收到对方的GIB值时,经典的做法如表1。 表1 GIB序列对 CIR的影响 通过表1可知,当节点观察到特征值落入保护带内GIB=1,意味着这个特征值可能会发生不匹配,因此节点不应该使用该信道特征值来量化密钥,该特征值将被丢弃。只有GIB序列同时为0的CIR得到保留。即同时落在保护隔离带外的CIR才能最终根据格雷码(Gray code)进行编码。值得注意的是GIB序列没有向窃听者提供任何关于密钥符号的信息,因此不会影响保密性能。通过适当调整保护带的大小,可以减小节点在量化区域边缘附近出错的可能性。实际上,信噪比在不是特别恶劣的情况下,经过平滑处理的特征值表现出良好的相关性,大范围的测量值偏移很难发生。如图2所示,是一个CIR值量化成两位密钥比特的例子,需要4个等概率量化区间。等概率量化区间在图2中用实线表示,并对等概率区间加入量化隔离带,在图2中用虚线表示。任意取出经过平滑处理的Alice和Bob的100个CIR测量值做对比。可见,如果没有量化保护带,由于编码采用格雷码且没有CIR值发生突变。直接量化落入量化保护带的值,大概率会量化成完全一致的密钥比特,或者密钥比特只含有一位错误。这虽然使得KDR大大降低。但是这样的做法造成了大量的信道特征序列浪费,密钥生成速率(Key Generation Rate,KGR)随之降低。 为了提高CQG算法的KGR,考虑合法通信双方在生成初始密钥并发送GIB序列后,都为0的密钥保留;只要有一方GIB序列为1,仍然删除对应的密钥。同时记录下只要有一方GIB序列为1的对应信道特征值,这些信道特征值构成新的向量LA和LB,LA和LB各自在本地进行二次平滑滤波,同时落入量化隔离带的信道特征值具有较强的相关性保证了二次平滑依然会有良好的滤波效果。对二次平滑后的LA,LB重新划分等概率区间并增设量化保护带,按照表1的方式进行处理,将新得到的密钥比特置于初始密钥比特后方。量化后生成的密钥比特仅是未加工的密钥,还需要进行密钥协商和隐私放大2个步骤来获取最终密钥。由于本文的重点在于探究量化算法,对于密钥协商与隐私放大仅采用简单的Cascade协议[11]以及散列函数分块确认机制。 图2 合法节点CIR值的对比 本文采用Matlab R2016b进行仿真。Alice和Bob互相发送探测序列,探测序列经过多途信道后到达接收端。根据接收到的信号提取CIR值后,首先对CIR进行平滑滤波去噪处理,再对去噪后的CIR进行改进的CQG算法得到最终密钥。仿真参数由表2给出。本次仿真分别从密钥生成速率KGR、密钥不一致率KDR、密钥随机性这三个方面将本文改进算法与CQG算法进行对比分析。 表2 仿真参数 在CQG量化算法中,量化保护带r影响着KGR与KDR,当r升高时,有利于保证生成密钥的一致性;当r降低时,密钥速度有所提升,但是一致度不够,本次仿真选取量化保护带r为0.2,选取量化比特数m=2和m=4分别比较本文算法与CQG算法的KGR与KDR情况。KGR如图3所示,KDR如图4所示。 图3 信噪比与密钥生成速率的关系 图4 信噪比与密钥不一致率的关系 从图3中可以看到,随着信噪比的提高,所有量化算法的KGR均呈现上升态势。这是因为外界加性干扰减弱,对量化算法的影响逐渐减小,Alice和Bob的CIR值相关性提高。然而相关性提高,不应该被删除的密钥比特数仍然被删除,浪费的密钥比特率反而提高。理论上来说这种重新平滑机制可以通过无限制重传来提高KGR。然而这会造成额外的通信开销,两个算法中合法节点都需要互发一次GIB序列,本文算法通过接收到的GIB序列进行二次平滑避免删除造成的浪费,在没有额外付出通信开销的情况下,实现了KGR的大幅提升。例如,在信噪比都取15dB的情况下,本文算法比CQG算法的生成效率提高了32.44%。由图4可以看到,随着信噪比的提高,所有量化算法的KDR均呈现下降态势。这是因为Alice和Bob的CIR值相关性增大,且CQG算法只量化双方同时在量化保护带外的特征值,因此KDR足够的低,可以明显看到本文算法与CQG算法相比,KDR基本保持不变,甚至在低信噪比时,优于CQG算法。在KDR基本不变甚至略微优于CQG算法的前提下,KGR大幅提升是本文算法的优势所在。 除了密钥生成速率KGR和密钥不一致率KDR,密钥随机性也是衡量密钥质量的标准,本文通过美国国家标准与技术研究所(NIST,NationalInstituteofStandardsandTechnology)随机性测验中的九项测试[12],说明本方案生成的密钥的随机性。输入密钥串进测试指标都会输出一个P-value值,P-value>0.01即为通过测试,密钥随机性越好代表生成的密钥安全系数越高,越不容易被敌手破解。测试结果如表3所示。 表3 NIST随机性测试结果 针对水下无线传感器网络计算能力有限的问题,本文提出了一种轻量级的物理层加密算法来规避复杂的计算。该算法通过平滑处理的方式保留了大部分相关性高的信道特征值,并将信道特征值作为量化源进行量化。将GIB序列中本该删除的信道特征值提取出来,进行二次平滑量化。通过仿真,证实了该算法在密钥不一致率基本不变的情况下,可以大幅提升密钥生成速率。但是,在低信噪比时,密钥不一致率仍然在一个较高的水平,下一步将继续研究密钥协商算法来进一步降低密钥不一致率。
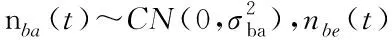
3 基于改进CQG的密钥生成方案
3.1 信道特征提取
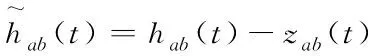
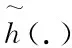
3.2 预处理

3.3 改进的CQG算法

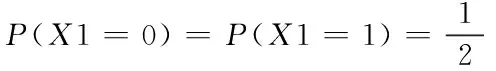
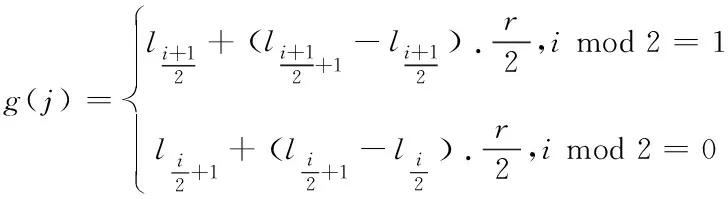


4 仿真结果分析



5 结束语
