基于分离卷积二值化网络的模型压缩方法研究

张 雷，杨薪颖

(沈阳航空航天大学电子信息工程学院，辽宁 沈阳 110136)

1 引言

目前，深度卷积神经网络(DeepConvolutional Neural Network，DCNN)已经广泛应用于图像分类[1]、人脸识别[2]、音频分类[3]和语音识别[4]等研究。在DCNN快速发展的同时，网络的层数和模型的体积也在不断扩大，规模的扩大和计算复杂度的增加使得这些模型很难部署[5]和应用于实时性要求较高的场景，阻碍了其在更广阔领域的应用和推广，因此，优化卷积神经网络结构，压缩并加速网络模型已成为工业界和学术界亟待解决的难题之一。为了解决这一问题，大量的网络模型压缩方法被相继提出[6-11]。

目前具有代表性的网络模型压缩方法有五种：权重剪枝法、近端梯度法、知识蒸馏、深度可分离卷积和二值化。权重剪枝法[6]在早期的神经网络时期就已经被提出，其主要通过减少网络全连接层中的权重数量，从而达到减少网络中的冗余、提高网络计算效率的要求，在不显著影响精度的情况下删除一部分网络权重，最终可以减少数十倍的内存需求。相对于传统的随机梯度下降法，近端梯度法[7]则是在目标函数中加入L2范数正则化项，产生稀疏模型，这种方法不仅可以避免过拟合问题，而且提高了网络收敛速度，缩短了训练时间。不同于以上两种方法，知识蒸馏[8]法通过构建出新的小网络来达到压缩模型的效果，将一个高精度且复杂的教师网络转换为一个结构紧凑简单的学生网络，教师网络将细粒度知识迁移到学生网络中，进而使学生网络和教师网络拥有同样的性能。深度可分离卷积[9]与权重剪枝类似，通过减少了参数数量来优化网络模型，其已经广泛应用于一些轻量级网络中，如Google所提出的Inception[12]、MobileNet[13]和SqueezeNet，该方法的核心思想是将一个完整的卷积运算分为两步，相比与标准的卷积操作，不仅可以有效的提取特征，还极大的减少了参数量，降低了运算复杂度，通过深度可分离卷积，在CPU上可以实现2到4倍的加速，并且可以保持分类精度。二值化网络[10]又称为二进制神经网络，主要思想是将网络参数值量化为+1或-1，使原本32位的浮点数参数量化至1位定点数，此外，其纯逻辑计算极大得压缩了网络模型，并保持了与原始模型中相同的参数数量，在分类MNIST数据集时，速度可提升7倍[14]。上述方法均已在模型压缩与优化加速技术中成功地应用与普及。

本文结合深度可分离卷积和二值化网络两种模型压缩方法，设计了一种深度可分离卷积二值化网络模型，使用深度可分离卷积代替标准卷积，再对网络进行二值化，并通过实值教师网络引导训练使二值化网络模型在最大化压缩的同时保持了分类精度。实验结果表明，深度可分离卷积二值化网络在分类精度略有损失的情况下，可以大幅减少内存占用、提高计算速度，有利于移动端部署。

2 深度可分离卷积二值化网络模型

在本节中，构建了一个基础的深度卷积神经网络DCNN-8，并详细介绍了在DCNN-8的基础上采用的两种优化方法：深度可分离卷积和二值化网络。

2.1 构建深度卷积神经网络DCNN-8

深度卷积神经网络是最成功的深度学习算法之一[15]，作为一种有监督的学习算法，其无需人工对图像进行大量而复杂的特征提取，而是通过网络中的卷积运算提取特征，达到分类识别的目的，与传统机器学习方法[16]相比具有更强的特征学习能力和表达能力。

本文搭建的DCNN-8包含8个卷积层，2个最大池化层、1个特征融合层、2个全连接层和一个Softmax分类层，每一个卷积层的卷积核尺寸为5×5，且都包含批标准化和修正线性单元，具体的网络结构如图1所示。

图1 DCNN-8网络结构图

2.2 深度可分离卷积

深度可分离卷积(depthwise separable convolution)由逐通道卷积(depthwise，DW)和逐点卷积(pointwise，PW)两个部分组成，相比与标准的卷积操作，其参数数量和运算成本相对较低。

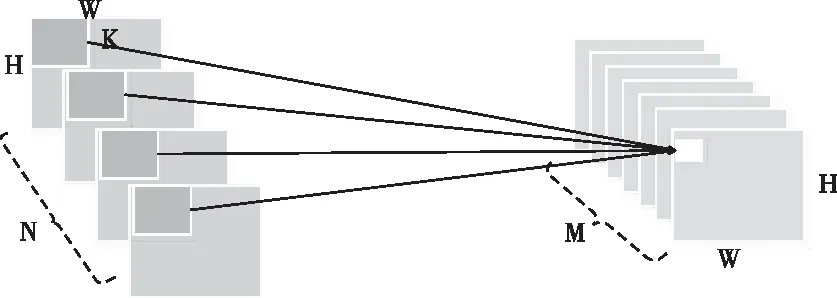
图2 标准卷积方式

图3 深度可分离卷积方式

图2、图3分别为标准卷积和深度可分离卷积，在标准的卷积操作中假设步长为1，大小为H×W×N的输入特征映射，生成H×W×M的特征映射，其中H表示特征图的高度，W表示特征图的宽度，N表示输入通道的数量，M为输出通道的数量。标准卷积由K×K×N×M的卷积核计算，其中K是卷积核的尺寸，所以标准卷积参数量为

Pc=N×M×K×K

(1)

深度可分卷积包括两层：逐通道卷积和1×1逐点卷积，其参数量如下

Ps=N×K×K+1×1×N×M

(2)

深度可分离卷积参数量与标准卷积参数量之比为

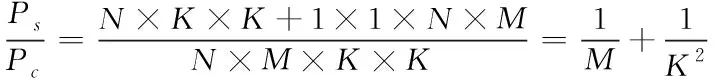
(3)

标准的卷积同时增强了空间相关性和通道相关性，而深度可分卷积首先增强空间相关性，然后增强了通道相关性。因此，使用深度可分离卷积，不仅可以对输入特征图进行有效的提取，保持网络分类精度，还大大减少了参数数量和运算成本。

在本文搭建的DCNN-8中，使用卷积核尺寸为5×5(K=5)的深度可分离卷积来代替传统的卷积，根据式(3)，采用深度可分卷积代替后，卷积层的总参数数量减少了10倍以上。

2.3 二值化网络

二值化网络(Binary neural network，BNN)被认为是将分类模型部署到资源有限的设备上最有前途的模型压缩方法之一[7]。

网络权重和激活值通过sign函数进行二值化，其值被限制为+1或-1

(4)

式中x为真实变量值，xb为二值化后的变量值。通过二值化，使网络权重和激活值的精度降低到1位，然后将32个二值化变量存储在一个32位的寄存器中，因此，二值化后的模型压缩比最大可以达到32倍。

在二值化网络的卷积层中，由于权重和激活值都被限制为+1或-1，因此可以用轻量级的按位同或(XNOR)操作和计算二进制串中1的数量(popcount)操作代替浮点型的复杂矩阵乘法运算

Xb*Wb=popcount(XNOR(Xb，Wb))

(5)

式中Xb和Wb分别为二值化后的激活值和权重矩阵。

二值化网络作为压缩算法中的极端情况，其拥有高压缩比、高加速比的性能优势，但是缺陷也较为明显。由于二值化网络将数值精度降低到+1或-1，卷积层输出的特征图很难携带足够的特征信息并保证输出值的范围适合下一层的二值化操作，如果直接使用sign函数对网络中传递的实数值进行二值化可能会导致特征图携带的特征信息过低，最终影响网络的分类精度，并且二值化网络在传播时采用的是±1，无法直接计算梯度信息，因此二值化网络一直缺乏有效的训练算法。针对以上问题，文献[17]中提出Rsign和RPReLu函数，通过使用可学习参数让网络学习到最适合的二值化阈值和激活值的分布，如图4所示，通过使用Rsign、RPReLu，缓解了二值化网络对于特征分布学习的困难，获得了良好的二值化特征，使网络的性能得到提高。

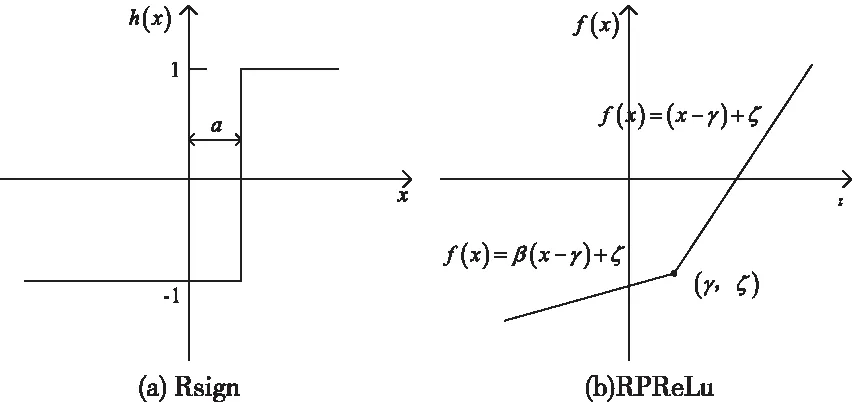
图4 Rsign和RPReLu函数

Rsign公式如下

(6)

RPReLu公式如下

(7)

式中xi是RPReLu在第i个通道的输入，βi是控制负部分斜率的可学习系数，γi和ζi是移动分布的可学习位移量。

针对经过深度可分离卷积处理的DCNN-8(SDCNN-8)，本文采用Rsign、RPReLu替换Relu激活函数作为二值化方法，如图5所示，将网络模型进一步压缩。

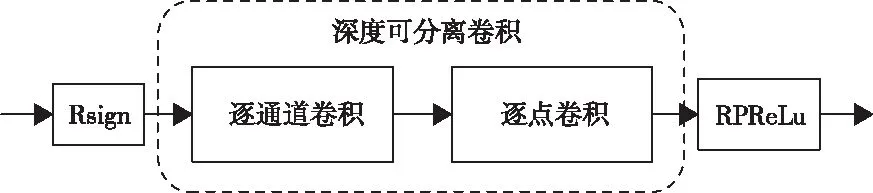
图5 二值化结构

本文为了弥补二值化导致的精度损失，通过实值教师网络来引导学生网络的训练，DCNN-8作为实值教师网络，学生网络即为经过深度可分离卷积处理的二值化DCNN-8(SBDCNN-8)。实值教师网络通过引入温度参数得到软化后的概率分布

(8)

式中T为温度参数，zi为softmax层输出的分类类别概率。若T越大，则概率分布越缓和，实值教师网络隐含的知识更容易被学生网络学习，此时学生网络的损失函数为

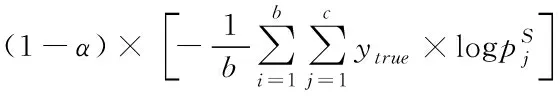
(9)

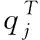
3 实验分析

3.1 实验环境与数据集

本文实验所使用的服务器配置及软件环境的配置如表1所示，实验在Windows10系统下运行，使用 NVIDIA GeForce GTX 1060和CUDA进行加速训练。

表1 实验环境配置

本文实验使用的数据集是由牛津大学Visual Geometry Group发布的公开数据集17flowers，其中包含了在英国比较常见的17种花，例如水仙，向日葵，洋甘菊等，如图6所示。数据集中的图像具有较高的空间复杂度和较大的类内差距，具体表现为数据集中的花卉图像具有多种形状、角度和光照条件。整个数据集共有1360张图片，每种花包含80张图片，选取其中60张图片作为训练集，20张图片作为测试集，并将图片尺寸统一缩放成128×128，便于网络输入。

图6 17flowers数据集

3.2 训练策略与结果分析

对SBDCNN-8使用两阶段式训练策略进行训练：第一阶段，首先在该训练集上训练DCNN-8，将预训练好的DCNN-8作为实值教师网络，然后对SBDCNN-8的激活值进行二值化、权重采用实值进行训练，共训练100轮；第二阶段，加载第一阶段保存的网络模型，并对权重进行二值化，然后继续训练。训练时超参数α设置为0.8，采用Adam优化算法，批大小设置为32，学习率设置为0.0005。

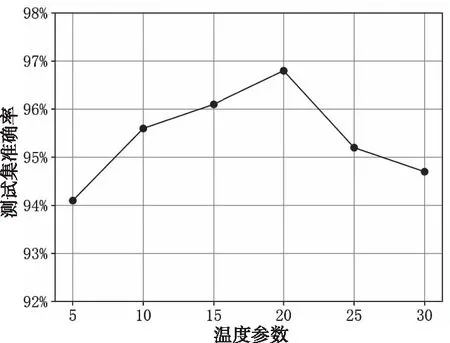
图6 不同温度参数下SBDCNN-8的平均测试集准确率

为了测试温度参数对于模型性能的影响，接下来在不同温度参数下对SBDCNN-8进行训练。当训练损失值达到最低并且稳定时终止训练，对测试集进行测试时温度参数设置为1，在每个温度参数下重复训练4次，取其平均准确率，如图7所示。当温度参数小于20时，随着温度参数的增加，测试集准确率逐渐上升，温度参数为20时，平均测试集准确率最高，达到96.6%。

为评估SBDCNN-8的性能，本文从权重位宽、激活值位宽、参数量、分类精度、内存占用以及计算时间等方面与DCNN-8和SDCNN-8进行对比。表2为不同网络模型的参数比较，SBDCNN-8的参数位宽仅为1位，参数量仅为8.4M。

表2 不同网络模型的参数比较

为公平的测试不同网络模型的分类精度，实验过程采用四折交叉验证。首先使用相同的训练集训练三种网络模型，SBDCNN-8和实值教师网络的温度参数设置为20，然后在同一测试集上进行测试，测试结果如表3所示。

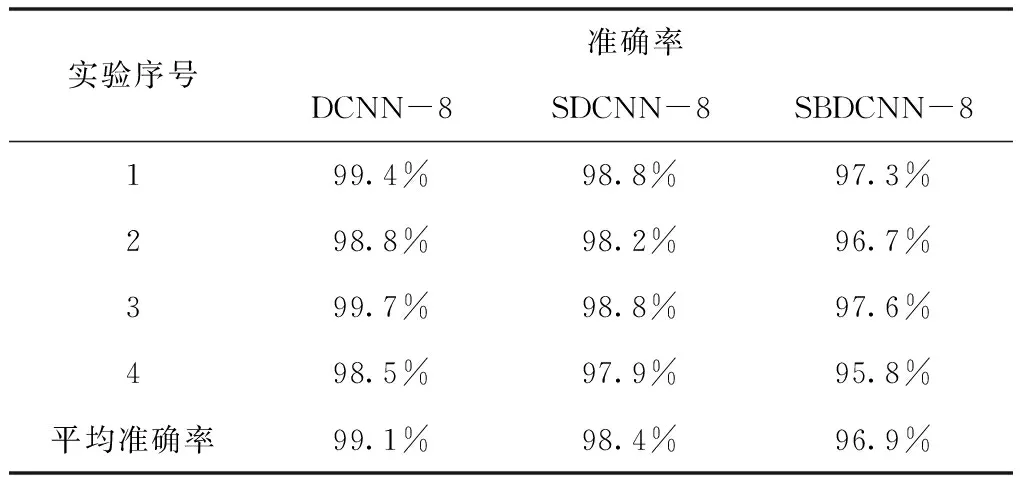
表3 不同网络模型的测试结果

从测试结果可以看出，全精度的实值网络DCNN-8的平均准确率为99.1%，SDCNN-8的平均准确率为98.4%，SBDCNN-8的平均准确率为96.9%，与实值网络相比，深度可分离卷积和二值化后网络的准确率下降约2.2%。图6为三种网络模型训练时的损失值曲线，反映了模型的训练进程，当迭代轮次达到150轮时，三种网络模型的损失值均达到平缓，其中DCNN-8的损失值最低，SBDCNN-8的损失值最高。

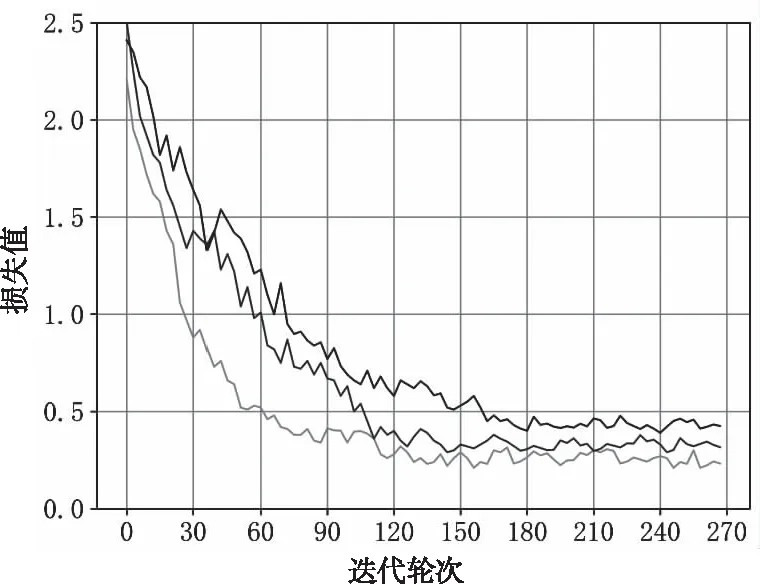
图6 不同网络模型训练时的损失值曲线

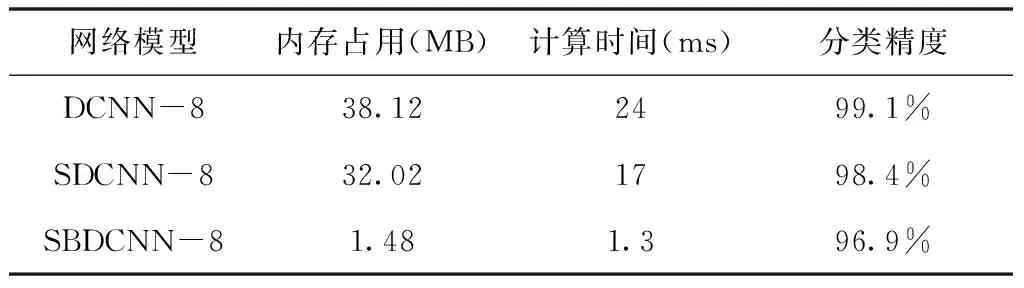
表4 不同网络模型的性能比较

表4为各个网络模型的性能比较，DCNN-8和SDCNN-8作为实值网络其分类精度较高，但是却消耗了大量的内存空间和计算时间，而SBDCNN-8在分类精度仅损失2.2%的情况下，内存占用相对于DCNN-8减少了25倍、计算时间节省了18倍，这对于部署在资源较少的移动端设备上尤为重要。

4 结论

本文提出一种基于深度可分离卷积二值化网络的模型压缩与优化加速的方法，通过深度可分卷积代替标准卷积并对网络进行二值化，大幅减少了内存占用和计算时间。通过实值的教师网络引导训练，避免了网络二值化后分类精度的大幅下降。在下一步工作中，将继续对模型压缩和优化加速方法进行研究，并将本文提出的方法移植到资源有限的移动设备上，实现硬件部署。