施工升降机多电机同步控制系统建模与仿真
2023-03-29赵秉鑫张豪臻
卢 宁,赵秉鑫,张 昊,张豪臻
(1. 北京建筑大学机电与车辆工程学院,北京100032;2. 北京市建筑安全监测工程技术研究中心,北京100032;3.北 京理工大学宇航学院,北京100081)
1 引言
施工升降机在建筑行业应用广泛,其作为主要的起重运输机械,对运输效率以及施工人员乘坐的舒适度都具有一定的要求[1]。目前,齿轮齿条式施工升降机市场占有率较高,其驱动系统一般由两台或三台大功率电机组成,随着变频技术的发展,传统的继电器与接触器的开关控制方式逐步被变频控制方式所代替,大多数升降机采用一个恒压频比调速方式的通用变频器拖动三个异步电机的控制系统,由于升降机工作环境复杂、传动机构存在非线性因素以及各个电机结构参数存在差异,该控制系统导致多台电机实际转速不同步,最终降低升降机平层精度,影响升降机的运行效率[2]。因此,对于这种重载运输设备,在面对外部负载不断变化的工况,提高多电机的同步控制精度显得尤为重要。
常用的多电机同步控制策略主要包括并联控制方式、主从控制方式、交叉耦合控制方式、偏差耦合控制方式和均值耦合控制方式等[3]。其中采用并联和主从控制方式虽然结构简单,但同步性能差,适用于控制精度不高的场合;相邻交叉耦合对三台以上电机进行同步控制时,运算量小,但受到扰动的电机对周围电机的影响逐级递减[4];偏差耦合通过计算系统中任意两部电机的同步误差的差值乘以不同的补偿系数,进而确定补偿量,提高同步控制精度[5];均值耦合控制利用各个电机跟踪误差信息完成对转速补偿量的计算,应用于电机数量较多的场合[6]。
为了解决常规同步控制策略存在的问题,国内外学者做了大量的研究,已有许多现代控制方法应用到电机同步系统当中,例如自适应控制[7]、模糊控制[8]、神经网络[9]、滑模控制[10]等。滑模控制因其结构简单,鲁棒性强等特点在同步系统中应用广泛。文献[11]提出了一种偏差耦合结构与非奇异终端滑模控制相结合的控制方法,同步精度得到提高;由于非奇终端滑模控制在系统初始状态与平衡点较远时收敛速度较慢,文献[12]提出一种混合非奇异终端滑模控制,提高了收敛速度,但其收敛时间的值取决于控制器参数和系统初始状态;为此文献[13]提出一种固定时间终端滑模控制方法,使得系统收敛时间不受初始状态影响,应用广泛。
为了进一步提升同步控制系统的控制精度,本文改变施工升降机原有的控制方式,采用三个矢量变频器分别控制三个电机的控制结构,并且提出一种分段非奇异固定时间终端滑模控制方法,针对传统偏差耦合控制器进行改进,使得改进后的控制器能够在固定时间内对跟踪误差和同步误差完成收敛。采用ADAMS与MATLAB联合仿真的实验方法,模拟施工升降机的实际运行工况,对改进的同步控制器进行了仿真。
2 系统描述
2.1 偏差耦合同步控制策略模型
偏差耦合控制结构原理是利用每台电机跟踪误差信息和各个电机之间的转速同步误差信息,来确定对每台电机转速的补偿量,进而实现多电机的同步控制。该结构主要包括电机跟踪误差控制模块和电机同步误差补偿模块,通过两个模块的共同作用,最终将各个电机在过渡周期和转矩扰动时的相对速度归零,达到系统的控制目标。以本本文研究的施工升降机多电机同步控制系统为例,其结构示意图如图1所示。
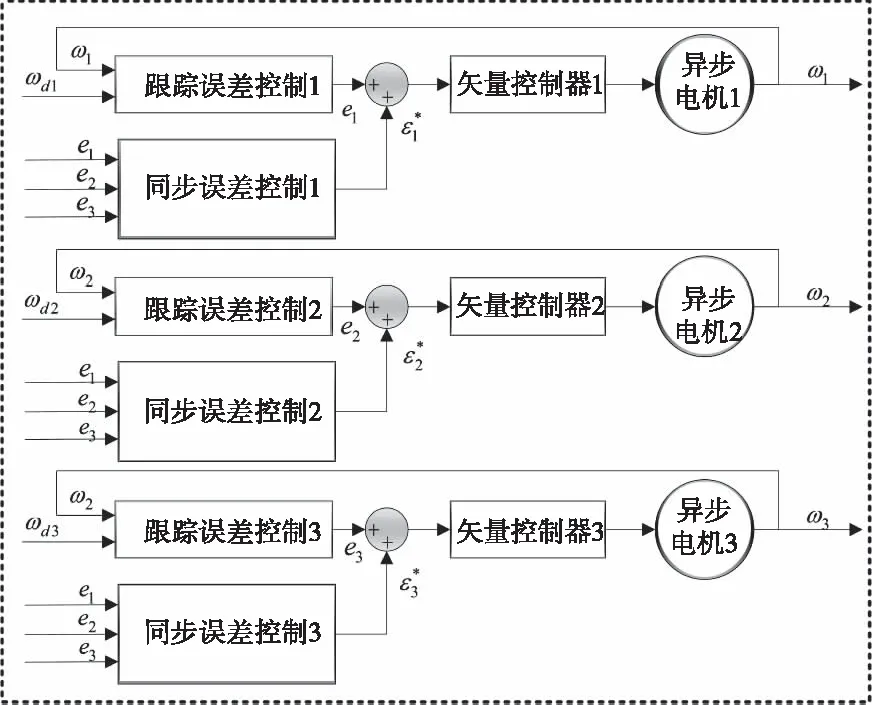
图1 多电机偏差耦合控制结构图
其中每台电机的同步误控制器的补偿量是通过求取1台电机与其它电机之间的同步误差乘以固定的增益后得到。补偿增益通过计算电机之间转动惯量的比值确定。其结构示意图如图2所示。

图2 同步误差控制器结构图
ei=ωd-ωi
(1)
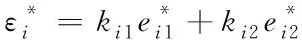
(2)

2.2 三相异步电动机的数学模型
为了简化分析,在建立三相异步电机数学模型时,作如下处理:忽略空间谐波,所产生的磁动势在气隙空间分布为正弦波;忽略定子铁心饱和,各绕组的自感和互感为定值;电机磁路线性,电感参数为定值;忽略磁路饱和以及铁心损耗[14]。采用按转子磁链定向控制方式,在M-T旋转坐标系下的状态方程如下
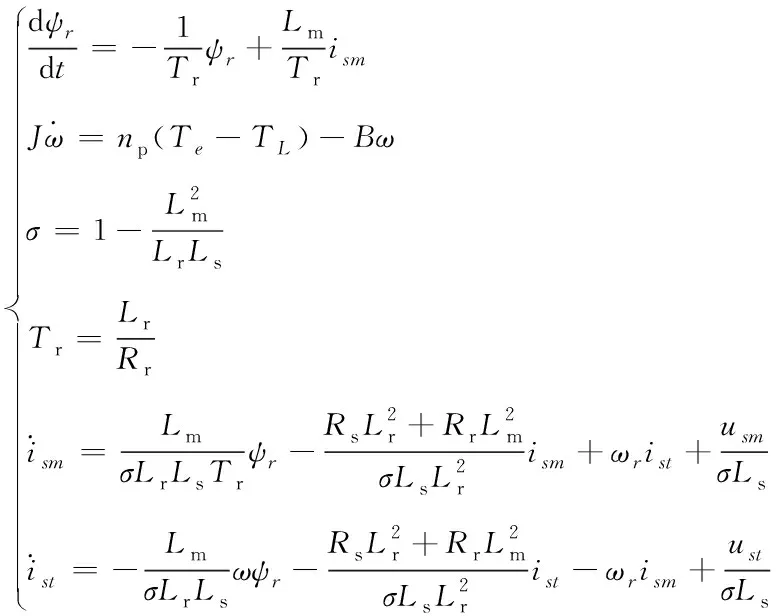
(3)
式中:Te—电磁转矩;np—磁极对数;Lm—定子与转子等效绕组间的互感;Lr—转子等效自感;ψr—转子磁链;ist—定子电流T轴分量;ism—定子电流M轴分量;J—电机转动惯量,Ls—定子等效自感;Rs—定子电阻;Rr—转子电阻;ω—转子机械角速度;ωr—转子电角速度;usm—定子电压M轴分量;ust—定子电压T轴分量。
得到电磁转矩表达式

(4)
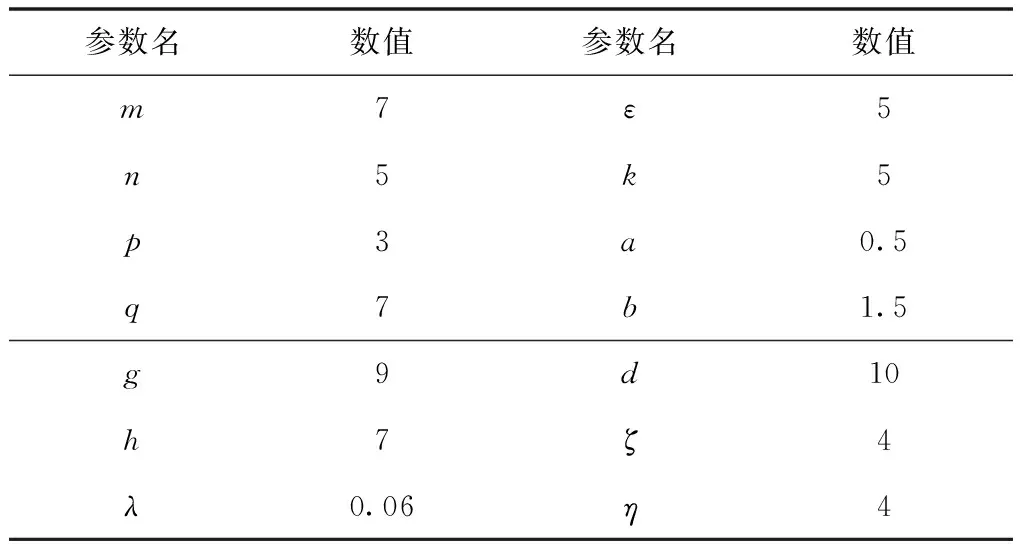
本文参考某厂家的SC200施工升降机的电机型号和传动机构的相关参数,由于同一批次生产的电机各个参数差异不大,故选用的三台异步电机的参数均相同,体参数如表1所示。
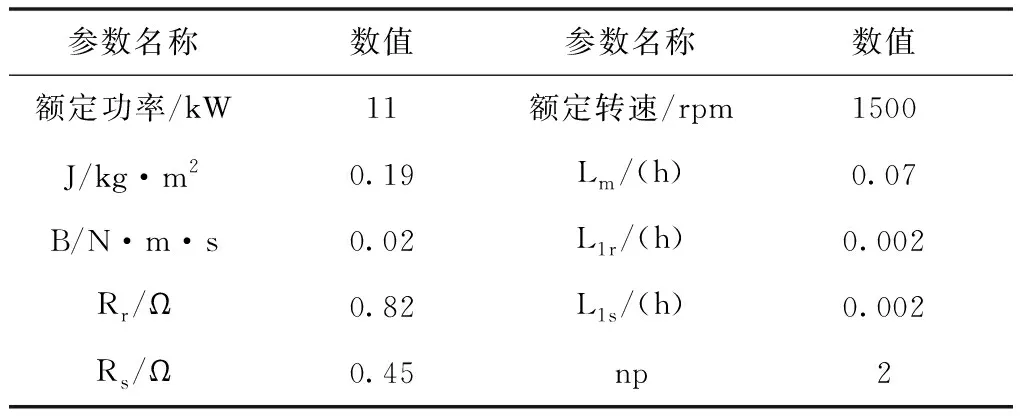
表1 异步电机参数
3 跟踪误差滑模速度控制器设计
针对传统的非奇异终端滑模结构能够在有限时间内令控制系统收敛到期望轨迹,并避免了控制奇异区域,但是当系统初始状距离平衡点较远时,收敛时间过长[15];传统的固定时间滑模结构能够在固定时间内令控制系统收敛到期望轨迹,即收敛时间与控制器结构参数有关,与系统的初始状态无关,但是当系统接近平衡点时,存在控制奇异区,且收敛时间较长的优缺点[16]。为了提高系统的动态特性和鲁棒性,本文提出了一种分段固定时间非奇异终端滑模速度控制器。
整理得到
取系统状态变量为
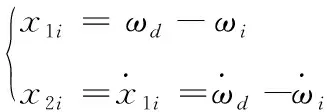
(5)
式中:ωd—电机给定转速;ω—电机实际转速。
由(3)(4)(5)式联立可得
高中阶段的学生思维异常活跃,并敢于提出不同的讲解与想法,特别是一些启发性的问题,他们是乐于思考并善于思考的。所以,在高中数学课堂教学中,新课程的导入期间,教师需为学生创设良好的问题情境,以让学生课前集中其全部注意力,并能开起其思维的闸门,让学生的求知欲和探知欲得到深化,进而能让学生的学习状态由原来的被动学习转为主动学习,进而能在和谐的学习氛围中进行数学知识的学习。
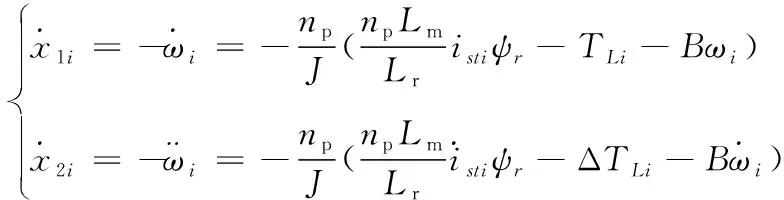
(6)
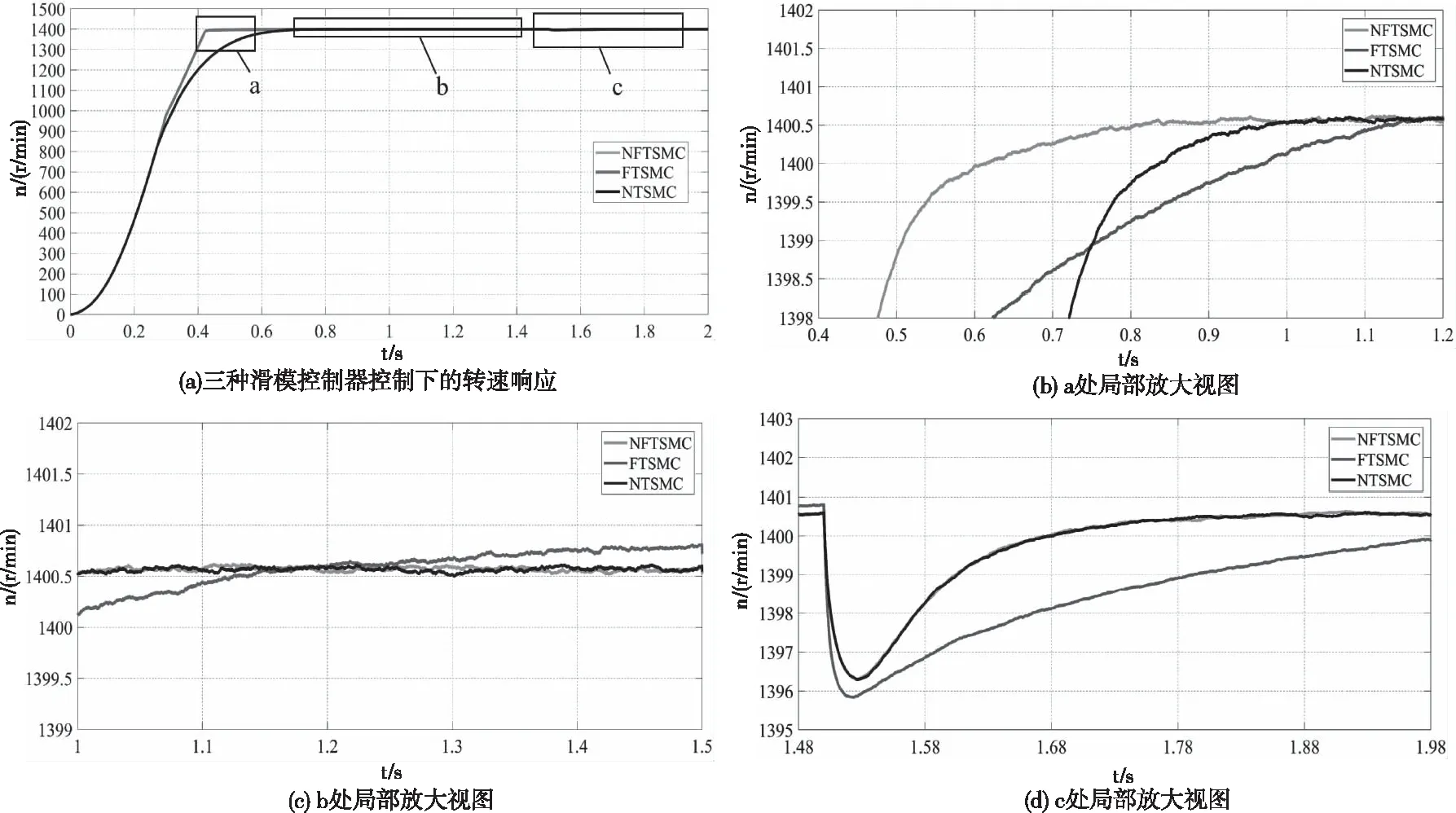
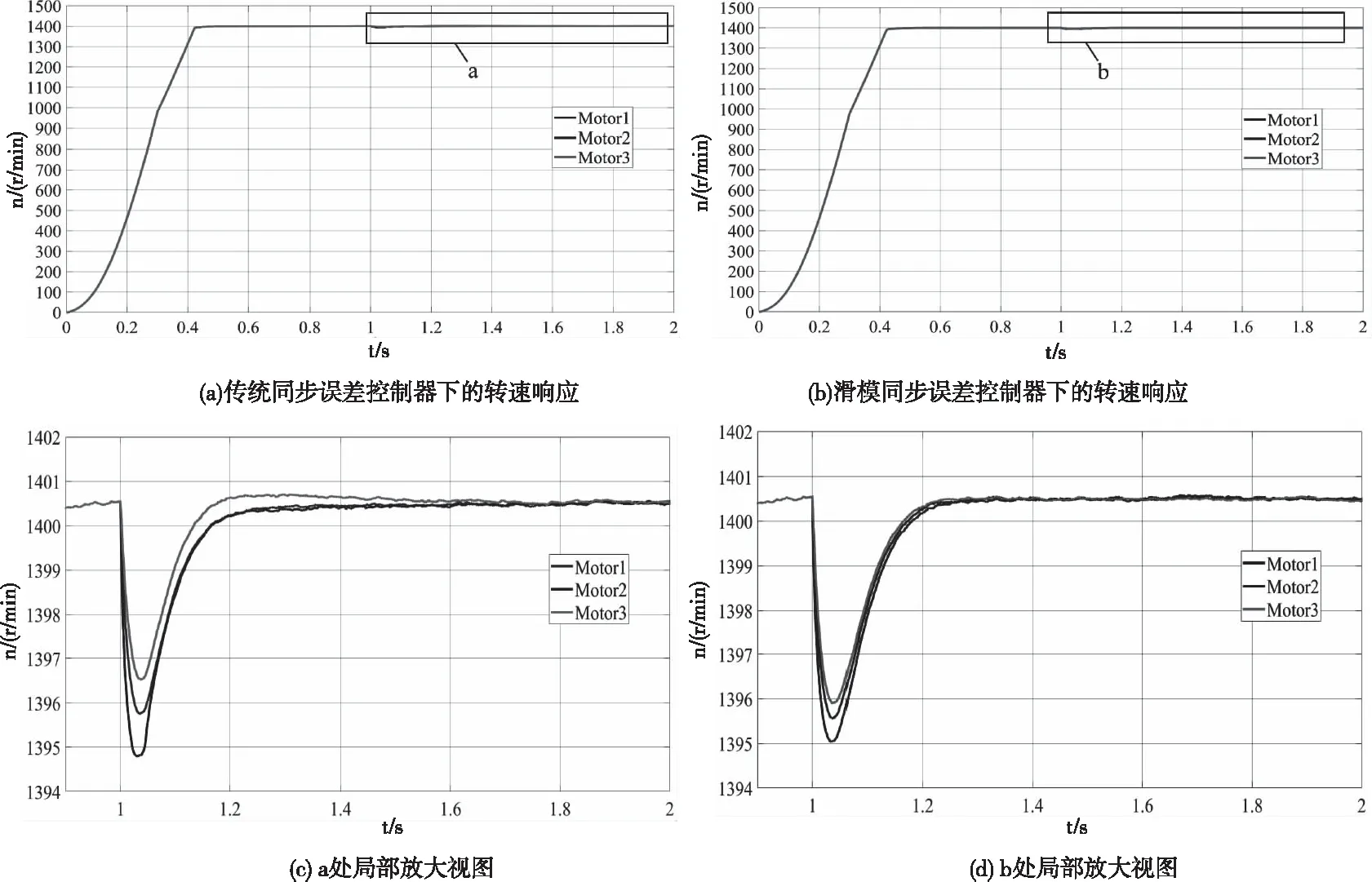
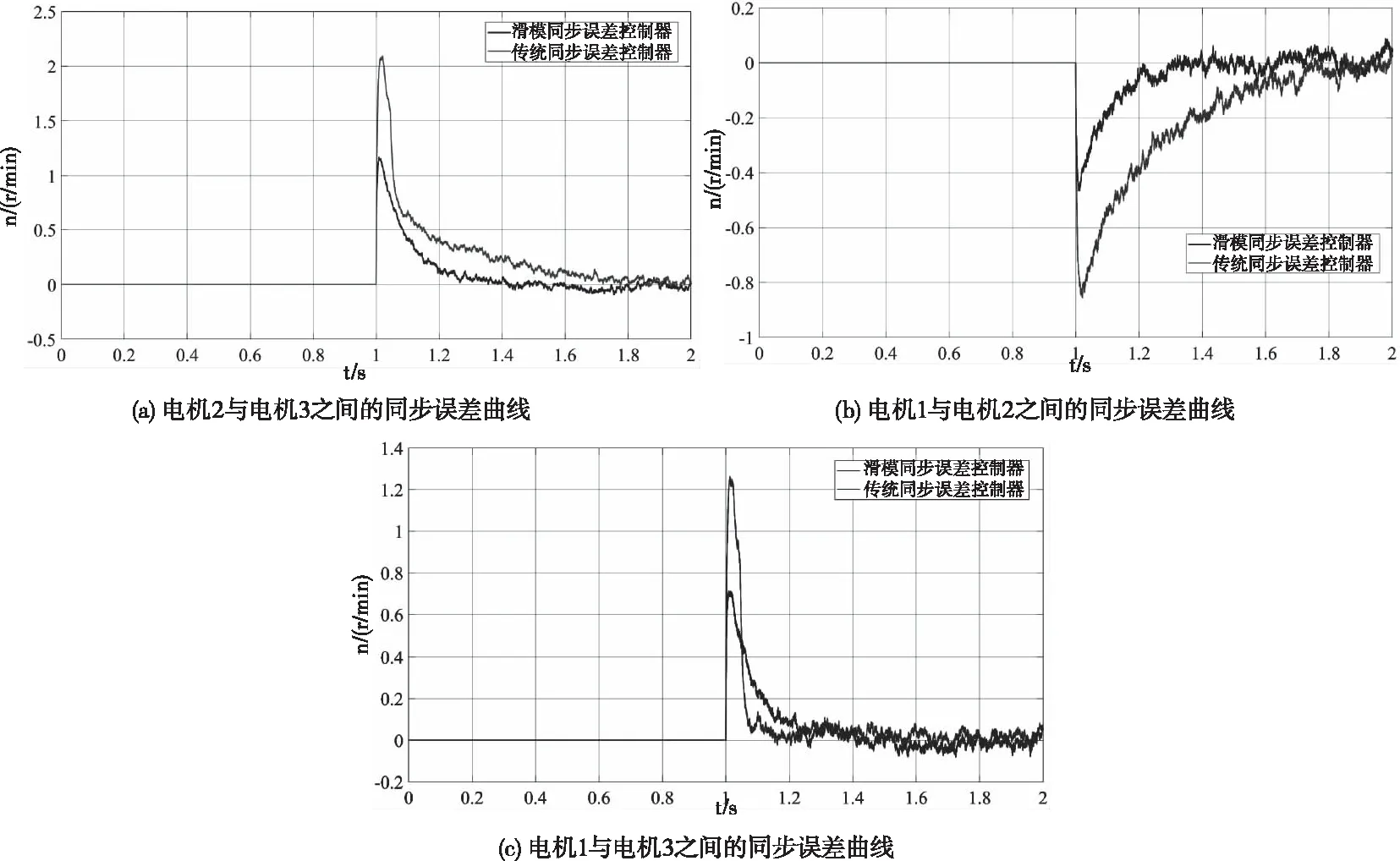
本文主要研究施工升降机运行过程中由与负载变化引起电机不同步的问题,故将TLi视为不确定项即外部扰动,根据现实情况ΔTLi不可能无限大,满足|ΔTLi| 本文设计的分段滑模面为 经分析可知,在|x1|>5,滑模面为s1i,当系统状态距离平衡点较远时,具有较快收敛速度;在|x1|≤5,滑模面为s2i,当系统状态距离平衡点较近时,具有较快收敛速度,滑模面和及其导数不含负指数项,避免了奇异发生。由式(11)(12)可知,系统控制量经过了积分滤波器,削弱了抖振现象,有效抑制系统稳态误差。 师:请同学拿出学具袋,同桌选一位代表,老师说出一个几何体的名称,请你从袋子中摸出它的模型,举起来,然后我们请摸的最快的同学说说你是怎么摸到的. (7) 其中,当|x1|≤1时,s1=0,当|x1|>1时,s2=0。 对滑模面s1i和s2i分别进行求导可得 (8) 仿真过程为,设定目标转速为1400r/min,当电机运行稳定时,在1.5s时电机负载从50N·m增加到55N·m,仿真对比结果如图7所示。 (9) 为了削弱抖振的影响,保证趋近模态有良好的动态品质,趋近率选为双幂次趋近率[17]: (10) 式中:di、εi、ki、a、b为大于零的整数,且0 故可得控制率u1i、u2i与ui分别为 (11) 阿里认真地自言自语,如同平常跟母亲说话。阿东隐忍不住,眼泪哗哗地流了出来。他把自己的头蒙在被子里,恐怕阿里听到他的呜咽。 推荐理由:本书试图构建一个分析思考的理论框架,以兼收并蓄的融合视角探讨新时代下“中华传统的道德与和谐、西方文明的科学与理性、社会主义的理想与奉献”三源合流的可能性及逻辑基础。作者从文化理念的深层角度,对当下如何走出迷茫,依靠何种“定力”实现民族的伟大复兴进行了探究。 (12) isti=ist1i+ist2i (13) (4)三叠系。测区三叠系仅出露下统的一部分,分布于东流—三门江林场以东以及柳城凤山向斜东端一带,面积约19.13 km2。岩石地层单位为罗楼组(T1l)。 定理1 对于系统(9),使用本文设计的固定时间非奇异终端滑模面(7),选择趋近率(10)和控制率(13),则系统状态x1i,x2i可以在固定时间内到达平衡点,收敛时间只与控制器参数有关的上界 无独有偶,广东清远农村最近几年进行农村综合改革,其中有两项特别重要,一项是土地整合,一项是资金整合,两项改革的重点都是恢复村庄集体权力,前者是恢复村庄集体对土地的权力,后者试图将国家转移给农户的农业综合补贴通过农户转让形式集中到村社集体手上办大事,这个大事就是解决单家独户不好办、办不好和办起来不划算的公共事业。清远市农村综合改革的试验证实,土地整合和资金整合可以大幅度提高村社集体的能力,使村社集体有能力对接国家资源,并以此资源来回应农户需求。 T≤Tmax=Ta+Tb (14) 引理1[18]:对于一类系统 所谓线上线下“双师课堂”,即由一位名师通过视频在线上直播自己的讲课,而在线下的实体课堂里还有一位辅导老师负责在现场为学生答疑解惑。[2]这种课堂并不完全都是两个教师的“1+1”模式,多数情况下是“1+N”模式的,即一个名师线上上课,同时有N个线下实体课堂在学习该课程,N个线下课堂里配备N个辅导老师进行现场辅助教学。 (15) 其中满足ζ>0,η>0;m、n、p、q均为正奇数并且满足m>n,q>p,那么式(15)的平衡点是固定时间稳定的,且收敛时间T有界,满足如下关系: (16) 引理2[19]:对于一类系统 (17) 本文采用机电联合仿真的方法进行仿真。在MATLAB/Simulink中搭建跟踪误差控制器和同步误差控制器的的仿真模型。 (18) 证明: 令s1i=0,s2i=0求解式(7)可得 (19) (20) 式中x1i(0)—初始时刻的系统状态;x1i(t1)—系统状态x1i=5时刻的状态;x1i(t2)—系统状态x1i到达平衡点时刻的状态。 《爵士乐》还戏拟了传统小说的大团圆的结局,这部作品没有像一般的后现代作品那样,采用开放式的结尾,给读者以想象的空间,使读者陷入迷惘、失落的情绪之中,这部作品的大团圆结局让读者在回味悲惨的人物命运的同时,感到一丝欣慰和满足。文本在外部形态上承袭了大团圆叙事成规的主要特点,在内部构成上也具有它们的某些构成要素,叙述也基本按照读者预期的程序展开,而在这一系列的一致背后,其深层意义却是要对所戏拟的叙事成规的传统意旨进行瓦解,或者说要对已成惯例的审美情感与观念倾向进行颠覆与否定。至此,小说中所表现出的鲜明的后现代叙事策略形成了对传统现实主义文本大团圆结局的戏拟。 对式(19)和式(20)求和可得 Ta=T1+T2 问题2:道观或寺庙里常常有抽签算卜一说,一个桶里放着若干竹签,竹签上刻着“上”“中”“下”等字样,每根竹签上还刻有号码,善男信女们拿着桶摇晃,直到桶里掉出一根签来,然后拿着掉出来的竹签去找道士或和尚.道士或和尚根据竹签上的号码找到对应的签诗,那首签诗里便“隐藏着”你或你关心的人的祸福.道士或和尚根据签诗为你解卜,回答你所关心的事情的吉凶.这是唯心主义的东西,不过是给人心理上的某种慰籍,自然信不得.但可以探讨一下抽签过程中所蕴含的数学原理,你能用数学方法描述一下这个过程吗?例如签桶里的签是什么?摇桶的过程可以作何解释?竹签掉出来说明了什么? (21) 由式(21)可知,系统在滑模面s=0上到达平衡点收敛时间是固定的。 =s[-εi|si|asgn(si)-(di+ki)|si|bsgn(si)] =-εi|si|a+1-(di+ki)|si|b+1 (22) 根据引理1得 (23) 由式(23)可知,系统状态到达滑模面si=0上趋近时间是固定的。 故系统收敛间总时间为T 注1系统的收敛时间上界T取决于所设计的滑模面参数而与系统初始状态无关。合理的选择控制器的参数可以调整系统的动态响应特性和稳态跟踪精度。 参考跟踪误差控制器的设计,设计第i台电机的同步误差控制器的滑模面如下 雪萤把记事本及U盘放进手提包,迅速下楼,并掏出手机,准备拨打110。楼梯口,突然出现两个戴墨镜的青年。她想绕过去,那两个男子却故意阻住了去路。手机掉在地上,她大叫救命,转身就跑。其中一个男子迅速冲上来,捂住她的嘴,另一个把她的手反扭到身后绑起来。 (24) (25) (26) 为管理会计发展提供法律与制度保障。所以,加快相关的法律规章制度迫在眉睫。杜绝一切违法违章行为。同时,我们需要明确,仅有法律规范是不够的,还应该加强内部控制的设计与实施。当前管理会计的前景十分广阔,所以更应该规范职能,提高工作的效率。借助网络媒体平台,强化对大数据的认识,突破固有的模式,更新新技术。加强对专业型人才的培养。促进各个行业的融合发展。促进企业朝着可持续的方向发展。随着大数据时代的发展,管理会计将对企业的发展起到更加重要的作用,为企业的发展提供有力的保障。 (27) (28) 根据现实情况扰动项ΔTLi不可能无限大,满足|ΔTLi1| (29) 则第i台电机的同步误差控制器的控制率为 (30) 第i台电机的总控制率为 (31) 注2:由定理1可得,任意两台电机之间的同步误差收敛至平衡点的时间上界均与系统初始状态无关,因此跟踪误差和同步误差均在固定时间内收敛,与系统的初始状态无关。 其中λ、g、h均为大于0的常数,且g、h为奇数,1 单台电机跟踪误差控制器的结构图如图3所示。 图3 单台电机跟踪误差控制器仿真模型 单台电机同步误差控制器的结构图如图4所示。 图4 单台电机同步误差控制器仿真模型 针对跟踪误差和同步误差滑模速度控制器参数的经过多次实验对比分析,综合考虑系统的超调量、调节时间以及稳态误差,最终选取跟踪误差滑模控制器和同步误差滑模控制器的参数如表2所示。 表2 控制器参数 为了得到符合实际工况的仿真结果来验证上述控制器的控制效果,在ADAMS中建立施工升降机传动机构的动力学模型,通过ADAMS/Controls接口模块建立与MATLAB/Simulink的数据交换。其中,动力学模型如图5所示 图5 施工升降机动力学模型 将MATLAB/Simulink中的电机转速作为输入变量,将ADAMS中各个电机的负载力矩变量和齿轮轴的转速变量作为输出变量,反馈至电机矢量控制系统模型中,进而构建完整的闭环控制系统。联合仿真模型框图如图6所示。 图6 多电机同步控制系统联合仿真模型 首先进行单电机跟踪误差控制器的对比仿真,将本文提出的分段滑模速度控制器(NonsingularFixedTimeSlidingMode,NFTSMC)分别与传统固定时间滑模控制器(FixedTimeSlidingMode,FTSMC)和传统非奇异终端滑模控制器(NonsingularTerminalSlidingMode,NTSMC)进行对比分析,三个控制器均采用双幂次趋近率,其中各个控制器的参数均与表4相同。 图7 系统启动与突增负载时的动态响应仿真结果 由图7可以得出如下结论: 1)在系统启动过程中,根据图7(a)可知,采用FTSMC的调节时间为1.2s,响应时间较长,采用NTSMC的调节时间为0.1s,响应时间中等,采用NFTSMC的调节时间0.8s,响应时间最短。 (1)有效性原则。在制作、使用课件时,必须从实际出发,注重实效。工具使用不在于多而在于精,恰当运用多媒体,找准最佳作用点,有的放矢,才能起到画龙点睛的作用。 2)在系统从启动到稳定运行过程中,根据图7(b)可知,采用三种控制器的转速超调量几乎为0,采用NTSMC和NFTSMC的稳态误差一致,并且小于采用FTSMC的稳态误差。 上述处理剂分别为天然高分子包被抑制剂、降滤失剂、封堵抑制剂和润滑抑制剂。根据优选出的环保处理剂,开展配伍性实验,形成了120℃环境友好型钻井液体系,配方为(以质量分数入场,下同):3%~5%膨润土+0.3%~0.5%天然高分子包被剂HV-500+0.8%~1%LV-PAC+1%~2%聚合醇+1%~2%聚醚多元醇+1%~2%白沥青+1%~1.5%改性淀粉。 3)在对运行稳定的系统突然施加负载的过程中,根据图7(c)可知,采用NTSMC和NFTSMC的超调量和调节时间一致,分别为0.27%和0.24s,受到负载干扰影响较小,采用FTSMC的超调量和调节时间分别为0.36%和0.48s,受到负载干扰影响较大。 综上,针对不同滑模速度控制器的仿真结果验证了,在x1的初始状态距离平衡点较远时,FTSMC的收敛速度明显大于NTSMC,在x1的初始状态距离平衡点较近时,NTSMC的收敛速度明显大于FTSMC。文本采用的NFTSMC结合了FTSMC和NTSMC的优点,且在固定时间上界2.33s之内实现了对跟踪误差的全局快速收敛。 其次进行多电机同步误差控制器的对比仿真,将本文提出的滑模同步控制器(SlidingModeSynchronousController,SMSC)和传统偏差耦合同步控制器(DeviationCouplingStructureSynchronousController,DCSSC)进行对比分析,其中同步系数β=1,根据电动参数表1,确定DCSSC的增益参数k11=k12=k21=k23=k31=k32=1。 仿真过程为,设定三台电机的目标转速均为1400r/min,当三台电机达到各自稳定运行状态后,在1s时,电机1的负载从50N·m增加到55N·m,电机2的负载从50N·m增加到60N·m,电机3的负载从50N·m增加到52N·m。仿真对比结果如图8和图9所示。 由图8和图9可以得出如下结论: 1)在对运行稳定的系统突然施加负载的过程中,对比图8(c)和(d)可知,采用SMSC的系统使得3台电机几乎同时恢复到目标转速,受到负载干扰影响较小,而采用DCSSC的系统电机2与电机3调节时间相同,电机1的调节时间较长,受到负载干扰影响较大。 2)根据图9(a)可知,采用SMSC电机2与电机3的最大同步误差与采用DCSSC相比减少了46%,调节时间减小了23%;根据图9(b)可知,采用SMSC电机1与电机2的最大同步误差与采用DCSSC相比减少了44%,调节时间减小了23%;根据图9(c)可知,采用SMSC电机1与电机3的最大同步误差与采用DCSSC相比减少了48%,调节时间增加了1%,各个电机之间的同步误差均在固定时间上界2.33s之内实现了全局快速收敛。 综上,采用SMSC在同步性能上优于DCSSC,在受到扰动时,同步精度高,具有良好的鲁棒性。 图8 传统同步误差控制器与滑模同步误差控制器在突增负载情况下的动态仿真结果 图9 传统同步误差控制器与滑模同步误差控制器同步误差曲线 1)本文对施工升降机多电机同步控制系统,提出了一种分段非奇异固定时间终端滑模控制方法,应用到跟踪误差控制器和同步误差控制器中,能够使系统的滑模变量、跟踪误差和同步误差均能在固定时间内收敛,且收敛时间上界与系统初始状态无关,只与控制器设计参数有关。 2)本文采用了机电联合仿真的方法,对提出的控制方法和传统控制方法进行仿真对比验证。研究结果表明,相较于传统控制方法,该控制方法能够在系统启动阶段提升系统的动态性能,当系统受到扰动时具有更高的同步精度,提高了系统的鲁棒性,实现了3台电机的同步控制。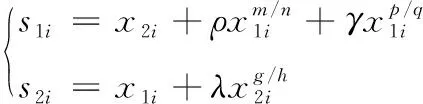
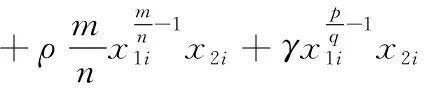


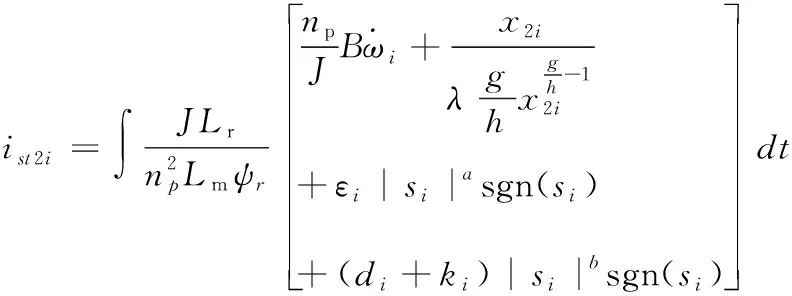


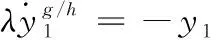
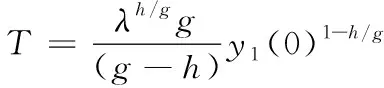
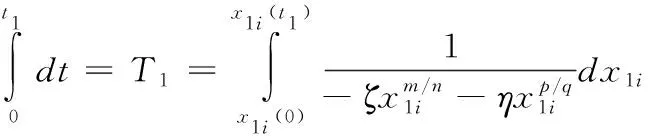
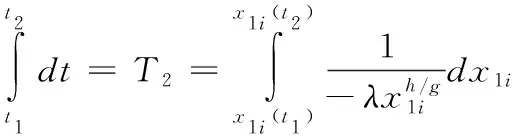

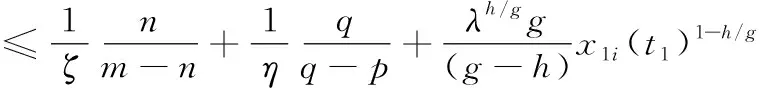
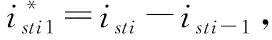
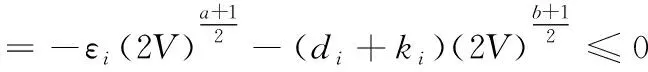

4 同步误差滑模控制器设计
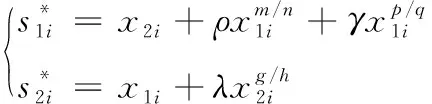
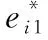


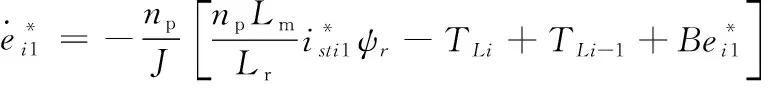
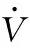
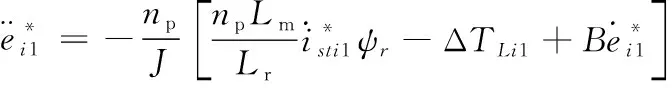
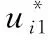


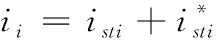
5 仿真与分析
5.1 建立联合仿真模型
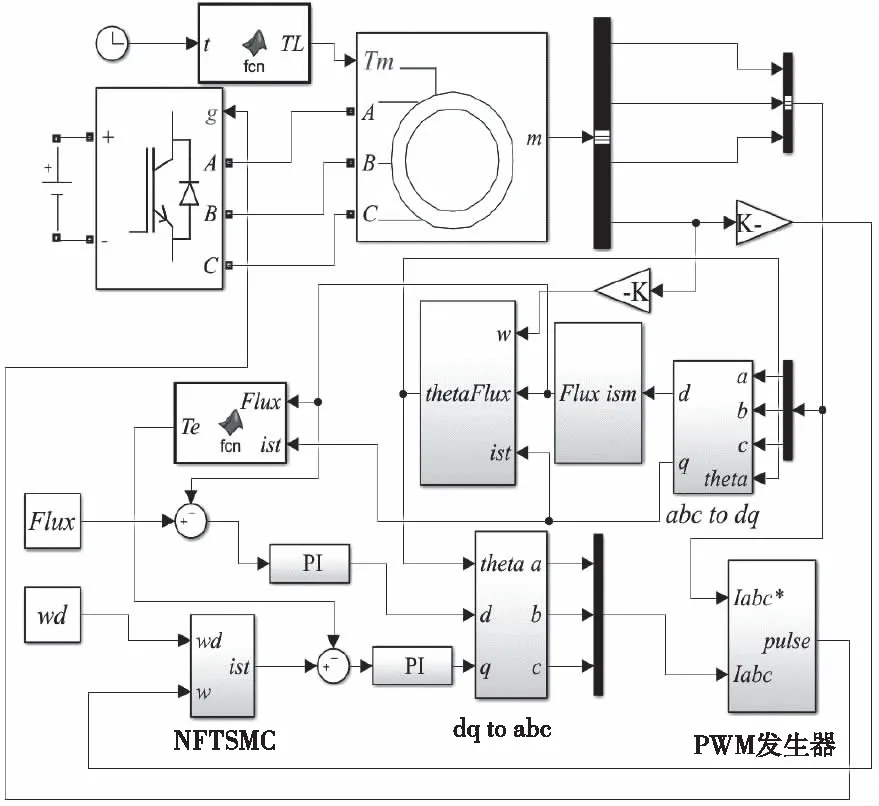


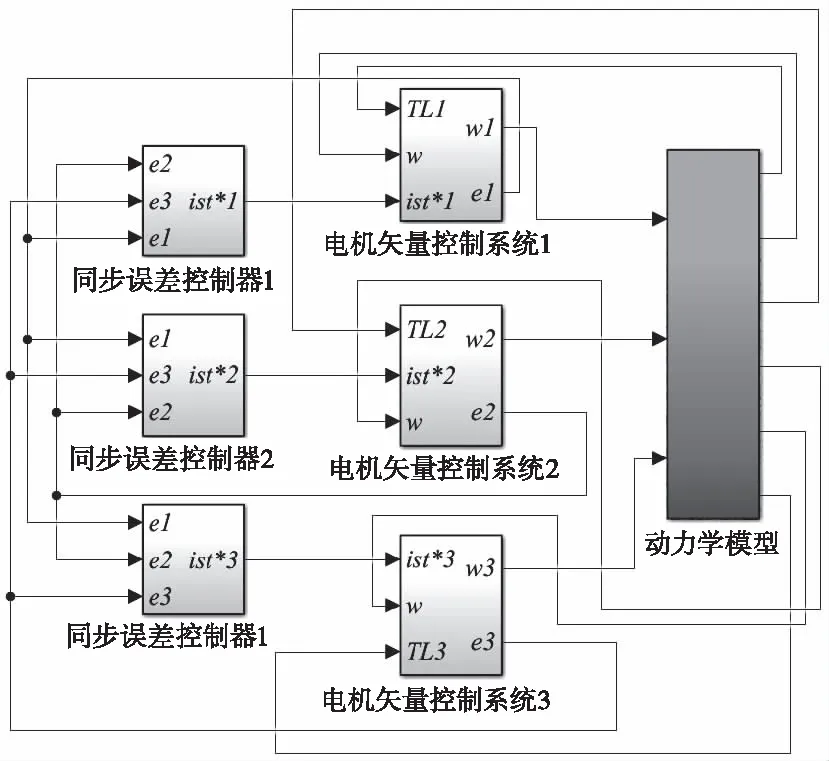
5.2 仿真分析
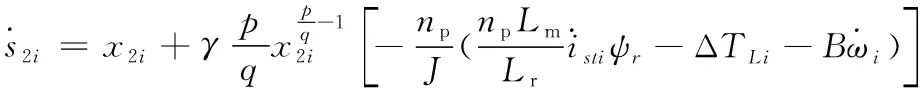
6 结束语
