基于数据量化分析的动态视觉景观规划仿真

刘晓青，芮 潇

(东南大学成贤学院，江苏 南京 210088)

1 引言

景观一般可以理解为某地区的综合特征，其中包括人文、经济以及自然等方面[1]；一般的自然综合体：主要是指地理各要素间互相联系，互相制约、采用有规律结合所形成的内部一致整体，分为不同等级区域或者是类型单位；区域概念，作为个体区域单位，就是相当于综合自然区域等级系统内最小的一级自然区，是对应一致发生与形态结构同一个区域；类型概念主要是用来分类任何区域单位，即指互相合理地段按照外部特征类似性，将其归成相同类型单位，例如森林景观、草原景观等[2]。

景观规划主要是指区域范围内完成景观规划，从区域基本属性以及特征出发。其中设计规划都包括：大众行为心理主要从人类心理精神感受出发，依据人类在环境内的行为心理以及精神活动规律，采用心理文化引导，设计出令人积极向上、浮想联翩以及赏心悦目的景观；环境生态则是随着现代环境的意识运动发展，从而深入景观设计规划的内容，依据自然界内生物学原理，采用人工材料、水体、土壤、动植物、阳光以及气候等，设计规划出舒服良好的物理环境；而视觉景观则是从人类视觉感受出发，通过实体空间景观和美学规律，创造出赏心悦目的环境形象。这三种元素对于景观感受起到的作用是密不可分、相辅相成的，采用以视觉为主的感受通道是借助与景观环境的形状，从而在心理引发触景生情、心旷神怡等效果[3]。

景观设计规划还要以做到保护资源节约资源、尊重自然显露资源和以人为本的体现博爱等原则。因为景观设计规划较为繁琐，如果只是通过语言叙述，可能会出现设计者理解错误、叙述不清等情况发生，很难获得系统性设计，这样很有可能导致在进行规划时出现偏差，甚至是失误。所以需要通过数据量化分析的方式，进行系统整理，使其更加严谨。为此本文提出一种基于数据量化分析的动态视觉景观规划仿真方法，能够很好保护景观生态环境，降低空气污染。

2 数据量化分析算法下景观空间参数计算

2.1 景观空间格局指标

空间格局分析法主要是用来研究空间配置关系与景观构造组成特征的分析方法，对于景观空间格局和异质性的定量描述是对景观过程、功能以及结构分析的基础。在通过异质性与格局将景观的时间过程以及空间特征相连接。即可分析与描述景观的规律性[4]。

而景观格局通常是指很多景观过程长期作用产物，可以直接影响景观过程，而不同的景观格局对于景观生态系统、种群或者是某个个体作用较大。具体计算方法如下所示：

1)人均绿地的面积MG，具体公式为

MG=Ai/P

(1)

式中：Ai代表绿地系统内i类景观面积，P代表所在地区人口。

2)绿地率G0，具体公式为

G0=Ai/S×100%

(2)

式中：S代表研究区域的总面积[5]。

3)多样性的指数为H，其数值大小能够反映出各景观要素占据的比例变化以及景观要素多少。在景观利用单一要素所构成时，则景观为均质的，多样性的指数即为0；而利用两个以上要素所构成的景观，在景观类型占据的比例相等时，那么景观多样即为最高，导致各个景观的类型占据的差异比例增大，具体计算公式为

(3)

上式中：H代表某地区景观的多样性指数，Pi代表此地区各个景观面积以及此地区总面积比，m代表此地区内景观类型个数。

4)优势度指数代表景观多样性以及最大多样性偏离的程度，或者叙述景观是由少数几个重要景观类型所控制的程度，其优势度指数越大，那么说明偏离的程度就越大，组成各景观的类型占据点的比例差异越大，或者说某种或者少数景观种类占据优势；而优势度越小就越表明偏离的程度越小，组成景观的各种类占据比例几乎相同，如果优势度是0，代表构成各景观类型占据的比例是相等的，它的景观全是均质的，就是采用一种景观类型构成的。具体计算公式为

(4)

式中：D代表优势度指数，Pi代表景观种类i所占据的面积比例，i代表景观类型的总数，Hmax代表研究区域的多样性指数最大值，而均匀度与优势度在其本质上是相同的，其差异为生态学上的意义不相同，在实际上能够任选其一。

5)均匀度指数E，主要是描述景观内不同景观种类所分配的均匀程度，数值越大，则说明各组成的成分分配就越均匀。具有计算公式为

E=(H/Hmax)×100%

(5)

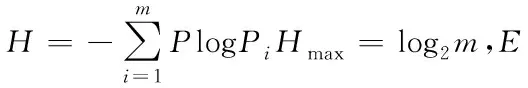
优势度与均匀度是相同的，同样是叙述景观通过极少数几个主要景观类控制程度，此两个指数能够互相彼此验证。

6)破碎度的指数表示被分割破碎程度，其在一定程度上能够反映出人为对于景观的干扰程度。利用斑块密度的指数对破碎化程度进行定量分析，而破碎度高低证明绿地对于城市生物的保护贡献大小以及多样性的维持，同样能够代表城市绿地的功能高低，具体公式公式为

Ci=Ni/A

(6)

式中：Ni代表景观种类i斑块的个数，A代表景观总面积。

7)分离度指数表示某景观种类内斑块个体分布或者不同元素的分离程度。其中分离程度越大，则说明在地域中的分布越分散，所采用的同类景观距离最近指标表示分离程度。具体计算公式为

ENN=Hij

(7)

式中：ENN代表景观种类i分离程度，Hij代表某种景观种类斑块至距离最近的斑块，该指标广泛应用于衡量斑块分离程度。

8)分维度的指数代表存在不规则形状的对象复杂性，主要用来测试形状复杂的程度。具体公式为

D=2log(P/4)/log(A)

(8)

在分维几何内，斑块的周长与面积关系可以被定义成P=K(AD/2)。

式中：D代表分形的维数，P代表斑块的周长，A代表斑块的面积，它的常数K等于4。实际计算内，D值通常位于1～2间，实际意义存在两个方面：一是D值越趋近于1，那么斑块自我的相似性就越强，形状就越具有规律；二是D值越趋近于2，那么斑块几何形状就越简单，说明受干扰程度就越大。造成这个原因的是，人类干扰的斑块通常是几何形状，比较规则。所以容易发生斑块的形状类似情况。若只从分维数自身的数学公式证明。其仅表示斑块自我类似性而已[7]。

9)连通性指数代表景观聚集程度，它的范围是0～100间，具体公式为

(9)

关键种类占据景观比例降低，且分成不连接的斑块，斑块结合度指数值趋近于0，在关键类型占据景观比例增加，一直至渐进于渗透理论阈值[8]。

2.2 景观可达性影响因素

1)城市景观可达性通常是指绿地服务效率和景观绿地服务进行体现，景观绿地服务的规模以及服务的半径等，现对于服务水平具有一定作用。具体景观绿地的服务指标含有服务面积比以及服务人口比，公式如下

(10)

(11)

2)景观的服务效率作为衡量城市景观绿地服务水平重要指标，主要通过服务面积百分比形式所体现，具体公式为

(12)

3)人口密度是作为衡量城市的公共服务重要指标，一般也用来评价景观绿地服务能力指标之一，而人口的密度是景观绿地服务的面积和服务区域总面积比，具体公式为

(13)

4)城市路网作为一个错综复杂网络构造体系，因人口流量、交通流速以及道路等级等实际情况差异。所以路网密度是指景观服务面积中道路的总长度和此服务区域的总面积比，具体计算公式为

(14)

5)景观绿地的形状指数作为空间构造重要指标，主要用来反映景观的形状特征，具体公式为

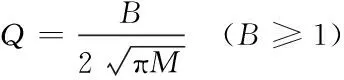
(15)

式中：Q代表景观绿地的周长，M代表景观绿地的面积，B代表形状指数，而数值代表景观绿地形状和圆形相差程度，最小值是1。其中形状的指数越大，代表绿地的形状复杂程度就越大，且越不规则[9]。

3 动态视觉景观规划

假设n″代表城市绿地景观图像像素最大至，p(i″，j″)代表景观图像的共生矩阵内第i″行第j″列元素，(i″，j″)代表共生矩阵的灰度值，通过选择4种应用比较广泛纹理特征叙述向量，以此对城市生态景观进行分析，而选择的叙述向量分别是角二阶矩ASM、相关系数COR、信息熵ENT以及对比度CON，具体计算公式为

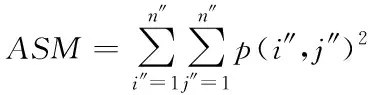
(16)

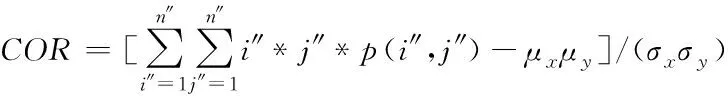
(17)

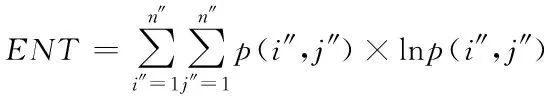
(18)

(19)

式中：μx、μy与σx、σy分别代表景观图像处于x轴与y轴上均值以及标准差，式(19)代表景观图像粗糙纹理的部分，若元素p(i″，j″)集中于主对角线的附近，这时景观图像的对比度CON比较小[10]。若元素p(i″，j″)与景观图像的主对角线比较远，那么对比度CON值则比较大；式(18)可以度量景观图像的纹理特征向量；式(17)能够衡量景观灰度共生矩阵的每个元素间类似程度重要指标；式(16)主要是用来评价景观灰度分布程度度量的标准[11]。

相对于景观系统图像的各个方向灰度矩阵全都能够计算上述，获得4个纹理特征值，而景观图像四个方向灰度的共生矩，各个纹理特征全有和值所对应的四个不同方向值，如果M(d)代表以上所计计算的4个纹理特征叙述向量处于4个方向上均值，那么就能够获得城市景观系统的角二阶矩、相关系数、信息熵以及对比度。具体计算公式如下所示

(20)

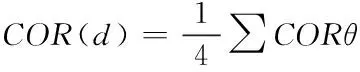
(21)

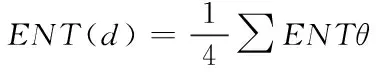
(22)

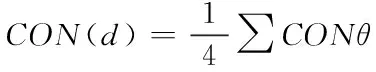
(23)

依据以上计算统计城市系统各种景观4个纹理特征值间的差异状况，并且与上述的空间格局指标相结合，利用最大似然法实现分类，完成景观布布局规划，具体计算公式为

(24)

式中：We代表景观类别集合，X代表景观纹理特征的叙述向量，P(We/X)代表X掉落在We概率，在依据式(24)概率值大小，即可实现景观布局的最佳规划[12]。

4 仿真证明

4.1 实验模型

为验证本文方法的有效性，在MAT-LAB平台下构建景观布局规划模型，进行实验仿真测试。将实际数据与实验平台上构建的模型数据进行对比，观察构建的模型是否准确，作为后续进一步实验测试的基础。

具体模型数据与实际数据之间的对比结果，如图1所示，能够看出，构建的模型数据与实际数据几乎相同，虽然会存在些许的偏差，不过总体上并不会影响数据的实际结果，以此说明在平台上构建的模型，可以用来进行下一步实验。

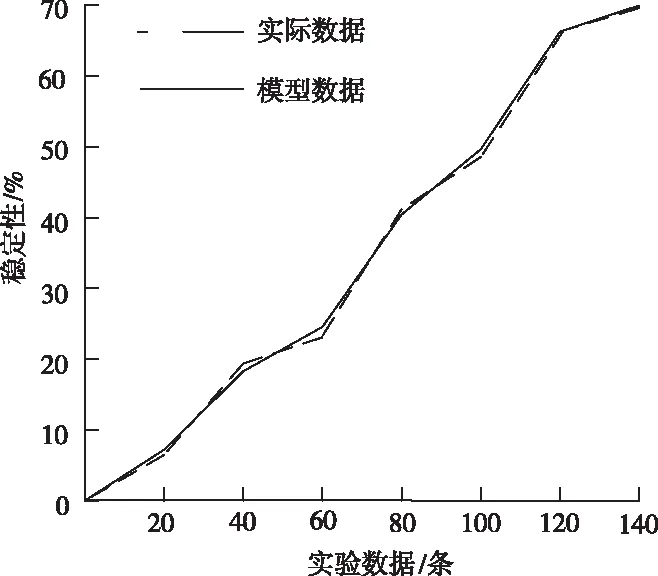
图1 实验数据对比结果

4.2 实验结果对比分析

利用上述在平台上构建的模型，分析本文的布局规划方法，同时预测未来6年内的景观植被面积，将预测结果数据与历史数据进行对比，通过观察植被的规划面积验证本文方法的效果。

二者具体对比结果如图2所示。

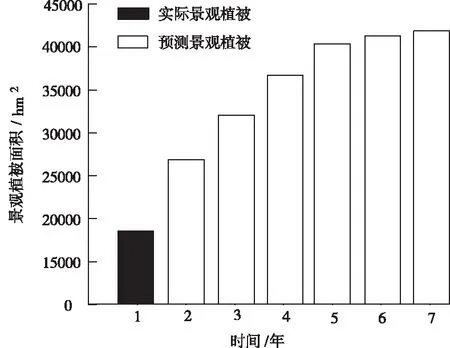
图2 景观绿地植被的面积预测

通过观察图2能够看出，经过本文方法规划后的景观植被面积，呈现逐年上涨的趋势，不过由于植被的面积与城市人类活动的面积存在反比的关系，植被数据的增加，反之人类活动的面积则减少，所以植被虽然逐年增加，不过后期增加的趋势会较慢。

因为植被的增加，会导致空气中的二氧化碳含量降低，因此通过测试二氧化碳的含量，能够反映出空气环境的变化效果。所以在采用本文方法规划后空气中的二氧化碳含量，与历史数据对比，观察环境的改变。

具体对比结果如图3所示。

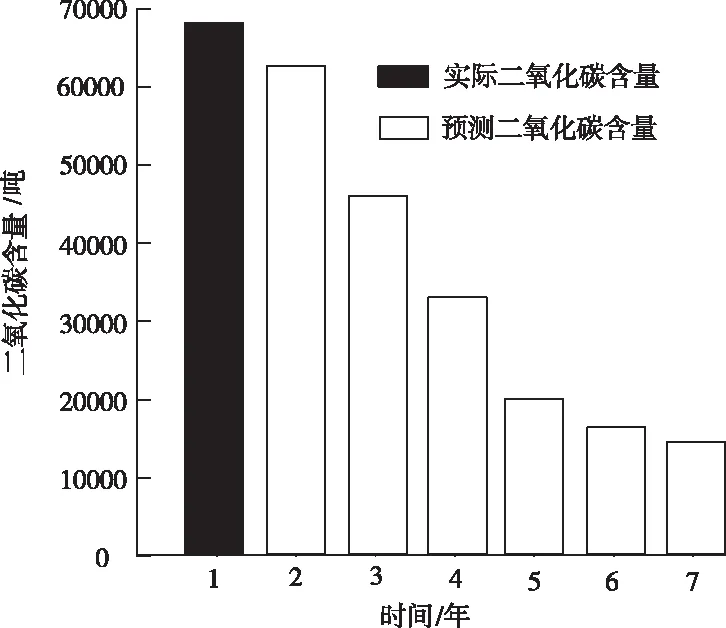
图3 二氧化碳的含量预测

通过图3能够看出，作为实际样本数据二氧化碳的含量较高，不过随着本文方法对景观进行规划后，植被的面积增加，二氧化碳的含量随之在逐年的降低，最终趋向于稳定。

通过以上实验证明：本文方法对于景观规划具有良好的效果，能够改善地区生态环境，降低空气污染。

5 结束语

本文所提的基于数据量化分析的动态视觉景观规划仿真方法，可以有效改善景观环境，降低空气污染，提升居民的居住环境，保证健康。不过由于社会环境不断变化，同样布局规划的方法也需要不断更新变化，所以本文需要进一步深入研究，确保可以实时与社会环境相结合，避免环境受到污染。