基于GAM的感应电动机比例预测方法研究

张湘驰，田 玲，高建良，向 行

(1. 中南大学计算机学院，湖南 长沙410083；2. 国网湖南省电力有限公司信息通信分公司，湖南 长沙410004)

1 引言

随着科学和经济的快速发展，电力需求日益增长和电力系统的规模不断扩大，电网运行条件日益复杂，其中，电压稳定性问题引起了日益广泛的关注和重视[1]。感应电动机动态负荷在电力负荷中占比高达60%～70%，特别在工业负荷中占比90%以上，对电力系统运行分析与控制具有相当大的影响[2，3]。因此感应电动机比例在维护电网稳定性和保证电力系统运行的安全性以及可靠性的任务中起到至关重要的作用。

目前，在华中电网负荷采用一定比例的感应电动机与恒定阻抗的并联作为暂态稳定计算的综合负荷模型[4]。文献[5]利用统计综合的方法基于用户终端采集到的有功功率进行按不同行业分类进行加权求和平均后估计，得出了某电网感应电动机和恒定阻抗的比例。但统计综合法负荷建模计算感应电动机比例虽然具有思路清晰、便于理解等优点，但由于此方法需要统计大量客户侧负荷的数量及运行状态。因此，华中地区基本上沿用多年以来指定的感应电动机比例参数固定值(例如某地区采用的是65%的感应电动机比例[4])。文献[6]基于智能电表的实时数据采集以及通信的快速传输，实现了变电站供电区所属全部用户有功的自动采集，在线计算变电站负荷模型中感应电动机比例。感应电动机比例的确定对于仿真结果存在误差影响，误差的大小及性质对电网决策的正确性具有决定作用，如果为了防止事故的发生采用保守的感应电动机比例参数，则会因为投入过多的资金和设备造成资源的浪费；如果为了防止资源的浪费采用激进的感应电动机比例参数，则会因为反事故措施方面投入资金和设备不足导致电力系统在运行时造成危险事故的发生。

基于感应电动机比例对于电力系统正常运行的重要性和意义以及存在问题仍未解决的情况，提出了TP-GAM(Trend and Periodicity Generalized Additive Model)方法，基于历史数据的特征挖掘和数据分析进行未来一段时间的感应电动机比例预测和发展趋势预测。主要的技术手段是采用时序数据分析预测，基于电力系统中感应电动机比例的时序性，从历史数据的分时段以及分行业的分布情况中挖掘数据特征，为电网决策设定感应电动机比例取值提供参考对比，提高电力调度处理的效率。

2 TP-GAM方法研究分析与设计

本文提出的针对感应电动机比例预测的TP-GAM方法研究。针对电力时序数据特点设计，综合考虑了数据的缺失情况、电力时序数据的趋势性、周期性以及长期历史数据的惯性[7]。TP-GAM分为3个部分，分别为纵横结合异常检测、感应电动机比例的逐级聚合计算以及感应电动机比例预测。

2.1 纵横结合异常检测

由于电网数据采集的不可重复性，在冗余量不足的情况下，使用缺失电能质量数据进行分析得出的结论与正确的规律有较大的偏差[8]。因此本文提出纵横结合异常检测对缺失有功功率数据进行填充修正来保证数据的完整性。

本文设定历史数据的日期窗口大小Th，采用日期窗口内的历史日期同一时刻的数据进行日间数据移动平均的方法进行缺失值，这可以拟合当前缺失数据与历史数据在部分时刻的波动趋势，具体公式为

(1)

其中val(f)为填充值，val(h)为当前日期的前h天同一时刻历史数据。

针对缺失填补后的数据以及原有的未缺失数据进行异常检测，采用短期环比横向异常检测与同比振幅纵向异常检测的纵横结合的方式以判定异常点。

2.1.1 短期环比横向异常检测

对于有功功率时序数据，T时刻的数值对于T-1时刻有很强的依赖性，利用横向的短期环比异常检测方法获取最近时间窗口(T)内的数据遵循的周期特征。将T设置为n，取检测值(valf)即上一步填充值和过去n个时刻进行比较，如果大于阈值将count加1，如果count超过设置的nums，则认为该点是异常点，公式如下

(2)

td=min(max-avg，avg-min)

(3)

其中，H为短期环比横向异常检测结果；vali为时刻i的数据；动态阈值td是针对T时间窗口内时序数据进行计算，T时间窗口内数据的最大值为max，最小值为min，平均值为avg。

2.1.2 同比振幅纵向异常检测

时序数据中每一个值不仅需要满足同一天内时刻变化的序列横向周期性特征，也需要满足连续d天内同一时刻遵循的纵向周期性特征。因此本文采用同比振幅纵向异常检测方法查找有功功率时序数据中的离群点。

(4)

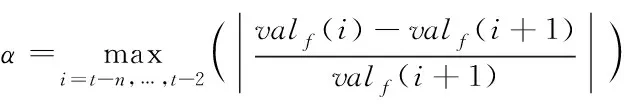
(5)

ts=min(MAX-AVG，AVG-MIN)

(6)

其中，V为同比振幅纵向异常检测结果；valf第f时刻的数据即待检测值，valf(t-1)为第t-1天时刻f的数据；静态阈值ts是针对全天时序数据进行计算的，全天数据的最大值为MAX，最小值为MIN，平均值为AVG。

对于异常检测方法检测出填充值为日内时序数据的离群点异常的情况，需要参考实际变化情况和时序数据变化趋势采取修正的方法使其符合日内波动。

2.2 感应电动机比例逐级聚合计算

将缺失的有功功率补充完整后，考虑到不同行业产生的负荷大小不一样，不同地区因为地理位置、人口密度以及行业分布等因素都会导致感应电动机比例的变化。因此本文分变电站级别、城市级别、省份级别将不同行业的有功功率进行加权求和平均化，逐级聚合计算得出感应电动机比例[9]。

首先是按照不同行业用电聚合到变电站计算感应电动机比例。公式如下

(7)

其中，kms为变电站的感应电动机比例；n为该变电站下有n种行业用电；kn为对应行业的权重；Pn为对应行业的有功功率。

其次，从不同变电站用电聚合到各地市计算感应电动机比例。公式如下

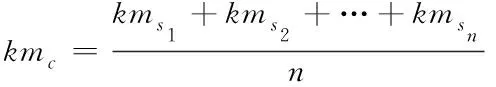
(8)

其中，kmc为地级市的感应电动机比例；n为该地级市下有n个变电站。

最后，从不同地级市用电聚合到省级别计算感应电动机比例。公式如下

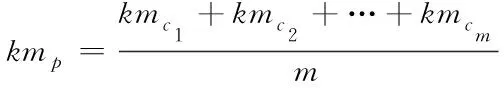
(9)

其中，kmp为省份的感应电动机比例；m为该省份下地级市的数量。

2.3 感应电动机比例预测

本文基于广义可加的非线性回归模型来预测感应电动机比例，主要通过拟合感应电动机比例中的趋势项的逻辑回归增长g(t)、周期项的傅里叶级数周期性s(t)以及无法预测的因素的误差项εt组成，公式如下

y(t)=g(t)+s(t)+εt

(10)

其中，y(t)来表示感应电动机比例预测值。

2.3.1 趋势性

在某些如季节更替月份的变点，感应电动机比例的每一段数据的趋势会随变点的情况而改变。为了挖掘时序中蕴含的非线性增长的趋势变化，因此采用分段的逻辑回归增长算法。用g(t)表示趋势性变化，其具体形式如下

(11)

(12)

其中，C(t)为曲线饱和值；k+a(t)T为曲线增长率；δ=δj表示在时间tj处的变化量；m+a(t)T为曲线中点；γ为sj处的平滑处理偏移量，sj为第j个变点的时刻。

2.3.2 周期性

大部分的时序数据都具有天、周、月、年等周期性的变化。所有的周期性函数都可以通过正余弦函数叠加来表示，因此采用傅里叶级数来构造灵活的周期性模型。用s(t)表示周期性变化，其具体形式如下

(13)

其中，P为周期，an，bn为平滑参数，N为傅里叶阶数。

3 实验

本文以某地区220kV真实的感应电动机比例数据进行实验，并且将本文提出的与ARMA模型[10]进行对比，结果表明TP-GAM具有更高的精确度以及稳定性。

3.1 电力感应电动机比例数据分析

本文实验采取的数据集为某地区某年6月至11月时段的220kV感应电动机比例数据。为挖掘感应电动机比例的趋势性变化、日间以及日内的波动规律，本文对原始的感应电动机比例数据进行分析。如图1所示，本文选取其中一周的数据。从每天的曲线观察到日内波动分明，与居民工作和生活息息相关。在早晚高峰时间段，有明显上升或下降的波峰和波谷出现。同时周内波动也十分明显，工作日相对休息日感应电动机比例呈现增长趋势。休息日呈现下降趋势，从周六开始，当天的整体感应电动机比例曲线相比较于周五有了显著的下降。到了周日，这天的整体感应电动机比例曲线下降趋势更显著。然后从周一开始，每天的整体感应电动机比例逐步上升。这是因为双休日时期，大部分企业工厂休息，感应电动机比例会明显降低；等到新的一周的开始，企业工厂开始上班，感应电动机比例因此重新上升。

图1 连续7天感应电动机比例变化曲线

3.2 实验评价指标

本文选取平均百分比误差(MAPE)，平均误差(ME)以及均方误差(MSE)三项评价指标作为与ARMA模型的评价指标[11]，公式如下所示：

(14)

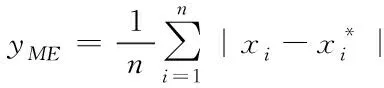
(15)

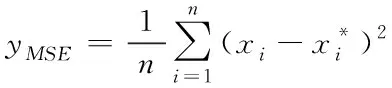
(16)

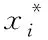
3.3 结果分析

3.3.1 缺失数据处理对比

用某地区220kV某变电站有功功率(MW)时序数据，随机去掉部分时间点的值，检测到0值进行填充示例结果如表1。对于绝大部分缺失数据，填充结果与真实值之间浮动比均小于10%，表明填充效果好。同时通过短期环比横向和同比振幅纵向两种方法来检测填充异常，然后进行修正示例结果如表2所示。对于少量填充异常点进行检测修正后，修正值更接近真实值。其中，填充值浮动比由填充值减去真实值的绝对值除以真实值计算所得，修正值浮动比由修正值减去真实值的绝对值除以真实值计算所得，优化量由修正值浮动比减去填充值浮动比求得。

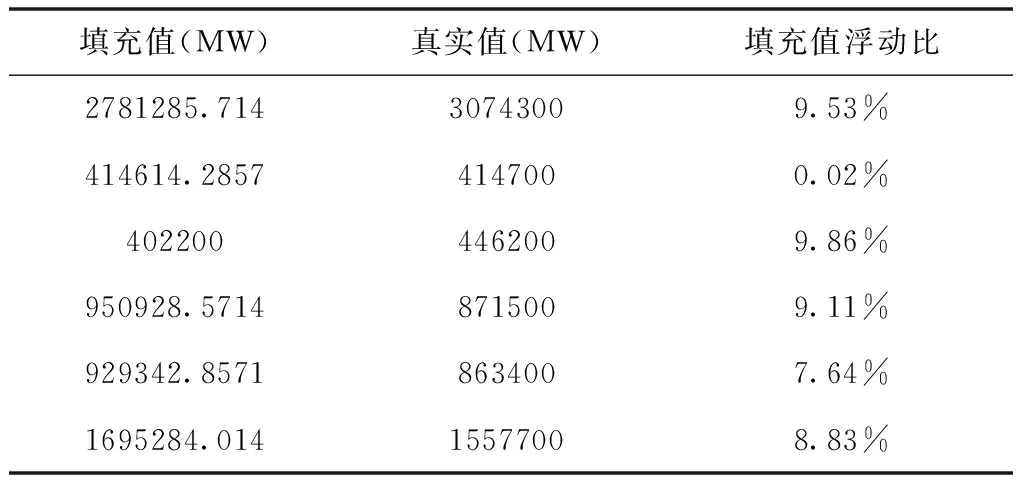
表1 缺失值填充示例

表2 填充异常修正示例

3.3.2 对比实验

将TP-GAM拟合完成后，本文利用某年6月1日到10月31日的感应电动机比例进行11月其中8天的短期预测。与ARMA模型预测的值进行对比，其对比结果如图2所示，TP-GAM预测的结果明显优于ARMA模型，实线为真实值，虚线为ARMA模型预测结果，预测与真实值差异较大；点横线为TP-GAM预测结果，预测与真实值更为接近。

图2 预测结果对比

表3 对比方法的预测精度比较

本文采用了MAPE、ME以及MSE作为评价指标，对比与ARMA模型的预测10月和11月感应电动机比例的精度。其结果如表3所示，TP-GAM在3个指标上均表现效果最好。尤其是在MSE方面分别比ARMA模型小3倍和4倍。同时，3个评价指标在改变历史数据跨度时，TP-GAM效果波动小且更稳定。

4 总结

由于感应电动机动态负荷在电力负荷中占比很高，为维护电网稳定性和保证电力系统运行的安全性，本文设计了一个针对感应电动机比例预测的TP-GAM框架。首先通过利用短期环比横向和同比振幅纵向相结合的异常检测方法对时序数据的缺失情况进行检测和填充修正；其次根据变电站、城市、省份三个级别进行逐级聚合计算感应电动机比例；最后利用广义可加的非线性回归模型对感应电动机比例的时序历史数据进行周期性和趋势性的特征分析和预测。本文以某地区真实的负荷时序数据做算例验证，结果表明这是一个既满足精度需求又能提高经济效益的感应电动机比例预测方法，为电网资源的合理分配和电力系统运行以及规划提供数据支撑有较大的现实意义。