基于弃风惩罚的电力负荷经济调度研究

2023-03-29陈盈君徐浩东

计算机仿真 2023年2期

徐武，陈盈君，文聪*，徐浩东

(1. 云南民族大学电气信息工程学院，云南昆明 650500；2. 陕西长庆专用车制造有限公司，陕西咸阳 712000)

1 引言

近年来，由于环境污染问题日益严重，以风电为代表的新能源电场明显增加，但是弃风现象严重，而且风能发电具有间歇性和反调峰性，损害了经济利益，降低弃风和风火互补成为了研究热点[1]。

针对以上问题，文献[2]利用储能系统对风力发电进行削峰填谷，提高了风电接纳量，并具有良好的经济性，但建立储能系统成本太高[2]。文献[3]利用极限穿透功率的风电场弃风惩罚模型，虽然能衡量损失但其模型忽视了对风电预测精度评估[3]。文献[4]针对火电厂负荷指令利用改进混沌粒子群算法做最优负荷分配实现了经济效益最大化，但是没考虑新能源发电，环境成本较高[4]。文献[5]建立了考虑火力发电成本、风力发电成本和弃风惩罚成本的模型，并用改进萤火虫算法对模型求解，但其弃风惩罚模型没考虑分段弃风惩罚成本，无法达到减少弃风，抑制反调峰现象的目的[5]。文献[6]构建了包含风险惩罚、电网安全约束和机组特性的风电并网模型，此方案强调了风电并网的风险评估，提升了风火互补发电厂的稳定性，但是缺少经济性方面的研究[6]。基于此，本文提出了一种基于风力发电便捷性评估的综合弃风惩罚模型。首先通过风电场的出力稳定性和对其出力的预测准确性来评估便捷性，得到权重系数，结合分段弃风惩罚成本系数抑制风电场的弃风现象和反调峰性；然后建立了一个以经济性为目的的风火互补优化发电模型，利用火电厂弥补风力的间歇性和不稳定性；利用改进BQPSO增强全局搜索能力和最优粒子权重，并对虚拟电厂进行负荷分配。

通过仿真分析，证明了提出的弃风惩罚模型可以有效减少弃风现象，抑制风电场的反调峰现象，增加优质风能的利用率，改进的BQPSO算法既能利用火电弥补风电的不稳定性，又能使火电厂煤耗量降低，获得更多经济效益。

2 弃风惩罚模型

风能资源具有储量丰富，成本较低，不会对环境造成污染等优点，但是由于风电的间歇性和不可预测性，导致风电场弃风现象日益严重[7]。目前弃风惩罚模型一般如式(1)所示

(1)

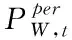
这种算法认为所有风电场的弃风成本相同，忽略了不同风电站成本差距，不能达到将弃风成本降到最低的目的[8]。针对以上问题，本文考虑到风电场权重和分段弃风惩罚成本，提出一种综合弃风惩罚模型，如图1所示。

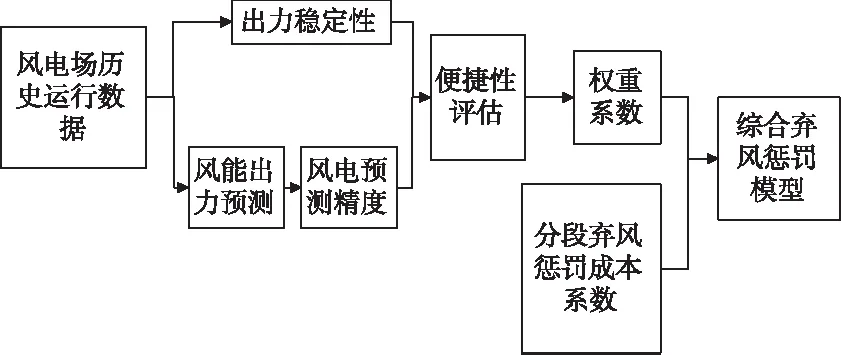
图1 综合弃风惩罚模型

通过评估风电场出力稳定性和预测精度，保证选择的风电场权重系数大。随着弃风量增大，分段弃风惩罚系数增大，从而起到抑制弃风的效果。

2.1 风电惩罚权重系数设定

确定对不同的风电场的弃风惩罚权重系数需要考虑风能出力稳定性和风电预测精度两个因素，对于出力稳定性好，预测精度高的风电场给予较高权重[9]。

风电场出力越稳定，对电网的影响越小，以平均出力波动率fv作为稳定指标

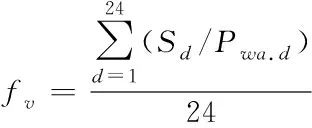
(2)

其中：Sd为在第d小时中，10分钟内的功率标准差；Pwa.d为在第d小时里求得的平均功率。

一般结合预测的风电场出力和调度中心的目标负荷来决定火电厂的备用容量，风电预测准确度越高，风电利用率越高。平均精度ηv为

(3)

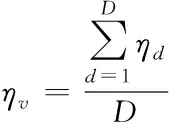
(4)

其中，ηd为第d小时预测精度；Pwp.t为风电场在时段t的预测出力；Pwf.t为实际出力；T为第d小时调度总时段数；Pw为风电场总容量。

综合考虑上面提出的出力稳定性以及出力预测精度指标，得到此风电场的便捷因子λ，并将其作为权重系数的参考[10]。权重系数越大，此风电场越容易被调用。在选择弃风对象时，优先选择权重小的风电场。风电便捷因子λ为

(5)

其中：fv.i为机组i的平均出力波动率、ηv.i为平均风电预测精度；NW为总机组数。

2.2 分段弃风惩罚成本设定

通过分段设置，随着弃风量的增加，弃风成本也随着增加，起到降低弃风的目的，根据不同的地区，季节，早晚确定相应的分段值，分段弃风惩罚成本为

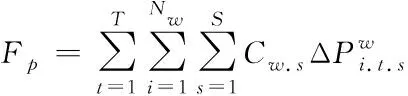
(6)

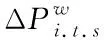
2.3 综合弃风惩罚模型

在分段弃风惩罚成本中考虑风电便捷因子λ得到综合弃风惩罚模型

(7)

该模型能考虑风电机组的出力便捷性以及分段弃风惩罚成本。

3 风火互补优化发电模型

以系统最低能耗为目标，优先接收弃风惩罚成本低的原则，建立风火互补优化发电模型。

3.1 目标函数

为了将发电成本降到最低，系统优化发电目标函数为风电机组和火力机组总成本最低[11]。优化目标为

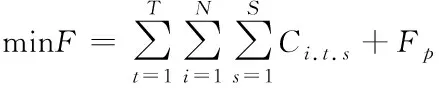
(8)

其中：N为火电机组数；Ci，t，s为火电机组i在时段t第s分段的发电成本。

3.2 约束条件

风电并网和限风后，经济性作为最优目标进行优化分配，而且需要让系统总负荷等于电网负荷指令，系统功率平衡约束条件为

∑P+∑Pwf=∑P1+∑Pd

(9)

其中，P为火电厂输出功率；Pwf为风电场输出功率；P1为调度中心下达的目标负荷；Pd为系统损耗功率。

在考虑风电并网时，由于风电机组安全运行的需要，要考虑风电机组的出力上限约束

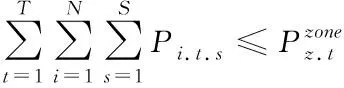
(10)

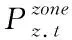
将火力发电作为发电场的备用容量，来调节风能的出力不稳定，约束条件为：

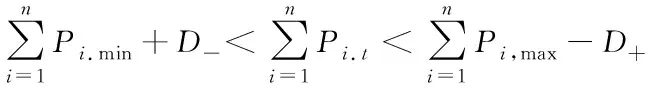
(11)

4 二进制量子粒子群算法及改进

由于本文采用的弃风惩罚模型以及火力发电弥补风能发电模型需要求解最优方案，粒子群优化算法可以满足要求。但是，粒子群算法容易陷入局部最优，所以引入改进BQPSO算法[12]。

4.1 二进制量子粒子群算法

在PSO算法基础上，提出具有量子运动特征的粒子群算法(QPSO)，粒子位置更新不受之前位置的影响，因此搜索空间也不受限制，能收敛到全局最优解[13]。BQPSO是在QPSO基础上将粒子位置由二进制表示，优化了QPSO在离散空间中求解的效果。式(12)表示在QPSO算法中仅用一个位置更新公式来表示粒子的位置和速度：

zi(t+1)=Pi(t)±β·Li(t)·ln[1/ui(t)]

(12)

其中：Pi(t)称为吸引子；β一般小于1；t是当前迭代次数；Li(t)表示zi(t)与mbest距离的绝对值。

在第n次迭代时，算法迭代公式为

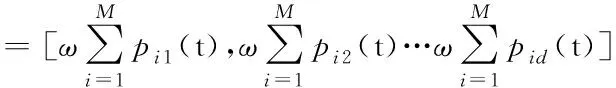
(13)

pi=φ×pbesti+(1-φ)×gbest

(14)

其中：mbest为平均最优位置；Pi为粒子位置更新公式；φ是(0，1)上均匀分布数值；gbest为当前全局最优值。

BQPSO是在QPSO的基础上将粒子位置由二进制数表示，式(15)表示两个粒子位置的距离

|X-Y|=dH(X，Y)

(15)

4.2 算法改进

为了增强算法的全局性能，防止迭代后期粒子多样性减弱，陷入局部最优，从而造成负荷分配最终经济性方案不是全局最优解，本文增加了“粒子偏离度”检测公式，以及自适应干扰系数来避免算法局部收敛。由于在mbest的计算公式中不同粒子的权重相同，不能突出最优粒子的优先权，为了增加算法的收敛速度，本文改进了加权更新mbest(t)的计算公式。“粒子偏离度”检测公式如下

(16)

其中，fi为粒子i适应度，favg为种群平均适应度。当Δ逐渐降低，聚集程度增加。当Δ小于设定，认为局部收敛。

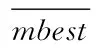
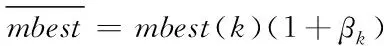
(17)

βk=c1[Ck(0，1)+c2Nk(0，1)]

(18)

(19)

其中βk为干扰系数。

同时，改进了mbest(t)的公式中的权重系数，将式(13)中ω改为权重系数ωi

(20)

式中f(Pi(t))为最优适应度。mbest的更新公式如下

(21)

可以看出，改进BQPSO算法首先在进入局部最优时，进行扰动算子干预，增加算法的全局性能；在计算BQPSO的mbest时，通过提高最优粒子在种群中的权重，也提高了算法的全局性能，而且使收敛速度提高。

4.3 算法步骤

初始化粒子数为50，设置仿真的结束条件为迭代2000次，将改进BQPSO算法求解负荷分配步骤简述如下：

步骤1：确定经济性目标函数wC和快速性目标函数wT所占比重；

步骤2：初始化粒子位置和初始种群数，并用二进制表示群体中的每个粒子的初始位置[14]；

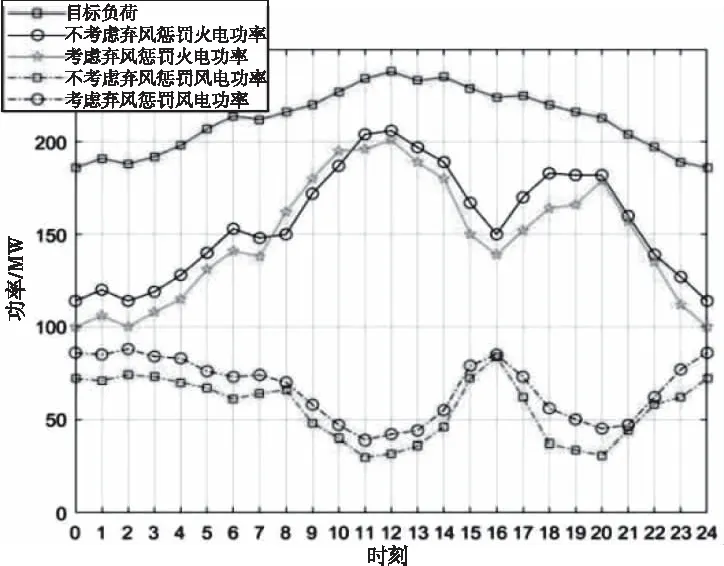
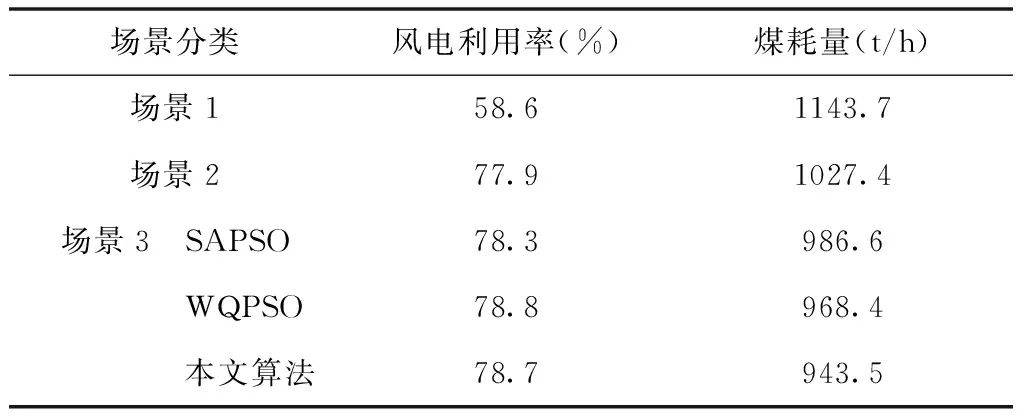
步骤3：计算适应度值，当f(xi(t))

步骤4：更新种群中的粒子位置；

步骤5：记录各粒子的个体极值pbest和全局极值gbest，本文求解模型的目标函数为在满足调度速度要求的前提下尽可能的获得经济效益，对于不满足约束条件的粒子，直接取其适应度为0[15]；

步骤6：根据公式计算mbest，得全局最优粒子Pg(t)；

步骤7：按照式(16)计算粒子偏离度，若Δ小于设定值，转到下一步，否则转到步骤9；

步骤9：对PPi进行变异，重新生成粒子群；

步骤10：当更新次数达到设定值，转到下一步，否则转到步骤3；

步骤11：将全局极值作为算法最优解，计算得到最佳的优化结果。

利用改进的BQPSO算法求解本文负荷分配模型流程如图2所示。

图2 算法流程

5 仿真分析

为了验证本文提出的弃风而惩罚模型的效果，以IEEE30节点进行仿真分析，设定第16节点和20节点为额定功率为50MW的风电机组。两台风电机组的数据如表1。表1中，机组平均出力波动率反应每小时出力功率的方差，平均预测精度反应了根据历史数据预测功率和实际功率相差程度。由表1可知，机组2的平均出力波动较大，而且平均出力预测精度较低，综合可知，机组2的并网便捷性较低。根据评估的风电机组并网便捷性可计算出2台风电机组的权重系数。

表1 风电机组权重系数

为了验证本文提出的弃风惩罚模型的有效性，选取某天24小时的调度时段，对于调度中心对电场要求的目标负荷，利用本文提出的BQPSO算法进行仿真分析。将仿真对象分为以下3种场景：1、不考虑弃风惩罚；2、不计算权重系数；3、计算综合弃风惩罚模型。对比如图3所示。

图3 场景1场景2中机组负荷

由图3可知，由于场景1不考虑弃风惩罚，所以风能利用率低，而且在8点到12点之间和16点到21点之间风电机组出现了反调峰现象，即调度中心要求的目标负荷较高，但风能出力下降。场景2相较于场景1计算了分段惩罚成本，即弃风成本随着弃风量增加而增加。

场景2和场景3中风电场整天实际出力和弃风率如表2所示。

表2 场景2和场景3弃风率对比

由表2可知，由于场景2未考虑权重系数，因此2台风电机组权重一样，弃风率大致相同；场景3考虑权重系数后，因为风电机组1的并网便捷性较高，所以权重系数较大，弃风率显著降低，而风电机组2的弃风率略有上升，可以反映出权重系数对于机组弃风率的影响较大。所以在考虑弃风时，并网便捷性低的风电机组2率先弃风，而在考虑风能调度时，优先调度并网便捷性高的风电机组1。

利用本文改进BQPSO算法对3种场景下24个时段中风电利用率和火力机组发电平均煤耗量以及用SAPSO算法，WQPSO算法和本文算法对场景3仿真对比见表3所示。

表3 3种场景弃风率对比

由表3可知，场景2计算了分段弃风惩罚系数，相较于场景1可以在降低火电厂煤耗量的同时大幅提升风电利用率；在场景3中综合计算了权重系数和分段弃风惩罚系数后，风电利用率有略微上升，而且煤耗量显著降低；而SAPSO和WQPSO算法相较于本文算法的风电利用率没有太大变化，但是用本文算法求解的煤耗量远低于其它两种算法，说明本文算法在计算火电厂的经济调度时更容易收敛于全局最优。因此，本文提出的弃风惩罚模型以优化风能利用率为目的，提高电力系统运行的经济性，降低风电场的运营难度。