基于AGA-Smith预估补偿PID的脱硝系统控制

孟宏君，王尚尚，张凯奇，李丽锋

(1. 山西大学自动化与软件学院，山西 太原 030013； 2. 山西大学数学科学学院，山西 太原 030006；3. 山西河坡发电有限责任公司，山西 阳泉 045011)

1 引言

煤炭粗放的利用方式及火电机组装机容量不断增加使得火电厂机组产生一系列大气污染物。山西省于2018年7月已将NOx浓度排放上限值调整为50mg/m3。循环流化床锅炉(CFB)因其NOx生成率低、循环物料、分级清洁燃烧等优势脱颖而出，受到我国火电厂的广泛青睐。

针对电站脱硝控制系统，国内外已有大量学者进行研究。文献[1]研究发现分离器是SNCR脱硝反应的良好场所；文献[2]研究了使用氨或尿素作为脱硝反应的还原剂，脱硝效果明显；文献[4]研究了NOx脱除率随温度的变化关系；文献[5]基于实际的运行数据和最小二乘支持向量机算法，采用复相关系数的时滞估计方法在一定程度上提高脱硝系统的NOx排放软测量精度；文献[6]研究表明将还原剂喷射点安置在分离器入口位置，脱硝效果明显；文献[7]研究了氧化钙对NOx浓度的影响；文献[8]研究了不同的喷氨方式对脱硝效率的影响；文献[9]将搭建的SNCR脱硝系统神经网络模型应用到现场，实现了在线预测NOx浓度；文献[10]采用主导变量分析法确定模型参数，预测反应器入口NOx浓度；文献[11]研究了影响NOx生成量的因素，通过自回归移动平均模型完成NOx浓度的预测；文献[12]利用遗忘因子最小二乘法建立了从喷氨量到出口NOx浓度的传递函数模型；文献[13]采用渐进辨识法构建了SCR脱硝系统模型；文献[14]基于自然选择的差分进化法构建SCR脱硝系统模型；文献[15]利用时间差分动态建模法降低脱硝系统模型的阶次；文献[16]采用复相关系数法，建立了带有纯迟延时间的脱硝系统模型；文献[17]利用变量相关度和最小二乘支持向量机建立了SCR脱硝系统模型；文献[18]将专家模糊控制应用到现场脱硝系统中；文献[19]将模型预测控制应用到现场脱硝系统中；文献[20]建立了多负荷段下的脱硝系统模型，设计了对应的切换条件；文献[21]通过神经网络辨识出脱硝系统的模型，配合预测控制对喷氨量实现控制。

上述文献对影响NOx浓度和脱硝效率因素研究较多，构建脱硝系统模型及脱硝策略的研究应用较少，仍存在构建出的脱硝系统模型精度不高，改进的脱硝策略相比传统的控制策略，控制效果有改善但不明显的现状。基于此，本文综合分析了NOx生成机理及影响SNCR脱硝效率的因素，利用不同于传统PSO算法的IPSO算法对SNCR脱硝控制系统在典型工况下的模型参数进行辨识优化，从而提高模型精度。在电站现场已有的单回路PID控制策略上，提出一种AGA-Smith预估补偿控制策略，并对两种控制策略效果仿真对比，最后进行模型鲁棒性验证，为电站现场脱硝控制提供技术参考。

2 NOx生成机理及SNCR脱硝技术

2.1 NOx生成机理

NOx包括NO、N2O、NO2、NxOy等，对大气环境造成污染的主要指NO、NO2，其中电站燃烧产生的NO占90%以上。按照NOx生成机理不同，NOx可分为燃料型NOx、热力型NOx和快速型NOx。CFB机组产生的主要是燃料型NOx，与燃料品种有关，NOx生成量随温度变化曲线如图1所示。

图1 NOx生成量与温度

2.2 SNCR脱硝原理及脱硝效率因素分析

2.2.1 SNCR脱硝原理

SNCR脱硝的核心是NH3与NOx的一系列化学反应过程。还原剂可选择尿素CO(NH2)2或氨水NH3·H2O。利用CO(NH2)2脱除NOx的反应式为

(1)

与此同时伴随着副反应的发生：

(2)

2.2.2 SNCR脱硝效率影响因素

影响SNCR脱硝效率的主要因素有反应温度、反应时间、氨氮摩尔比、还原剂喷射区域等[22]。

1)反应温度

反应温度与SNCR脱硝效率的关系如图2所示，最佳的温度区间在850～1100℃。温度过高时，NH3发生氧化变为NO和NOx；温度过低时，反应时间变长。而旋风分离器内的温度介于800～900℃之间，恰好作为脱硝反应场所。

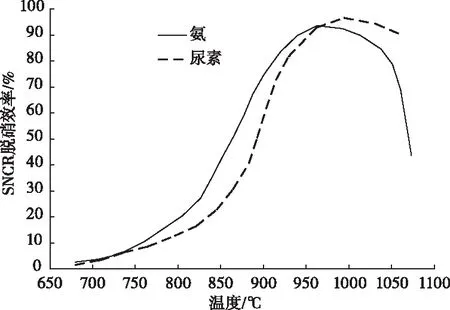
图2 SNCR脱硝效率与反应温度

2)反应时间

反应时间与SNCR脱硝效率的关系如图3所示，当还原剂参与反应时间>0.6s，脱硝效率较佳。

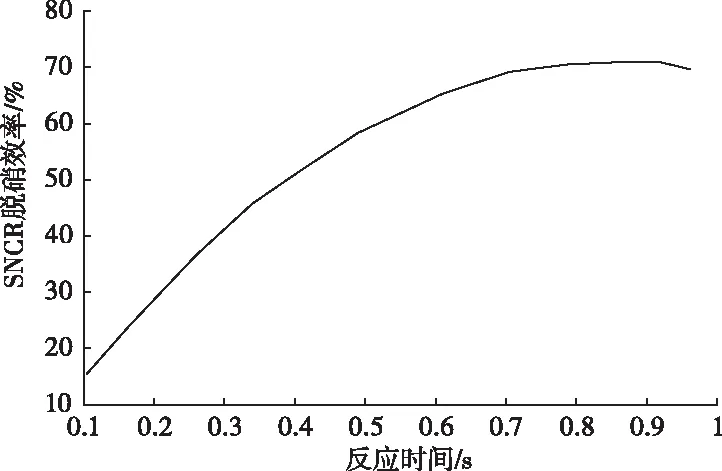
图3 SNCR脱硝效率与反应时间

3)氨氮摩尔比NSR

当还原剂为CO(NH2)2时，理论氨氮摩尔比NSR计算公式如式(3)所示

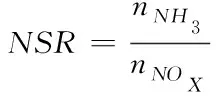
(3)

式中，nNH3为CO(NH2)2变换为NH3的摩尔数；nNOx为在未投入CO(NH2)2时，烟气中NOx浓度转换为标准状态、干基、6%氧气下NO2的摩尔数。

氨氮摩尔比NSR与SNCR脱硝效率的关系如图4所示，一般情况下，氨氮摩尔比取值大于理论氨氮摩尔比取值，取值在1～3之间。

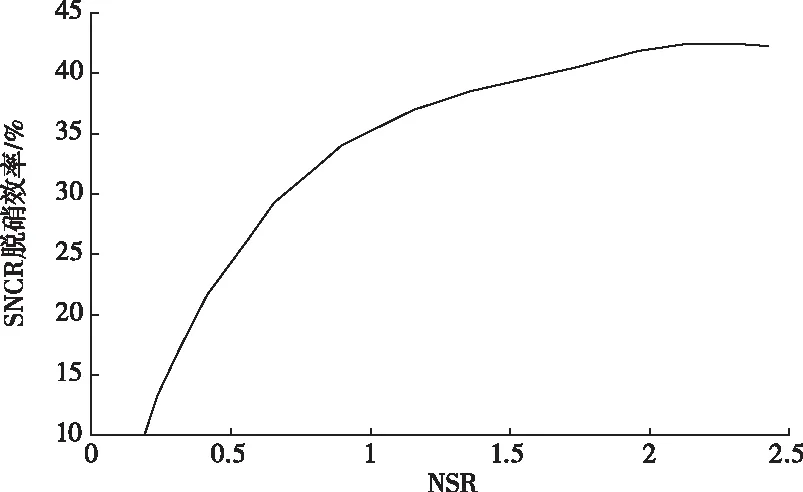
图4 SNCR脱硝效率与氨氮摩尔比

4)还原剂喷射区域

旋风分离器虽然可作为SNCR脱硝系统的反应场所，但还原剂的喷射区域也会对脱硝效率产生影响。研究表明，当喷射区域位于旋风分离器的入口位置，垂直均匀布置时脱硝效率最高。

2.3 试验机组介绍

试验机组为山西省某电站2×350MWCFB机组的1号机组，该电站配套有超临界变压直流运行的东方锅炉、一次再热双缸排汽的上海电气汽轮发电机、三台旋风分离器，燃烧的煤种为无烟煤。该电站SNCR脱硝系统的组成及作用如图5所示。

图5 SNCR脱硝系统的组成及作用

尿素与稀释系统、尿素溶液存储与输送系统都配套有搅拌器和加热装置，以防止由于环境温度过低造成尿素溶液出现结晶的现象。喷枪采用316L材质的墙式喷射器，分别布置在旋风分离器的入口烟道外侧三支、入口烟道顶端一支和出口烟道前墙一支，每台旋风分离器配置有五支喷枪，共15支喷枪，可根据锅炉负荷、燃料量的变化、NOx浓度等进行控制。

3 粒子群算法与遗传算法

3.1 粒子群算法

粒子群算法(Partical Swarm Optimization，PSO)最初于1995年由Eberhart和Kennedy二人联想鸟群觅食行为共同提出，是一种全局寻优的智能仿生优化算法。该算法的核心思想由m个粒子组成的群体，在N维搜寻空间用粒子的位置信息Xi、速度信息Vi和适应度值Qi，通过不断迭代更新，从而寻找到问题的最优解。基础粒子群算法的粒子位置和速度信息更新如式(4)、(5)、(6)所示

(4)

Vij(t+Δt)=Vij(t)+C1R1[Xbesti-Xij(t)]+

C2R2[Xbestgj-Xij(t)]

(5)

Xij(t+Δt)=Xij(t)+Vij(t+Δt)

(6)

式中，粒子最佳位置Xbesti，最佳适应度值Qbesti；群体最佳位置Xbestg，最佳适应度值Qbestg；i=1，2，3，…，m，j=1，2，…，N；当前时刻t，经过Δt时刻t+Δt；认知因子C1，社会因子C2；R1，R2∈[0，1]。

在基础粒子群算法粒子速度信息基础上引入惯性权重ω，即改进的粒子群算法，如式(7)所示

Vij(t+Δt)=ωVij(t)+C1R1[Xbesti-Xij(t)]

+C2R2[Xbestgj-Xij(t)]

(7)

ω的引入能够便于控制粒子群算法的收敛速度和寻优能力，常见的ω取值有线性递减权值法和收缩因子法两种，但这两种ω的取法存在一定问题，例如在算法初期收敛速度缓慢，算法后期容易陷入局部最优等。采用非线性递减权重法来弥补线性递减权值法和收缩因子法的不足，即在算法初期ω≈ωmax，全局寻优的能力较强，之后ω以非线性递减的方式减小，逐步缩小搜寻范围，局部寻优能力增强，ω表达式如式(8)所示，将这种PSO算法称为IPSO算法。

(8)

式中，最大惯性权值ωmax，最小惯性权值ωmin；当前迭代次数t，最大迭代次数tmax。

IPSO算法优化参数流程如图6所示。

图6 IPSO算法优化参数

从已知的模型结构出发，根据历史输入输出数据，利用IPSO算法进行模型参数辨识，模型辨识原理如图7所示。

图7 模型辨识原理

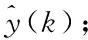
3.2 遗传算法

遗传算法(Genetic Algorithm，GA)最初于上世纪60年代由John holland受到达尔文生物进化论的启发提出，是一种基于“自然选择”和“基因遗传学原理”的并行随机全局优化自适应概率搜索算法。生物学概念与遗传算法的对应关系见表1。该算法的核心思想是编码、选择、遗传、变异和解码。遗传算法流程如图8所示。

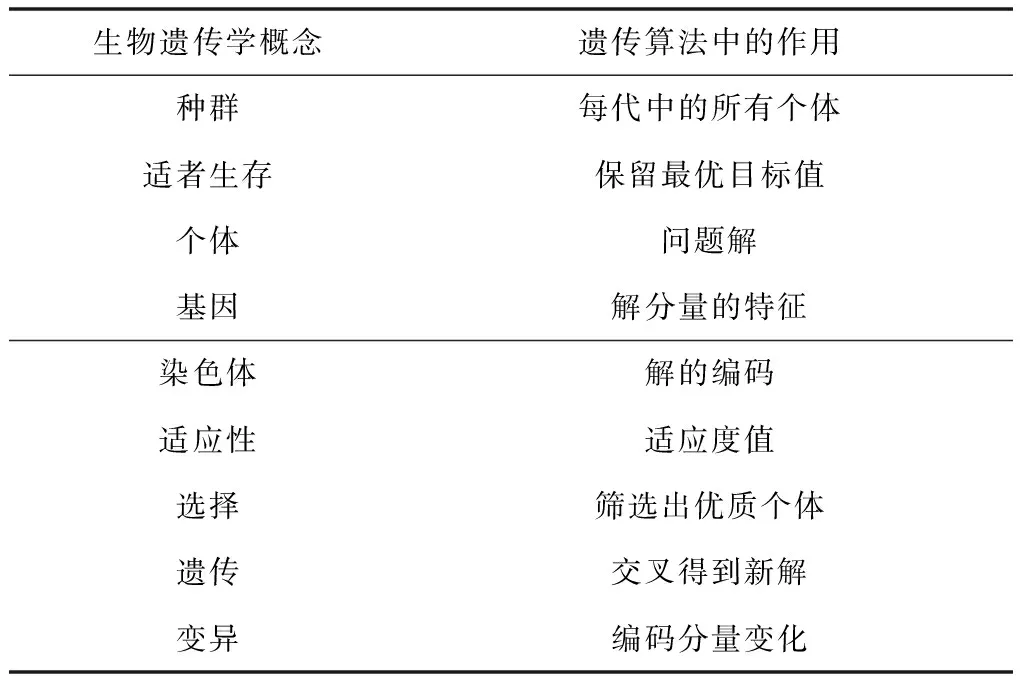
表1 生物遗传学概念与遗传算法

常见的编码方式有二进制编码、十进制编码、符号编码、实数编码等。选择方法有适应度比例法(轮盘赌法)、期望值法等；交叉方法有单点交叉、二点交叉、一致交叉等；变异方法有基本变异方式(某些特定基因座位置上的基因变为其等位基因，即1→0，0→1)、逆转变异、自适应变异等[23]。本文交叉概率与变异概率均设定为自适应变化概率，即自适应遗传算法(AGA algorithm)。

图8 遗传算法

4 数据采集与预处理

本文样本数据采集周期为6s，典型工况170MW和260MW下分别采集1800组样本值。工业现场环境的恶劣、电站系统结构的强耦合性与复杂性使得从DCS取出的数据或多或少夹杂着直流、高低频等不确定的随机成分，数据不能完全被使用，这些不确定因素最终都会对辨识的模型精度产生负面影响。因此为了保证采样的可靠性，减少不利因素，需要对DCS取出的数据进行预处理。

4.1 滤波处理

采用一次指数平滑滤波处理，如式(9)所示。指数平滑滤波本质上一种加权移动平均滤波器，剔除一些低频信息。

St+1=αxt+(1-α)St

(9)

式中，平滑系数α∈[0，1]，本文中α=0.005；t时刻数据的真实值xt；t时刻数据的预测值St；t+1时刻数据的预测值St+1。

4.2 归一化处理

由于从现场DCS采集回来的数据处于不同的量纲，量纲和单位不同影响数据分析的结果，为统一量纲，在同一数量级下进行数据指标的评价，进行数据归一化处理。

归一化的方法采用最大最小法，将所有数据变换到区间[0，1]之间，如式(10)所示

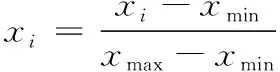
(10)

式中，xmin为数据中最小值；xmax为数据中最大值。

4.3 零初始值处理

传递函数模型是在零初始条件下定义的，当系统进入平衡态时，系统输入输出及各阶导均为零。现场DCS采集回的数据具有零点任意性，将热工过程实际零点与系统平衡点区分开[24]，因此要对采集的数据进行零初始值处理，如式(11)所示：

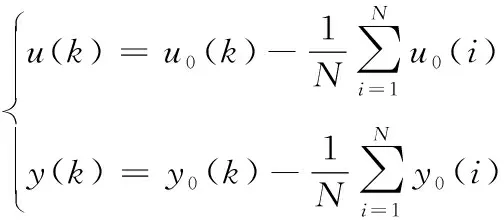
(11)

式中，N为零初始点数据的个数，本文中N=5。

5 控制策略及仿真分析

5.1 控制策略

热工过程被控对象的数学模型常用传递函数来表达，而传递函数只适用于线性定常系统，因此有必要进行线性化处理，设非线性函数y=f(x)，在其平衡点邻域内有y对x各阶导数存在，将y=f(x)在(x0，y0)处进行泰勒展开

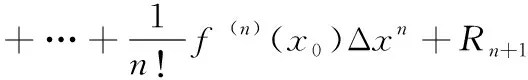
(12)

式中，Rn+1为余项。

忽略式(12)等式右端第二项后续项可得

y(x)=f(x0)+L′xΔx

(13)

式中，f′(x0)=tanα=L′x。

这样将非线性函数在平衡点邻域进行线性化处理，邻域范围越小，线性关系越强。

根据专家经验及前人文献分析，SNCR脱硝系统的模型可确定为带有纯滞后的多阶惯性线性环节，形式如式(14)所示

(14)

目前该电站的SNCR脱硝控制系统的尿素溶液流量调节回路受控设备为尿素溶液母管电动调节阀，尿素溶液流量控制采取单回路闭环控制和查表相结合的方式，在表中可查询不同负荷或烟气量对应的尿素溶液的喷射量，将表中查到的值作为单回路闭环控制的前馈值，同时烟气在线监测系统测量得到的NOx浓度反馈值对喷入的尿素溶液流量做出修正。

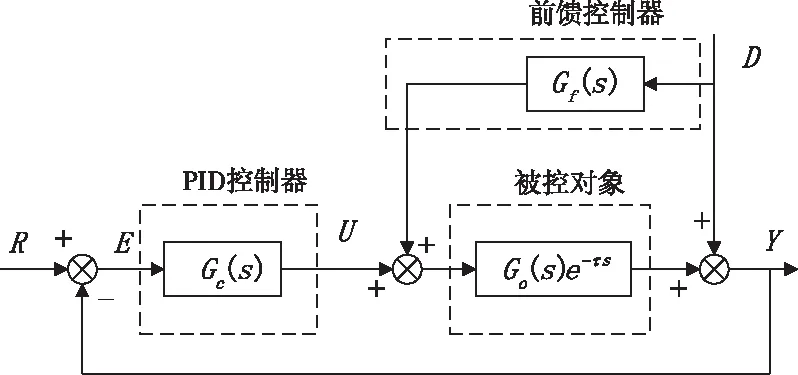
图9 单回路PID控制

现有的尿素流量调节控制策略没有考虑到被控对象的大迟延特性，控制效果易产生较大的超调，与此同时为了保证出口NOx浓度的实时达标，造成的直接后果是尿素溶液的喷射量过量，引起氨逃逸(氨逃逸是在标准状态，干基，6%氧气下出口烟气氨质量与烟气体积的比值，国家标准规定其比值应控制在8mg/m3以内)，逃逸的氨形成铵盐，吸附在锅炉尾部烟道，加剧设备的腐蚀，影响经济效益。

在此基础上，引入Smith预估补偿控制，克服大迟延带来的问题。Smith预估补偿控制的缺点是受到控制对象数学模型的限制，必须事先掌握精确的数学模型，控制器的参数依然按照经验进行调节。为此引入自适应遗传算法，对Kp、Ki、Kd三个参数进行优化，优化控制效果。

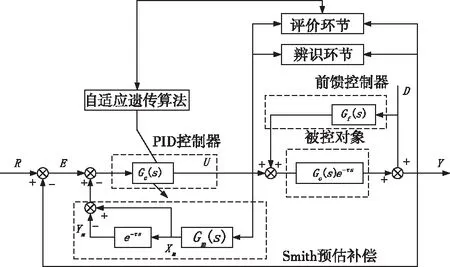
图10 AGA-Smith预估补偿控制

5.2 仿真分析

5.2.1 IPSO算法参数设置

参数范围：K∈[-5，5]；T∈[1，400]；n∈[1，4]；τ∈[0，150]

种群规模：D=100

迭代次数：N=200

速度区间：v∈[-1，1]

惯性权重区间：ω=[0.1,0.9]

学习因子：C1=C2=2.02

5.2.2 自适应遗传算法参数设置

参数范围：Kp∈[-8，8]；Ki∈[1，10]；Kd∈[0，100]

种群规模：D=50

迭代次数：N=100

染色体长度：L=20

编码方式：实数编码、线性插值

变异概率：Pm=0.2-[1：N]*0.04/N

变异操作：逆转法

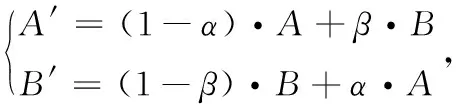
5.2.3 仿真结果

由IPSO算法辨识得到SNCR脱硝控制系统在170MW典型工况下的传递函数模型为：

图11 170MW下辨识效果

由IPSO算法辨识得到SNCR脱硝控制系统在260MW典型工况下的传递函数模型为：

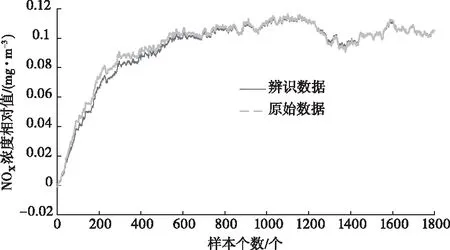
图12 260MW下辨识效果

对170MW和260MW两种典型工况下的原始数据值和辨识数据值进行误差分析，如表2所示，其中误差指标均方误差MSE和均方根误差RMSE公式如式(15)和式(16)所示

表2 两种典型工况辨识下的误差指标

(15)

(16)

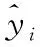
在MATLAB中Simulink平台搭建单回路PID控制和自适应遗传算法Smith预估补偿控制模型，NOx浓度设定目标值为40mg/m3，在700s时加入外来扰动，大小为20mg/m3，得到在170MW和260MW下的单位阶跃控制性能曲线，如图13和图14所示。

图13 170MW下控制性能曲线

从上升时间、调节时间、超调量和稳态误差四个方面对仿真结果进行定性分析，见表3和表4所示。

表3 170MW下控制性能指标

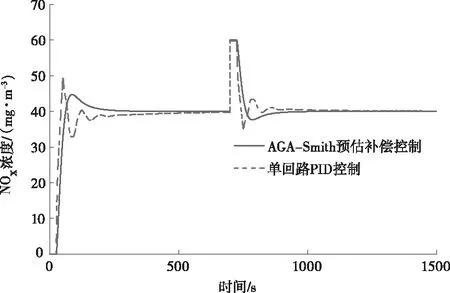
图14 260MW下控制性能曲线

表4 260MW下控制性能指标

计算结果表明，在两种典型工况下，AGA-Smith预估补偿控制下的超调量都比单回路PID控制下的超调量小，这在现场中控制对尿素流量的喷射量是相当有利的，且当加入外来扰动时，AGA-Smith预估补偿控制产生的超调量也小，调节速度变快。AGA-Smith预估补偿控制性能总体上优于单回路PID控制。

6 模型鲁棒性验证

虽利用IPSO算法辨识出SNCR脱硝系统尿素流量在典型工况170MW和260MW的传递函数模型，但现场模型参数并不是一直不变，受到床温、燃料量、加入石灰石量等因素的影响，模型参数势必会发生变动，现以170MW下SNCR脱硝系统尿素流量模型在系统阶次不变的情况下作为验证：

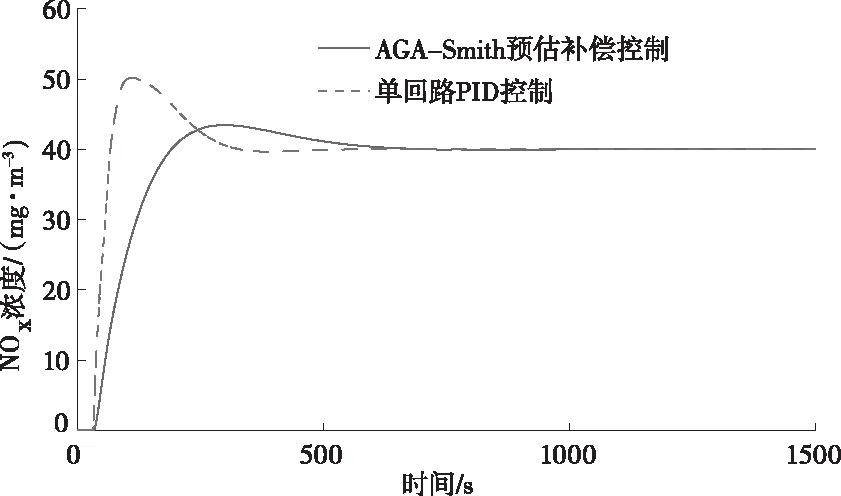
图15 K改变时控制性能曲线

图16 τ改变时控制性能曲线

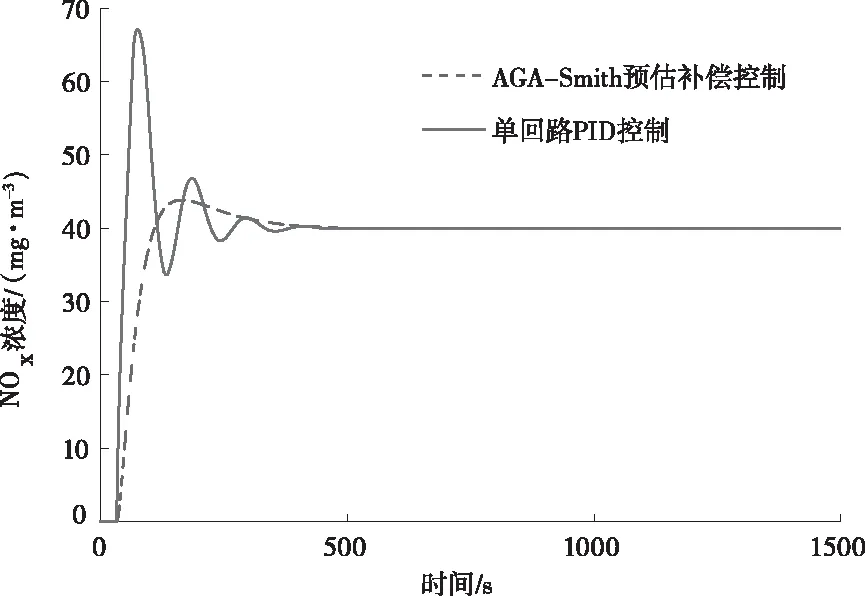
图17 T改变时控制性能曲线

当模型参数受到扰动发生变化时，可见单回路PID控制的模型适配能力低于AGA-Smith预估补偿控制的适配能力。

7 结论

1)针对目前存在的SNCR脱硝系统模型精度不高及脱硝控制效果不佳的现状，利用IPSO算法辨识出典型工况170MW和260MW下的尿素溶液流量到NOx排放浓度过程传递函数模型，在170MW和260MW下辨识输出值与原始输出值的均方误差值MSE分别为9.797×10-4、5.055×10-3；均方根误差值RMSE分别为3.13×10-2、7.11×10-2，利用IPSO算法辨识得到的模型精度较高。

2)在电站现场已有的单回路PID控制策略的基础上，将AGA-Smith预估补偿控制引入，通过优化Kp、Ki、Kd三个参数，得到了最佳的PID控制器参数；Smith预估补偿器的引入同时又可以克服脱硝系统模型大滞后特性带来的超调量大、不易控制等问题。仿真结果表明，AGA-Smith预估补偿控制效果总体优于单回路PID控制效果，抵抗外来扰动的能力更强。且AGA-Smith预估补偿控制模型适配能力强于单回路PID控制，为电站现场SNCR脱硝尿素溶液喷射控制提供了良好的参考。