基于CEEMDAN二次分解的风速预测
2023-03-29李颖智王维庆王海云
李颖智,王维庆,王海云
(新疆大学可再生能源发电与并网控制教育部工程技术研究中心,新疆 乌鲁木齐830047)
1 引言
我国鼓励发展邻近负荷中心的分散式风力发电,对分散式风电机组的风速进行超短期预测,便于电网调度,减轻分散式风机并网对电网造成的不利影响[1-3]。
为提升风速预测准确度,削弱风速特性带来的影响,文献[4]采用经验模态分解(empirical mode decomposition,EMD)与支持向量机(support vector machine,SVM)进行预测,EMD-SVM预测时准确度高、误差低;采用集合经验模态分解法(ensemble empirical mode decomposition,EEMD)进行数据处理,降低模型混频的概率,增强模型的自适应性[5-6];文献[7]采用自适应白噪声的完备总体经验模态分解(complete ensemble empirical mode decomposition with adaptive noise,CEEMDAN)进行预测,进一步提升了模型的鲁棒性。
为削减高频分量对预测的影响,降低预测数据复杂程度,文献[8]将风速预处理后的高频分量IMF1舍去,对剩余IMF分量进行预测。但直接舍去高频分量会导致数据信息缺失,进而影响预测准确度。因此,文献[9]对得到的高频IMF进行第二次分解,提升预测准确度。
针对最小二乘支持向量机(least squares support vector machine,LSSVM)模型预测效果受参数c,g影响较大的问题,本文采用均方差作为蝴蝶优化算法(butterfly optimization algorithm,BOA)改进LSSVM模型的适应度函数,提升LSSVM模型的预测精度。
综上,首先采用CEEMDAN将实测风速数据进行两次分解,充分挖掘数据信息,然后使用BOA改进LSSVM,提升风速预测模型精度。最后使用BOA-LSSVM组合模型进行风速预测。通过分析七种预测模型误差,验证基于CEEMDAN二次分解的BOA-LSSVM风速预测模型具有更好的预测效果。
2 算法原理
模态分解是处理历史数据,获取数据蕴涵信息的一种数据处理方法。采用EMD模型进行数据处理时,虽然提升了数据的准确性,却不能忽视其具有混频的弊端[4]。EEMD对数据进行处理时,虽可通过增添的白噪声增强模型的自适应性,提升预测准确性,但有概率产生虚假分量[5-6]。采用CEEMDAN对风速数据进行处理时,在分解过程中增添了有限次数的自适应高斯白噪声,改进EMD模态混叠的缺陷与EEMD导致的虚假分量的弊端。与此同时,相较于采用VMD算法进行第二次分解,CEEMDAN算法通过添加自适应白噪声,可以避免出现因VMD没有预设好合适的分解次数K,致使分解的IMF出现间断情况[7]。因此,本文采用CEEMDAN对历史风速数据进行二次分解。
CEEMDAN算法的运行过程如下:
1)对信号S(t)+ε0ni(t)重复运行N次分解运算过程,得到IMF1:
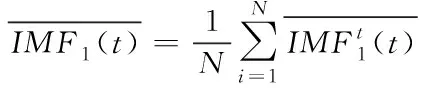
(1)
2)运算出的首个余量信号:
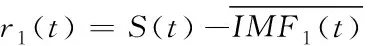
(2)
3)对信号r1(t)+ε1E1(ni(t))进行运算,得到IMF2
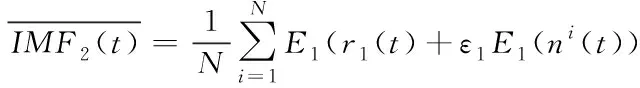
(3)
4)计算第l个残余信号,l=2,…,L
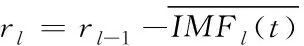
(4)
5)反复运算步骤3),得出第l+1个IMF

(5)
6)重复运算步骤4)和5),原始信号最终分解为
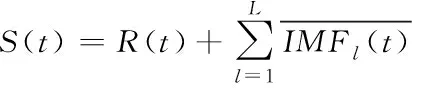
(6)
2.1 排列熵
排列熵(permutation entropy,PE)不仅对数据波动感知敏锐,能够降低不确定性估计,还具有运算简易,不易受噪声干扰的特点。通过PE衡量IMF的随机程度时,PE数值越高表明IMF越随机混乱[10-13]。根据PE的特性可知,若IMF的PE值近似,则表明分解得到的IMF内部混杂程度类似。本文采用PE量化各IMF的随机程度,对比各IMF的PE数值,将混杂程度相近的IMF进行重构,并采用CEEMDAN进行第二次分解。
排列熵算法运行过程如下:
1)对序列{s(n),n=1,2,…,N}重构,得到重构矩阵D:
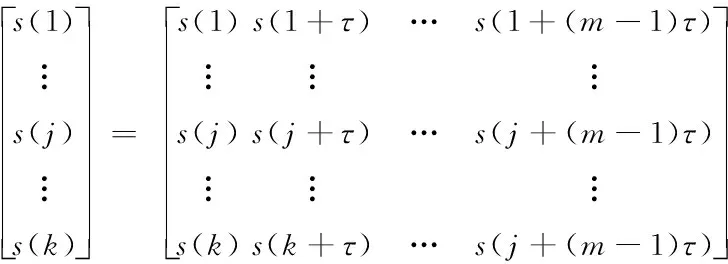
(7)
式中:m—嵌入维数;τ—延迟时间
2)对各个重构向量进行升序排序
s[j+(kj1-1)τ]≤s[j+(kj2-1)τ]≤…
≤s[j+(kjm-1)τ]
(8)
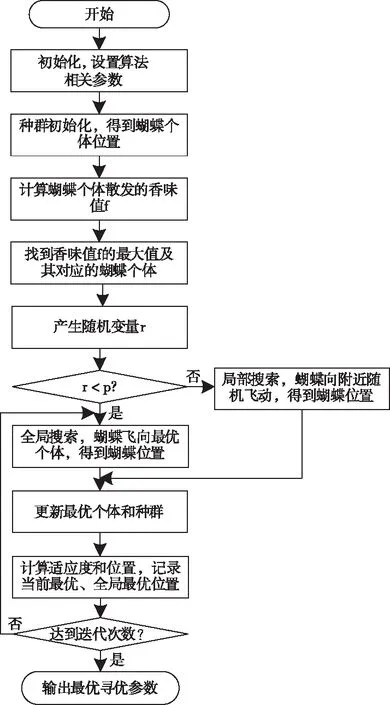
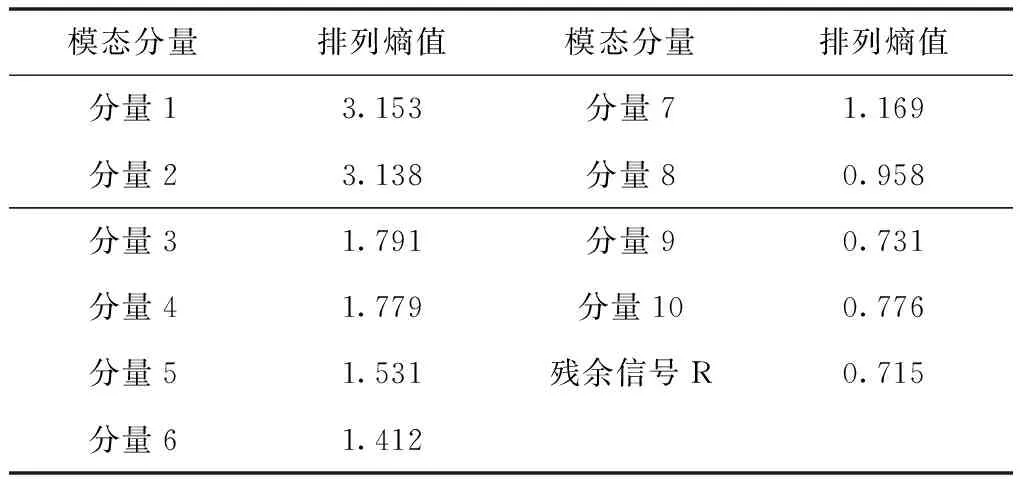
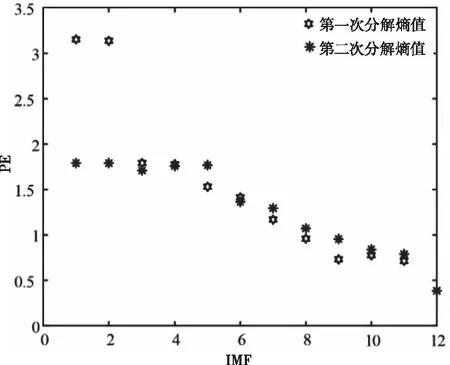
若s[j+(kj1-1)τ]=s[j+(kj2-1)τ],则比较所在列的kj1,kj2,若kj1 3)重构后得到矩阵S(i)={j1,j2j3,…,jm},式中m=1,2,3,…,N且N≤m!。故有m!种符号序列。 4)序列s(n)的PE为 (9) 式中:Pj—每种序列出现概率。 2.2.1 支持向量机算法 SVM是一种适用于历史样本数目较少且泛化能力好的预测算法[14]。SVM算法函数模型推导过程具体如下 (10) (11) 2.2.2 最小二乘支持向量机 最小二乘支持向量机将SVM模型中的不等式约束优化为等式约束,提升了模型的运行效率[15-16] LSSVM的约束及优化目标的函数模型为 (12) LSSVM的Lagrange函数 b+ξi-yi} (13) 通过对式(13)中的ω,b,ξ,a,求偏导,消去ω和ξ,得到的LSSVM预测模型为 (14) SVM共有四种不同的核函数,RBF核函数在SVM中使用次数最频繁,相较于其它几种核函数,RBF待优化的参数少,适用范围广。因此,本文选取的核函数K(x,xi)为RBF核函数。本文选取的核函数K(x,xi)定义为 (15) 2.2.3 蝴蝶优化算法 BOA受蝴蝶寻找食物和寻觅配偶的行为启发,通过模拟蝴蝶搜寻气味的习性,提出了蝴蝶优化算法[16]。BOA算法大范围的全局搜索和密集局部搜索两种搜索方式组成。全局搜索是指蝴蝶嗅到香味时,指定位置靠近的行为。局部搜索是指蝴蝶觉察不到附近存在气味后,进行随机移动搜寻的行为。BOA通过上述两种搜寻方式向目标进行移动寻优。BOA寻优过程如下: 蝴蝶产生香味公式如下 (16) 式中:c—感官因子;I—刺激强度;a—幂指数。 通过切换概率p,实现BOA搜寻方法的转变。 全局搜索公式如下 (17) 局部搜索公式如下 (18) 2.2.4 BOA优化LSSVM 针对LSSVM的存在预测效果易受c,g参数影响的问题,本文将均方差作为参数c,g寻优的适应度函数。通过BOA对LSSVM的c,g进行寻优处理,进一步提升LSSVM对风速的预测准确度,适应度函数为: (19) 蝴蝶优化算法优化过程见图1。 图1 BOA算法流程图 本文采用均方根误差(RMSE)、平均绝对误差(MAE)、均方误差(MSE)对预测模型准确性进行对比研究。 (20) (21) (22) Step 1:采用CEEMDAN将风速的实测数据分解为IMF。 Step 2:计算各IMF的排列熵,量化各IMF的随机程度、复杂程度。 Step 3:对熵值进行对比研究,选出熵值大的分量,采用CEEMDAN对其进行第二次分解,降低其随机性。 Step 4:通过排列熵量化第二次分量的复杂程度,根据排列熵数值高低对所有IMF分量执行IMF合并操作,以此减轻由IMF数量增加,导致计算时间延长的压力。 Step 5:使用BOA-LSSVM预测合并后的IMF,得出风速预测结果。 Step 6:累加各BOA-LSSVM风速预测结果。 图2 预测模型流程图 选取2019年8月25日至9月5日新疆某风电场的实测风速数据,进行超短期风速预测。数据每10分钟进行一次采样。对采集数据的异常点进行排除后,选取前1653个实测风速数据用于训练,后30个实测风速数据用于对比研究,通过仿真验证所提模型的可行性。 图3 原始风速序列 使用CEEMDAN处理风速数据,得到的各IMF为图4所示。 图4 CEEMDAN分解结果图 为了降低因数据随机程度高导致的预测误差,采用PE量化各IMF的随机程度,计算出的各模态分量的排列熵值见表1。 表1 CEEMDAN获得的各模态分量的排列熵值 根据表1可知,CEEMDAN分解得出的分量1与分量2排列熵熵值最高,随着分解次数的增加,分量的排列熵熵值逐步降低。二次分解过程具体过程如下:首先,选取第一次分解中PE远高于其它IMF的IMF1与IMF2进行数据相加;其次,采用CEEMDAN对重构的IMF数据进行第二次处理;最后,计算得出第二次分解各IMF的PE数值,两次分解获得的IMF排列熵见图5。 图5 各分量排列熵 通过图5可知,随着原始风速数据的分解,各IMF分量的PE的随机性逐步降低,并且CEEMDAN第一次分解与CEEMDAN二次分解获得的IMF中部分分量的PE值相近。 为提升BOA优化LSSVM模型的运行效率,减少预测误差,采用熵值相近原则对熵值相近的IMF进行重构[6]。选择将第一次分解得到的IMF3-5与第二次分解得到的IMF1-5重构为S1;将首次分解得到的IMF6-7与第二次分解得到的IMF6-8重构为S2;S3由第一次分解得到的IMF8-10、残余信号R与第二次分解得到的IMF9-11构成;S4由第二次分解的残余信号R2构成。 本文采用基于CEEMDAN两次分解的BOA优化LSSVM模型进行超短期风速预测。为了证明本文模型的有效性,将基于CEEMDAN两次分解的BOA-LSSVM方法的预测结果与采用另外六种方法求出的预测值进行对比,七种模型风速预测结果见图6,七种模型的误差对比见表2。 表2 七种预测模型风速预测结果误差 图6 七种模型风速预测结果 通过对比研究误差对以上七种风速预测模型的进行评估: 对比使用EMD、EEMD、CEEMDAN三种数据处理方法时,发现使用CEEMDAN获得的RMSE、MAE、MSE均是最小,验证本文所用分解方法的合理性; 通过对比CEEMDAN-BOA-LSSVM与未经优化的CEEMDAN-LSSVM风速预测的误差可知,采用BOA优化后的预测误差RMSE降低0.0639、MAE减小了0.0847,MSE误差减少了5.37%,验证采用BOA优化LSSVM能够改善模型,提升预测精确度。 根据本文与CEEMDAN-BOA-LSSVN的预测曲线,以及表2的误差数据可知,使用相同方法对同一组风速实测数据进行预测时,二次分解后再预测的RMSE、MAE、MSE都优于仅进一次分解的预测误差值。相较于CEEMDAN-BOA-LSSVM的误差,本文方法的RMSE降低了0.1423、MAE减少了0.1409、MSE减少了9.04%。 通过仿真验证可知,本文所提模型在上述七种模型中预测误差最小,预测效果最好,取得的拟合效果最佳,可以提升风速预测的准确度。 本文基于CEEMDAN对风速进行两次处理再通过BOA-LSSVM对风速进行超短期预测,通过对比预测数据与实测数据误差,得出以下结论: 1)通过排列熵对序列的随机性进行评估,识别需进行二次分解的序列。对数据进行两次分解,能够降低数据的随机程度,提升预测结果的准确性。 2)将均方差作为优化支持向量机的适应度函数,解决了LSSVM参数寻优效率低的问题,进一步提升预测结果有效性。 3)通过对比七种预测模型的预测结果,证明本文所提的预测模型进行风速预测的可行性。提高分散式风机的风速预测准确度,对提升分散式风机能源的利用率有重要意义。
2.2 最小二乘支持向量机及其参数优化
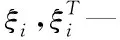
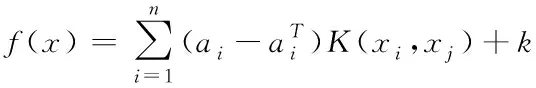

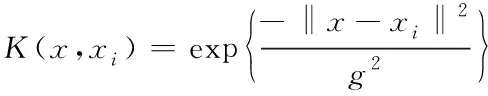
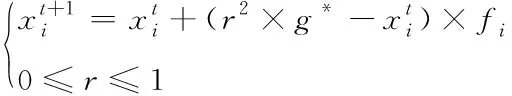

2.3 误差评估


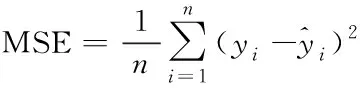
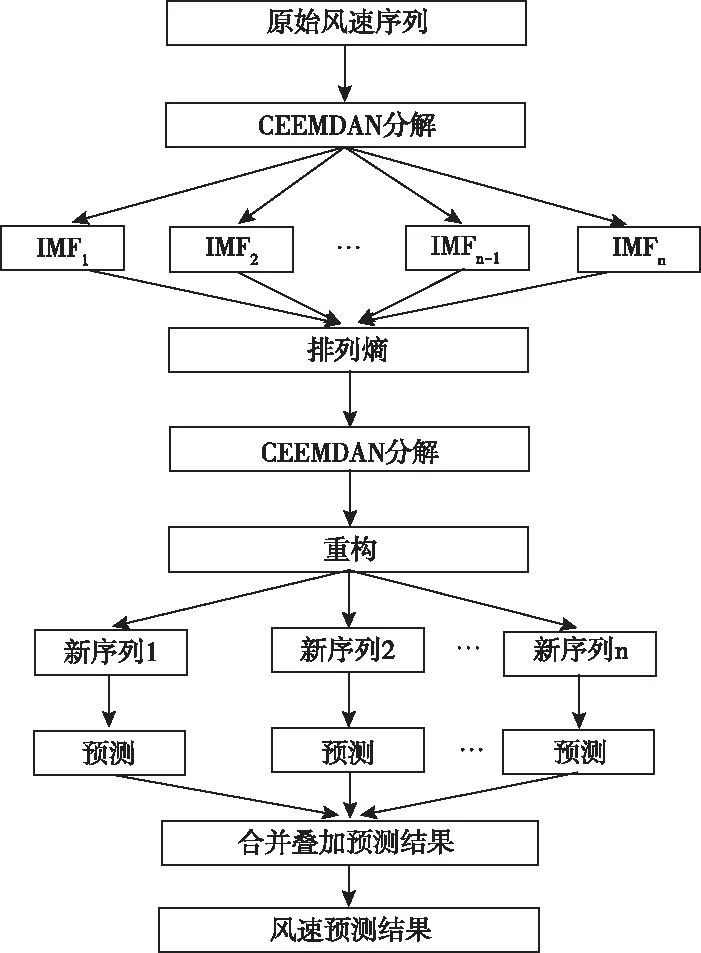
3 基于CEEMDAN两次分解的BOA-LSSVM预测方法
4 实例

4.1 风速数据分解
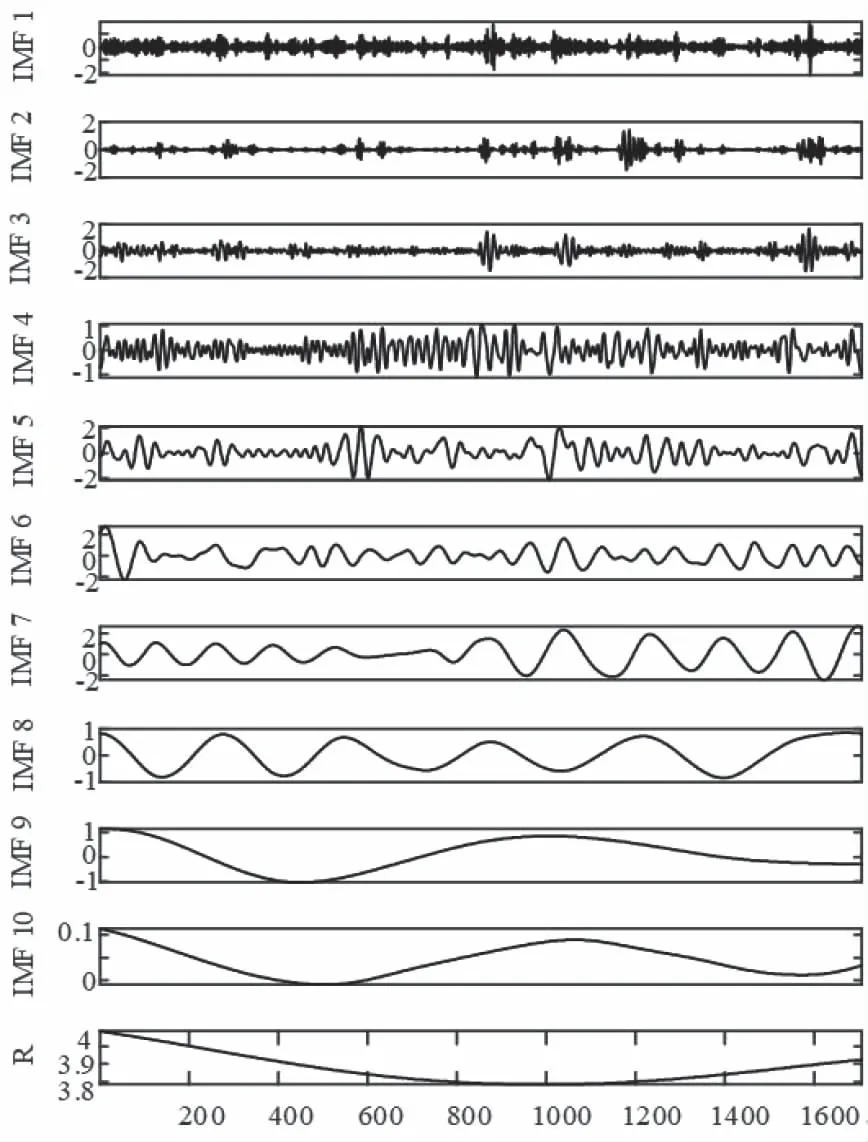
4.2 分解数据处理
4.3 风速预测及模型结果分析

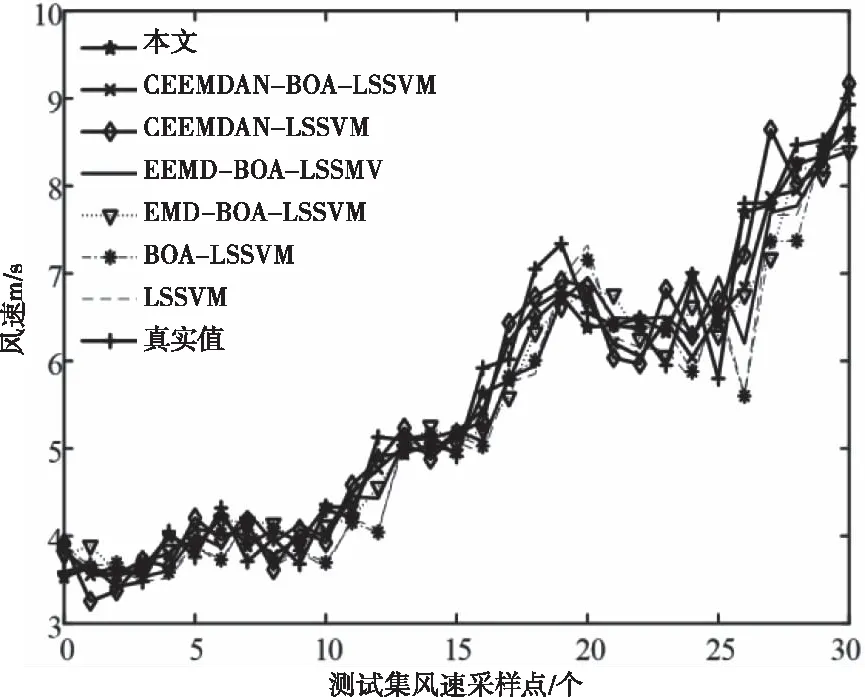
5 结论
