基于密度峰值聚类的超短期工业负荷预测

金维刚，李 锋，周良松

(1. 国家电网公司华中分部，湖北 武汉 430077；2. 华中科技大学电气与电子工程学院，湖北 武汉 430074)

1 引言

2015年国务院发布的第9号文件提出了关于进一步深化电力体制的改革，促进我国电力行业又好又快的发展的精神。努力解决电力行业的突出矛盾和深层次问题，并且要尽力推动结构转型和产业升级[1]。随着我国新一轮电力体制改革的实施，挖掘用户用电数据和用电行为，掌握用户用电规律，进行精准的负荷预测具有重要意义[2]。

水泥行业是一类电力高耗能产业，其负荷总量大，波动性强，具有一定的冲击负荷，对电力系统具有较大影响，威胁着电力系统安全稳定和电能质量。因此，要科学的对影响水泥行业电力负荷的因素进行分析，达到提高负荷预测的准确性的目的，并以此为依据对生产方式进行调整，保证电力系统的稳定运行。

目前，针对高耗能的工业用户负荷预测主要集中在中长期负荷预测上，文献[3]提出了针对高耗能工业用户的负荷波动特点用分类建模的思想进行负荷预测模型的构建，但是其分类原则依靠主观判断。文献[4]使用粒子群算法优化后的最小二乘支持向量机预测模型对某工业用户进行了中长期负荷预测。文献[5]、文献[6]均中使用了FCM聚类法，研究工业用户的负荷特性，但是FCM聚类算法容易陷入局部鞍点，所以预测精度不高。文献[7]采用的遗传膜优化BP神经网络预测模型存在较大主观性，且预测精度不高。

针对以上问题，本文针对以水泥工业为例的高耗能工业用户提出了一种基于密度峰值聚类的GRNN神经网络的超短期负荷预测的方法，区别于其它预测方法的是，本文中使用聚类效果更佳的密度峰值聚类算法对负荷数据进行聚类分析，再对聚类所得类簇分别建立预测模型，预测精度更高，对于指导用户合理购电更具指导意义。

2 数据预处理及分析

2.1 数据预处理

本文中采用的负荷数据来源是某市某水泥公司，通过关口表采集到的数据。时间跨度是2018年5月1日到2018年12月31日，共计245天，每15分钟进行一次数据采集，每日共计96个点。删除含有异常值的26天的数据，并将数据归一化到区间[0，1]中。

2.2 数据分析

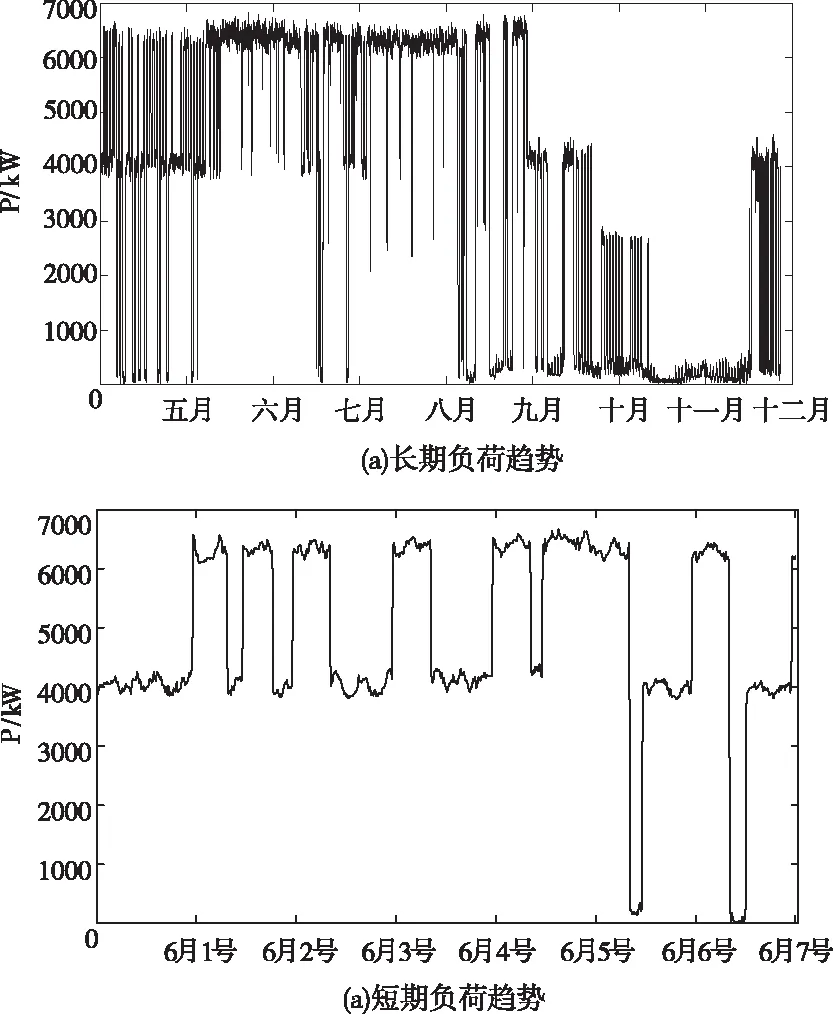
图1 原始负荷曲线

对数据进行时间序列分析如图1将原始数据分为长期趋势和短期趋势进行分析，可以看出水泥行业的负荷特点是日负荷曲线波动很大，每日曲线的形状也有一定的差异，有时负荷还会接近0。但就每天的总体趋势来看，日间负荷会出现低谷，高峰出现在夜间，原因是用户根据分时电价制定生产计划。在保证正常生产状况的情况下，峰时电价时间段尽可能减少用电，谷时电价时可以满负荷运作，以达到减小生产成本的目的。基于这种情况。考虑对用户的负荷曲线进行聚类研究，然后进行负荷预测。

3 密度峰值聚类算法

2014年，亚历克斯·罗德里格斯(Alex Rodriguez)和亚历山德罗·莱奥(Alessandro Laio)在Science上发表文章，提出了一种新的聚类算法，称为“密度峰值聚类”。该算法通过计算数据点之间的距离识别非球状类簇，与FCM聚类方法相比，该算法可以自动确定聚类中心和聚类数，并快速搜索并找到数据点的密度峰值[8]。可以得到更精准的类簇，用以分析用户用电行为。

3.1 算法原理

密度峰值聚类算法的核心是对聚类中心的定义，聚类中心有两个重要的特征：

1)聚类中心具有较大的自身密度，即聚类中心的密度大于包围聚类中心的“邻居”的局部密度[8]。

2)聚类中心和局部密度比它更大的数据点之间的距离相对来说会更大。

假设待聚类的数据集为X={xi}N，其对应的指标集为IX={1，2，…，N}，用dij表示数据点xi与xj之间距离，对于数据集X中的任一数据点xi，定义两个重要的参数：局部密度ρi和距离δi。

局部密度ρi通常采用截止核函数(Cut-off kernel)或者高斯核函数(Gaussian kernel)进行计算，但Cut-off kernel为离散值，而Gaussian kernel为连续值。考虑到本文中原始数据为连续值，故采用高斯核函数来计算局部密度。

(1)

式中，dij表示数据点xi与xj之间的距离，dc表示截断距离，ρi表示数据集X中与数据点xi的距离小于dc的点的个数。其中dc需要人为指定，对于大型数据集，密度峰值聚类算法对于dc的选取具有鲁棒性[12]。

ρq1≥ρq2≥…≥ρqN

(2)

定义距离δi为

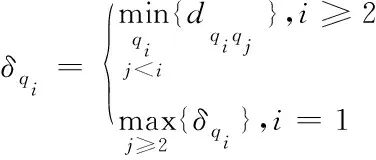
(3)

运用式(1)(3)计算可以得到各数据点xi∈X的(ρi，δi)，然后在二维坐标图中将所有数据点表示出来得到决策图。选择聚类中心的原则是该数据点的ρ值和δ值均比较大。而剩余的数据点会在确定聚类中心之后被分派到距离最近的自身密度更高的数据点所在类簇中。

对于在决策图中难以用肉眼判断出聚类中心的情况，定义一个综合考虑ρ值和δ值的指标γi

γi=ρiδi，i=IX

(4)

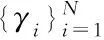
3.2 两个距离dij和dc的选取

3.2.1距离dij的选取

距离dij用于评价不同样本之间的差异度[9]，由于已经对原始数据进行归一化处理，因此，只需要考虑不同样本之间在空间距离上的数值差异，在此引入欧式距离，其表达式为

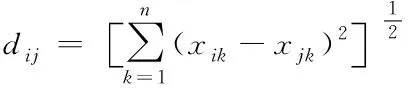
(5)

式中，xik和xjk为样本xi和xj的第k维元素。

3.2.2截断距离dc的选取

首先计算样本之间的欧氏距离得到N个距离值，然后将距离值升序排列为d1≤d2≤…≤dN。截断距离dc=dn，其下标n=[0.02N]([ ]为取整函数)。

4 密度峰值聚类

4.1 决策图

将第一节中归一化后的数据，共计219天，每天96个点构成的219×96维的负荷特征向量进行平滑处理然后进行聚类，得到如图2的结果。图(a)中同时具有较大ρ值和δ值的点共有4个，图(b)中显示这4个点与其它点在γ≈0.13处有明显跃变。所以聚类中心共有4个，聚类数为4。

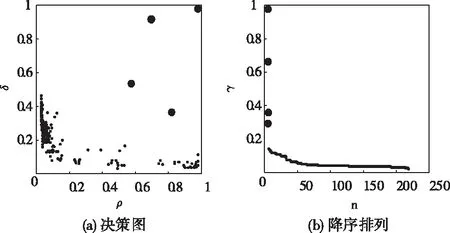
图2 聚类结果

4.2 类簇分析

各类簇反映的日负荷波动情况如图3所示，由于已对数据归一化到区间[0，1]，所以纵轴刻度为[0，1]。

图3中的四种波动情况基本涵盖了水泥行业的在各种生产状况下的负荷波动情况。类簇1反映了减产甚至停产的负荷情况，类簇2和类簇4反映了正常生产情况下采用避峰的手段降低用电成本的负荷特性，类簇3反映了企业全天候满负荷生产时的负荷特性。

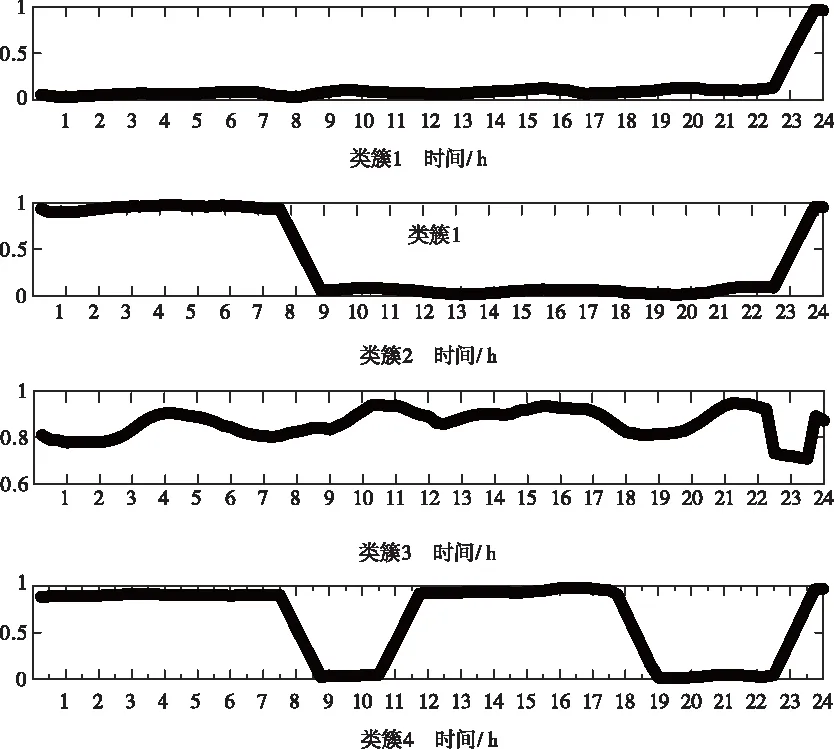
图3 类簇图

5 广义回归神经网络

广义回归神经网络是一种非线性映射能力更强，容错性更好，鲁棒性更高的改进型径向基函数[12]。而且在样本数较少的情况下依然能有较高的预测精度。鉴于本文中的负荷数据较少，所以选用广义回归神经网络进行预测。

5.1 广义回归神经网络结构

本文中所使用的广义回归神经网络结构共四层，分别是输入层、输出层、模式层和输出层。输入层和输出层均设96个神经元。

5.2 神经网络训练

5.2.1 K折交叉验证

由于部分类簇的样本数量较少，所以本文采用交叉验证的方法进行神经网络的训练[13]。根据每一类簇的具体样本数进行K折交叉验证，将样本分割成K个子样本，轮流将一个子样本作为测试集，剩余的K-1个子样本作为训练集，重复K次。再针对每一类簇建立神经网络预测模型，求得最优输入输出。

5.2.2 最优SPREAD值的选择

SPREAD值是调节广义回归神经网络的重要参数[10]，其合理的选值是否合理直接影响着预测结果的精度。SPREAD值越大，就越能保证神经元能对输入向量所覆盖的区域都能产生对应，但是SPREAD值如果太大，数值计算就会变得较为困难，同时太大的SPREAD值会使神经网络在数据样本的逼近结果出变得光滑，导致误差的变大。所以本文为了对数据进行更为严格的拟合，通过循环选取SPREAD值的方法，选择最优SPREAD值。

以比较有代表性的类簇2为例，共有48个样本，进行4折交叉验证，设置SPREAD值的取值范围为[0.1，2]，步长为0.1，以均方误差MSE作为输出结果的评价指标。交叉验证结果见表1

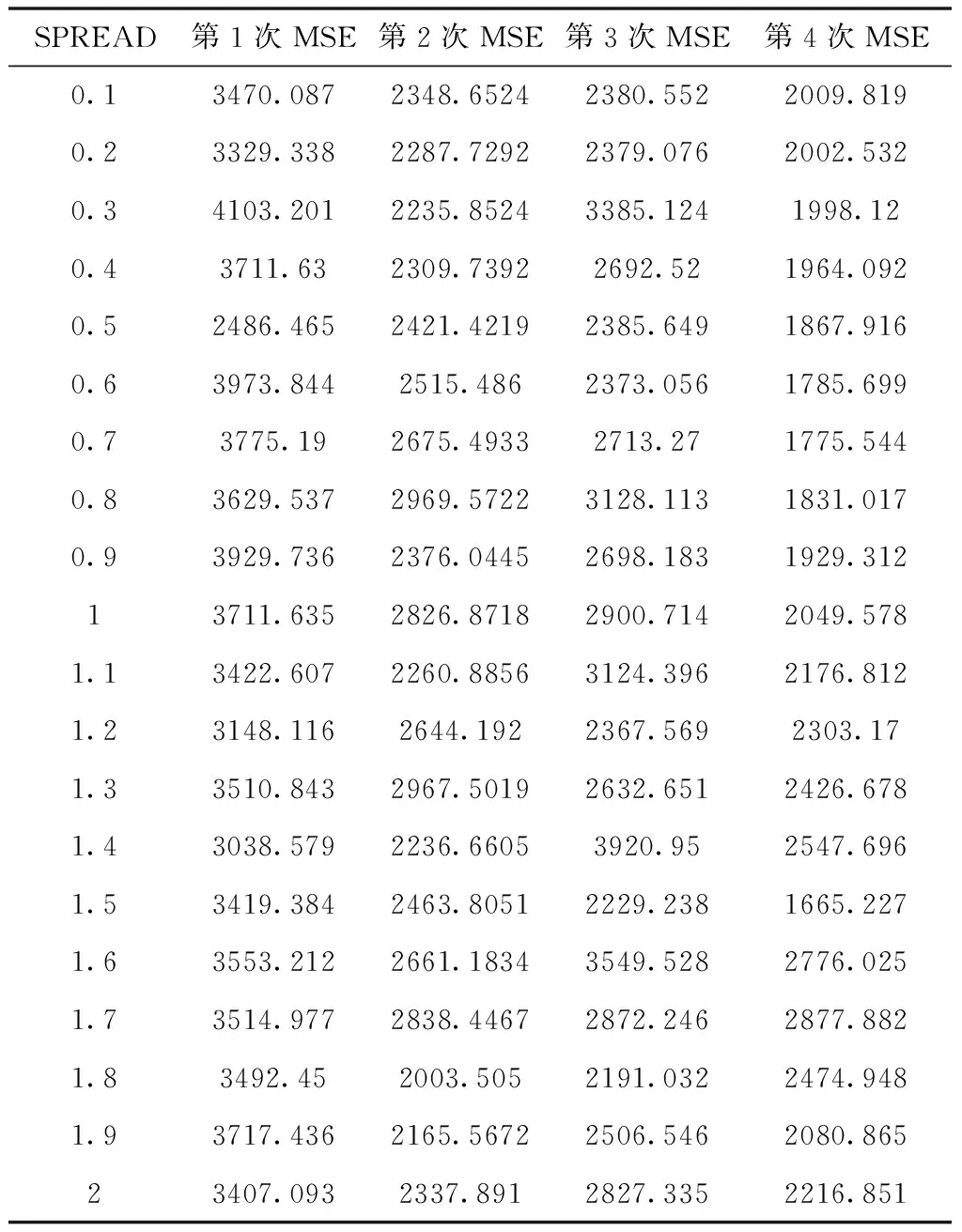
表1 类簇2交叉验证结果

由表1得交叉验证在第4次交叉验证，SPREAD值取1.5时MSE的值最小。所以对于类簇2采用第5次验证时所用的训练集，SPREAD值取1.5，构建的GRNN神经网络模型的预测效果最好。针对其它3个类簇构建GRNN神经网络预测预测模型时也遵照此方法选取最优训练集和最优SPREAD值。

6 算例分析

本文选用某市某水泥企业2018年5月1日至12月31日的负荷数据为基础，对未来全天每15分钟一个点进行负荷预测。分别与密度峰值聚类+BP和FCM+GRNN的预测模型进行对比。

6.1 预测结果分析

本文中所采用的评价预测精度的指标为平均绝对误差百分比(MAPE)和均方根误差(RMSE)。

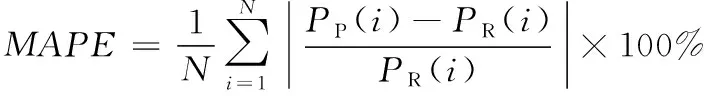
(6)

(7)

式中，PP(i)表示企业负荷预测值，PR(i)表示企业负荷实际值。N=96，表示一天的预测点个数。

从4个类簇中分别随机选取2018年12月4日(类簇1)、2018年12月30日(类簇2)、2018年3月19日(类簇3)和2018年6月1日(类簇4)，作为实测曲线与预测曲线进行对比，见图4，预测误差统计结果见表2。可以看出，本文提出的预测方法在各个类簇中均表现较好，预测精度较高。但是对于2018年3月19日14时前后的时刻和2018年6月1日8时左右的时刻的预测，精度较低。且均是未能将突然出现的负荷波动预测出来，但是对于类簇1中的剧烈波动却能有较好的预测结果。原因是类簇1的样本数量较多，而类簇3和类簇4的样本相较偏少。对于类似水泥行业的大型工业用户来说，在生产过程中，由于人为因素，或者市场，政治因素导致的用电负荷出现剧烈波动的情况时有发生，那么对于在小样本下如何提升对产生剧烈波动的负荷特征的提取与预测是下一步要研究的重点。

表2 预测效果评价

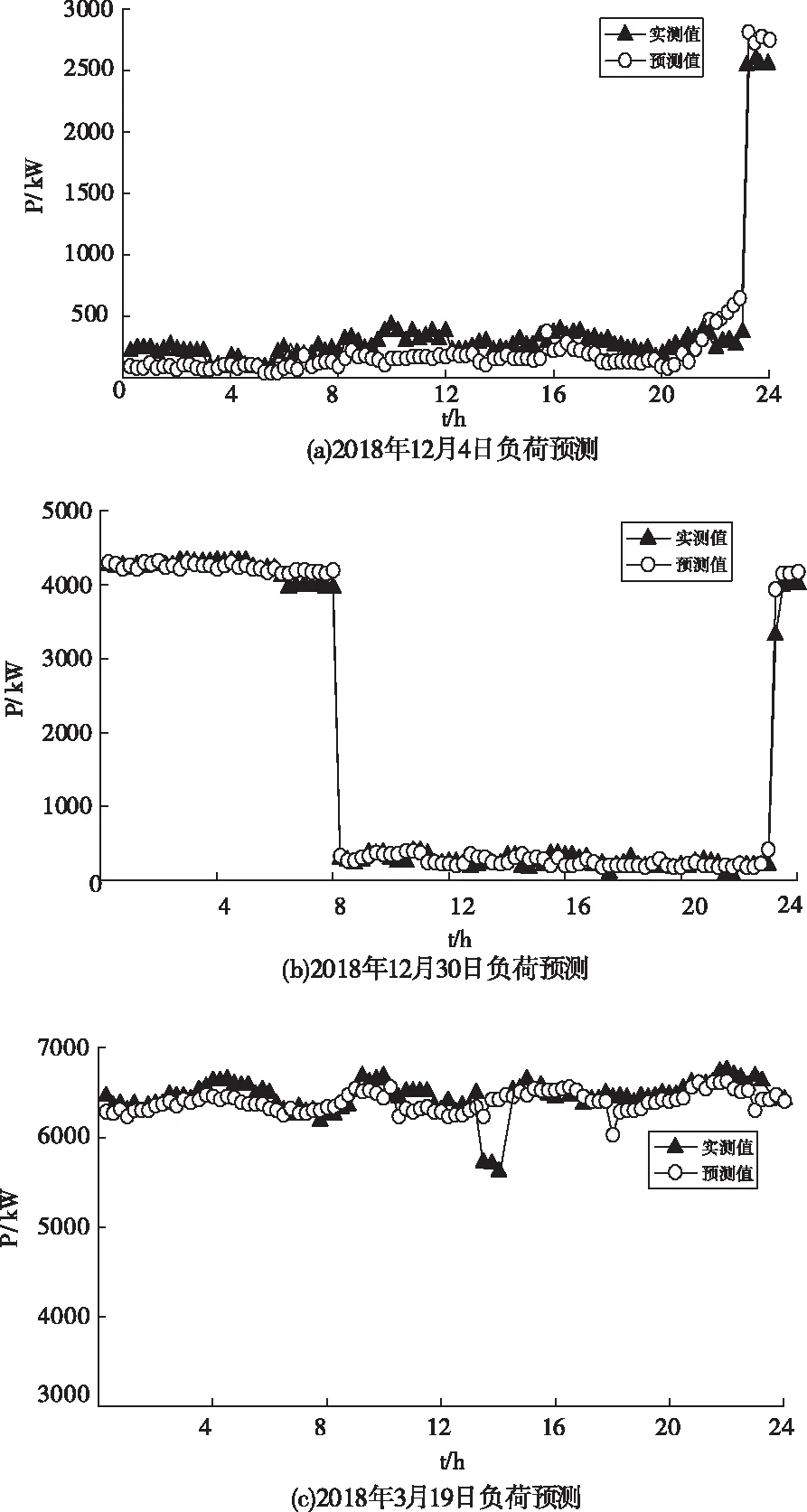
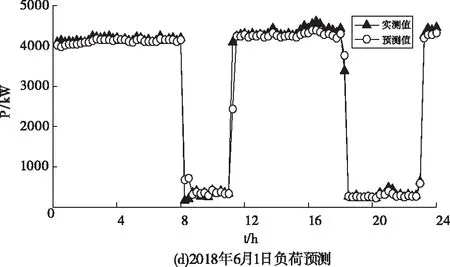
图4 负荷预测结果

6.2 预测模型对比

将2018年12月30日作为预测日，用相同的数据集，再分别使用密度峰值聚类+BP神经网络预测方法和FCM+GRNN预测方法进行预测，同样使用MAPE和RMES作为评价指标。预测效果指标模型对比结果见表3，各模型预测结果对比图见图5，为保证图片清晰度，仅选择每日24个点进行绘图。从对比结果中可以看出，使用本文提出的方法可以更好地提高预测精度。

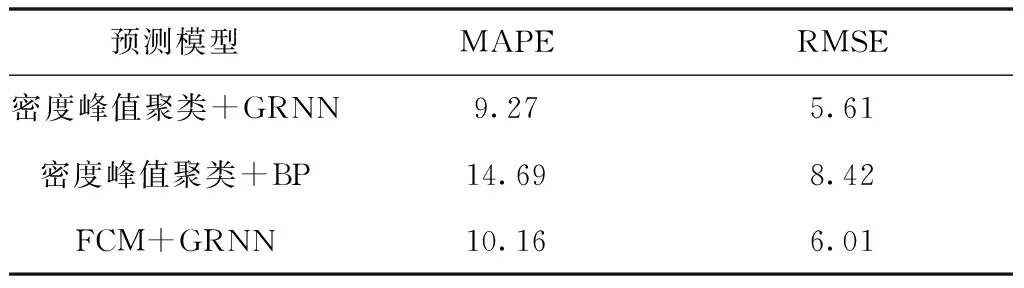
表3 预测模型对比结果

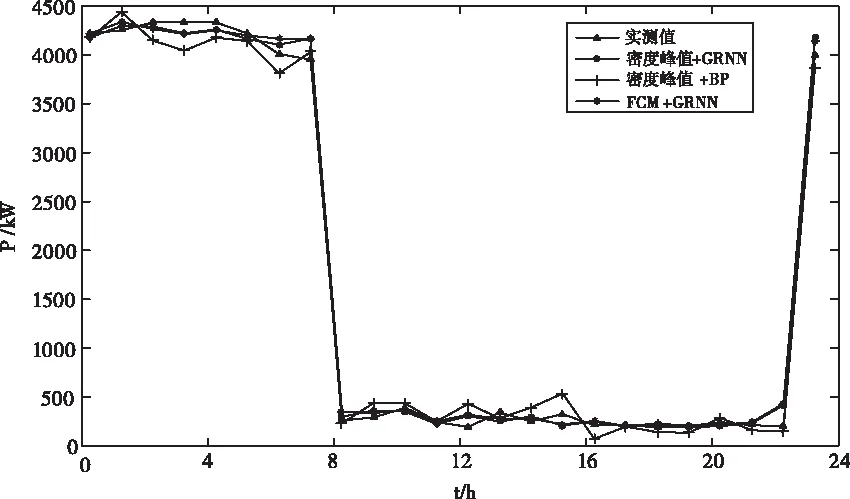
图5 2017年12月30日各模型预测曲线

7 结论

本文针对水泥行业提出了一种超短期负荷预测的方法，采用密度峰值聚类方法对负荷数据进行聚类，再针对不同类簇分别建立GRNN负荷预测模型，使用Matlab软件得到仿真结果，预测精度可以达到9.27%，现有以下结论。

1)密度峰值聚类相较于传统聚类方法可以更准确的对原始负荷数据进行聚类，且不需要人为指定聚类中心和聚类数，在对大用户进行负荷预测之前对原始数据进行聚类方面具有较好的适用性。

2)构建GRNN神经网络负荷预测模型时，根据不同类簇样本数的不同，选择K折交叉验证训练模型，循环选取SPREAD值，然后去的最优值构建GRNN神经网络。预测精度较高，能够更好地指导用户合理购电。