模型Sloppy属性及相关特性综述
2023-03-29王红,康玲
王 红,康 玲
(1. 大连东软信息学院计算机学院,辽宁 大连 116023;2. 大连东软信息学院 软件学院,辽宁 大连 116023)
1 概述
近年来随着计算能力的进步,数学模型的规模以及描述范围不断拓宽。大量描述各种现象的复杂模型不断出现,从生物化学反应网络、到气候变化模型再到经济发展动态模型,依托数学模型进行科学探究已经成为当今的核心关注点[1,2]。这些模型的复杂性呈现出很多新的特征也为基于这些模型开展科学研究提出了新的问题和挑战。
1.1 Sloppy模型
数学模型中通常包含大量的未知参数,由于费用、时间或实验条件等因素的制约,这些参数的值只能通过和已有实验数据的拟合来确定,通常把这一过程称作模型校准[3]。通过模型校准,原则上参数可以被实验数据唯一确定[4]。但有些模型中的某些参数值,即使给出再多的实验数据依然不能唯一被确定[5]。这主要是因为模型中不同的参数组合对模型的输出呈现出不同数量级的影响[6],进而表现为如下特征:微小扰动部分参数组合会使模型输出变化非常大,而大规模扰动某些参数或其组合,模型输出却没有明显变化。因此所谓的sloppy模型是指模型的行为只被几个有限参数组合所控制的模型。小扰动大变化的参数组合是stiff参数(属性)组合,而大扰动小变化的参数组合是sloppy参数(属性)组合[7]。
有人认为sloppy属性和鲁棒性(robustness)的表现很相似。但从传统概念上来讲,二者截然不同。当一个系统被认定为具有鲁棒性特征时,意味着有一个特定的定量行为对于特定的扰动不敏感,且这种扰动可以是参数值的变化、系统外界影响因素的变化甚至系统结构的变化[8]。而sloppy属性则相反,当关注系统的定量行为时,它的敏感性和参数的组合变化相关。甚至一个sloppy模型可能对于每个参数的变化都不具有鲁棒性[9]。
但从运作原理上来看,sloppy属性和鲁棒性之间又有着密切的联系。比如许多生物系统规模大且形式复杂,某些构件相对于功能实现来说还有冗余,但这种冗余却是系统应对内外环境的突变或噪声而产生的鲁棒性反应。因为从网络动态性与网络构成关系角度来看,这种冗余是当构件具有sloppy属性时,网络所呈现出的合作响应模式[10]。
1.2 Sloppy属性研究意义
Sloppy属性广泛存在于系统生物学模型、加速器物理学模型、放射性衰变系统、临界模型、昆虫飞行模型等诸多领域模型中[11]。
近年来,模型中sloppy属性的存在也为研究系统背后的运行机理提供了新的研究视角。如在生物领域可以基于sloppy属性,研究神经元活动随时间发展的进化规律、神经网络中的可塑性调整机制及运动过程中显著性变量的稳定性控制问题、预测肌酸肌酶对ATP组的催化反应效果,以及探求生物神经网络初始过密的凸起和神经元剪枝优化背后的运作机制;也可用于系统动态进化的强壮性和组件衰退性背后的一般理论研究;在电子能源领域还可以利用模型的sloppy属性特征,研究存储环在加速时如何降低发散率进而提高衰减环的亮度,以及在震动、电子环境和量子机制等自由度不可控条件下,如何提高能量传输的有效性及可靠性问题。
Sloppy属性的存在也为研究模型与模型属性的关系提供了可能。如将sloppy属性和敏感度分析[12]、实验设计[13]、系统及参数可认定[14]、系统强壮性以及反向工程[15]等方面的研究建立起了联系。因为sloppy属性体现的是模型对于外部环境扰动及内部构建交互变化的强壮性,而该属性是生物集体得以进化的关键特征,因此在计算生物学领域,sloppy属性是否存在也成为判断构建的生物模型是否具有实际可行性的重要依据之一。
此外,sloppy属性的存在也为模型的参数估计以及模型预测研究带来挑战。由于sloppy属性的存在,使得模型中参数估计问题演变成不适定问题且模型中的参数不能逐一被认定[11],即使可以得到对应参数的估计值,但其置信区间也会变大[9]。使用sloppy模型进行功能预测时可能会引发预测结果的统计性错误[9,16]也为分析模型预测不确定性引入计算困难。因此,sloppy属性的存在也促进了相关优化算法的研究,如对优化算法提出改进,基于几何原理理解提出更有效更适用的计算方法[6]等。
1.3 Sloppy属性判定依据


(1)
该损失函数在参数的最优拟合点的曲率就是Hessian矩阵的定义,如式(2)的形式。
(2)
如果此时Hmn的最大特征值λmax与最小特征值λmin的度量差超过三个数量级时(如式(3)所示),则可判定该模型具有sloppy属性[14]。

(3)
因为很多模型中的参数有不同的度量单位且变化范围大,为了消除相对变化对参数值的影响,在计算Hessian矩阵的时候通常可以采用log10对数的形式,如式(4)所示[17],这就是特征值谱的对数尺度宽度。
wλ=log10CF
(4)
当w≥6时模型也可被认定为sloppy模型,而非sloppy模型的宽度一般约等于2。此时参数的stiff和sloppy属性可以通过分析Hessian矩阵Hmn的特征值进行确定。因为Hessian矩阵具有正定及对称的特征,因此它的特征值和特征向量都是实数。分析Hessian矩阵对应的近似曲面可以看出和系统响应的偏离。该界面是一个Np维度的椭球体,Np是模型中参数的数目,椭球的主轴是Hessian矩阵的特征向量,椭球沿着每个主轴的宽度正比于对应特征值λi平方根的倒数,如式(5)所示[17]。
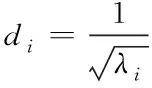
(5)
其中最窄的轴对应stiff属性对模型行为有很大影响,最宽的轴对应sloppy属性对模型行为有微小的影响[4]。
对式(2)做近似处理,省略掉第二部分,就得到了Fisher信息矩阵[18],如式(6)所示,其中J 是衡量参数敏感度的Jacobian矩阵。
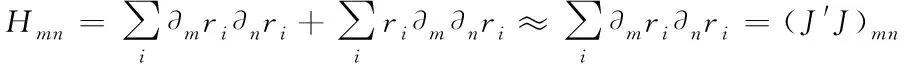
(6)
Dufresne研究小组组合代数与几何知识,在参数空间引入等价关系,借助等价关系给出sloppy属性的统一数学框架,将其所能描述的模型类型也从依赖于时间尺度的模型扩展到了统计模型[18]。
定义sloppy属性时,基于Hessian矩阵或Fisher信息矩阵值的判断是依赖于它所评价的参数空间的。当采用MCMC(Markov Chain Monte Carlo)后分布得到的多个参数集合进行计算时,尽管会得到相似的特征值谱但却有不同的特征值。由此可见,这种sloppy属性判定方法是基于局部特征,因此不够精确。主成分分析可用于对点空间中的协方差矩阵进行特征分解,第一主成分就是最大特征值对应的特征向量,对应着点变化量最大的方向且各成分间彼此正交。因此可以用主成分分析类比Hessian矩阵。通过使用主成分分析MCMC参数集合或中间参数集合[9],则可得到分析sloppy属性的全局视角。
2 Sloppy属性的起因及消除
由于参数估计遇到了困难,研究者们才将参数划分成了sloppy和stiff类型。因此对于sloppy属性的起源、本质及消除的探索一定是和参数估计联系在一起的。
2.1 从特征值谱角度探索起因
Waterfall小组基于“损失函数对称依赖于模型参数”这一强假设前提,探索sloppy属性的起因[19]。在此假设下将损失函数中的残差r写成参数多项式和的形式如式(7)所示。

(7)
再假定参数变化都被限定在一个微小的范围内pi∈[p±ε],可以得到εi=pi-p,则Jacobian矩阵可以改写为式(8)所示。
(8)

当K无穷大时,Hessian矩阵可以分解为H=JTJ=VTATAV,这里的V就是范德蒙矩阵。通过比较sloppy和非sloppy属性的范德蒙特征值发现,对于非sloppy模型来说,当ε →0时相邻参数的相对空间是宽度趋近于1的固定值。但真实世界中的sloppy模型并不总是满足此假设前提,由此可见,sloppy的产生是因为实验的封装或描述的需要扭曲了参数的自然属性而造成的,而这种扭曲则是为了达到描述复杂模型的目的。
同样是针对Hessian矩阵的特征值谱,Tnsing研究小组针对多领域中普遍采用的ODEs(ordinary differential equations)模型进行研究[20]。无需知道系统结构以及任何测量观察信息,他们使用随机矩阵理论分析协方差矩阵的结构发现,当敏感矩阵的平均特征值宽度达到0.985的时候,模型即可呈现出清晰的非sloppy属性。因此消除sloppy属性,本质就是控制Hessian矩阵特征值谱的宽度。具体可以采用的方法有:1)只选择有特色的数据点,以使敏感矩阵中变量之间的相关性变得简单,进而抑制sloppy属性的发生[21];2)选择最优实验方法或执行特定的实验扰动,使得敏感矩阵的水平方向结构收敛到每个参数自身,也会降低特征值谱的宽度,从而将sloppy属性减弱到最小。该研究小组从他们的研究结果出发,认为sloppy属性的出现只是实验设计引发的一种巧合,因此在不讨论实验设计的前提下就说某模型具有sloppy属性是不准确的。
2.2 实例检测发现起因
实验例证是寻找模型特性的一种常用方法,通过类比大量模型的共有特征,也可发现sloppy属性的起源。Gutenkunst小组从文献中抽取17个典型系统生物学模型,通过构建预测模型检测预测结果,总结出sloppy属性产生的原因如下[22]:1)参数空间中的裸参数和控制系统行为的特征参数之间存在着特殊的坐标变换关系,这可能是sloppy属性产生的最根本原因,因此可以通过实施坐标变换予以消除;2)sloppy属性和它要拟合的实验数据相关。如果实验数据不充分,属性间的耦合性会增强,造成模型的sloppy属性也会增强。此外在拟合具有时间序列特征的实验数据时,Tafintseva小组使用主成分分析法分析发现,sloppy属性和特定的非线性子空间结构之间有着特定的对应关系[23]。上述情况都可以通过增加实验的数据量,达到解耦待估参数之间的耦合性或消除此特定子结构的目的,进而达到消除sloppy属性的效果。很多非线性模型同时又具有多时间尺度特性,对这样的模型进行参数拟合时,变量的变化轨迹可以明显的区分为跳跃性变化的快片和缓慢变化的慢片,快片对应的是stiff属性方向,而慢片对应的是sloppy属性方向。通过将研究初始条件敏感度的李雅普诺夫指数(Lyapunov exponents)和Hessian矩阵做类比,发现李雅普诺夫指数空间既可以解释指数范围的sloppy参数空间,也可以解释具有相同尺度的非sloppy空间,因此在系统层面上将时间尺度和sloppy属性的敏感性建立了联系,进而认定多参数系统中出现sloppy属性可以归因于动态变化的多时间尺度属性。此时通过时间尺度切分即可消除sloppy属性。3)一些简单模型会因为不同参数组合的冗余性呈现出sloppy属性,这是因为研究者对系统理解的不够充分造成的,此时sloppy的消除可以通过获取先验知识加深对系统的理解予以消除。
2.3 信息几何角度认定起因
信息几何组合信息理论和差分几何理论来探索参数化的模型,通过更多地关注数据空间而不是参数空间来理解模型的属性,因此更能达到使用数字技术探索模型本质的目的。本质上来说,模型是从参数空间到数据空间的一种映射,因此可以将模型看做嵌入到数据空间的一个流形[9]。
从信息几何角度看待sloppy模型时发现,Hessian矩阵的特征值在某些情况下具有层次结构,即嵌入到数据空间D的模型流形M所对应的预测流形有边界,使得横断面的宽度呈现层次结构,所以整体形成了一个长而窄的超脊形结构[24]。而超脊结构的产生是因为实验者对其所研究系统的本质特性了解的不够深入,使得选择的参数化模型违背了数学规律造成的,这也是sloppy属性产生的原因。因此可以通过对模型进行重新参数化或通过修订实验、测量标准来降低sloppy属性的产生。
Quinn小组在前人工作的基础上,采用更一般的多项式方法探求超脊结构的成因[6]。假定有非线性模型连续依赖输入参数θ={θ1,θ2,…θk},由该模型产生的预测结果为yθ(t),假定有多项式基为{Φi}i=0,则预测结果可以表示为式(9)
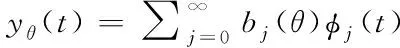
(9)
让P(θ)=(P0,…PN-1)定义模型的流形,其中
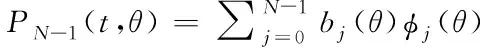
(10)
t是时间序列t={t0,…tN-1}T,则预测模型可以改写为
P(θ)=Xb
(11)
其中,Xij=Φij(ti-1),b=(b0(θ),…bN-1(θ))T,因此X构成了从参数空间到预测空间的线性映射。假定‖b‖2 使用数学模型描述真实系统时有如下两种选择:大而复杂模型可能和真实情况更接近,但因为参数众多会存在参数的不确定性,简单模型只抽取最本质构成,但模型本身会有不确定性。Sloppy模型是复杂模型,因此对该类模型进行参数估计时面临的最大挑战就是因为参数的不确定性而引发的病态问题(ill-condition)[25]。参数的病态源于对噪声数据的高敏感性,这种病态对模型而言是固有的但对数据却不是。因此一些研究者认为模型应该具有唯一性才能克服病态性[26]。还有些研究者认为在参数估计之前应该先认定冗余参数以避免病态模型或者错误的收敛过程[27]。 在实验数据有限的前提下要对复杂模型中的参数进行估计,有两种可行的方法:一种是通过实验设计产生出更多的数据;另一种是执行模型规约,在保留模型核心工作机制的前提下使得模型可以和提供的数据相匹配。实验设计就是决定对哪个组件实施扰动,以及在哪个时间点进行测量。其本质就是如何获取最大化信息,使用的方法可以是基于贝叶斯后取样[28],信息理论以及敏感分析[29]。而不同方法的区别在于如何定义最大化的信息,贝叶斯标准是最大化期望值,信息论的方法是利用熵和交互信息定义额外信息量,敏感度分析是希望找到最大化减小待估参数不确定性和方差的实验,常用的衡量实验好坏的标准就是A-optimality和D-optimality。而模型规约可以是基于时间尺度[30]、基于模块性、也可以是基于敏感性[31]。 这两种参数估计方法看似无关但实际上有很深的联系,使用模型流形和子集似然(profile likelihood)这个统一框架可以将二者联系起来[32]。从几何角度来讲,实验数据是数据空间中的一个点,数学模型是存在于数据空间的流形,参数估计是数据点到流形上的投影,通过检测投影点在流形投影附近的特征值,既可以执行实验设计也可以进行模型规约。实验设计认定新的实验点,因此可以扩展流形并且移走奇异点。而模型规约认定的是流形最近的边界,它是最近的特异点,所以是执行规约模型的最合适形式。 故此针对sloppy模型,进行参数估计的思路也可归结为这两大类,再加上对已有优化算法的改进,下面就从这三个方面进行介绍。 模型规约就是使用低精度模型代替原始复杂模型,但低精度模型保留了原始复杂模型的核心机制。模型规约广泛应用于航空、水文地质及石油钻采等多个领域。 从统计学集合角度解释来看,Sloppy模型中几个刚性参数的组合可以被理解为原始模型的低维有效模型,这自然引发了使用低维模型近似高维模型的模型规约问题。规约后的模型有利于发现系统行为的新兴控制机制,这种规约不同于为了避免参数过适应效果而讨论的模型简化。流形中超脊结构的存在使得模型流形边界具有层次结构,因此可以利用这种层次性来实现模型规约。Transtrum研究小组据此提出MBAM算法(Manifold Boundary Approximation Method)实现模型规约[33],该方法分为4步:1)基于Fisher信息矩阵解析认定最小敏感度参数组合;2)数值构建模型流形测地线认定流形边界;3)如果发现了流形的边界,则初始模型的近似模型得以认定 4)通过让近似模型拟合初始模型的行为来认定参数的值。Pare研究团队使用MBAM到系统的不同参数集合得到不一样的近似结果[34],说明模型规约也会产生不同的近似模型,而这些近似模型本质上是对应着一个流形的同一个边界,进而验证了模型流形是模型参数的一个特定选择结果且模型流形是嵌入到样例空间的。MBAM方法不仅被用于研究生物系统,还被用于探索微生物控制土壤时碳循环系统中的参数认定问题以及核能密度函数中sloppy模型的规约及函数的约减,以及电力系统模型的规约问题。 Sloppy模型除了具有超脊结构之外,还有一些呈现出多峰值结构,此时模型流形的适应能力比参数数目所表示的能力要大得多,同时也为参数拟合提出了更高的挑战。多峰值模型在参数估计时面临的主要问题是需要为了跳出局部最小值而增加搜索参数空间的范围,但很多常用的搜索算法因为只能找到一个局部最小值且不是全局最小值而对多峰值问题失效[35]。另外此类sloppy模型的高有效维度也反映出已有的度量标准不能精确捕获模型中感兴趣的信息。Francis研究小组针对这种高有效维度sloppy模型参数估计问题,从构建新的相似性标准开始,引入信号处理方法解决该问题[36]。具体做法是: 首先对参数进行敏感度分析;再根据参数的尺度行为对参数组合进行分类;对于Hessian特征值来说,不同的尺度行为对应着损失界面的不同结构及模流形,因此再根据最大特征值行为对模型进行分类。引入winding frequency和模型流形上的曲率来估计参数空间中局部最小值的密度,通过合适的选择距离度量尺度,模型流形不仅可以移除局部最小值而且保持距离的相对物理解释,更有助于认定复杂系统中的未知结构。 减少待估参数数目在一定程度上也有助于在有限的实验数据下提高参数估计的准确性,因此也是模型规约的一种。Tafintseva研究团队通过在不同初始条件下提供的大量实验数据集合,通过多轮拟合确认参数中的sloppy参数,以达到减少待估参数的目的[23]。Kardynska等基于sloppy/stiff参数敏感度分析方法创建参数阶排序,以此来找到重要的参数以降低需要精确估计的参数数目[17]。但使用Fisher信息矩阵计算的参数敏感性是基于局部信息的,它只有在测量不确定性特别小的前提下才有效果。同样是基于敏感度对参数在系统中的角色进行认定,Liu研究组针对噪声数据下很难直接对所有参数进行认定的问题,基于敏感度认定结果,采用三阶段策略实现对sloppy系统的参数估计[37]。首先采用一个比较粗糙且计算费用低的算法为sloppy参数初步指定参数值,其次采用更严格的取样接受标准来估计stiff参数值,最后在近似贝叶斯计算框架下使用自适应算法逐步缩减错误误差。针对测量的不确定性不可忽略的情况,Raman小组引入多尺度sloppy属性方法,将敏感性的各向异性定义为扰动长度尺度相对于固定数据集或模型预测的函数,从而为不可认定性检测问题提出了将参数空间的不可认定横截面作为优化控制问题的数值解决方法,为模型简化和参数约减提供支持[38]。此外还给出了似然率检测和多尺度sloppy之间的理论关系如式(12)所示,其中δ 是相对于θ带来的扰动θ*的长度尺度。 (12) 在贝叶斯统计分析里,先验一般是指参数空间的先验可能分布,该分布给出了随着参数变化时模型的可能密度信息。因为先验可以最大化参数和预测之间的交互信息,从有限的数据里学习最多的知识。因此先验不仅有助于在模型选择时找到最有效低维模型,而且在参数识别过程中更有助于得到更快的收敛速度以及更小的认定错误[39]。同时先验信息还可以阻止优化过程中参数组合引发的参数蒸发问题[24]。 Transtrum组通过将参数拟合问题看做插值过程,从差分几何角度分析sloppy参数估计过程发现,基于最小平方损失函数进行数据拟合的困难主要源于模型流形的层次边界中存在很窄的边界。当参数拟合执行到这些窄边界时,优化收敛过程变得缓慢,外在表现就是sloppy参数值变化很大但损失函数却变化很小。为了克服窄边界的局限性,研究者引入参数空间图来构建模型图,既可以移除流形图的边界问题也可以克服参数空间图移动不连续问题,同时也提供了一种解释数据空间和参数空间自然方向的方法。通常使用下列式(13)定义模型图。 (13) 其中第一部分是模型流形的度量,第二部分是参数空间的度量。当模型图无效的时候,可以引入先验。为每个参数增加两个先验,如式(14)示[24]。 (14) 前者用来惩罚大值,后者用来惩罚小值。增加先验后,模型图修订为式(15)所示。 (15) Mikhail研究小组发现已有的实验先验信息在点估计时并不能提高参数的估计效果,究其原因是因为数据内容提供的信息量过少[40]。据此他们提出基于组合实际数据和人工生成数据共同作为实验先验的全贝叶斯变体方法,以达到限制参数分布的目的。全贝叶斯实验先验方法是之前实验先验点估计的直接扩展,直接拟合池化后的每层后验分布,该扩展使得参数估计不确定性可以直接反映在实验先验中。由于每个变量都对应多个数据点,使得以组合方式估计多变量部件中的每一个变量的协方差成为可能。但该方法并没有在参数估计时表现出更明显的优势,因此研究者们建议应该把目标转向到如何获取或提升实验获得的量方面 L-M(Levenberg-Marquardt)算法被广泛应用于非线性函数的参数估计问题。该方法主要用来处理Jacobian矩阵秩的亏损,同时也为高斯牛顿算法提供了一个全局的策略[41]。将置信区间方法应用到高斯-牛顿算法中用于近似Hessian矩阵,即可基于式(4)得到L-M迭代更新参数公式为式(16)。 δθ=-(JTJ+λDTD)-1g (16) 其中λ是拉格朗日乘子用来控制步长的边界,而g=JTr是梯度。如果λ和步长选择的合适,甚至可以达到全局收敛的效果。 L-M算法有很多优点,比如在原子能模拟领域,通过将L-M算法合并到常用的potfit方法里,将其作为求解局部最小值的最新算法,使得构建出来的原子间势能更拟合sloppy模型。但多数情况下,如果将L-M直接应用于sloppy模型的参数估计有很大困难,因为超脊结构下参数估计会面临在平坦宽阔区域参数消失、在狭窄寻优区域进展缓慢、以及优化结果对初始值依赖程度大等问题[42]。Transtrum小组对标准L-M算法从三个角度进行修订以克服上述困难[42]。1)在假定模型图形的外曲率非常小的情况下,对残基引入泰勒近似的二阶项来调节L-M算法的步长,以帮助L-M算法对初始条件保持鲁棒性,使得在降低计算Jacobian矩阵耗费的情况下能以很高的成功率找到最优值;2)针对狭窄区域搜索缓慢但却很少发散的特征,适度接受上坡的移动可能有助于加快寻优的进程;3)因为每轮迭代都需要重新计算Jacobian矩阵,以往的研究者们采用不同的方法减轻此计算负担,如使用Jacobian矩阵的主子矩阵,对Jacobian分区切块处理,同时扰动Jacobian矩阵。Transtrum研究小组则采用拟牛顿根发现方法替代Jacobian矩阵的每轮计算,公式如式(17)所示,只在1-2次拒绝接受步长后再重新启动计算过程,也可以节省计算时间。 (17) Transtrum小组在L-M残基中引入高阶项之后,又提出将高阶项作为测地线加速的方法[43]。通过差分几何导出测地线加速项,这里的测地线加速并没有试图提高高斯-牛顿近似的Hessian矩阵,而是将小残基近似扩展到了立方阶。在导出测地线加速时,小残基近似被小曲率近似替代,后者为高斯牛顿近似和L-M算法提供了更宽广的调整空间。即使最好拟合时残基特别大也可以调整,因为这是模型的属性而不是数据适应的属性,这个思想贯穿到算法的整个阶段而不只是在最优值附近。为了节省计算负担,该算法还将测地线加速中需要计算的二阶导数替换为二阶方向导数,只需对残基进行一次评价计算即可完成。 Brunel小组研究发现[44],L-M在寻找最优参数时敏感矩阵扮演了至关重要的角色。即使在提供大量实验数据的前提下,如果参数θ在状态Xθ是稀疏取样,也会对拟合结果造成很大的偏差。因此特异敏感矩阵的存在是参数估计反问题成为不适定性问题的元凶。据此,针对ODE模型,该研究小组基于广义光滑算法[45]定义了一个两步程序,通过改写ODE方程为其近似形式如式(18)。 (18) 再通过使用被残基u(t)控制的ODE的轨迹Xθ,u达到规避求解Fisher矩阵,明确控制估计的近似偏差,以及获得偏差测量的目的。 参数估计又称参数可认定性,是指从一个已知系统的实验及信息中获得所有未知参数值的能力[27]。可认定性分为结构可认定性与实际可认定性[46],结构可认定性是指从实验数据得到的参数值具有唯一性,实际可认定性是指参数估计值的置信区间具有有限尺寸。一个参数在结构可认定基础上,仍然可能是实际不可认定的,这归因于两个点,一是所提供实验数据的质和量不够充分,二是由于测量时间点的选取不合适。此时,尽管有时似然估计目标值对这个参数具有最小值,但置信区间却无限大,因此估计得到的参数值变得没有意义。当参数之间有补偿效果的时候,通过以和的方式作为目标函数来认定模型中的每一个参数是困难的[16]。 参数估计值的不确定性是指以多大的可信度确认参数值的准确性,参数估计的结果当然是希望不确定性越小越好。但参数估计的不确定性受到模型的复杂度、数据的充分性、数据的噪声以及sloppy属性等诸多因素的影响[21]。降低参数估计不确定性的方法主要集中在对数据集的处理,如通过不断对调控参数的数据增加扰动[13],使得一个数据集中参数不确定性大的方向对应另一个数据集中参数不确定性小的方向,即让不同的数据集之间具有互补效果[16,19],或者进一步探索实验不确定性和实验条件之间的关系。 模型中的未知参数需要基于实验中观察到的数据进行估计,但相对于模型的复杂性而言,当实验提供的数据数目有限的情况下可能不足以限制住参数[47]。因此截然不同的数据集可能会产生相同拟合效果的参数集[23],这就是模型复杂性和数据之间信息差异的显现。那么是否提供足够多的实验数据,就可以认定模型中的sloppy参数?实验设计对参数估计有什么样的影响?不同学者从不同的角度进行了探索。 一些研究者发现,sloppy属性和“结构不可认定”之间不存在等价关系[5,14]。通过增加实验数据的确可以提高参数估计的精确性[12],而且在sloppy区域的误差也很小,在可提供噪声自由的实验数据条件下,有可能为待估参数找到唯一的值,但基于此模型的预测结果和实际实验结果偏差却很大。该情况说明在模型构建时细节没有考虑清楚的条件下,为了估计出参数需要不断补充实验数据,使得之前模型中不相关的部分变得相关同时也引入了系统错误。因此,与其一味地增加实验数据提高参数的可估计性,不如在参数估计前先确定哪些参数和模型的运行机制密切相关,再做参数认定能更有效。从这点来看,实验数据的增加应该让位于模型规约以及参数化简。再有,因为sloppy属性和模型结构之间的关系还不能完全被研究者掌握,因此依据一定的可信度计算出待估参数的值比唯一认定参数值更具有现实意义。 实验方案的选择同样对参数估计结果有影响,研究者们提出了很多实验方案的改进方法以有利于参数估计[48]。Chis研究小组发现在不同的实验实现条件下,sloppy参数的估计值不同[5,14],针对不同的最优实验标准,相对置信区间的分布也不同。因此对所有参数而言提高认定比例在某种程度上一定会使置信区间降低,但sloppy属性仍会保持不变,因此实验设计应该使用E-优化[49]或D-优化[50]而不是追求sloppy最小化。限制实验中的噪声可能会将sloppy模型转换为非sloppy模型,但并不意味着参数的可靠性估计不能被计算。而且经过精心选择取样时间对于sloppy属性消除的效果好于单纯增加实验数目的效果。Apgar和Chachra小组则发现,当实验数据通过不同方式产生时,所有数据均能以较高的精确度对参数进行认定(真实值的10%范围内),也就是实验方法的多样性更有助于参数认证[13]。因为此时不同数据集合之间是互补关系,每个集合都包含了其他集合成员不能提供的信息,此时一个实验大的不确定性方向对应着至少其他一个实验的小确定方向,因此就数据整体来说所有的信息都是充分的。 Transtrum小组还针对参数估计问题给出了实验选择算法[51]。他们首先定义参数估计精度的公式如下式(19)所示: (19) 据此提出对参数拟合而言的实验应通过如下步骤得到: 1)找到提供的所有数据中,参数拟合最好地那组数据;2)假定1)中得到的参数就是参数的真实值,据此对所有其它数据再次执行拟合过程;3)根据参数估计精度公式对潜在的实验重新进行评价;4)对每个实验找到降低拟合错误的方法;5)不断增加新数据重复实验直到估计错误足够小时停止。 构建数学模型一方面是研究系统的工作机理,另一方面就是对系统未来的行为进行预测,因此参数估计结果的好坏也影响着模型预测的准确性[13]。即使模型中的每个参数只有一个适度的错误,都会导致预测结果在一个很宽的范围[52]。当一个模型中包含很多参数,即使每个参数都只有很少的精确性,只要在模型预测时把这些不精确性的相关性考虑进去,也能产生有用的预测[16]。集合性适应一定数量的数据可以严格的限制模型的行为但却无法限制参数的组合效果,此时在没有关于每个参数的精确值时,可能会做出低确定性的预测,因此精确的参数值对于可靠性预测而言至关重要[21]。 并不是所有的参数对该预测都重要,因此如果一个模型在某个特定预测时只和某些参数组合相关,则参数认定时只认定这些参数即可[13]。而且实际情况是,sloppy模型下的参数估计都有不确定性,那么参数值的变化能在多大程度上影响预测的结果,这就需要一种能评价预测能力的评价方法。参数敏感度分析研究的是参数值的变化对模型输出的影响程度[53],因此评价预测效果的方法一定和敏感度分析息息相关。还有的研究人员通过定义相对刚性敏感度和相对敏感度如式(20-21)所示来探索此问题[54]。 (20) 其中 (21) s=J′JW是常数 当预测模型比拟合模型更敏感时RSS可能会提供更多信息,而RS通常适用于参数只负责预测情况的场合。当这两个相对测量值趋近于0时,表明参数估计是从非常低精确率的拟合中得来的,因此不足以给出有效的预测。 为了考虑参数间的相关性这种模型不确定性的来源,他们又定义了相关性测量公式如式(22)所示。同样,趋近于0的RCM表明参数认定效果差会影响预测的精确性。 (22) 模型的过度参数化会导致基于模型的预测性能的退化,因为预测性能依赖于模型参数的精确估计而每个参数的不确定性叠加又会造成预测性能的降低[55]。因此,一开始建模时就面临这样一个两难的选择:是选择增加参数的数目提高数据拟合的效果还是减小参数数目以提高模型预测的效果?在考虑这两点因素情况下的预测性能优化通常可以使用AIC(Akaike information criterion)[56]或BIC(Bayesian information criterion)[57]最小化进行度量。但这些标准在很多应用中失效,失效的根本原因无非是参数的不确定性以及模型的多峰值性[58],而这两个特性对sloppy模型来说都存在。当Sloppy模型中存在参数的不确定性时,此时AIC会高估真实情况的复杂性,如果sloppy模型有多峰值时,AIC又会低估真实系统的复杂性。针对此情况Lamont小组提出一个新的模型选择标准FIC[59]: FIC(X,Μ)≡h(X|X)+R (23) 其中h的负无偏定义及R定义为 (24) 该标准是AIC的更一般形式,不仅在数据量有限时效果优于AIC,而且不受ad hoc先验分布和正则的影响,因此特别适用于贝叶斯模型的选择,即使模型没有解析表达式提供的情况下,计算效率也有优势。 近20年间,数学模型Sloppy属性的特征、起因、与模型其它属性的关系及由此引发的参数估计及模型预测问题得到了广大研究者的广泛关注和深入研究。这些研究的发展及取得的研究成果使得人们在面对sloppy模型属性时有可以借鉴的理论依据及有效的解决方法。在本文中,基于所能接触到的文献对sloppy属性的相关工作进行了综述总结,从分析sloppy属性在各类数学模型中的普遍性及广泛用途,到判断该属性的方法,以及从不同角度分析该属性产生的起因及消除,然后针对具有该属性特征的模型如何进行有效的参数估计都做了总结。基于以上的综述,针对该问题提出一些研究主题,以便持续推进该领域的未来发展。 1) 针对sloppy属性估计的特定优化算法研究 前述讨论优化算法的目标函数多采用点估计的最小平方和形式,对已有算法的改进也是从如何让最小平方和形式更有效的角度出发的。对于参数之间具有补偿效果的情形而言,和形式作为目标函数并不是一个很好的选择。那么针对sloppy参数估计而言,什么样的目标函数才是一个好的目标函数却几乎没有文献予以讨论。有效低维和有效高维有何判定特征,以及如何针对不同特征设计高效的参数估计算法也是未来值得探讨的问题。 2) sloppy属性全局评判标准研究 研究者们都意识到基于Hessian矩阵或Fisher矩阵认定sloppy属性是和特定数据相关的,因此是一种局域性的判定标准。尽管有研究指出可以使用主成分分析多数据集以获得全局视角,但分析多少数据集是足够的?是否有可以脱离数据集而存在的全局视角也是未来深入探讨的问题之一。 3) 保障模型预测精确性的参数估计标准定义 模型规约及增加实验数据都可以提高参数估计的精确性,但精确到什么程度的参数估计可以保证使用该模型预测的结果也是精确的,二者之间的定量关系怎样,目前研究涉及到的很少。 4) 一体化参数估计及模型预测的框架研究 模型构建以及基于模型进行预测是基于模型研究真实系统的两个不同阶段,二者相辅相成。但目前的认知通常把二者截然分开,且认为构建好的模型在预测过程中不应改变。这也是造成拟合好的模型预测效果差的原因之一。应该从一体化的角度构建这两个阶段的模型调控框架,让彼此之间有反馈和链接才能更好提升模型的预测效果。这样两个阶段的模型都是可以动态调整的, 5) 人工合成数据对参数估计及预测的影响研究 实验条件的限制造成能获取到的实验数据就那么多,有时因为成本的原因,甚至最优实验设计也未必能实施。因此使用人工合成数据提高参数估计和模型预测的准确率就变得尤为重要,但人工方式合成的实验数据对参数估计和模型预测是否有影响以及有怎样的影响,这方面的研究几乎没有涉及,因此也是未来的研究方向之一。3 Sloppy模型的参数估计
3.1 模型规约
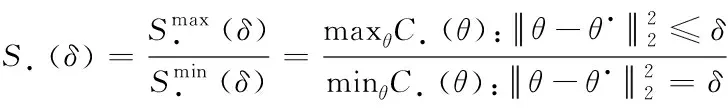
3.2 借助先验信息
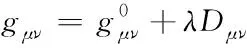
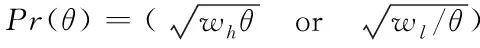

3.3 改进优化算法

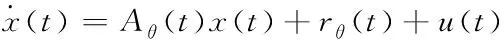
4 参数估计相关问题
4.1 可认定性与不确定性的影响
4.2 实验数据与实验设计的影响

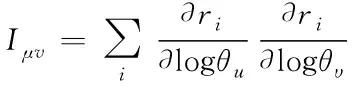
4.3 对模型预测的影响
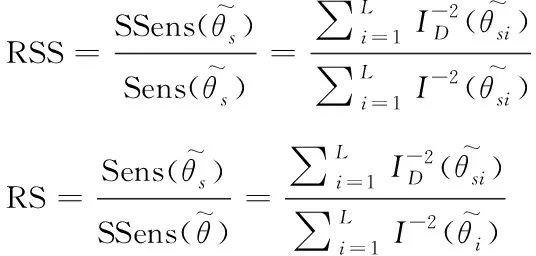

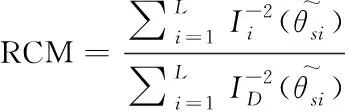
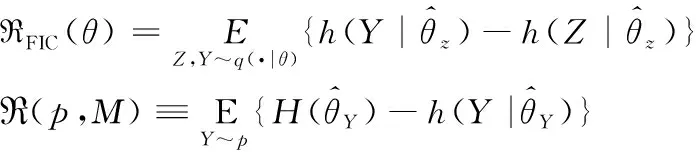
5 总结及未来研究方向展望
