结构化学材让学习趋向“整体”
2023-03-28左小平
左小平




摘要:强调课程内容结构化,就是要通过结构化实现知识的整体建构。数学知识比较抽象,结构化学材能够避免知识的分散、割裂现象,促进知识的整体感知、有效理解,因而成为学生学习的有益支架。结构化学材,让学习内容趋于整体系统,让学习过程实现整体关联。
关键词:小学数学;结构化学材;整体系统;整体关联
*本文系江苏省基础教育内涵发展项目“小学数学结构化学习课程基地建设”的阶段性研究成果。
《义务教育数学课程标准(2022年版)》(以下简称“新课标”)强调的课程内容结构化,就是要通过结构化实现知识的整体建构,从而便于发现知识的意义和价值。数学知识比较抽象,结构化学材能够避免知识的分散、割裂现象,促进知识的整体感知、有效理解,因而成为学生学习的有益支架。结构化学材,让学习内容趋于整体系统,让学习过程实现整体关联。下面,结合《小数的初步认识》一课教学具体阐述。
一、结构化学材让学习内容趋于整体系统
结构化学材有着清晰的知识脉络结构,能够帮助学生在知识的整体与局部、本质与现象的联系中掌握知识。学生在使用学材的过程中,不断经历知识内化、凝聚的建构过程,不断理解、把握知识的系统性。
“小数的初步认识”是“数的认识”这一核心板块的重要内容。教学时,可以站在“数的认识”的高度设计学材,突出学习内容的系统性。通过“你知道0.3表示什么意思吗?选择1—2个学材表示0.3的意思,并用简短的语言记录下来”的大任务驱动,学生不断地建构“小数”的整体概念。
课堂中,为学生提供一组结构化学材:1米长的线段和1元的硬币,对接学生的生活经验,这是形象的学材,带领学生由生活体验进入数学学习;一个长方形,对接学生的学习经验,这是半抽象的学材,有效地引导学生由感知到想象,再到抽象;一处空白,让学生自创学材,这是一个开放的、抽象的学材,体现学生对生活问题数学化的理解,激发学生自我的数学对话。
涉及结构化学材的理解与应用包含三个步骤:
首先,展示不同的学材。先呈现“1米的线段”,学生对长度单位已有相当丰富的经验,能够根据1米等于10分米,联想到把1米平均分成10份,其中的3份就是0.3。再呈现“1元的硬币”(如图1所示),学生根据生活经验,用“1元等于10角,0.3元就是其中的3角”来表达自己对0.3的理解。最后呈现“一个长方形”(如图2所示),有的学生将长方形平均分成3份,认为其中的1份就是0.3。在交流中,引导学生发现,平均分成10
份,其中的3份是0.3。进而,让学生明白为什么要将这些学材分一分,即“0.3是小于1的数”,并在操作中自然体会到小数与整数的联系。
其次,展示学生创造的学材。学生的经验是创造的源泉,教师要对接小数的意义理解,促地学生对经验的“重构”。课堂中,有学生创造了“圆形比萨”(如图3所示),将一个比萨平均分成10份,表示其中的3份就是0.3。此外,有学生创造“正方形”,有学生创造“一个西瓜”,等等。多样的学材丰富了学生对0.3的理解。
最后,在对比中初步建构0.3的意义。一是通过“为什么这些不同的学材都能表示0.3?这些0.3又有什么不同?”的讨论,让学生实现对小数意义一般化的理解,即系统地理解“将一个物体平均分成10份,表示其中的3份就可以表示0.3”,而具体情境中“0.3”的意义却是不同的。二是关联旧知,引导“像这样的描述,以前我们用哪个数来表示”,拓展小数一般化理解的应用。这样,促进了学生对小数是十进分数的“一致性”理解。而“做”的经历,对小数的模型建构起到了重要作用。
知识存在于“整体—部分—整体”之中,“部分”的知识深深地嵌于“整体”的学习之中。上述结构化学材,有坡度、有广度、有深度,让学生从整数“1”到分数“110”再到小数“0.1”,看到了不同形式数的内在联系,构筑起整数、十进分数、小数之间的本质关联,让学生从“数的认识”的整体角度理解小数。
二、结构化学材让学习过程实现整体关联
结构是系统的属性,是元素及关系的整体关联。结构化学材作用于学生主体,促进学生对知识元素及元素之间关系的理解,让学习过程变得整体关联,并促使学生实现对认知的自主建构。[1]
《小数的初步认识》一课,学生创造的學材(如图4所示)就是为了产生“0.3”的表象。教师要以学材为载体,将学生对小数的认知纳入数的体系中,以此丰富学生学习小数的过程,实现学习过程的整体关联。这个特殊的计数器关乎的是数位、计数单位、十进制等,联系的是小数与整数,使它们成为一个整体。这样的结构化学材,依据小数核心元素之间的关联,创造真实的学习情境,促进认识小数的过程实现由内而外结构化的理解。
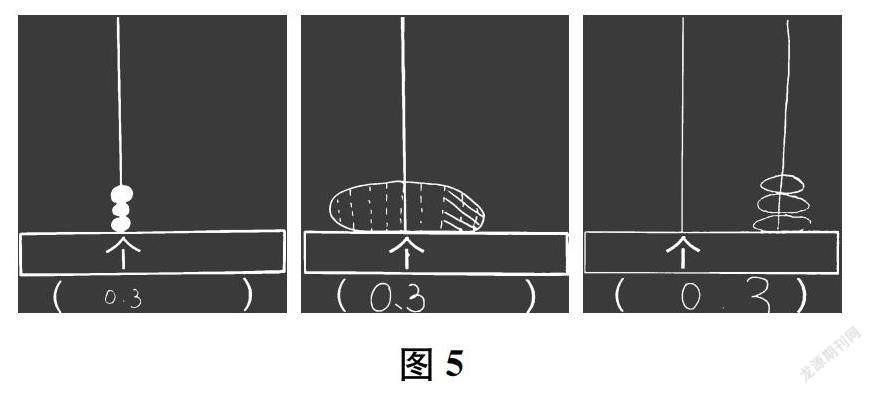
通过“你能尝试在计数器上表示出0.3吗?”这一问题,引发认知冲突,引导学生创造“小数”。计数器上只有个位没有小数,教师通过呈现学生的三类代表作品(如图5所示),引导学生分类辨别正误。对于第一幅作品,学生凭借已有经验直接给出判断。对于第二幅作品,学生借助此前利用不同学材表示0.3的经验,自然联想到在计数器个位上画一颗珠子就表示1,把这颗珠子平均分成10份,然后取其中的3份,就是0.3。而有学生认为,在计数器上无法将1颗珠子平均分成10份,于是创造了一个数位,即在个位的右边画一个“竖杆”来表示,得到第三幅作品。他们是这样理解的:“个位上肯定是0,在它右边画一个竖杆,0.3就在个位后面的数位上画3颗珠子。”学生在对不同作品的思辨中将数与数位结合起来思考,使每一个数在计数器上都能找到表示的方法,实现了对小数的深入认识。
学生在尝试中创造出了新的计数器。三类代表作品的解读层层递进,无不关联到“小数”这一概念的核心元素。学生创造的这个数位是什么并不重要,重要的是学生从内心认可了十进制。计数器中的自由表达,将学生初步感受小数的数位、计数单位、十进制这些元素的过程,与整数的数位、计数单位、十进制之间的联系实现了整体关联,从而真正意义上将小数纳入整数的学习体系,体现“数的认识”体系的不断发展与完善,促进学生学习的正迁移。
参考文献:
[1] 吴玉国.小学数学结构化学习的实践研究[M].南京:江苏凤凰教育出版社,2021:1.
