基于自适应扩展卡尔曼滤波算法的道路纵向坡度估计

符 凯

（长安大学 汽车学院，陕西 西安 710064）

道路纵向坡度定义为海拔高度关于水平距离的变化率，以百分数表示，上坡为正值，下坡为负值[1]。道路纵向坡度会影响汽车行驶过程的能量变化，纵向坡度较大时，在上坡路段，车辆容易出现熄火现象，在下坡路段，由于重力的影响，车辆会加速行驶，反复使用制动器容易出现热衰退现象，导致刹车失灵，增加驾驶员的操作难度，易引发交通事故，获取实时的道路纵向坡度可以使车辆更加高效和安全地运行[2]。

本文主要是针对道路纵向坡度的研究，主要是通过轮胎纵向力和车速来估计坡度大小，但因为获取的参数存在未知的噪声干扰，采用自适应扩展卡尔曼滤波（Adaptive Extended Kalman Filter,AEKF）算法来过滤噪声[3]，在 MATLAB软件下的Simulink中建立仿真模型，设置工况来验证模型准确性和实时性。

1 坡道识别原理

当汽车在坡道上行驶时，受到的力有坡度阻力Fi，驱动力Ft，滚动阻力Ff、空气阻力Fw和加速阻力Fj，纵向受力分析如图1所示。

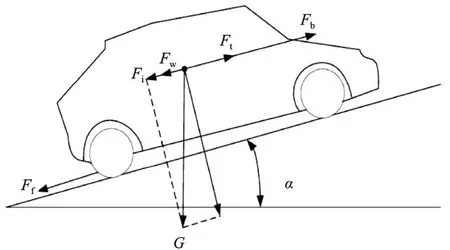
图1 汽车纵向受力分析

汽车纵向平衡方程为

将G=mg、Fj-˙、Fi=mgsinα带入式（1），并将取δ=1可得加速度公式：

式中，v为车辆纵向车速，m/s；m为整车质量，kg；Fmid为等效在车轮中心的轮胎纵向力，N；α为道路纵向坡度角，°；α上坡时取正号，下坡时取负号；G为汽车所受重力，N；g为重力加速度，m/s2，取 9.8 m/s2。

进一步推导式（2），可以得到关于坡度角的方程式为

式中，Fmid和v都可以通过传感器获取[4]，Fw可以通过计算获得，所以当已知汽车质量m时，能够求解出道路坡度角的正弦值。结合实际情况分析，公路设计标准中道路的纵向坡度不能大于9%，及对应的角度则是在 5°以内，因为角度小，可以认为坡度角的正弦值和正切值相等。

2 基于卡尔曼滤波算法的道路纵向坡度估计

2.1 建立非线性状态空间模型

本文是利用测得车轴端力传感器数据和汽车控制器局域网（Controller Area Network, CAN）总线上获取的实时车速来估测道路纵向坡度，但因为观测器产生的噪声会影响计算数值的准确性，因此，用自适应扩展卡尔曼滤波算法过滤产生的噪声，降低噪声影响。

基于卡尔曼滤波算法建立非线性状态空间模型[5]：

式中，X(t)为系统状态量；U(t)为系统控制量，因为Fmid是观测驱动力、制动阻力和滚动阻力的合力，包含U(t)，所以此时U(t)=0。结合式（3）将式（4）展开：

式中，A为迎风面积；CD为空气阻力系数；ρ为空气密度。将Δt为间隔，使用欧拉算法将系统状态空间转移模型离散化用以实现递归运算：

上式中系统状态转移矩阵为

观测矩阵为

噪声向量为

观测噪声向量为

通过式（6）—式（10）获得的参数可以求解道路纵向坡度。

2.2 噪声方差估计

假设w为系统噪声；n为观测噪声，两者均是满足方差一定、均值为零的高斯白噪声，服从条件：

Q和R代表白噪声的方差，Q和R取值会影响卡尔曼增益。可以影响Q的因素有模型误差、舍入误差、离散化误差和控制量误差。参数R的取值决定于传感器特性。采用自适应扩展卡尔曼滤波器对道路纵向坡度进行估计，能在不影响准确性的前提下，确保滤波器更快的收敛，但需要反馈来实现递推过程。在每个时间步上，都需要时序更新和观测更新。

时序更新：

式中，为估计中间量；为观测中间量；P为状态向量误差协方差；θ为衰减因子；s(k-1)和X(k-1)变化有关，呈正相关性。

观测更新：

式中，e为观测误差；E为单位矩阵；时状态向量误差协方差中间量。

通过最大似然原则的方法，得到系统噪声协方差Q和观测噪声协方差R，如下：

式中，N为利用过去时刻的数量；G为观测向量误差方差。

2.3 滤波器工作流程

矩阵P是一个3×3的对角矩阵，当对角线上的元素越大时，系统状态向量Xˆ(k)估计的置信度越小。在开始试验时需要采集较大的数值。滤波器可以在选取完参数Xˆ(k)和P后，从初始状态进行实时更新，实现道路纵向坡度的估计。

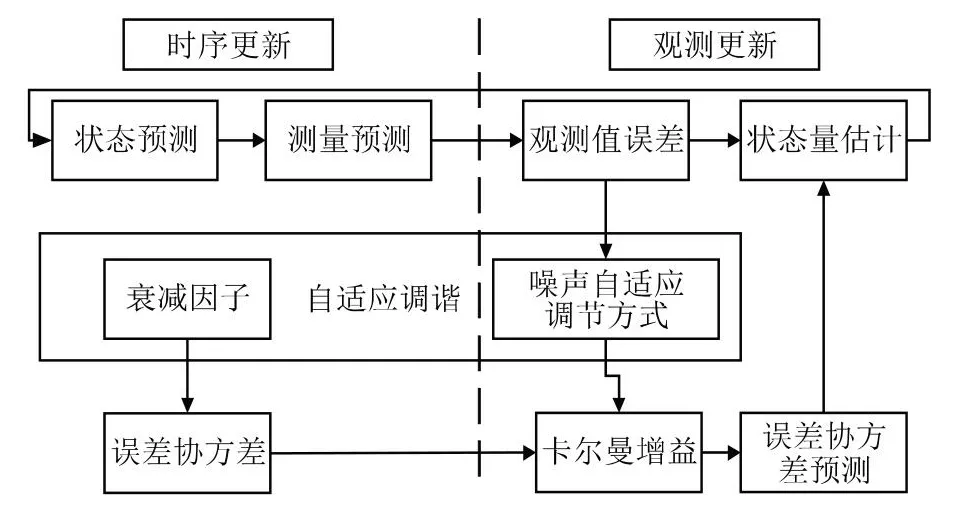
图2 自适应扩展卡尔曼滤波器工作过程

3 仿真过程

3.1 道路纵向坡度仿真模型

在Simulink中搭建仿真模型，建立典型道路模型，车辆参数在力传感器和CAN总线处获取，代入道路坡度仿真模型，用仿真的结果和设计的坡度进行对比，来确定此道路坡度估计方法的准确性和实时性。

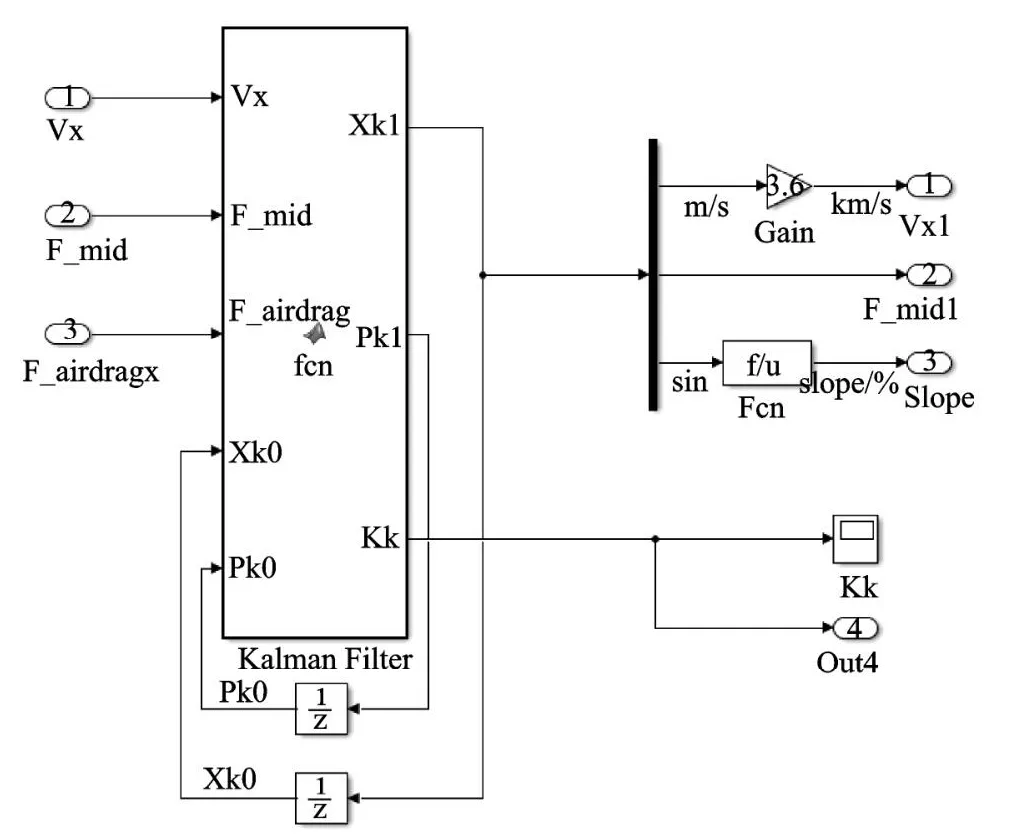
图3 Simulink道路纵向坡度估计模型

依据《公路工程技术JT J001—1997标准》中的公路设计规范如表1所示[6]。

表1 各级公路参数表

本文不考虑弯道情况，设置仿真道路总长为4 km的直线道路，道路纵向坡度变化周期为0.2 km，路面超高为 0，附着系数为 0.85的沥青混凝土路面，初始车速72 km/h。

如图4所示，在变化坡度上自适应卡尔曼滤波器可以根据当前状态不断调整估计值，所预测出的道路纵向坡度和所设计的坡度偏差在0.2%之内，根据设计车速，完成估计值的整个过程车辆前进行程不超过0.05 km。综上仿真结果表明，所提出的道路纵向坡度估计方法能够对突变道路的纵坡进行稳定的估计和预测，并且具有较高的准确性和实时性。

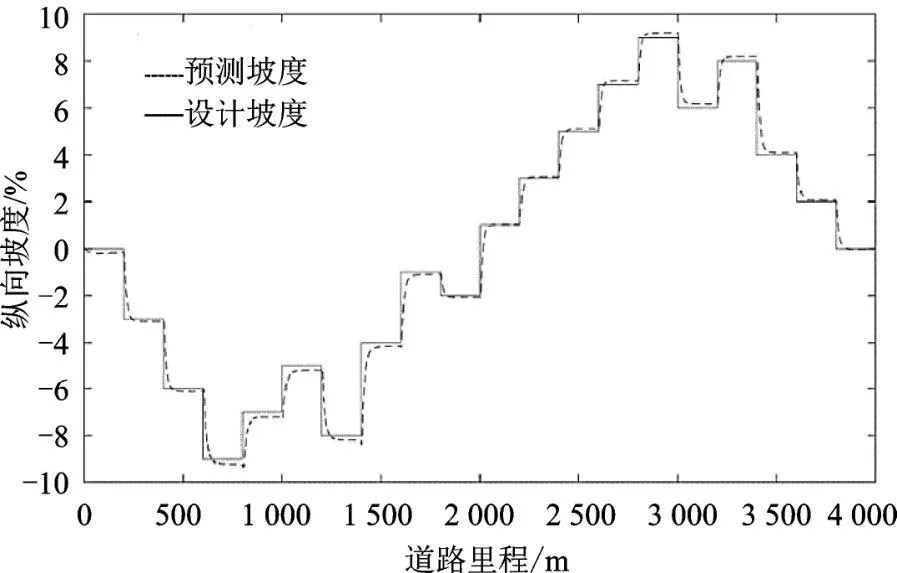
图4 道路纵向坡度仿真估计结果

4 结论

本文结合车辆在道路上行驶时，装配的力传感器和CAN总线获取的数据，运用自适应扩展卡尔曼滤波算法来实时估计道路的纵向坡度，可以有效地降低预测过程中产生的误差，优化预测结果，达到了实时、准确预测道路纵向坡度的目的，可以用于商用车或者智能车的路径规划问题，优化车辆在坡道路段行驶的能力。