基于融合学习的无监督多维时间序列异常检测

周小晖 王意洁 徐鸿祚 刘铭宇

（并行与分布处理国家重点实验室（国防科技大学）长沙 410073）

（国防科技大学计算机学院 长沙 410073）

随着云计算技术的不断发展，越来越多的用户利用云服务开展业务，并且随着多云时代的到来，用户更倾向于将应用和数据放在多个云平台上进行管理而不是锁定在一个云平台上.然而目前不同云平台提供的云服务之间并不相通，无法满足用户对于多云服务的需求.在云服务实体发展的趋势下，云际计算作为一种新型云服务模式，能够对多方云资源进行深度融合并统一提供云服务[1].然而目前云际计算技术尚处于发展阶段，多云之间的数据异常复杂，如何构建可靠的云际计算环境成为当下一个重要的研究课题.云际智能运维作为维护云际计算环境的关键手段，目前正处于研究发展阶段，它包括了故障分析、数据预测、异常检测等诸多研究领域.其中多维时间序列异常检测能够对多云交互间的复杂时序数据进行检测并对异常数据点产生告警，是云际智能运维的重要研究领域之一.异常检测已经在众多领域（图像、音频、时间序列等）得到了广泛的研究[2]，目的是挖掘出在同一数据集下那些和其他观测值有很大偏差的观测实例，这种偏差可能由很多因素引起，偏差的形式也各不相同.在过去，通过领域专家对各个监测指标进行静态阈值设置并对那些超出阈值的数据进行异常故障报告对于一个系统的容错性和健壮性至关重要[3-4].但是随着近年来云计算的不断发展，时序运维数据呈现出爆炸式增长，数据规模和数据复杂程度都在不断扩张，单靠人为地异常规则定义和异常报告并不足以完全对数据进行异常检测，而且这一过程也会耗费大量人力成本[5-7].随着大数据分析技术和深度学习技术的不断发展，越来越多的研究人员开始尝试用智能异常检测取代人工异常检测，许多针对时间序列的异常检测算法不断涌现，用以帮助专家处理越来越多的监测数据[8-9].然而由于云系统的复杂性，不同指标之间存在关联性（例如CPU 温度和CPU 的吞吐量呈正相关），简单对每个单维度时间序列进行单维时间序列异常检测无法捕获不同维度之间的关联性.因此在复杂云系统中，相较于简单的单维时间序列异常检测，运维人员更倾向于使用多维时间序列异常检测方法对系统的整体状态进行检测[10-12].

由于在云际智能运维场景下时序运维数据存在数据规模大、流动性强等特点，并且异常发生是小概率事件，因此想要获取带有异常标签的数据极其困难并且十分耗费人力以及时间.相较于需要训练集带有标签的有监督异常检测方法以及半监督异常检测方法，无监督学习更加适用于多维时间序列异常检测的应用场景[13-14].出于异常标签难以获取的实际情况，本文提出的是一种无监督的异常检测方法.在无监督多维时间序列异常检测领域，大致可以将异常检测方法分为基于重构的异常检测方法以及基于预测的异常检测方法.基于重构的异常检测方法是通过从正常时序数据中学习嵌入表示，对时序数据的正常模式进行重构，重构误差越大表明越可能存在异常.然而现有的基于重构的异常检测方法要么是缺乏对指标度量间的关系挖掘[10,15]，要么是无法学习到时序数据的有效嵌入表示，对于时间序列数据的时间依赖性建模能力差[16-17].基于预测的异常检测方法[18-19]是根据正常时序数据的历史数据对当前时间点的指标进行预测，当预测的指标值和实际的指标值有较大偏差时就表明该时间点存在异常.但是在复杂的实际系统中，有些指标数据就是固有的不可预测[10]，无法通过有效的方法对这些指标进行预测，因此采用预测误差对多维时间序列进行异常检测可能会产生较高的误报率.

基于以上观察，对于多维时间序列异常检测，本文的核心思想是对多维时间序列的数据局部特征和数据全局特征进行建模，以更好地捕获多维时间序列的正常模式，但这一思想面临2 个主要挑战：首先，独立学习数据局部特征和数据全局特征会使得特征融合变得困难，无法达到丰富特征信息的效果；其次，现实数据存在的潜在异常可能会导致模型存在过拟合风险.为了解决这2 个挑战，本文提出的基于融合学习的无监督多维时间序列异常检测（fusion learning based unsupervised anomaly detection for multidimensional time series，FLAD）方法通过在时域卷积网络中引入自注意力机制，在构建多维时间序列局部关联性的同时更加关注全局特征，并且加入信息共享机制对数据局部特征和数据全局特征进行融合学习，从而构建更加丰富的重构信息，最后通过重构误差检测异常.并且由于多层信息交互式网络结构的设计，特征信息间的不断丰富融合增强了模型的鲁棒性，有助于防止潜在异常导致的模型过拟合.

本文的主要贡献有3 个方面：

1）提出了一种无监督多维时间序列异常检测框架，通过挖掘正常多维时间序列信息的不同特征关联，实现多维时间序列的有效异常检测.

2）提出了一种基于融合学习的无监督多维时间序列异常检测方法FLAD，通过引入自注意力机制构建正常多维时间序列全局关联和局部关联，并设计信息融合模块获取有效的融合特征信息，基于重构误差实现高效多维时间序列异常检测.

3）在多个多维时间序列真实数据集上评估了FLAD 方法.对比实验结果表明FLAD 获得了平均最佳F1 分数0.938 3 和平均最佳精确率0.924 0，相较于最先进的方法分别提升了0.043 和0.0277.进一步地，通过消融实验、灵敏度实验分析以及时间损耗分析证明了提出的多维时间序列异常检测结构设计的合理有效性并分析了时间序列窗口大小对异常检测性能的影响.

1 相关工作

现有的无监督多维时间序列异常检测方法大致可以分为2 类：基于重构的异常检测方法和基于预测的异常检测方法.

1.1 基于重构的异常检测方法

基于重构的多维时间序列异常检测方法通过基于潜在变量重构原始输入来训练模型，学习整个时间序列的正常表示.Malhotra 等人[10]提出了一种基于长短期记忆网络（long short-term memory,LSTM）[20]的编码器-解码器框架来学习正常时间序列的表示，该模型使用输入序列作为训练数据，并对每个输入时间戳进行重构，将高重构误差的时间戳作为异常时间点.Park 等人[11]提出了一种名为LSTM-VAE 的方法，该方法将LSTM 与变分自编码器（variational autoencoders,VAE）[21]相结合，融合信号，重构期望分布.Zhang 等人[15]注意到多维时间序列数据中存在多级时间依赖性，并且时间数据中存在的严重噪声会影响基于LSTM 的异常检测模型的泛化性能，从而提出了多尺度卷积递归编码器-解码器（multi-scale convolutional recurrent encoder-decoder,MSCRED）将一个输入序列窗口转换成多尺度的归一化矩阵，然后通过卷积编码器和卷积LSTM 捕获多维时间序列的正常模式.该方法能够捕获更复杂的多模态相关性和时间信息.DAGMM[18]将自编码器和高斯混合模型进行结合，通过一个深度自编码器获取输入的低维表示和重构误差，并通过多层的递归神经网络对多维时间序列进行建模.生成对抗网络（generative adversarial network,GAN）[22]也被用于时序异常检测，其中具有代表性的方法是MAD-GAN[16]，该方法使用基于LSTM 的GAN 模型对时间序列分布进行建模，通过同时考虑整个变量集来捕捉变量之间潜在的相互作用，用于多维时间序列异常检测.Su 等人[17]认为确定性方法可能会被不可预测的数据样本所误导，提出了一种用于多维时间序列异常检测的随机模型OmniAnomaly，通过学习多维时间序列的鲁棒表示和平面归一化流来捕捉数据背后的正常模式，并将低重建概率的模式视为异常.

1.2 基于预测的异常检测方法

基于预测的多维时间序列异常检测方法训练模型时，在无异常情况下预测训练输入后的值，并将真实值与预测值之间的距离作为异常评分[23].这类方法背后存在的假设为给定的正常数据通过预测分析是可重构的，如果存在时间观测点是不可预测的，那么它很可能是一个异常值[24].将时间序列回归方法作为预测模型是一类主流的方法，经典的异常检测方法使用求和自回归移动平均模型（autoregressive integrated moving average model,ARIMA）的变种来对时间序列进行建模和检测异常行为[25].Rousseeuw 和Leroy[26]提出了一种基于自回归的异常检测方法，假设每个单独的时间点实例只与其过去的几个时间点实例线性相关，通过历史时间点数据对未来时间点数据进行建模预测，但是用线性关系对时间依赖进行建模无法捕获复杂的时间序列关系.在自回归方法的基础上，Bontemps 和Cao[27]采用具有长短时记忆单元的递归神经网络（LSTM-RNN）对时间序列之间的非线性时间相关性进行建模.LSTM-NDT[9]是一个基于LSTM 的深度神经网络模型，该模型使用输入序列作为训练数据，对每个输入时间戳预测下一个时间戳的数据，并提出一种非参数动态错误阈值（non-parametric dynamic error thresholding,NDT）策略，利用误差序列的滑动平均值设置异常阈值.Elsayed 等人[28]重新思考深度学习模型对于时间序列预测的必要性，提出了基于窗口的梯度提升回归树（gradient boosting regression tree,GBRT）方法，以窗口方式处理时间序列数据并基于分段子序列构建回归模型.然而，基于自回归的方法不能有效捕获易变的时间序列的正常模式，因此在复杂多维时间序列中的异常检测效果欠佳.Bai 等人[29]提出了将卷积运算用于时间维度的时域卷积网络（temporal convolutional network,TCN），之后Garg 等人[30]将TCN 中的卷积操作替换为转置卷积操作，提出了基于TCN 的自编码器对多维时间序列进行重构.Deldari 等人[31]鉴于TCN 处理时间序列的优越性，提出了以TCN 为特征提取网络的对比预测编码方法用于时间序列异常检测.Gugulothu 等人[32]通过端到端学习框架，将非时间维度缩减技术和循环自编码器结合起来进行时间序列建模.Deng和Hooi[33]基于图神经网络提出了图偏差网络（graph deviation network,GDN）模型用以学习数据模式之间的关系图，并通过基于注意力机制的预测和偏差评分得到异常分数.

基于重构的异常检测方法无法同时有效学习到指标度量间表示和时间依赖性，导致对于多维时序数据的重构不够充分，重构误差作为异常评分的效果不显著.基于预测的异常检测方法，由于复杂多维时间序列的不可预测性，导致其异常检测误报率偏高.本文针对上述问题设计了一种基于融合学习的多维时间序列异常检测模型，通过在时域卷积网络中引入自注意力机制，同时捕获数据局部特征和数据全局特征，并构建信息融合模块对2 种特征进行信息融合，以此捕获更加充分的时序重构信息，实现更有效的多维时间序列异常检测.

2 融合学习异常检测方法

2.1 问题定义

本文所讨论的多维时间序列是等时间间隔采样多维时间变量形成的长度为T的时间戳序列，X=（x1,x2,…,xT）.每一个时间观测点xt都是在时间戳t下获取的多维数据，xt∈Rm，∀t∈{1，2，…，T}.本文主要讨论的是m≥2 的多维时间序列异常检测问题，当m=1 时，问题就退化为单维时间序列异常检测问题.多维时间序列异常检测用于确定一个时间观测点xt是否为异常，给定一个时间序列X，需要给出对应的异常标签序列Y=（y1，y2，…，yT），yt∈{0,1}，∀t∈{1，2，…，T}.yt=0 表示时间戳t下的时间点为正常，yt=1 表示时间戳t下的时间点为异常.

2.2 数据预处理

为了提升模型的收敛速度以及精度，在多维时间序列异常检测模型训练之前需要对多维时间数据进行归一化处理:

其中min（X）和max（X）分别表示多维时间序列X中最小和最大的向量，ε是为了避免分母为0 而设置的一个很小的常向量.由于时间序列的时间关联性，即不同时间点之间存在时间依赖，考虑到时间观测点xt和历史时间点的依赖关系，构建一个长度为N的时间窗口：

对于t＜N的时间观测点xt，由于没有足够的历史时间点数据，无法构建长度为N的时间窗口.为了避免短时序窗口对模型序列正常模式重构的影响，对于t＜N的时间观测点xt，由于没有足够的信息判断其异常程度，将其视为正常时间点.因此给定一个多维时间序列X，从t=N开始进行时间窗口的构建，将其转换为一个滑动窗口序列W=（wN，wN+1，…，wT）.对于模型的训练，并不是直接将X作为模型输入，而是将多维时间序列X转化为W作为模型输入.这使得模型对于时间观测点xt的异常检测并不是只关注xt本身，而是结合xt历史时间依赖信息对时间点xt的异常情况进行评分.

具体来说，并不是直接对于输入的一个wt就给出一个对应于时间观测点xt的异常标签yt，而是首先通过模型得到一个xt对应的异常分数st，在模型训练阶段通过时间窗口的异常分数得到一个异常阈值S，当st≥S时，相对应的异常标签yt=1，否则yt=0.获取异常分数的方法是模型通过时域卷积网络以及自注意力模块，并通过模型融合信息机制分别获得多维时间序列的重构表示C1以及C2，利用C1以及C2和原始时间窗口w的差值获得异常分数.

2.3 融合学习异常检测模型

FLAD 是一个基于融合学习的无监督多维时间序列异常检测模型，整个模型是由多层的融合编码器（fusion encoder）以及单 层的融 合解码 器（fusion decoder）组成，模型整体框架如图1 所示.具体地，首先将时间滑动窗口w作为模型的2 个相同输入和，对于融合编码器而言分别存在2 个输入和2 个输出，通过融合编码器的时域卷积模块以及自注意力模块分别捕获多维时间序列在局部性上以及全局性上的数据依赖，并采用十字绣单元[34]进行提取特征的融合丰富.多层融合编码器的堆叠有利于学习到更深层次的潜在时间序列关联性.假定存在L层的融合编码器，输入长度为N的时间序列窗口w∈RN×m,对于第l层的计算过程以及模型初始输入可以方程形式化为：

其中Q，K，V∈RN×dmodel，分别代表自注意力计算中的查询、键值以及值，是由自注意力模块的输入Z2和3 个线性变换矩阵WQ，WK，WV进行线性变换得到的.WQ，WK，WV∈Rdmodel×dmodel分别是Q，K，V的参数矩阵.M∈RN×N，代表自注意力矩阵.softmax函数对自注意力矩阵的每一行进行归一化处理，使得自注意力矩阵的每一行都是一个和为1 的离散分布.TemporalBlock函数代表时域卷积操作，通过2 层的膨胀因果卷积操作获取更大的感受野，并采用残差块的结构设计防止时域卷积运算过程中产生梯度消失，具有更好的泛化能力.和I2分别是时域卷积在添加自注意力矩阵信息后和自注意力模块处理后的隐层表示.时域卷积网络相较于传统的循环神经网络（recurrent neural network,RNN）而言，可以捕获更长的时间序列依赖信息.但从本质上来看时域卷积网络依旧是卷积神经网络的变种，虽然膨胀卷积的引入可以扩大时间序列的感受野，但是相较于transformer[35]可以捕获任意长度时间序列信息的特性，时域卷积网络在全局时序信息的获取上仍然还有不足.相较于时域卷积网络更加专注于局部信息和维度间信息获取，自注意力模块可以学习到时间序列的远程依赖性，但是局部信息获取的能力较差.鉴于时域卷积网络和自注意力模块2 个模块对于多维时间序列信息的捕获各有侧重，在获取这2 个模块处理的隐层信息后，通过添加一个信息融合模块，使得学习到的2 个不同侧重的隐层表示可以进一步融合产生更加丰富的信息表示.十字绣单元是一种多任务学习的共享表示方法[35]，可以有效地将2 个模块学习到的不同信息进行共享丰富.通过在信息融合模块中引入十字绣单元，使得多层的信息融合模块可以对每一层的隐层特征进行充分地学习融合.并且由于十字绣单元通过线性变换对信息进行交互，在训练阶段反向传播时不会产生过大的时间开销.

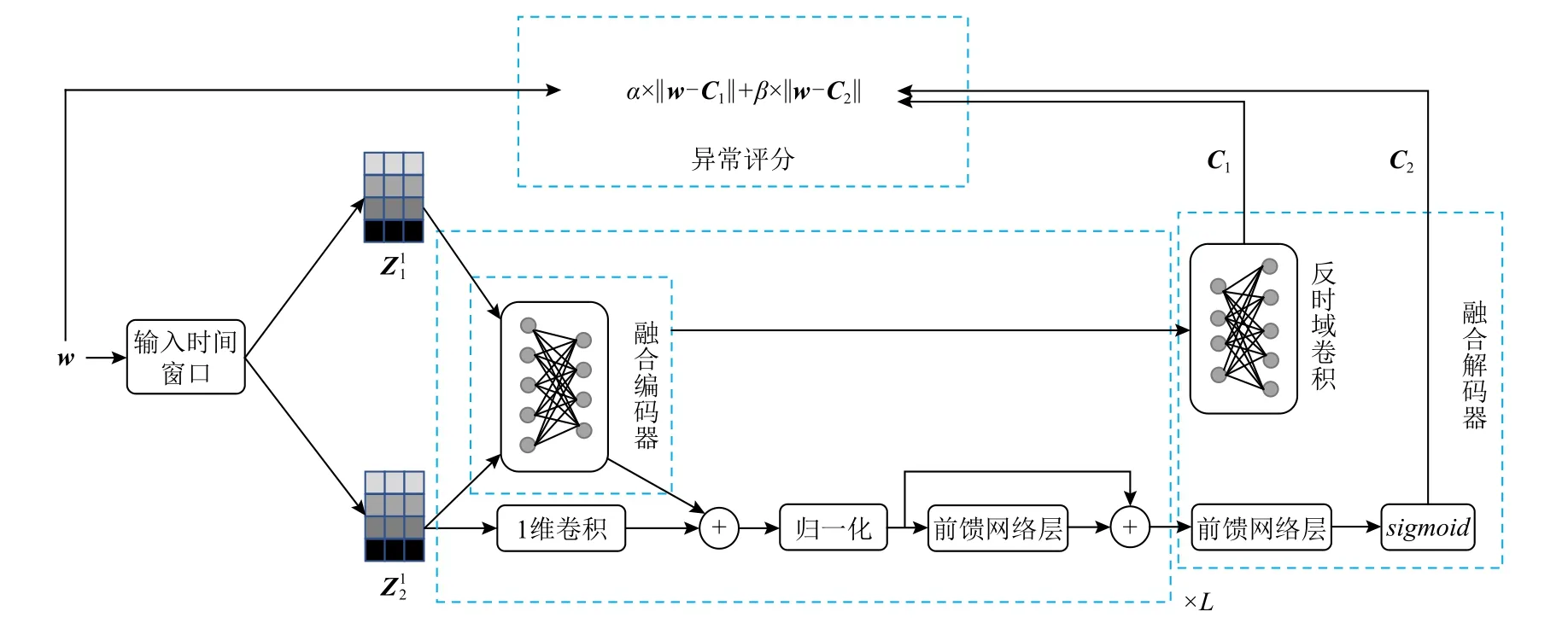
Fig.1 The overall architecture of fusion learning model图1 融合学习模型整体框架

Fig.2 Fusion encoder图2 融合编码器

融合解码器由2 个解码部分分别对第L层融合编码器最后输出的2 个隐层特征进行解码.第1 个解码部分为反时域卷积层，通过采用转置卷积替换时域卷积残差块中的膨胀因果卷积实现；第2 个解码部分由单层的前馈神经网络层以及函数sigmoid组成.

模型损失函数采用重构误差损失，以此来最小化模型原始输入时间序列和重构数据间的误差，提高模型学习到多维时间序列正常模式的能力.在模型训练阶段，融合学习模型对于多维时间序列输入w的重构表示分别是C1和C2，模型损失函数为

其中 α+β=1，α 和 β为可以设置的超参数.在模型测试阶段，通过模型获取输入w的重构表示C1和C2，同样通过式（13）计算异常评分，异常评分越高表明该时间点越异常.

3 实 验

本节在4 个现实数据集上将FLAD 方法与7 种异常检测方法进行对比，对比结果分析验证了FLAD方法异常检测性能的优越性.并进一步从消融分析、灵敏度分析以及时间损耗分析3 个角度分析论证融合学习异常检测方法的有效性.

3.1 环境和数据集

本实验是基于Pytorch 框架进行模型构建的，均在Ubuntu18.04 环境下进行.实验平台的主要硬件参数为Intel Core i9-10920X CPU，64 GB 内 存，GPU GNVIDIA TITIAN RTX，6 GB 显存.

本实验使用的数据集中包括了一个云际运维数据集ASD，FLAD 方法在该数据集上的异常检测性能大幅提升表明了该方法在云际智能运维异常检测中的优越性.除此以外，本文还选取了3 个传感器数据集，在这3 个数据集上的实验结果体现了FLAD 方法的泛化能力.下面介绍这4 个实验数据集：

1）ASD 云际运维数据集[36].该数据集收集自某大型互联网公司，一共包含了12 个实体，每个实体都描述了一个服务器的状态；包括了45 天的多维时间序列数据以及19 个指标用以描述服务器的状态（包括CPU 相关指标、内存相关指标、网络指标等）.数据集的观测结果为等间隔5min.前30 天数据作为训练集，后15 天数据用于测试集.测试集中的异常已经由系统操作员根据事件报告和领域知识进行标记，数据集中的异常大致可分为时间异常、度间异常和度间时间异常3 种类型.

2）MSL 数据集[9].该数据集是由NASA 的火星探测漫游者本身的传感器和执行器数据组合而成，包含27 个多维时间序列数据，每个多维时间序列数据由55 个维度的传感器信息组成，数据集中的异常可分为点异常和上下文异常.

3）SMAP 数据集[9].该数据集和MSL 数据集相似，是由NASA 的火星探测漫游者使用的土壤样本和遥感信息组成的数据集.数据集包含55 个多维时间序列数据，每个多维时间序列数据由25 个维度的传感器信息组成，数据集中的异常可分为点异常和上下文异常.

4）MIT-BIH 心电图数据集[37].该数据集包含了位于波士顿的贝斯以色列医院的48 个患者的心电图记录.该数据集通过随机异常分数[38]进行了筛选，留下了命名为113，123，202，203，209，210，220 的记录.

实验所用到的这4 个数据集统计如表1 所示.

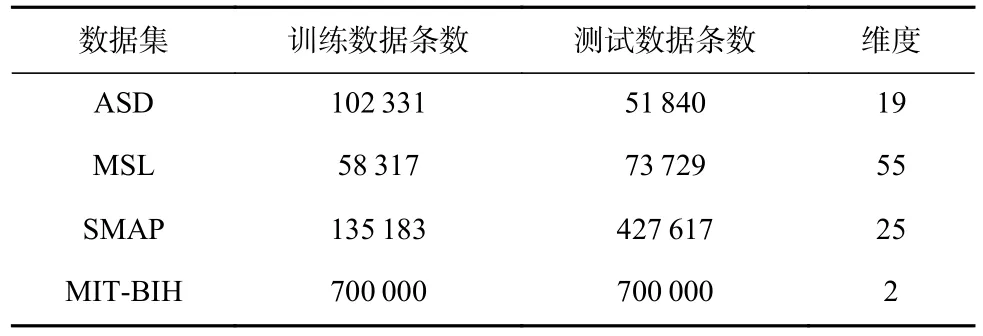
Table 1 Dataset Statistics表1 数据集统计信息

3.2 评价指标

本文使用精确率（precision，P）、召回率（recall，R）、F1 分数、平均精确率（average precision，AP）以及AUC（area under curve）共5 个指标来评估模型性能.

TP表示正确检测为异常的异常，FP表示错误检测为异常的正常，TN表示正确识别为正常的正常，FN表示错误识别为正常的异常.AP和AUC分别通过计算PR（precision-recall）曲线下的面积和ROC（receiver operating characteristic）曲线下的面积得到.

计算AP的PR 曲线如图3 所示，表示的是精确率P和召回率R的关系，横坐标为召回率R，反映了异常检测器对实际异常的覆盖能力，纵坐标为精确率P，反映了异常检测器检测异常的准确程度.依次改变置信度为0～100%，得到多组召回率和精确率组成的坐标，将坐标相连得到PR 曲线.

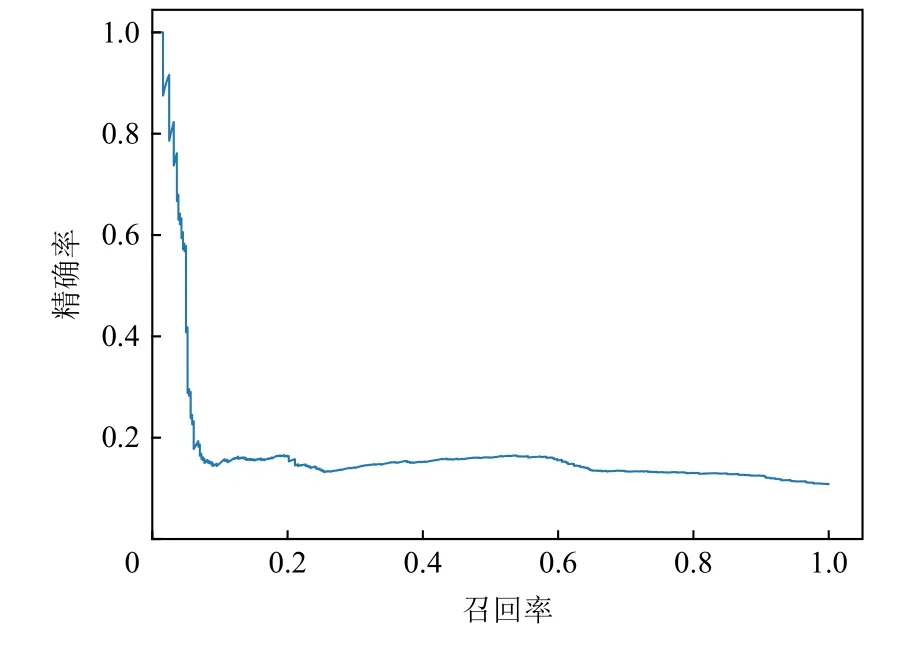
Fig.3 PR curve graph图3 PR 曲线图

计算AUC的ROC 曲线如图4 所示，表示的是假阳性率（false positive rate，FPR）和真阳性率（召回率）的关系，横坐标为假阳性率，纵坐标为真阳性率（召回率）.依次改变置信度为0～100%，得到多组假阳性率和真阳性率组成的坐标，将坐标相连得到ROC 曲线.FPR表示检测为异常但实际为正常的实例在所有正常实例中的比例，计算公式为：

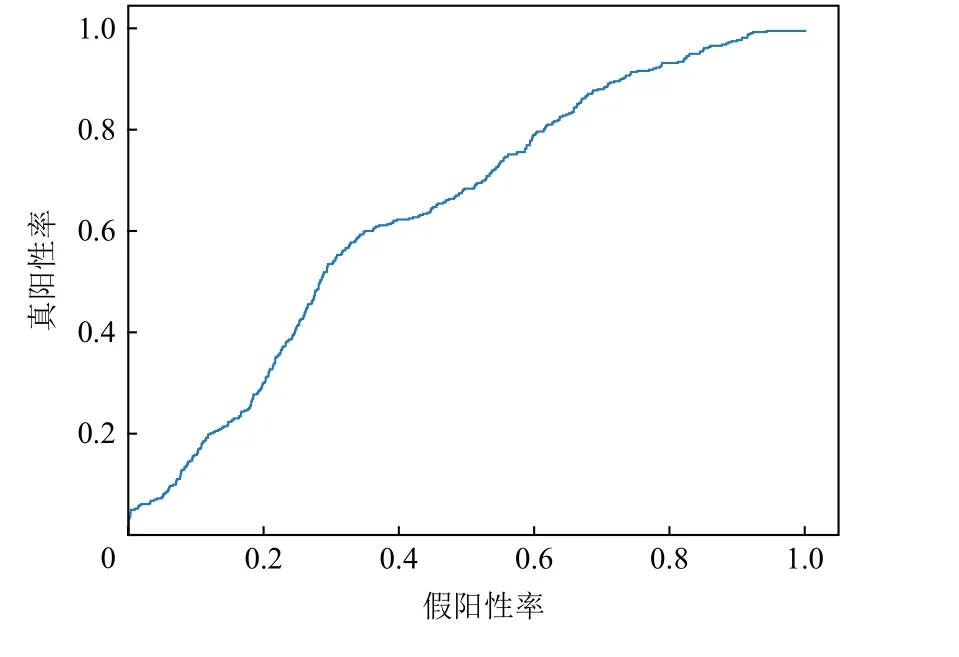
Fig.4 ROC curve graph图4 ROC 曲线图

本实验为每一个观测时间点计算一个异常分数，异常分数越大说明该观测时间点越异常.在实际的应用场景中，异常点一般都是连续出现，形成一个连续的异常段.因此只要求模型在异常段内检测出异常点，而并不要求模型将异常段内的所有点都检测为异常是合理的.所以实验采用了一种点调整策略[39]来提高异常检测器的性能，该策略已经在很多工作上[3,8,18,36]被证明是有效的.具体来说，如果一个真实异常时间段内的任意一个观测时间点被检测为异常，就认定该异常时间段检测正确，而对于真实异常时间段以外的检测仍按照常规处理.本文实验采用点调整策略进行指标的计算.

3.3 对比方法

本文将所提FLAD 方法与2 种经典的多维时间序列异常检测方法以及5 种目前最先进的深度多维时间序列异常检测方法进行对比，验证FLAD 方法的有效性.

1）iForest[40].孤立森 林（isolation forest，iForest）是一个基于集合的高效异常检测方法，该方法将分布稀疏且远离高密度群体的点作为异常点.iForest 随机选取一个超平面切割数据空间，每一次切割都会生成2 个子空间，将这个操作一直循环下去直到每一个子空间都只有一个数据点.相较于稀疏分布远离密集点的数据集合，那些高密度群体需要经过更多次的子空间切割才会停止.通过不断反复地从头随机切割，平均切割结果对于切割次数小于阈值的数据集合检测为异常.iForest 具有线性时间复杂度，适合大规模数据的异常检测，但是由于每次切割都是随机选择1 个维度，导致随机森林构建完依旧存在大量的维度信息没有利用的情况，这使得该方法不适用于高维度的时间序列异常检测.

2）COPOD[41].COPOD 是一种基于copula 的异常检测方法，copula 是一种概率统计函数，可以构建多维度间的相关性，对多个指标间的依赖关系进行建模.COPOD 从偏离均值的尾端概率判断异常的思想出发，通过经验累积分布估计所有维度联合分布的尾端概率.该异常检测方法检测速度快，对于维度异常具有一定的可解释性，然而经验累积分布构建过于简单，对于时间依赖的建模效果欠佳.

3）DAGMM[18].DAGMM 是一个基于自编码器和高斯混合模型的深度无监督学习模型，通过一个深度自编码器获取输入的低维表示和重构误差，并通过多层的递归神经网络对多维时间序列进行建模.之后通过重构误差和高斯混合函数似然函数对模型进行优化，2 种网络的解耦训练让整个模型更加具有鲁棒性.然而，这样的循环优化导致模型训练速度慢，并且对于度量间的依赖关系捕获有所欠缺.

4）TCN AE[30].TCN AE 是一个基于TCN 的自编码器.TCN 通过引入膨胀因果卷积，能够跨时间步对时间序列进行特征提取，相较于LSTM 传统的时间序列建模更有优势.通过将原始TCN 作为编码器，然后对TCN的残差块进行堆叠，并将TCN 残差块中的膨胀因果卷积替换为转置膨胀因果卷积，构建解码器，基于重构误差检测异常.该模型擅长提取数据局部特征以及度量间的特征，由于卷积操作导致感受野受限，对于全局数据关联性的捕获不足.

5）LSTM AE[10].LSTM AE 是一个基于LSTM 的自编码器.LSTM 是一种特殊的RNN，相较于RNN，LSTM 能够处理更长的序列数据.由于LSTM 的设计适合处理时序数据，LSTM AE 能够学习到丰富的时间依赖，基于重构误差对多维时间序列进行异常评分.但是同样由于LSTM 结构设计的缺陷，在同一时间只能对单个时间数据进行处理，导致模型训练速度慢，计算成本高.

6）OmniAnomaly[17].OmniAnomaly 是一种随机递归神经网络，利用随机变量连接、平面归一化流等关键技术，通过学习多元时间序列的鲁棒表示来获取其正常模式，通过特征表示来重构输入数据，并利用重构概率来确定异常.该方法创新地将门控循环单元（gated recurrent unit，GRU）和VAE[21]进行结合，模型同时考虑了多维时间序列的时间依赖性和随机性.

7）GDN[33].GDN 是一种基于图神经网络的多维时间序列异常检测方法，它学习数据模式之间的关系图，并通过基于注意力机制的预测和偏差评分得到异常分数.通过图神经网络对维度间依赖关系图进行构建，能够有效学习到维度间依赖，并且对于维度间的偏差异常有较好的可解释性，是一个优异的多维时间序列异常检测深度模型.

3.4 实验设置

在本实验中，FLAD 方法包含了3 层编码层和单层的解码层，每一个隐层通道数都是64，滑动时间窗口大小设置为100，关于时间窗口大小对于模型异常检测性能的影响将在3.7 节进行详细的分析.在模型训练阶段，设置样本批量训练大小为128，采用早停策略在100 个迭代轮次内训练，采用初始学习率为0.000 15 的ADAM 优化器对模型进行优化.将优化函数 式（12）中的共 享参数 α11，α12，α21，α22分别设置为0.8，0.2，0.2，0.8.将式（13）中目标函数的分配权重 α和β分别设为0.5 和0.5.实验中，应用了数据集的原始划分得到训练集和测试集，挑选训练集中的25%作为实验验证集，将训练集剩余部分作为实验训练集.为了进一步确保实验的可信性以及稳定性，本实验对每个数据集都进行5 次重复实验，最终实验结果取5 次重复实验结果的平均值.

3.5 对比结果分析

7 种多维时间序列异常检测方法在4 个多维时间序列数据集上的对比实验结果如表2 所示.对FLAD 在4 个数据集上的4 个F1 分数以及AP取平均，其平均F1 分数为0.9383，平均AP为0.9254，优于征更加丰富的FLAD 方法能够检测出绝大部分ASD数据集上的异常，在各个性能指标上都超出对比算法很多，证明在复杂云际运维异常数据集上，FLAD方法具备捕获到更加丰富特征的能力.相较于ASD数据集的复杂异常，MSL 和SMAP 数据集的异常分布以及异常形式较为简单，大部分异常检测方法都能够取得较好的F1 分数.FLAD 在MSL 和SMAP 两个数据集上的F1 分数相较于对比算法中的最优F1分数分别提高了0.0208 和0.0119，证明在短时间序列数据上FLAD 依旧可以有效融合局部数据信息和全局数据信息，对于细微的异常检测更加敏感.在MITBIH 数据集上，对于这种有明显周期性的FLAD 和GDN 都表现出了优越的异常检测性能，FLAD 在F1分数上略高于GDN 的F1 分数.综上，本文提出的FLAD能够更加有效学习多维时间序列的时间依赖和维度间依赖，在数据局部性上和数据全局性能够构建更加丰富的特征表示，弥补了之前的多维时间序列异常检测方法无法同时捕获多层次信息依赖的缺陷.所有对比算法.在MSL 数据集上，COPOD 方法有最高的召回率（1.000 0）；在SMAP 数据集上，GDN 方法有最高的召回率（1.000 0）；在MIT-BIH 数据集上，GDN 方法有最高的精确率（0.873 5）以及最高的AP值（0.8499）.除此以外，FLAD 在4 个数据集上的其余性能指标都优于目前最流行的多维时间序列异常检测方法，证明FLAD 的融合学习方法帮助模型学习到了更好的时间依赖和度量间依赖以及数据局部和数据全局特征.具体来说，FLAD 在ASD 数据集上的F1 分数相较于对比算法中的最优F1 分数提高了0.0882.iForest，COPOD，DAGMM，TCN AE，LSTM AE主要对时间依赖进行建模，对局部数据时间依赖更加敏感.OmniAnomaly 更加关注度量间异常，GDN 通过图神经网络对度量间的依赖有很好的构建，但是OmniAnomaly 和GDN 两种方法对于时间上的依赖关系关注度都不够.而ASD 数据集是一个复杂云际运维数据集，异常类型包括时间异常、度量间异常以及度间时间异常.因此通过信息融合机制构建信息特

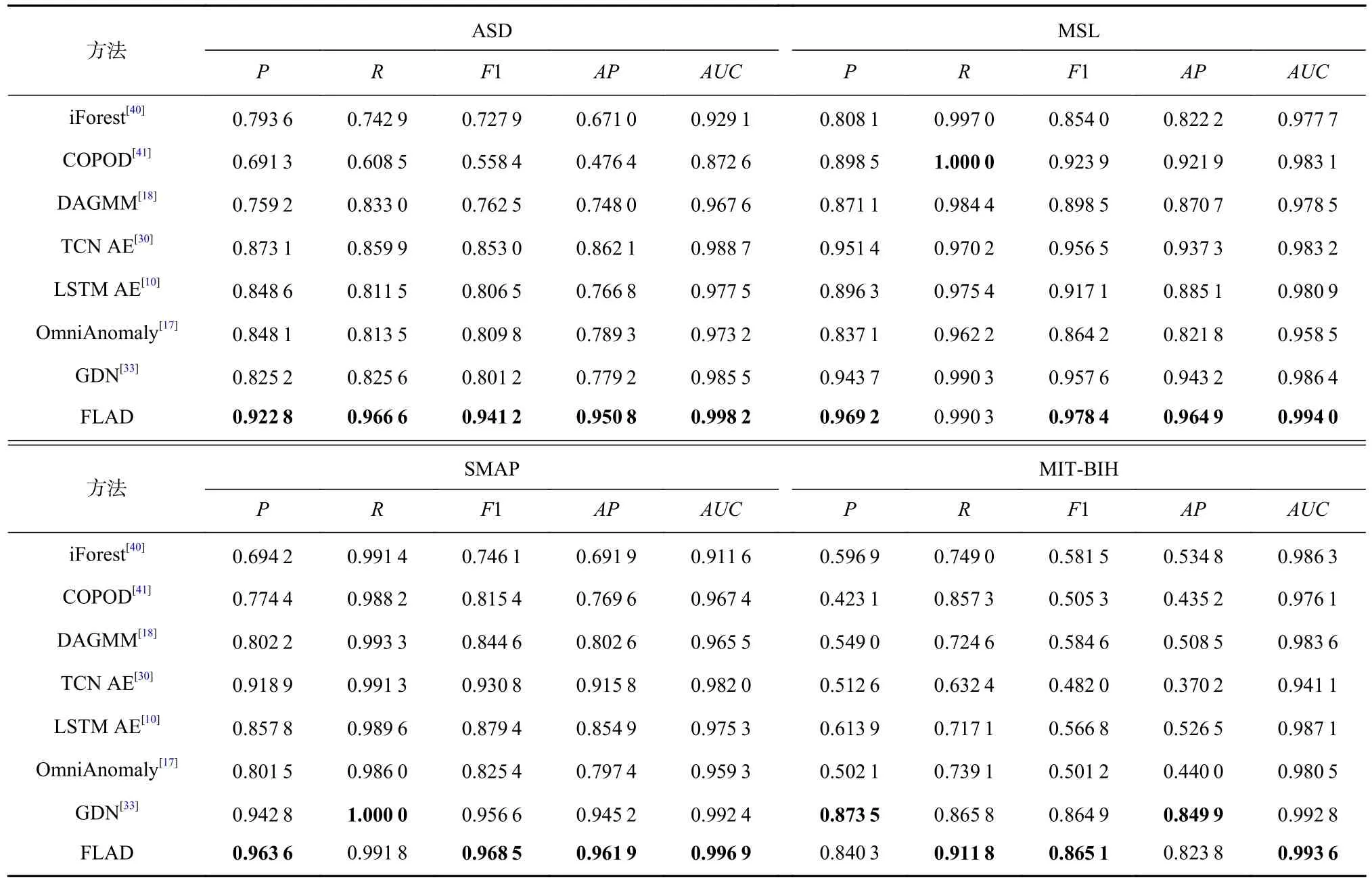
Table 2 Anomaly Detection Comparison Results表2 异常检测对比结果

3.6 消融分析

为了进一步验证本文设计的各个模块机制的合理性和有效性，本节在全部实验数据集上进行FLAD模型的消融实验.4 种模型结构分别为：据局部上更加丰富有效的特征.引入了自注意力机制的FLAD w/o CU 模型相较于普通并行学习的FLAD w/o ALL 模型，在全部实验数据集的平均F1 分数上提高了0.0077，证明自注意力机制的引入有助于模型更加关注全局信息，但是缺乏信息融合模块导致模型无法充分学习全局信息，导致模型的提升效果一般.本文原始的FLAD 模型相较于只保留了信息融合模块的FLAD w/o SA 模型在所有实验数据集的平均F1 分数以及平均AP上分别提升了0.0156 和0.0098；相较于只保留了自注意力机制的FLAD w/o CU 模型在所有实验数据集的平均F1 分数以及平均AP上分别提升了0.1105 和0.1107；相较于FLAD w/o ALL 模型在所有实验数据集的平均F1 分数以及平均AP上分别提升了0.1182 和0.1267.消融实验结果分析证明，融合学习模块和自注意力机制的结合使得模型能够同时捕获多维时间序列在局部性和全局性上的信息依赖，从而表现出更好的异常检测性能.

1）FLAD 模型.本文提出的原始模型，使用采用自注意力机制并添加信息融合模块的编码部分.

2）FLAD w/o（without）SA 模型.在FLAD 原始模型中的编码部分去除了自注意力机制，依旧保留了信息融合模块.

3）FLAD w/o（without）CU 模 型.在FLAD 原始模型中的编码部分去除了信息融合模块，依旧保留了自注意力机制.

4）FLAD w/o（without）ALL 模型.在FLAD 原始模型中的编码部分同时去除了信息融合模块以及自注意力机制，此时FLAD 模型退化为2 个并行运算的子模型，特征之间没有任何的信息融合.

以上4 种模型在全部实验数据集上的P、R、F1 分数、AP以及AUC这5 个性能指标上的实验结果如表3 所示.加入了信息融合模块的FLAD w/o SA 模型相较于普通并行学习的FLAD w/o ALL 模型，在所有实验数据集的平均F1 分数上提高了0.1026，证明信息融合模块的引入有助于模型学习到数据全局和数

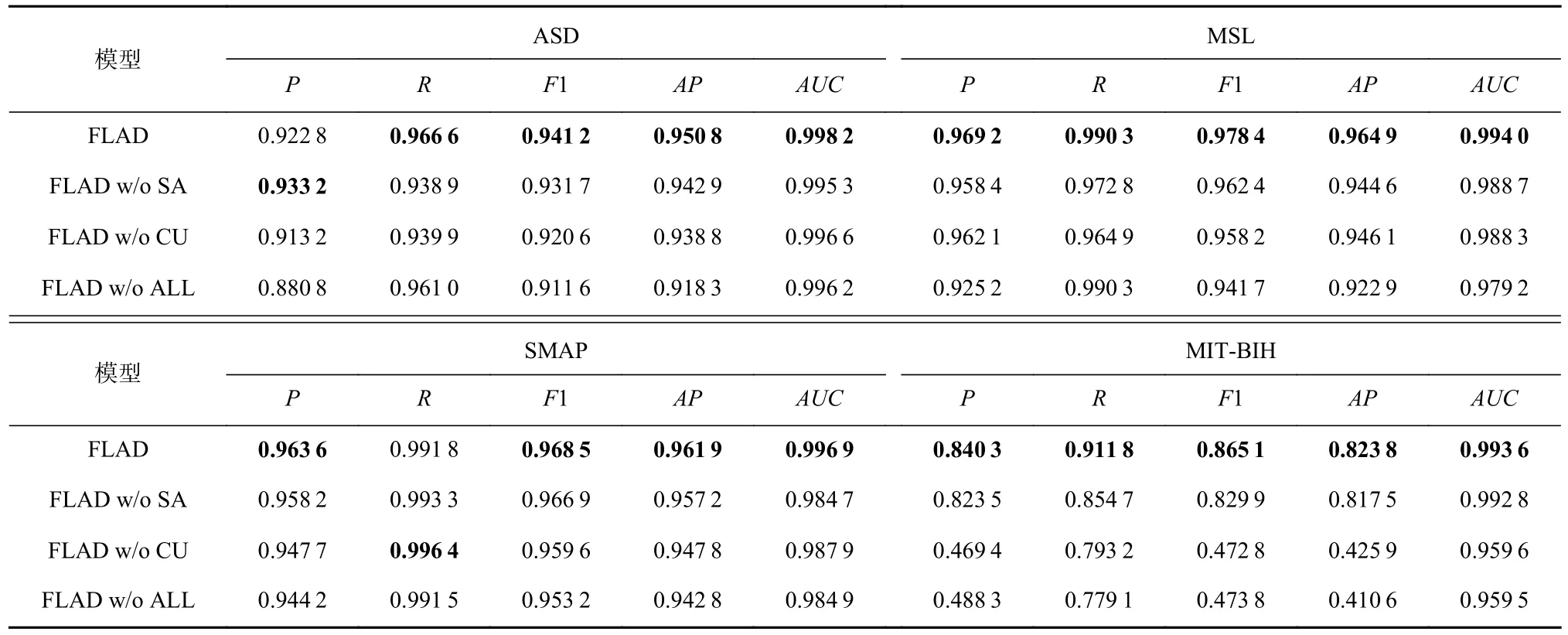
Table 3 Ablation Study表3 消融实验

3.7 灵敏度分析

考虑到时间序列窗口大小对FLAD 模型以及3个消融模型的异常检测性能可能产生的影响，本文还在F1 分数、AP以及AUC三个性能指标上进行了灵敏度分析，实验结果如图5 所示.各个模型的异常检测性能一开始随着窗口的增大而提升，这是因为当时间序列窗口过小时，输入时间序列无法很好表征局部的上下文信息.但是当时间序列窗口过大时，细微的局部异常更加容易隐藏在大量的正常时间点之中，反而使得异常检测效果下降.当时间序列窗口大小为100 时FLAD 模型在各个性能指标上都表现最优异，因此在本实验中采用大小为100 的时间序列窗口.

3.8 时间损耗分析

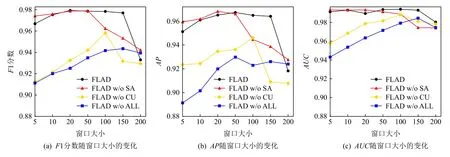
Fig.5 Variation of F1,AP and AUC with window size图5 F1，AP 以及AUC 随窗口大小的变化

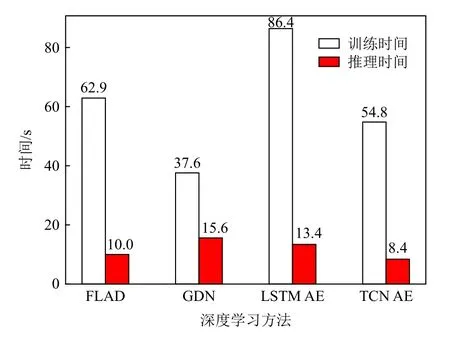
Fig.6 Graph of time loss图6 时间损耗图

为了进一步探究FLAD 在智能运维场景中的可用性，本文对FLAD 和对比方法中的主流深度学习方法在ASD 数据集下单轮训练测试的训练时间和推理时间进行了评估，实验结果如图6 所示.从单轮训练时间损耗来看，本文提出的FLAD 高于GDN 以及TCN AE，低于LSTM AE.从智能运维实际应用的场景出发，例如在线实时异常检测，推理时间的损耗更加影响异常检测方法实际的应用.在单轮推理时间损耗上，FLAD 低 于GDN 以 及LSTM AE，略高于TCN AE.时间损耗实验表明相较于之前的主流深度学习方法，FLAD 在异常检测性能上有大幅提升的同时，并没有因为网络结构的复杂化而导致时间损耗过大.而这也得益于信息融合模块采用线性变换的方式对数据进行交互，在训练推理过程中并没有引入复杂的数据运算.由此可见，本文提出的FLAD 方法具有很强的可用性.

4 总结与展望

多维时间序列的异常检测是云际智能运维的重要任务.本文提出了一种基于融合学习的无监督多维时间序列异常检测方法FLAD，该方法使用模型设计的时域卷积模块和自注意力模块对多维时间序列的数据局部依赖性和数据全局依赖性同时进行建模，并通过十字绣单元的信息共享机制对特征信息进行融合.FLAD 在4 个多维时间序列数据集上的异常检测性能优于目前最先进的异常检测方法，证明了本文多层融合自编码器结构、自注意力机制以及信息融合模块的设计在学习丰富的正常数据信息从而利用重构误差进行多维时间序列异常检测的有效性.

在未来的工作中，我们打算进一步调整信息融合模块的网络结构，考虑多维时间序列在更多特征空间中的关联性，通过将更多层次的特征信息进行融合以达到更好的多维时间序列异常检测效果.

作者贡献声明：周小晖提出主要研究思路，完成实验并撰写论文；王意洁提出实验方案和指导意见，修改和审核论文；徐鸿祚协助完成部分实验，提出论文修改思路；刘铭宇指导论文写作，参与论文修订.