融合线性插值和对抗性学习的深度子空间聚类

江雨燕，陶承凤，李 平

(1.安徽工业大学 管理科学与工程学院，安徽 马鞍山 243032；2.南京邮电大学 计算机学院，江苏 南京 210023)

0 引 言

目前，聚类问题已涉及到许多实际应用程序，成为计算机视觉的重要组成部分。例如，图像分割[1]、运动分割[2]和人脸聚类[3]等。聚类作为无监督学习领域的一项关键技术，其通过发现数据间的内在结构，将相似的数据点划分到同一个簇中[4]。传统的聚类方法可以分为划分式聚类算法、基于密度的聚类算法、基于图的聚类算法、基于层次的聚类算法、基于高斯混合模型的聚类算法。典型的K-means聚类[5-6]通过确定簇心，并计算各个数据点到簇心的距离，来划分数据样本类别；谱聚类[7]把所有数据看作空间中的点，样本点之间用带权重的边相连、建立图论关联，通过切图来达到聚类的目的。尽管以上传统方法各有擅长的聚类情形，但是当面对高维复杂数据时，不能有效地进行处理。

针对高维复杂数据，文献[8]提出了子空间聚类算法，该算法是基于无监督的方式将样本集合分成不同的簇，使同簇内的样本尽可能相似，不同簇的样本尽可能相异。具有代表性的算法有：稀疏子空间聚类(Sparse Subspaces Clustering，SSC)[9-10]和低秩子空间聚类(Low-Rank Subspaces Clustering，LRSC)[11]等。然而子空间聚类算法仅对线性数据结构具有良好的处理效果，而不能有效地处理非线性问题。

近年来，随着深度学习的进展，提出了一种基于深度神经网络来解决非线性问题的方法(深度聚类方法)，该方法可以看作是通过自编码器预训练获取低维的隐表示+无监督学习微调的一个过程。现有的深度聚类算法包括：深度k-means聚类[12]、深度密度聚类[13]、深度子空间聚类[14-15]等。其中，深度子空间聚类网络(Deep Subspace Clustering Net，DSC)将自编码器与子空间聚类相结合具有深远的影响，该算法以无监督的方式，通过编码器非线性地将输入数据映射到一个特征空间，在此空间中，把每个数据样本利用自表达特性表示为同一子空间中其他样本的线性组合，以形成近邻矩阵。

尽管现有深度聚类算法在一定程度上解决了复杂结构数据聚类问题，但是，此类方法有以下局限性：(1)通常无法有效处理难分类样本，对临界簇间的数据样本不能明确分类；(2)模型没有改变隐表示的学习位置，仅使数据点与其指定的簇中心的距离最小化，使现有簇之间的距离最大化，不能有效分离个体聚簇。针对深度聚类算法的缺点，该文在深度子空间聚类模型的基础上进行改进，提出了融合线性插值和对抗性学习的深度子空间聚类(Deep Subspace Clustering by Fusing Linear Interpolation and Adversarial learning，DSC-IA)。

本模型为学习更好的低维隐表示以处理难分类样本且有效分离个体聚簇，引入了插值训练方法和对抗性学习，该方法在编码器部分使用混合函数和来自均匀分布的α系数以形成混合输出。新混合输出数据通过解码器重构数据集，为了确保重构输出与易分类样本更加类似，在混合重构集上训练一个鉴别器Dw(x)，用于预测混合函数的α系数。通过对DSC方法的改进，本模型中对抗自编码器的目标是通过预测α系数始终为0来欺骗鉴别器，同时，“混合重构”损失项也应增加到自编码器的损失函数中。总之，该文主要研究在无监督场景下的深度子空间聚类模型中如何加入插值训练方法和对抗性学习来提升聚类精度。

1 相关工作

1.1 子空间聚类

子空间聚类算法是基于无监督的方式将样本集合分成不同的簇，使同簇内的样本尽可能相似，不同簇的样本尽可能相异。求解子空间聚类问题的方法包括两个步骤：首先，构造近邻矩阵，通过测量每一对数据点的亲和性来完成；然后，对近邻矩阵进行归一化切割[16]或谱聚类[7]。但是此算法主要是依赖于线性方法，无法处理复杂结构的高维数据，因此，近年提出的深度子空间聚类模型逐渐受到关注和研究，并被广泛应用于人脸识别、自然图像的聚类与分割等场景。

1.2 深度子空间聚类

深度子空间聚类模型如图1所示，使用阴影圆表示数据向量、阴影方块表示卷积或反卷积后的通道，不强制设置相应的编码器层和解码器层的权重相同。

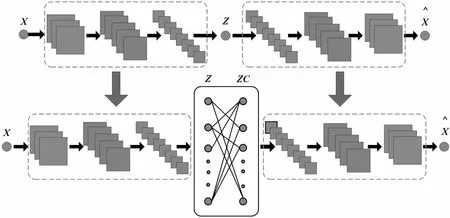
图1 深度子空间聚类

该模型主要利用自编码器自表达层的特性，具体地，给定从多个线性子空间{Si}i=1,2,…,k中提取的数据点{Zi}i=1,2,…,N(Zi∈Rd×m)，可以将子空间中的一个点表示为同一子空间中其他点的线性组合，这个属性被称为自表达性[14]。如果将所有的点zi堆叠到数据矩阵Z的列中，自表达属性可以简单地表示为一个等式，即Z=ZC，其中C(C∈Rm×m)是自表达系数矩阵。在子空间是独立的假设下，通过最小化C的某些范数，C保证具有块对角结构，即cij=0(如果点zi和点zj位于同一个子空间中)。因此，可以利用矩阵C来构造谱聚类的近邻矩阵。在数学上，这个想法被形式化为优化问题：

min‖C‖ps.t.Z=ZC,(diag(C)=0)

(1)

其中，‖·‖p表示一个任意的矩阵范数，而C上的可选对角约束防止了稀疏性诱导范数的平凡解，如L1范数。现在已经提出了C的各种规范，例如，稀疏子空间聚类(SSC)[9]提出的L1范数；低秩表示(LRR)[17]和低秩子空间聚类(LRSC)[11]中的核范数，以及最小二乘回归(LSR)[18]和有效密集子空间群(EDSC)[19]中的弗罗比尼乌斯范数。为了更好地解释数据损坏的原因，(1)中的等式约束通常作为一个正则化项，即：

s.t. (diag(C)=0)

(2)

2 DSC-IA模型

深度子空间聚类模型与其他传统的聚类模型相比较，聚类精度已经有了很大的提高，但是在对于难分类样本、能否有效分离个体聚簇问题上还存在一定的不足。针对上述两个问题，该文提出了DSC-IA模型(如图2所示)，该图展示了一个具有三层卷积编码器层、一个自表达层和三层反卷积解码器层的对抗自编码器。首先，将样本数据编码为低维隐表示；然后，对其进行线性插值，用▲和表示两个难分类样本，使用混合函数和混合系数进行混合表示，新数据进入自表达层；最后，通过解码器得到重构数据。特别地，在解码器部分训练鉴别器用于预测混合系数，使得Zα的隐表示更加适合子空间聚类。在训练期间，通过预训练对整个网络进行初始化微调。

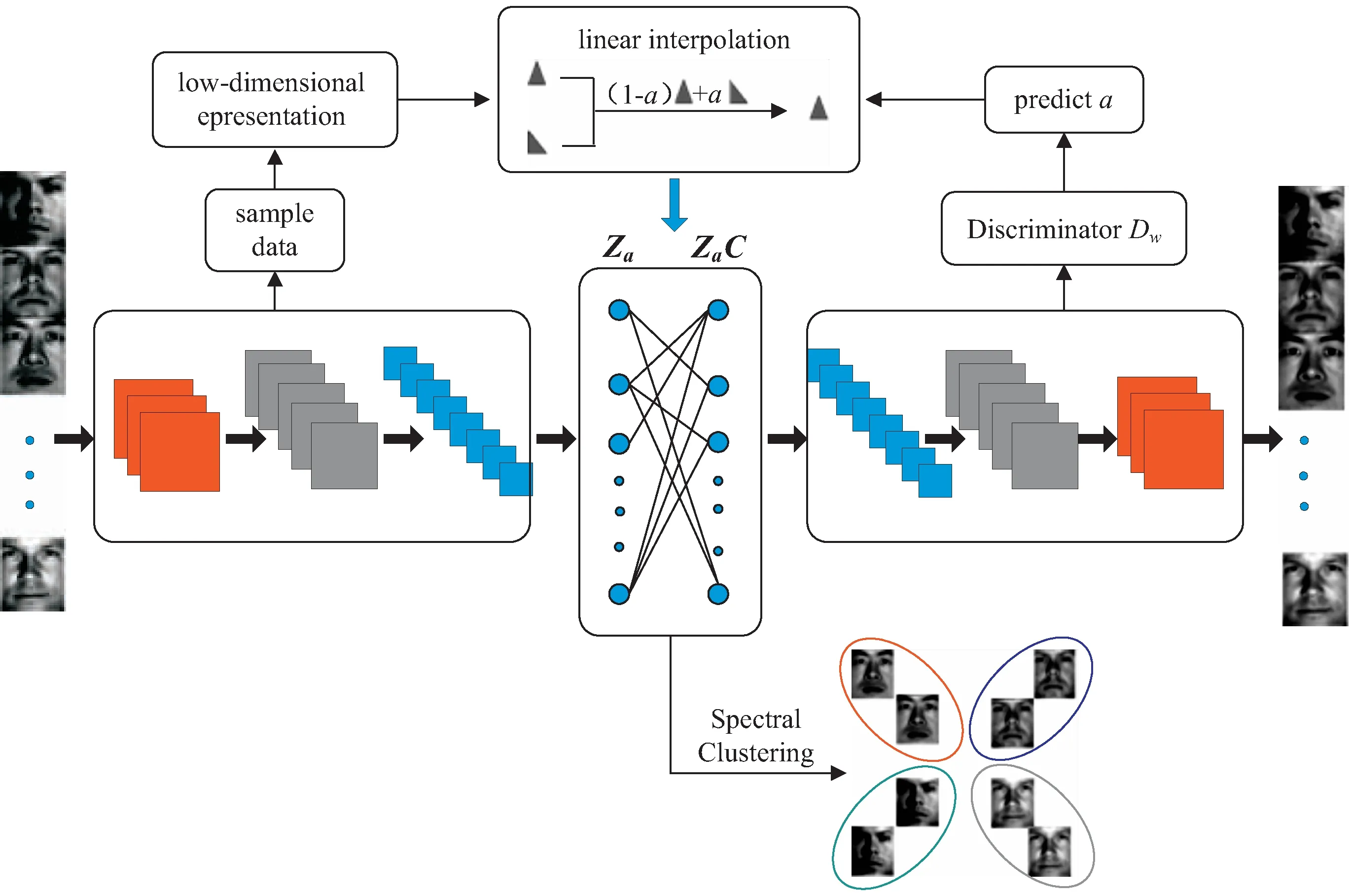
图2 融合线性插值和对抗性学习的深度子空间聚类

2.1 DSC-IA的目标函数

首先，设定一个对抗自编码器模型F(·)，其由编码器部分fe(x)和解码器部分gd(fe(x))组成。对于给定一对输入{x(i),x(j)}∈X(X∈Rd×m)，将它们编码为低维隐表示z(i)=fe(x(i))和z(j)=fe(x(j))，其中{z(i),z(j)}∈Z(Z∈Rl×m)。然后，使用混合函数和混合系数α将它们混合，得到k个混合数据：

(3)

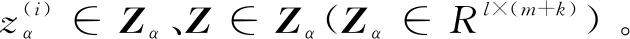
(4)

L2=‖x-gd(fe(x))‖2

(5)

其中，e和d表示对抗自编码器的学习参数。

(6)

(7)

其中，γ是一个标量超参数，第一项用来预测α系数，第二项用来提高训练稳定性。

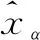
(8)

因此，在DSC-IA中，对抗自编码器的部分目标是产生实际的混合重构，使它看起来像来自用于混合操作的数据点之一。为了在无监督的子空间聚类背景下说明DSC-IA，该文对从数据集中输入的m个数据点{x(1),x(2),…,x(m)}∈X(X∈Rd×m)的样本批次处理，并尽量减少以下损失：

s.t. (diag(C)=0)

(9)

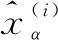
参数符号说明如表1所示。

表1 参数符号说明

2.2 DSC-IA的算法流程

由于从零开始直接训练一个具有数百万个参数的网络很困难，该文仍然采用深度子空间聚类使用的预训练+微调策略。这在避免平凡的全零解的同时，最小化式(9)中的损失函数。

如图1所示，首先，对所有数据进行了深度自编码器的预训练，而没有自表达层。然后，使用训练好的参数来初始化网络的编码器层和解码器层。最后，进行谱聚类得到聚类结果。

具体优化流程如算法1所示：

算法1：DSC-IA

输入：原始数据X，参数λ1,λ2,λ3。

输出：聚类结果。

预训练：

1.经过编码器层计算潜在表示z(i)=fe(x(i))；

微调阶段：

1.根据鉴别器在式(7)中的损失函数，通过梯度下降法来更新该鉴别器；

2.根据其在式(9)中定义的损失函数，通过梯度下降法来更新自编码器。

初始化：使用训练后的参数来初始化网络的编码器层和解码器层。

通过自表达层Zα-ZαC构建近邻矩阵C；

将C应用谱聚类方法求出聚类结果。

3 实验及结果分析

3.1 数据集

为了验证所提算法的有效性，使用几种较为常见的聚类算法在三种数据集(包括：Extended Yale B[20]、ORL[21]、COIL20[22])进行实验测试。在同一数据集进行10次独立实验，取平均值作为最终实验结果。实验环境为Microsoft Windows 10，处理器为英特尔酷睿i7，内存容量8 GB，显卡配置为MVIDIA GeForce 920M。

3.1.1 Extended Yale B数据集

Extended Yale B数据集是一个流行的子空间聚类基准。它由38名受试者组成，每名受试者在不同姿势和光照条件下均获得64张面部图像，并将图像的大小调整为42×42，该数据集的样本图像见图3(a)，网络参数设置见表2。

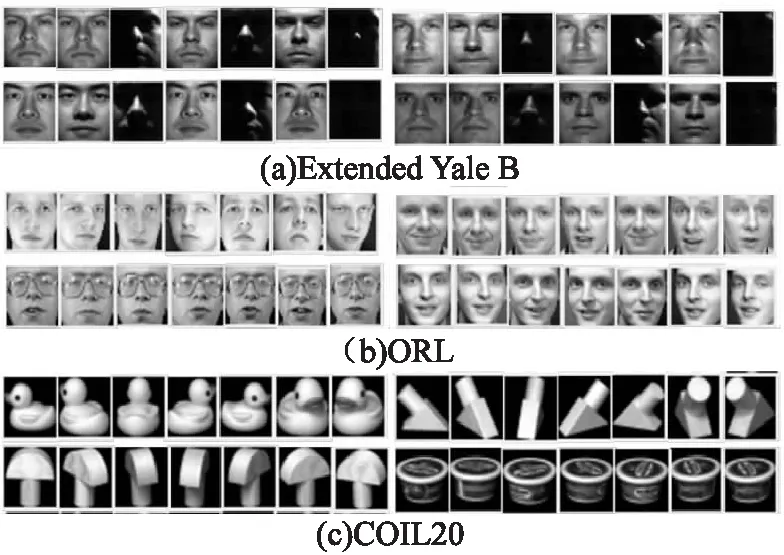
图3 样本图像

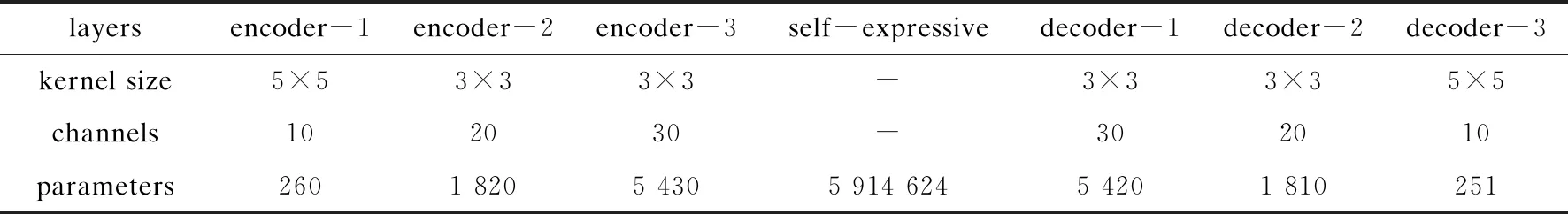
表2 Extended Yale B数据集的网络参数设置

3.1.2 ORL数据集

ORL数据集有40名受试者，每名受试者有10个样本，共由400张人脸图像组成。对于每名受试者，这些图像是在不同的光照条件下拍摄的，并且带有不同的面部表情(睁眼/闭眼、微笑/不微笑)、面部饰品(有/无眼镜)，将这些图像的大小调整为32×32，该数据集的样本图像见图3(b)，网络参数设置见表3。

表3 ORL数据集的网络参数设置

3.1.3 COIL20数据集

COIL数据集是由灰度图像样本组成，COIL20包含20多个受试对象，共由1 440张图像组成，受试对象的类型多种多样，如鸭和车型等；此数据集在黑色背景的转盘上，每个物体每隔5度拍摄72张图像，即同一对象以不同的角度捕获不同样本。在实验中，图像的大小被调整为32×32，该数据集的样本图像见图3(c)，网络参数设置见表4。

表4 COIL20数据集的网络参数设置

3.2 评价指标

该文使用了两种流行的聚类指标(即精度(ACC)和归一化互信息(NMI))来评估所有方法的聚类性能，ACC和NMI的值越大，聚类性能就越好。

ACC被定义为：

(10)

其中，yi是标签，ci是模型的聚类分配，m(·)是聚类分配和标签之间的映射函数，1(·)是指示器函数返回1或0。

NMI定义为：

(11)

NMI计算互信息得分I(Y,C)，然后根据熵函数H的数量对其进行归一化，以解释聚类的总数[23]。

3.3 结果分析

将该方法与以下几种方法在上述数据集上进行了比较，包括：稀疏子空间聚类(Sparse Subspace Clustering，SSC)[9]、核稀疏子空间聚类(Kernel Sparse Subspace Clustering，KSSC)[24]、低秩表示法(Low Rank Representation，LRR)[17]、SSC与预训练的卷积自编码器功能相结合的方法(AE+SSC)[25]、深度子空间聚类(Deep Subspace Clustering，DSC)[14-15]。

稀疏子空间聚类(SSC)：通过将每个数据点表示为来自同一子空间的其他数据点的稀疏线性组合构造子空间的数据近邻矩阵。

核稀疏子空间聚类(KSSC)：通过核技巧将SSC扩展到非线性流形。

低秩表示法(LRR)：在所有可以表示数据样本基的线性组合的候选对象中寻求最低的线性表示。

AE+SSC：结合SSC和自编码器的优点。

深度子空间聚类(DSC-l1):基于l1正则化的构架。

深度子空间聚类(DSC-l2):基于l2正则化的构架。

上述几种算法均由作者提供的代码进行实验，为确保实验公平性，具体参数根据论文设置为最优，记录最优参数下结果进行对比，对比结果如表5所示。

由表5可知，所提算法相比一些子空间聚类算法在公开标准数据集上可以得出良好的聚类效果。在Extended Yale B数据集上ACC相比DSC-l1、DSC-l2算法高0.94%、0.28%；在ORL数据集上，ACC相比DSC-l1、DSC-l2算法高1.68%、1.43%；在COIL-20数据集上，ACC相比DSC-l1、DSC-l2算法高1.18%、0.55%。这说明在编码器部分使用混合函数和系数α将一对输入进行线性插值，得到的新混合输出可以在自表达层学习更好的特征表示，使得预训练过程更加缜密，提高了模型的泛化能力；并且在重构数据集上引入鉴别器，使重构的数据与难分类的样本更易分类，有效分离个体聚簇。

表5 不同算法在三个数据集上的实验结果对比

在所提算法中，平衡参数λ1、λ2和λ3的取值对聚类结果的影响较大。为讨论 3个参数对所提算法的影响，实验采用固定其二、改变其一来观察ACC和NMI的变化。实验结果见图4～图6。在Extended Yale B数据集上，ACC和NMI在λ1和λ2取值区间中起伏较大，在λ3取值为{6，6.5，7}时变化相对较小、基本平稳，最佳值设置为λ1=1.00、λ2=10.00、λ3=6.30；在ORL数据集上，ACC和NMI均在λ1小于0.1、λ2小于0.5、λ3大于1的取值范围内聚类性能显著，最佳值设置为λ1=10-3、λ2=0.1、λ3=1.1；在COIL20数据集上，在λ1取值为{10-3，10-2，10-1，100},λ2取值为{0.5，1，1.5，2}，λ3取值为{0.1，0.5，1}时，ACC值的变化相对较小，NMI值的变化基本平稳，最佳值设置为λ1=1.00、λ2=1.5、λ3=0.4。从图4～图6可知，噪声对不同的数据集影响程度不同，因此，平衡参数的最佳值也不相同。但在合适的取值区间上，提出的融合线性插值和对抗性学习的深度子空间聚类算法体现出了较好的稳定性。

图4 Extended Yale B数据集中不同λ1、λ2、λ3上的ACC和NMI变化曲线

图5 ORL数据集中不同λ1、λ2、λ3上的ACC和NMI变化曲线

图6 COIL20数据集中不同λ1、λ2、λ3上的ACC和NMI变化曲线

此外，邻接矩阵的学习方法与深度子空间聚类相同，由于近邻数不同，很大程度上影响了聚类准确度，因此，为了考虑k值变化对算法的影响，通过将k区间设置为(2,50)来显示不同聚类结果。通过图7可以清晰地看出k在不同数据集上最优值。在Extended Yale B数据集上，当k=14时，聚类准确率达到最优；在ORL数据集上，当k=15时，聚类准确率达到最优；在COIL20数据集上，当k=17时，聚类准确率达到最优。由图7可知，在三个数据集上k值均在(10,30)区间比其他区间的聚类效果好，这说明所提算法在簇数较多时聚类精度较高，同时验证了算法对分离个体簇具有有效性。

图7 在Extended Yale B、ORL、COIL20数据集上不同k值聚类结果

4 结束语

该文提出了一种融合线性插值和对抗性学习的深度子空间聚类方法(DSC-IA)，该方法有以下创新点：其一，在编码器部分使用混合函数和α系数线性插值两个隐表示；其二，通过对抗性学习，在新的混合重构集上训练一个鉴别器来预测用于混合函数的α系数。在三个常用基准数据集上的实验结果证明了DSC-IA相对于其他算法的优越性，并验证了本模型设计的优势。算法在聚类精度方面，比其他的子空间聚类解决方案有显著改进。