基于权重融合法的跨海桥梁部位及部件权重体系分析
2023-03-27夏子立景强高文博刘祖锋张阳
夏子立,景强,高文博,刘祖锋,张阳
(1.港珠澳大桥管理局,珠海 519000; 2.华南理工大学土木与交通学院,广州 510640; 3.长安大学公路学院,西安 710064)
随着中国桥梁建造技术的突破以及经济快速发展的需要,越来越多跨海大桥工程得以建设实施,自1991年中国第一座跨海大桥建成,至2018年10月港珠澳大桥建成通车,中国拟在建及建成的跨海大桥已接近百座[1-2]。目前中国的桥梁建设已逐步由“重建轻养”转变为“建养并重”,由于跨海桥梁具备工程规模大、结构形式复杂且所处自然环境恶劣等特点,其对于桥梁维养工作提出了更高要求。
桥梁技术状况评定是桥梁维养工作开展的重要依据,对于不同技术状况等级,桥梁管养人员将做出对应的养护决策,因此准确评定桥梁的技术状况等级尤为重要。目前,中国已构建了较为完善的桥梁技术状况评定标准体系,主要依据《公路桥梁技术状况评定标准》(JTG/T H21—2011)[3]、《城市桥梁养护技术规范》(CJJ 99—2017)[4]等标准及规范开展桥梁技术评定工作。桥梁部位及部件权重是技术状况评定的关键参数,权重的合理分配直接影响桥梁技术状况等级,贴近工程实际的技术状况评定权重体系可更准确地反映桥梁的实际服役状态,在此基础上桥梁管养人员方可开展更具针对性的维养措施。《公路桥梁技术状况评定标准》(JTG/T H21—2011)和《城市桥梁养护技术规范》(CJJ 99—2017)均按照不同结构形式赋予桥梁部位及部件不同的权重,并考虑了未出现或者缺失部件的二次权重分;虽然评定体系及方法已较为完善,但在实际的评定工作中,依然存在部件权重与桥梁实际的匹配度不足的情况[5-6]。关于桥梁部件权重研究,国内学者采用层次分析法(analytic hierarchy process,AHP)对斜拉桥[7]、钢桁架桥[8]、钢管混凝土拱桥[9]以及石拱桥[10]等桥型的部件权重进行了分析研究,但传统的层次分析法主要采用专家打分进行指标量化,存在主观性较强、结果偏差较大等问题。
《公路桥梁技术状况评定标准》(JTG/T H21—2011)指出,对于跨江、海等特大型桥梁,可针对其自身特点,遵循标准原则,构建具备针对性的评定体系。现以港珠澳大桥青州航道桥为案例,收集熟悉该桥梁设计、施工、维养以及检测等方面专家的评分数据,采用层次分析及专家群组分析等方法分析专家评分数据形成桥梁部位及部件“主观权重”,采用熵权法分析桥梁结构健康监测数据得出桥梁部位及部件的“客观权重”,通过权重融合,以期形成兼顾专家打分及监测数据的“权重体系”。
1 综合分析体系构建
层次分析法是美国运筹学教授T.L.Satty 在20世纪80年代提出的一种定性和定量相结合的、系统化、层次化的分析方法[11],其主要的分析过程为将目标层分解为多个准则层,再细分为多个要素,根据各要素的重要程度对比计算出要素权重。单一层次分析法受专家个人经验、意见的主观影响,且受标度规则的影响较大。对此,吕跃进等[12]、骆正清等[13]提出用群体判断方法和对该不足进行改进。熵权法是一种客观赋权的理论方法,其广泛应用于各行业的技术研究,在桥梁耐久性评价[14]、桥梁加固方案优选[15]、桥梁检测及监测[16-17]等方面均得到应用;按照信息论基本原理,信息是系统有序程度的一个度量,熵是系统无序程度的一个度量,根据信息熵的定义,可用熵值来判断某个指标的离散程度,其信息熵值越小,指标的离散程度越大,该指标对综合评价的影响就越大[18-19]。因此,可利用信息熵计算各个指标的权重,为多指标综合评价提供依据。熵权法不能反映专家的知识和经验,其仅依赖于数据本身的离散性,得出客观的权重值。
层次分析法考虑了专家的知识和经验,以及决策者的意向和偏好,虽然指标权重的排序往往具有较高的合理性,但无法克服主观随意性较大的缺陷;而熵权法仅依据数据得出分析对象的客观权重,不能反映专家经验及决策者的意见。综合两种方法的优缺点,把群组层次分析法和熵权法的结果相结合,得到综合考虑主客观因素的指标权重。图1展示了权重综合分析流程。
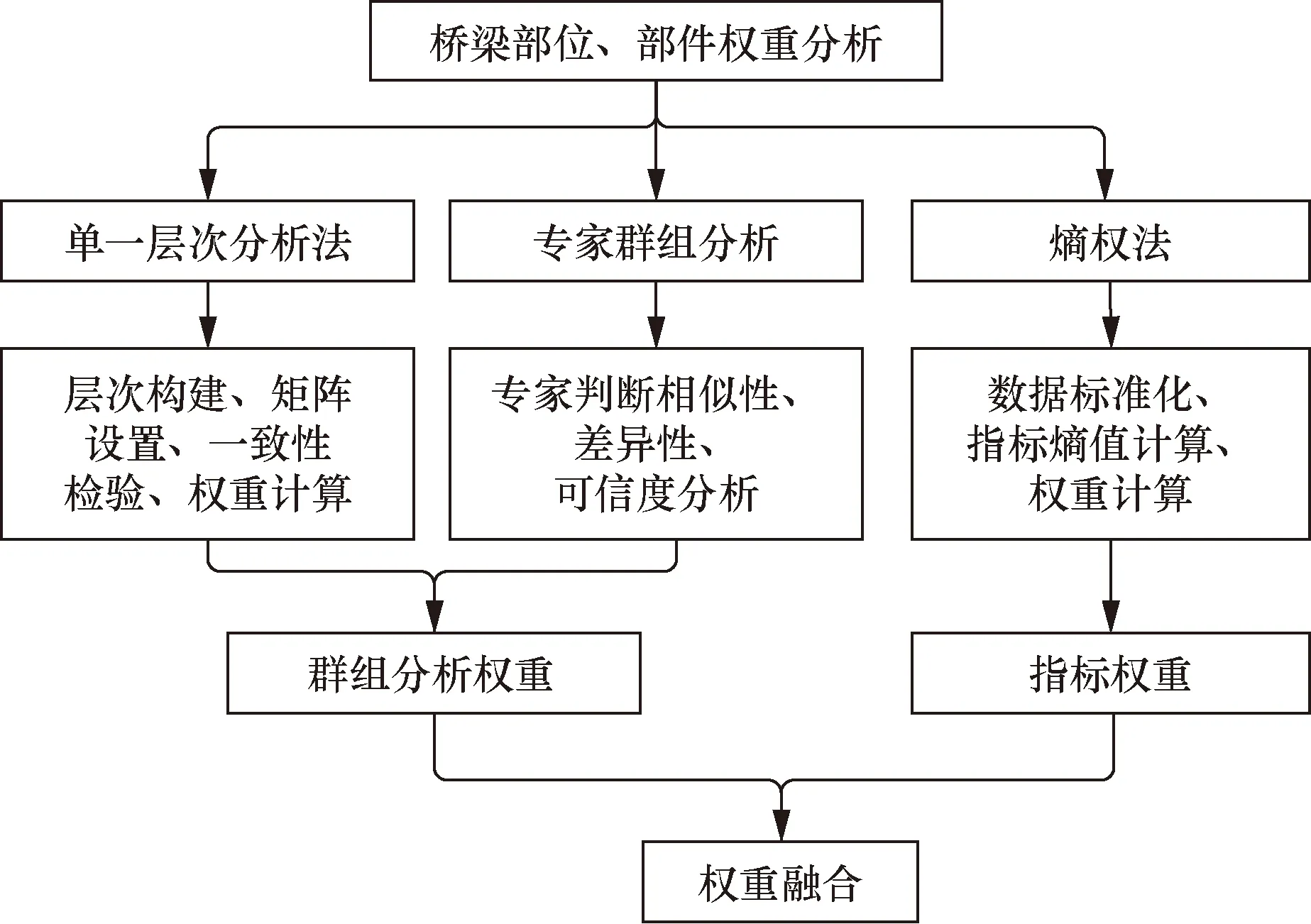
图1 权重综合分析流程Fig.1 Comprehensive weight analysis process
1.1 单一层次分析法分析过程
1.1.1 矩阵设置
比较n个因素y=(y1,y2,…,yn)对目标z的影响,每次取两个因素yi和yj,用aij表示yi与yj对z的影响程度之比,n个被比较的元素构成一个两两比较的判断矩阵A=(aij)n×n,表达式为
(1)
确定aij的取值采用9标度法[10],判断矩阵标度如表1所示。
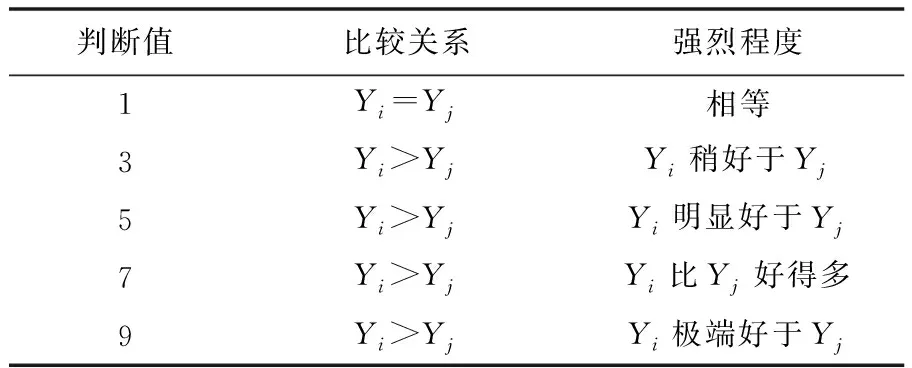
表1 判断矩阵标度Table 1 Judgment matrix scale
1.1.2 矩阵一致性检验
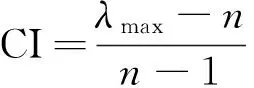
(2)
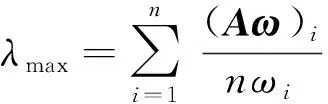
(3)
式中:CI为一致性指标;λmax为最大特征根;ω为最大特征根对应的特征向量;n为判断矩阵阶数;ωi为第i个元素的权重。
1.1.3 随机平均一致性指标
随机平均一致性指标RI由重复进行多次的随机判断矩阵特征值计算后取算术平均得到。表2为1~8阶指标取值。

表2 随机一致性指标Table 2 Random consistency index
1.1.4 一致性相对指标

(4)
当CR<0.1时,认为判断矩阵通过一致性检验;当CR>0.1时,认为判断矩阵不通过一致性检验,需要对该判断矩阵进行重新修正。当式(3)对判断矩阵所有元素都成立时,则称该判断矩阵为一致性矩阵。
1.1.5 要素权重计算
对于一致性判断矩阵,每一列归一化后就是相应的权重。
Aω=λmaxω
(5)

(6)
式中:A为判断矩阵;ω为最大特征根对应的特征向量,将向量ω进行归一化处理,向量元素即为矩阵中的元素排序权重;ωi为第i个元素的权重。
1.2 专家群组分析过程
1.2.1 专家判断的相似性分析
通过计算向量夹角来反映专家评定结果的相似性,相似程度随夹角的变小而增大[20]。


(7)
式(7)中:η为相似性系数;θ为向量α、β的夹角;ai为向量α第i个向量元素;bi为向量β中第i个向量元素。
将n个专家构造的判别矩阵变为行向量形式,即[α1,α2,…,αn],令ηij表示αi和αj的空间夹角的余弦,得到几何相似系数ηi,该系数表示第i个专家评定结果的可信度,表达式为

(8)
对ηi进行归一化处理,用ui表示该专家与其他专家的相似度,即
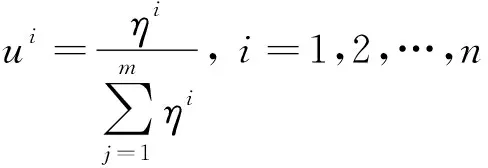
(9)
1.2.2 专家判断的差异性分析
令α1,α2,…,αn为第k位专家对n个判断指标构建的判断矩阵对应的行向量,ei为所有专家对第i个评定指标评判的均值,则

(10)
令σki=|αki-ei|,则有
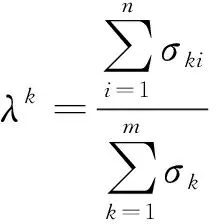
(11)
式(11)中:λk为差异度,即第k个专家的差值与所有专家总差值的比值。λk增大则信度降低。
1.2.3 群组判断可信度分析
将差异性与相似性作为可信度计算变量,则第k个专家群组可信度为
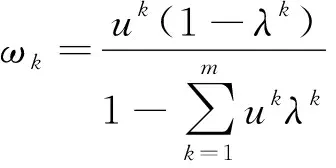
(12)
1.2.4 群组分析权重
每位专家在单一层次分析法中已经得到该专家给出的权重向量wk0,结合专家可信度,得到综合的最终群组层次分析法下的权重为
K={k1,k2,…,kn}
(13)
式(13)中:K为指标1到指标n的群组分析得出的权重;ωi为第i个专家群组可信度;μij为第i个专家对于指标j的层次分析法确定权重。
1.3 熵权法分析过程
1.3.1 数据标准化处理
为防止各指标量纲不统一,量级不一致,需要对原始数据进行标准化处理,即

(14)
式(14)中:Yij为原始数据标准化的结果,i、j分别为指标和样本编号(i= 1,2,…,n;j= 1,2,…,m);Xij为未处理的原始数据;Xi为所有样本指标i的向量。
1.3.2 权重计算
(1)计算第i个因素下第j个样本值的比重Pij。
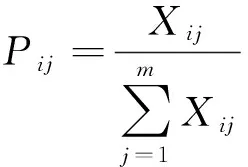
(15)
(2)计算第i个因素的熵值ei。
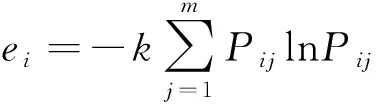
(16)
若取k=1/lnm,则0≤ei≤1。
(3)计算第i个因素的差异系数gi。
gi=1-ei
(17)
对于给定的ei越大,因素评价值的差异性越小,则因素在综合评价中所起的作用越小。则当因素gi越大时,因素越重要。
(4)权重确定。

(18)
式(18)中:wi即为熵权法确定的权重。
1.4 主客观权重融合
根据层次分析法、熵权法得到对应的指标权重值,将两种方法得到的权重融合,得到综合考虑主客观因素的指标权重[21-23],表达式为
wi=αiη+βi(1-η)
(19)
式(19)中:αi、βi分别为评价的主、客观权重;η为重要性系数(0≤η≤1),表示主客观权重在融合权重中的重要程度比,一般而言,取η=0.6[24-25]。
2 实践案例
2.1 工程概况
港珠澳大桥是连接粤港澳三地的大型跨海通道,是国家高速公路网中珠江三角洲地区环线的组成部分和跨越伶仃洋海域的关键性工程,大桥于2018年10月通车运营[26]。青州航道桥是港珠澳大桥3座通航孔斜拉桥之一,其采用双塔、双索面钢箱梁斜拉桥,全长1 150 m,桥跨布置为(110+236+458+236+110)m,边跨设置辅助墩,桥型布置如图2所示,航拍图如图3所示。

图2 青州航道桥桥型布置Fig.2 Qingzhou Bridge bridge style layout

图3 青州航道桥航拍图Fig.3 Aerial shot of Qingzhou Bridge
2.2 桥梁结构解析及专家打分体系构建
参照《公路桥梁技术状况评定标准》(JTG/T H21—2011),按照“桥梁-部位-部件”的层次对青州航道桥进行结构解析,如图4所示。对照标准关于斜拉桥构件划分形式,青州航道桥不包含翼墙、护坡、桥台以及调治构造物等部件。
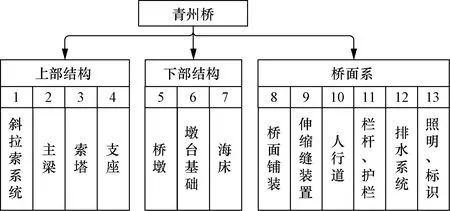
图4 青州航道桥结构解析Fig.4 Structural analysis of Qingzhou Bridge
按照上述划分层次,设计专家调研打分表格,以桥梁上部结构为例,如表3所示。专家按照表1的打分规则,两两对比部件之间的重要程度并生成打分数据。

表3 桥梁上部结构部件专家打分表Table 3 Expert grading table for bridge superstructure components
2.3 专家打分数据处理
2.3.1 数据处理过程
调研收集熟悉港珠澳大桥主体工程设计、施工、维养、检测以及科研等方面共36位专家的打分数据,按照前述的单一层次分析方法以及专家群组分析计算桥梁部位及部件权重。以某专家反馈的打分数据为例(表4),计算过程如下。

表4 某专家打分数据Table 4 Expert rating data
(1)单一层次分析。按照1.1节的计算公式得出CI=0.066 0,λmax=4.198 1,n=4,RI=0.89,CR=0.074 2<0.1;矩阵的一致性检验通过。对矩阵每一列归一化后得出斜拉索系统、主梁、索塔、支座的权重分别为0.508 3、0.265 3、0.151 2、0.075 2。
(2)专家群组分析。将所有专家的数据按照上述步骤分别计算,得到共36组权重数据。以前10位专家对上部结构位的打分数据为例,按照1.2节专家群组分析方法计算专家打分的相似性、差异性及可信度,如表5、表6所示。
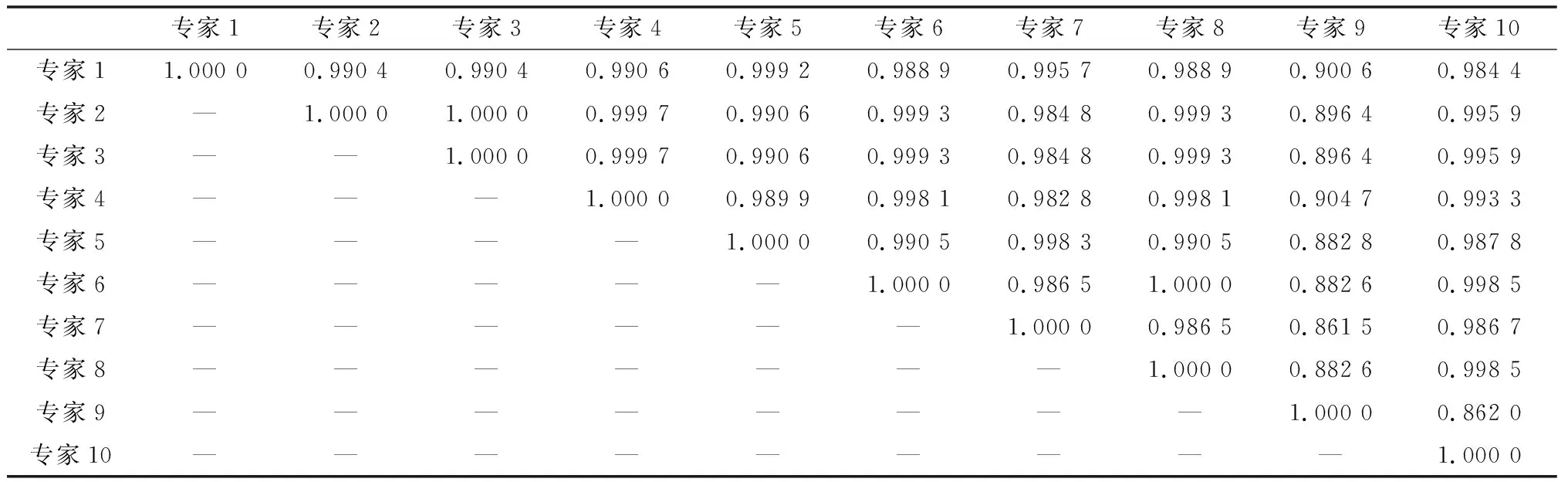
表5 专家打分相似性分析Table 5 Expert score similarity analysis

表6 专家打分差异性与可信度分析Table 6 Expert scoring difference and credibility analysis
(3)权重计算。基于专家单一层次分析及专家群组可信度分析,得出斜拉索系统、主梁、索塔、支座的权重分别为0.521 7、0.223 5、0.185 7、0.069 1。
2.3.2 桥梁部位权重计算结果
36位专家的打分数据进均符合一致性检验,各位专家的桥梁部位打分结果如表7所示,专家打分数据的分布区间如图5所示。最终得出桥梁上部结构、下部结构及桥面系的权重值分别为0.448 4、0.416 9、0.134 7。

图5 专家打分数据分布区间Fig.5 Expert scoring data distribution interval

表7 桥梁部位权重分析结果Table 7 Weight analysis results of bridge parts
2.3.3 桥梁部件权重计算
按照前述的计算方式,对36位专家的打分数据进行计算分析,得出桥梁各部件的权重如下。
(1)上部结构。斜拉索系统、主梁、索塔、支座的权重值分别为0.466 8、0.242 5、0.202 9、0.087 8。
(2)下部结构。桥墩、墩台基础、海床的权重值分别为0.450 1、0.391 0、0.158 9。
(3)桥面系。桥面铺装、伸缩缝装置、人行道、栏杆及护栏、排水系统、照明与标志的权重值分别为0.314 5、0.314 9、0.081 5、0.114 2、0.104 8、0.070 0。
2.4 熵权法数据处理
熵权法通过原始数据所包含的信息量来确定研究目标的权重,需要保证数据的连续性及与实际情况的关联性,以保障数据可反映桥梁监测的实际状况。在桥梁体系中,常态动态响应反映了桥梁的基本参数情况,如桥梁健康状态下响应在时域上分布较为均匀,反之损坏后则桥梁响应分布波动较大。
青州航道桥部分传感器布设如图6所示,大桥稳定、连续的监测数据可满足熵权法的分析需求。为介绍熵权法确定权重的过程,选用大桥某时段共180 d的上部结构(塔顶)加速度传感器、下部结构(墩台)加速度传感器以及桥面系(伸缩缝)位移传感器的监测数据,该数据的混乱程度即反映其所包含的信息量,通过熵权法确定的桥梁上部结构、下部结构以及桥面系3个部位的权重。
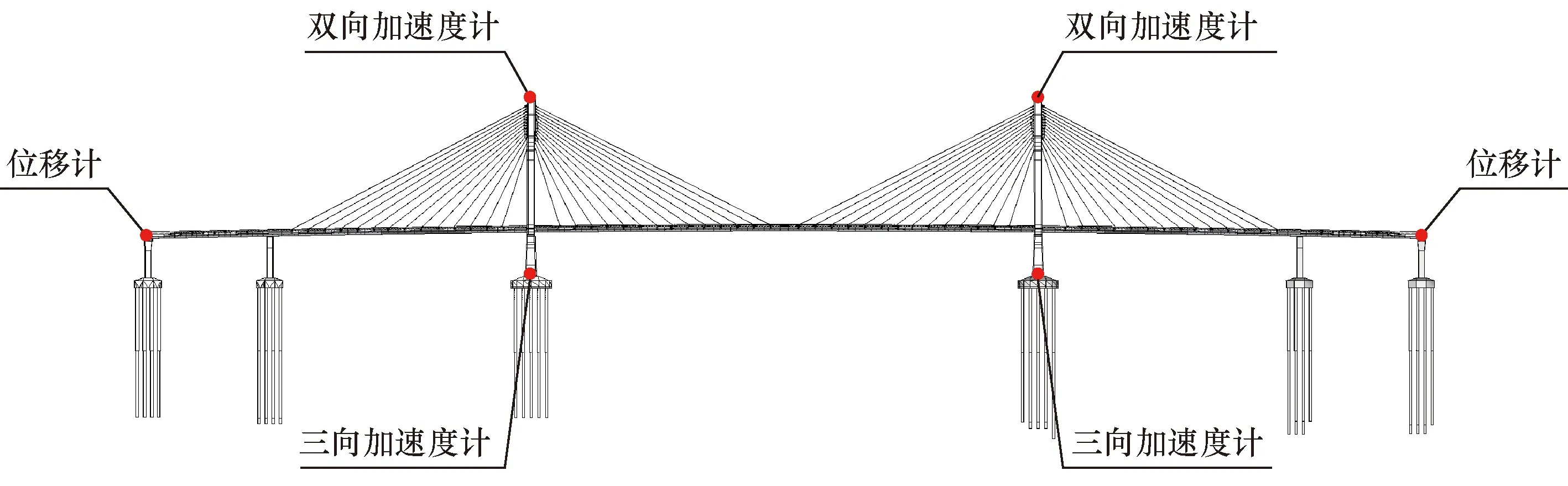
图6 青州航道桥健康监测传感器布置图(部分传感器)Fig.6 Qingzhou Bridge health monitoring sensor layout (some sensors)
2.4.1 数据标准化处理
监测数据难免出现异常值、漂移等现象,在数据标准化之前先进行数据的预处理;此外,上部与下部结构均采用加速度振动信号,而桥面系采用的是位移信号,其中包含了车辆引起的快变信号和温度引起的慢变信号;车辆引起的梁端累计位移是伸缩缝寿命的重要指标。因此,为了保证三者之间相同物理信息,对伸缩缝位移信号进行去温度效应处理[27-29]。将预处理后的数据按照式(14)进行标准化处理,处理结果如图7所示。按照式(15)进行数据比重值计算,计算结果如图8所示。

图7 监测数据标准化处理Fig.7 Standardized processing of monitoring data

图8 监测数据比重Fig.8 Specific gravity of monitoring data
2.4.2 数据权重计算及分析
采用熵权法分析得到上部结构、下部结构和桥面系监测数据的熵值为0.935 1、0.947 4、0.971 4。3个部位的监测数据熵值接近于1,可得出以下结论。
(1)监测数据的合理性和可靠性,异常数据量少,不会影响整个数据质量。
(2)数据波动不大,由于车流量较少,结构响应变化幅值较小。
(3)上部结构由于承受桥面荷载和风荷载,因此熵值最小;下部结构响应主要来源于地脉动或地震,正常运营阶段下部结构响应较为平稳,当监测到地震时,响应会出现明显峰值,因此熵值大于上部结构;桥面系由于车流量小引起的纵向振动较小,因此熵值最大。
基于监测数据的熵值,得出桥梁上部结构、下部结构和桥面系对应的权重值为0.444 2、0.360 0、0.195 8。需要指出的是熵权值法过分依赖于数据质量和长度,此外不同的数据标准化处理方法也会在一定程度上影响结果。
2.5 权重融合及权重值对比分析
通过群组层次分析法和熵权法得到桥梁部位主观权重和客观权重,采用权重融合方法得到桥梁部位的融合权重,与《公路桥梁技术状况评定标准》(JTG/T H21—2011)对于斜拉桥的部位权重值进行对比,如表8所示。采用群组层次分析法分析得到上部结构比标准规定的权重稍大,桥面系的权重偏小,下部结构的权重偏差较小;采用熵权法分析得到的上部结构权重值比标准规定的权重稍大,下部结构、桥面系的权重基本一致;通过权重融合法得到的权重综合了层次分析法和熵权法得到的数据结果,与标准规定的权重相比,仍然是上部结构的权重偏大,桥面系的权重偏小,下部结构的权重基本一致。

表8 桥梁部位权重对比分析Table 8 Comparative analysis of weight of bridge parts
由于桥梁结构健康监测无法覆盖所有部件,如墩台基础、海床、人行道、护栏、排水系统等部件无监测数据,因此桥梁部件权重并未采用熵权法进行分析。通过群组层次分析法得到各个部件的主观权重,与《公路桥梁技术状况评定标准》(JTG/T H21—2011)对于斜拉桥部位权重进行对比,如表9所示。经分析对比可知,除下部结构-海床、桥面系-照明与标志、伸缩缝装置外,其他部件采用群组层次分析法得到权重和标准权重相比差别不大,专家群组对桥梁各部件的重要性判断基本一致。

表9 桥梁部件权重对比分析Table 9 Comparative analysis of weight of bridge components
3 结论
采用层次分析法、专家群组分析和熵权法构建桥梁部位及部件权重综合分析体系。以港珠澳大桥青州航道桥为分析对象得出其桥梁部位、部件权重值,对比现行桥梁技术状况评定标准给出权重体系,得到如下结论。
(1)以港珠澳大桥青州航道桥为案例,收集了多位熟悉该桥梁设计、建设及维养方面专家的打分数据,采用层次分析与专家群组分析相结合的方法分析专家评分数据形成桥梁部位及部件“主观权重”。与技术状况评定标准相比,采用群组分析方法得出的桥梁上部结构权重值偏大,桥面系的权重值偏小,下部结构的权重值基本一致;采用群组分析方法得出桥梁下部结构-海床、桥面系-照明与标识、伸缩缝装置权重值偏差稍大,其他部件的权重值与标准给出的权重值基本一致。
(2)基于港珠澳大桥青州航道桥结构健康监测数据,采用熵权法得出桥梁部位“客观权重”,与标准规定的部位权重相比,上部结构比标准规定的权重稍大,下部结构、桥面系的权重值基本一致。熵权法的使用需基于大量稳定性、持续性好的高质量监测数据,目前桥梁监测难以覆盖所有部件,因此对于部件的权重融合分析,还有待进一步研究。
(3)与标准规定的权重相比,通过权重融合法得到的桥梁上部结构的权重偏大,桥面系的权重偏小,下部结构的权重基本一致。通过权重融合,综合了层次分析法和熵权法得到的分析结果,更加贴近工程实际,可更合理地反映桥梁部位的实际权重,应用于实际的桥梁技术状况评定工作中可更准确地反映桥梁的服役状态。
(4)层次分析法考虑专家的知识和经验,专家群组分析可降低专家的打分主观随意性;熵权法基于数据本身的离散性,可得出的相对客观的权重结果。综合两种方法的优缺点,基于层次分析法和熵权法构建了桥梁部位及部件权重综合分析体系,通过权重融合法得出了综合考虑主客观因素的指标权重,可为桥梁技术状况评定结构权重体系构建提供参考。
