移动荷载作用下既有高速铁路路基拓宽计算分析

李丽华，康浩然，郑志刚，裴尧尧*，宋杨，李孜健

(1.湖北工业大学土木建筑与环境学院湖北省生态道路工程技术研究中心，武汉 430068； 2.河北水利电力学院河北省岩土工程安全与变形控制重点实验室，沧州 061000)

随着经济的发展，对铁路列车的数量和运载量要求不断增大，导致铁路荷载增大。

提高铁路线承载能力最经济有效的方法之一是扩建现有路基[1]。然而，在列车荷载作用下由于土的应力历史及压实度差异，新、旧路基之间容易出现不均匀沉降，进而出现裂缝导致失稳破坏。

为改善铁路路基加宽过程中出现的失稳问题，国内外学者进行了一系列研究。左坤等[2]依据工程实例对既有线加宽路基关键施工技术进行了改进。叶观宝等[3]、李立等[4]基于离心模型试验，研究了路基拓宽后新旧路基变形、地基土中孔压和土压力的变化规律。时瑾等[5]、袁堃等[6]和Yu等[7]利用实际工程案例建立了数值模型，分析了行车条件对既有线路基应力状态的影响关系以及参数敏感性。

土工加筋技术作为一种常用的不良路基处治手段也同样得到了应用和推广[8-9]。随着加筋结构的修建，加筋理论不断完善，加筋技术也日趋成熟。张玲等[10]利用有限元软件建立了土工加筋路堤三维数值模型，对移动荷载下土工加筋路堤的动应力和变形等变化规律进行了深入分析。Li等[11]通过现场测量过大孔隙压力和侧向土体位移，研究了将两组开放式预应力高强混凝土桩顶入现有公路路堤的影响。Kamash等[12]对既有路堤下加宽部分进行了模拟，建立了考虑既有路堤和加宽段地基土固结的力学和水力耦合数值模型。Lazorenko等[13]在此基础上，利用Plaxis2D有限元软件对3种加筋方案下的铁路路基拓宽时出现的问题进行了数值解。

国内对既有线高速铁路路堤加宽的研究目前仍然比较少，且主要停留在施工方法阶段，分析不够深入，考虑的影响因素较为单一，不具备设计方面的指导意义。相对于国内的研究，国外对既有线高速铁路路堤加宽的研究更偏向于设计层面，以工程实例结合数值模拟为主。但仍然存在如下一些问题。

(1)既有线高速铁路路堤加宽导致整体失稳是随着经济发展近些年才出现的现象，整体研究还是较少。

(2)为提高模型计算和分析的效率，很多研究都对三维既有高速铁路路基加宽问题进行二维简化，但忽略了边界条件等因素对计算结果的影响，且无法模拟三维稳定性问题。

(3)荷载仍以静载为主，但对于实际重载铁路，动载更应该被重视。

现结合某工程案例，建立既有高速铁路加宽路基的三维有限元模型，对加宽路基动态响应特性进行研究。分析在不同速度列车荷载作用下动力衰减特性。设置3种加筋方案，与无加筋路基最大沉降和横向变形进行对比。

1 有限元模型

1.1 几何尺寸及参数

依托中卫至兰州铁路ZLKZ-ZQSG7标段项目，参考铁路路基实际结构形式及《高速铁路设计规范》(TB 10621—2014)，建立高速铁路路基实尺数值仿真模型。拟分析的既有高速铁路加宽路基模型如图1所示，岩层主要由石灰岩构成，材料参数如表1所示。路基高7.0 m，坡度为1∶1.8，坡顶加宽长度为8.2 m，加宽部分上部设置1.2 m由砂土构成的排水保护层，放置土工布。路基与轨道间包括0.4 m的道砟层和0.2 m的底砟层。

图1 铁路加宽路基示意图Fig.1 Schematic diagram of the railway widening roadbed

采用Plaxis3D有限元软件进行模拟，建立了三维有限元模型，土工加筋材料、路面结构层及各层土材料本构模型及主要参数根据参考文献[13-14]和相关经验参数确定。考虑到材料特性，岩层采用霍克布朗模型，在霍克布朗模型中，将岩层视作一种脆性材料，一旦达到材料强度，就立即发生破坏，具体参数见表1。其他土料采用硬化土模型，硬化土模型考虑到了土体自身的压缩性，可以更好地反映土体卸载时的应力应变关系，具体参数见表2。其模型参数主要由固结试验和三轴试验获得，模型用到的土工合成材料为土工格栅和土工织物，均选用弹塑性本构模型，具体参数见表3。图2为构建的铁路加宽路基的三维模型。

表1 岩层材料参数Table 1 Rock material parameters

表2 路面结构及各层土材料参数Table 2 Pavement structure and material parameters for each layer of soil

表3 土工材料参数Table 3 Geotechnical material parameters

图2 铁路加宽路基的三维模型Fig.2 Three-dimensional model of the railway widening roadbed

1.2 边界条件和网格划分

为更好地模拟实际施工条件，观测路基变形，设置边界条件为：路基四周水平约束，底部固定约束，顶部自由约束。同时为吸收动力荷载所产生的回弹效应，动力边界为黏性，设置边界条件如表4所示。

表4 边界条件Table 4 Boundary conditions

为确保计算精度并兼顾计算效率，对加宽部分和新、旧路基连接段进行局部细化处理，共包括367 740个十节点单元。高速铁路加宽路基网格如图3所示。

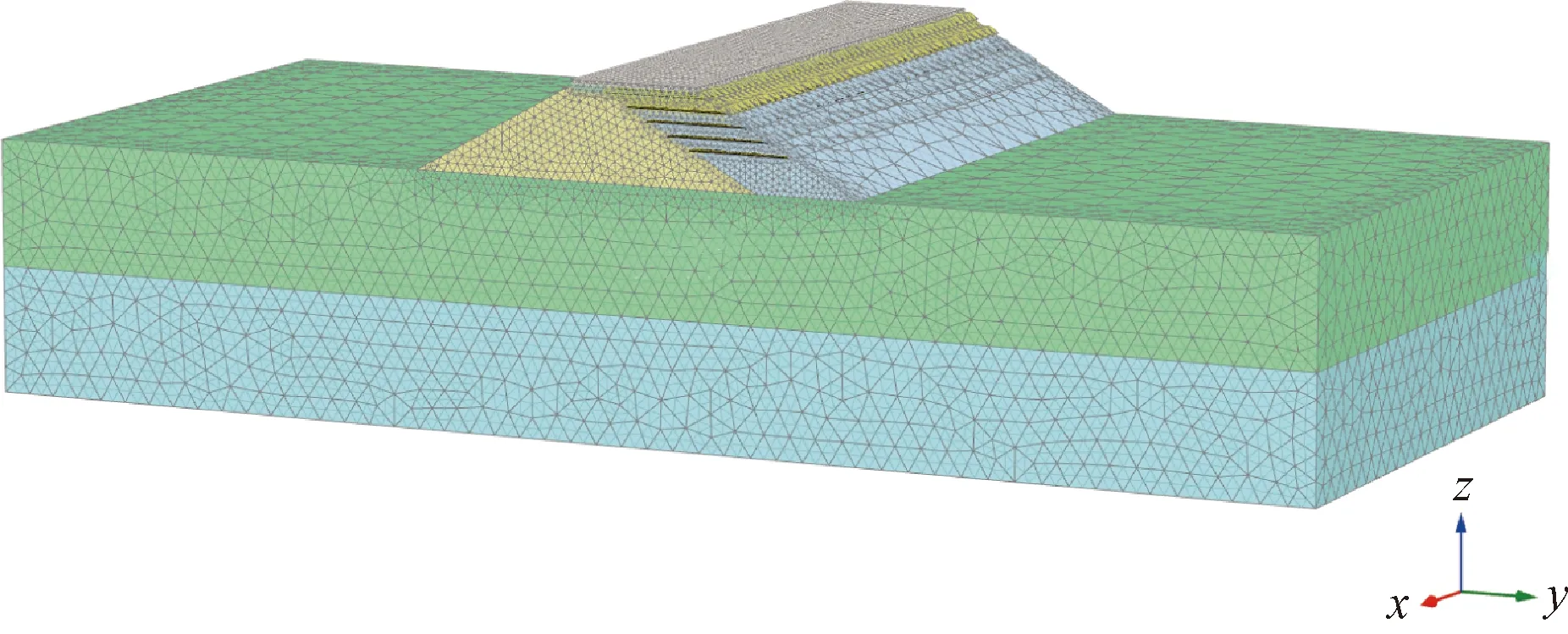
图3 高速铁路路基加宽路基网格Fig.3 High-speed railway roadbed widening roadbed grid

1.3 铁路列车荷载

轴向荷载计算均匀分布在轨木宽度上的等效垂直压力，定义为

(1)

式(1)中：Qvk为集中荷载；L为轴向荷载分布的纵向长度；B为铁路枕木宽度；αQ为铁路车辆的振动动态负荷因子，取1.3[15]。考虑250、275和300 kN 3种不同大小的列车荷载，等效均布荷载分别为75.2、82.6和90.3 kN/m2。

路基内部各结构层应力水平的确定，对高速铁路路基的设计至关重要。影响高速列车路基内部动力荷载的众多因素中以列车运行速度的影响尤为显著。目前，中国《铁路路基设计规范》[15]中提出了路基设计动应力幅值计算公式为

σdl=0.26P(1+αv)

(2)

式(2)中：时速 300～350 km/h时，α=0.003；时速 200～250 km/h时，α=0.004；P为机车车辆的静轴重(按中国客运专线标准活载)；(1+αv)为冲击系数，客运专线铁路最大冲击系数为1.9。

1.4 模型有效性验证

为验证所建立既有高速铁路加宽路基有限元模型的有效性，将使用该模型在上述3种列车荷载作用下计算的路基表面峰值竖向应力σy与Konshin的实验研究结果[16]和Lazaorenko利用Plaxis2D数值模拟结果[13]进行对比，对比结果如图4所示。

如图4所示，本文计算结果在Konshin试验研究结果区间内，说明既有高速铁路加宽路堤的三维有限元模型构建合理，利用Plaxis3D软件在正确使用边界条件、网格划分、几何图形、本构模型、参数和建模过程，可以模拟既有铁路加宽路基的实际承载情况。该模型与Lazaorenko使用的有限元二维模型输出结果相比趋势较为一致，路基表面峰值与列车荷载之间均呈现出线性正相关。同时，三维模型输出结果较二维模型相比偏小，这是由于平面应变模型没有考虑到路基纵向边界条件等问题，导致变形仅发生在平面内，容易产生较大的应力。虽然将三维问题进行二维简化处理可以提高计算和分析效率，但忽略了边界条件等因素对计算结果的影响，且无法模拟三维稳定性等问题。

图4 不同荷载下路基表面峰值竖向应力对比Fig.4 Comparison of peak vertical stresses on the roadbed surface under different loads

2 路基动态响应特性

2.1 时程分析

为模拟铁路动荷载作用，将50 m的均布荷载等分成25个长度2 m的均布荷载，使用25个随时间变化的函数控制乘子变化，以达到模拟铁路列车运动的目的。

列车纵向长度设置为100 m，速度为300 km/h，列车通过模型全程耗费1.8 s。在0.6 s时刻路基表面开始被列车荷载覆盖，1.2 s时刻之后列车尾部驶入路基，1.8 s时刻驶离。

计算分为两步：第一步为初始阶段，产生包括由土壤自重引起的初始应力，然后将由该应力引起的变形归零；第二步为动力计算，根据设置好的乘子进行时间间隔为0.01 s的动应力迭代计算。

图5展示了在不同时刻既有高速铁路加宽路基表面处的增量位移。可以看出，在0.3 s时刻，列车接近到达该模型的中间位置，增量位移主要发生在列车到达处即模型中部附近；在0.6 s时刻，列车恰好达到模型尾部，增量位移集中在模型尾部位置，而此时开始列车荷载覆盖整个模型，这一过程持续到1.2 s时刻。在此期间，路基的增量位移相对来说数值较小且比较稳定。从1.2 s时刻开始，列车尾部进入模型直到1.8 s时刻全部驶离，在此期间模型的增量位移主要发生在列车尾部附近，随着列车的驶离，既有高速铁路加宽路基在之前发生的变形有一定恢复，且增量位移集中处与列车尾部驶离位置接近，说明变形恢复较为迅速且大部分变形恢复发生在荷载变化时段；此外，在列车动荷载作用下，变形不仅仅发生在荷载正下方的路基上，路基两侧的坡面上也伴随着变形发生，且靠近加宽路基一侧的坡面变形更明显，相对整体而言，加宽路基部分更容易发生过大的变形而导致失稳破坏。

图5 既有高速铁路路基在0.3、0.6、0.9、1.2、1.5、1.8 s时刻增量位移云图Fig.5 Incremental displacement clouds of existing high-speed railway roadbed at 0.3, 0.6, 0.9, 1.2, 1.5 and 1.8 s moments

2.2 动应力分析

取路基表面点(30，56，7.6)输出应力，该点处在荷载作用面下有一定代表性，得到路基表面动应力时程曲线，如图6所示。

图6 路基表面动应力时程曲线Fig.6 Time course curve of dynamic stresses on the roadbed surface

可以看出，该点应力在0.4 s时刻开始产生急剧增长，1.0 s增长速度变缓，在1.6 s时达到峰值接近160 kPa然后骤降到初始应力大小。相较于列车运动，路基表面应力变化并不及时，有一定的滞后性，在0.6～1.2 s阶段路基表面纵向被列车荷载完全覆盖，此时的外部荷载最大，1.2 s之后列车开始逐渐驶离，而此时路基表面应力仍未达到峰值。这是由于过程开始，在列车荷载作用下，路基发生沉降和横向变形，没有处于较为稳定的状态，应力没有完全传递，在经过一段时间之后，路基变形稳定，外部列车荷载传递到路基产生应力，并随之变化。

相较于列车静载而言，列车动荷载产生的路基表面峰值应力更大，其峰值应力增加53.84%。这是由于列车行驶时，不仅仅是荷载的施加，还伴随着轨道不平顺等引起的震动和摩擦效应，导致其更容易发生失稳破坏。

2.3 路基沉降与横向变形

列车动载作用下铁路路基不同高度处的沉降如图7所示。最大沉降发生的高度为7.0 m即道砟层和底砟层下的路基黏土位置，这是由于在最上层的道砟层和之后的底砟层材料之间存在空隙，且其材料有较好的振动和能量吸收性能。在大约0.3 s时刻之后沉降开始增加，1.5 s时刻达到峰值，最大值为27 mm，之后有一段变形恢复，最大值为23 mm。路基沉降与路基高度总体上呈现出正相关趋势，随着高度的降低，沉降减少。这是因为由列车引起的路基变形，开始主要是竖向位移及沉降，在向下传递的过程中并没有竖向传递而是向四周扩散了一部分，引起了横向变形，导致随着高度的降低，沉降减少。

图7 列车动载作用下铁路路基不同高度处的沉降Fig.7 Settlement of railway foundations at different heights under dynamic train loads

图8展示了在列车动荷载作用下铁路路基加宽一侧的坡面横向变形。总体而言，路基坡面的横向变形随列车的运动响应较快，0.2 s时开始发生，在1.2 s时刻左右变形基本已经稳定。与沉降不同，铁路路基坡面发生的横向变形并没有随列车的驶离而恢复，铁路路基坡面的横向变形几乎不可逆。最大变形发生在5 m附近，坡脚变形最小，其次是坡顶，铁路路基坡面的横向变形主要发生在路基中上部位置。

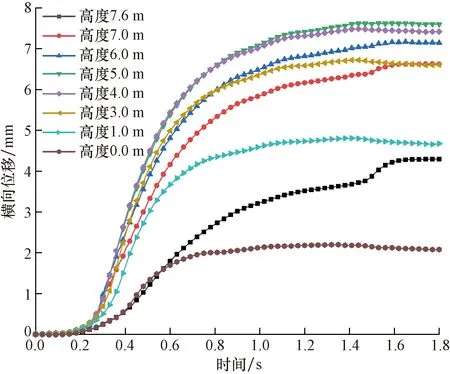
图8 列车动载作用下铁路路基坡面的横向变形Fig.8 Lateral deformation of the slope of a railway foundation under dynamic train load

2.4 动应力衰减

以路基表面处的动应力作为基准值，定义路基动应力衰减系数为各深度处的动态土压力与基准值的比值，对不同速度下既有高速铁路加宽路基的动力衰减规律进行研究。

图9展示了不同列车速度下的动应力衰减系数。可见在不同速度的列车荷载作用下动应力衰减规律基本一致，在距离路基顶面深度0～3 m内衰减速度较快，在距离路基顶面深度5 m往下衰减基本完成相对稳定。

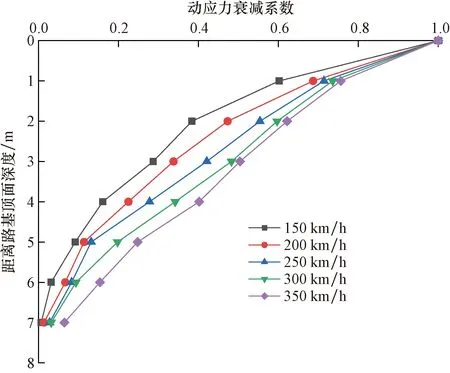
图9 不同列车速度下的动应力衰减系数Fig.9 Dynamic stress decay coefficient at different train speeds

动应力衰减系数与列车速度成反比，列车速度越低，前期动应力衰减速度越迅速，后期则基本保持一致。这是由于高速行驶的列车产生了更大的振动和能量，道砟层和底砟层的动能吸收作用被抵消，导致其影响范围更广、对土体产生更大的破坏。

3 土工合成材料作用

3.1 加筋方案设计

提高铁路承载能力最有效和经济的方法之一是扩建现有路基，尤其是路堤部分。然而，这仍然面临较多困难。

(1)扩建现有路堤的同时要保证原有路堤正常运作。

(2)由于时间影响，原有路堤经历了长时间风化沉降，新旧路堤之间结合存在困难，容易出现不均匀沉降而出现裂缝。

(3)若考虑加固，只能对扩建路堤部分进行加固，原有路堤部分不参与到整体加固。

根据以上研究，发现在列车移动荷载作用下，既有高速铁路加宽路基变形主要集中在上部且靠近加宽一侧，因此采用了3种加筋方案设计并与无加筋路基进行对比。

原模型在加宽路基上部设置主要由排水砂土构建的保护层，保护层与加宽路基之间设置排水层，中间加一层土工织物。方案一是在原模型基础上，在土工织物界面放置一层土工格栅。方案二在方案一基础上，以竖向间距1 m向上再放置两层土工格栅。方案三在方案二的基础上，以竖向间距1 m向下再放置两层土工格栅。

加筋材料和加筋层数以及对应加筋间距如表5所示。

表5 加筋方案Table 5 Reinforcement options

3.2 加宽路基变形特性

图10为在对不同加筋方案下的路基和无加筋路基进行路基最大沉降规律分析。可以看出，无加筋路基随列车荷载的增大，沉降呈现线性增长。通过土工材料加筋方式，对新加宽路基沉降有一定限制作用。

图10 不同列车荷载下路基最大沉降Fig.10 Maximum settlement of the roadbed under different train loads

在250 kN列车荷载下，相较于无加筋路基，其他3种方案加筋效果明显，方案二和方案三沉降减少幅度最大且接近。在275 kN列车荷载下，加筋效果更加明显，无加筋路基的沉降增长远远大于其他3种。随着列车荷载增加，方案一、方案二最大沉降增长速度先后开始提高，而方案三则较为稳定，在高列车荷载作用下加筋效果最明显。这说明加宽路基加筋存在一个“阈值”，在低列车荷载作用下，筋材没有达到这个阈值，筋材易与土体产生复合效应，加筋效果明显，随着列车荷载的增加，方案一、方案二先后达到阈值，沉降增长接近于无加筋路基。而方案三没有达到阈值，对沉降抑制效果最优，沉降增长较少。

300 kN为正常使用状态下列车的最大荷载，研究了在300 kN列车荷载作用下时速300 km/h加宽路基坡面横向变形随高度变化情况，如图11所示。

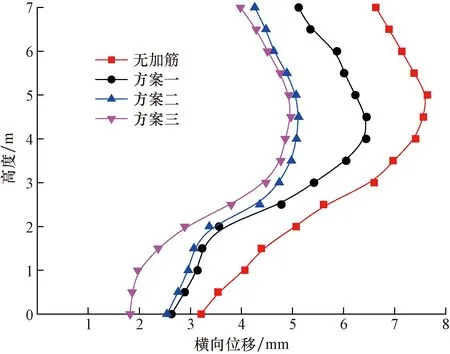
图11 不同加筋方式下加宽路基坡面的横向变形Fig.11 Transverse deformation of widened road base slopes with different reinforcement methods

可以看出，在300 kN列车荷载作用下土工格栅加筋效果明显，相对于无加筋路基，横向位移最大减少40.5%，且加格栅后坡面横向位移较为平滑，突变较少，这可能是由于土工格栅改善了土体结构，使之成为一种筋土复合体，提升了整体变形能力。而方案二和方案三坡脚横向位移差距略大，其他地方均较为接近，因此，结合不同加筋方案下既有高速铁路加宽路基的最大沉降，可以说明在正常列车荷载作用下，方案二既有明显的加筋效果又节省了材料，较为优选。

3.3 筋材应变

图12展示了300 kN列车荷载作用下方案三土工格栅中部位置处的应变随动力时间变化情况。可以看出，应变最大的为最上层格栅，格栅应变与所在高程呈现负相关，格栅埋置越深，应变越小。此外，虽然通过五层格栅进行路基加筋，但主要由上三层格栅发挥作用，下三层应变较小，未能充分发挥性能。因此，综合经济效益，在路基中上层进行三层加筋较为合适。

图12 筋材应变随时间变化情况Fig.12 Strain of the tendons as a function of time

4 结论

利用Plaxis3D有限元软件对某铁路路基加宽工程进行数值仿真，利用实际试验数据和前人二维模拟结果验证了三维模型的合理性。在此基础上，使用25个随时间变化的函数控制乘子变化，模拟铁路移动荷载进行动力计算，对既有高速铁路加宽路基动态响应特性进行研究。同时，考虑不同土工格栅加筋方案和无加筋路基进行对比分析，得到路基最大沉降、横向变形等分析结果。

(1)在列车动荷载作用下，变形不仅发生在荷载正下方路基上，路基两侧坡面上也伴随变形发生，且靠近加宽路基一侧坡面变形更明显，相对整体而言，加宽路基处更容易发生过大变形而导致失稳破坏。

(2)相较于列车运动，路基表面应力变化并不及时，有一定滞后性。相较于列车静载，列车动荷载产生的路基表面峰值应力更大，其峰值应力增加53.84%。动应力衰减系数与列车速度成反比，列车速度越低，前期动应力衰减速度越迅速，后期则基本保持一致。

(3)路基沉降与路基高度总体上呈现出正相关趋势，随高度的降低，沉降减少。路基坡面的横向变形随列车的运动响应较快，最大横向变形发生在路基上部。与沉降不同，铁路路基坡面发生的横向变形没有随列车驶离进行弹性恢复，铁路路基坡面的横向变形几乎不可逆。

(4)利用土工格栅对既有高速铁路加宽路基加筋，可以显著改善路基的变形特性，随着加筋层数增加改善效果越明显，结合经济效益以及筋材应变情况，在中上部3层进行加筋效果较好。