量化参数失配下基于事件触发的量化反馈滑模控制

陈志鹏，郑柏超,2*，赖琛，赵阳阳

(1.南京信息工程大学自动化学院，南京 210044； 2.江苏省大气环境与装备技术协同创新中心，南京 210044)

在数字网络控制环境中，由于实际信号传输的带宽限制，数据传输之前信号量化是必不可少的过程。量化控制分为静态量化控制[1]和动态量化控制[2-3]。静态量化器的量化参数固定，在实际应用中不能完全消除稳态误差和避免量化器饱和，所以针对静态量化器存在的问题，人们在此基础上加入动态参数提出了动态量化控制。目前主流的方法有在线检测技术[4]和离线计算技术[5]。它们的共同点是，当量化的信号发生测量饱和时，调整动态参数来增加量化范围，当量化的信号收敛时通过调整动态参数来降低量化误差的影响。

事件触发控制[6-9]可以确保系统稳定和性能的同时降低带宽要求，在满足某些预先设计的条件后进行采样，当采样误差超过一定阈值时确定采样时间并更新控制律。与动态量化控制的结合能更有效减少网络信号传送和节约网络资源。文献[7]中基于事件触发机制和量化控制策略，研究了离散时滞奇异马尔科夫跳变系统的控制器问题。在文献[8]中，系统的输出量化和控制输入量化由两个不同的动态量化器实现，并设计了一个动态输出反馈控制器，以确保统一的全局渐近稳定性和L2增益性能。对于非线性系统，文献[9]研究了在采样前量化和采样后量化情况下基于事件触发采样的非线性系统状态的动态量化控制。

滑模控制[10-11]是克服扰动和参数不确定性的有效工具。事件触发滑模控制[12-13]与量化反馈滑模控制[14-15]拥有良好的鲁棒性引起了相当大的关注。但是上述文献考虑的是理想情况下的量化过程，也就是编码器侧和解码器侧的量化器灵敏度参数一致。由于硬件缺陷，实践中量化器灵敏度参数不会完全保持一致。针对量化参数失配问题，文献[16]研究了时变比率模型和量化器灵敏度参数的不匹配关系，设计的滑模控制律可以保证系统的渐近稳定性。文献[17]研究了含有多个量化通道的线性系统的H2控制问题。在各通道量化参数不匹配的情形下，设计一种包含线性控制和非线性控制部分的复合控制方案，满足了H2性能要求并抵消量化误差。文献[18]针对信息物理系统，研究了执行器攻击和量化参数不匹配下的控制设计问题，设计的控制器可以消除量化误差，并实现对攻击的鲁棒补偿。文献[19]通过[K,KL]扇区的特点并设计基于开关逻辑的控制器来消除由于量化参数引起的不确定性。

在上述研究的基础上，现设计联合事件触发机制和动态量化策略的滑模控制方法。研究线性不确定系统中量化器饱和问题的同时，考虑编码器和解码器侧的量化器灵敏度参数的失配问题。编码器和解码器侧的量化器灵敏度参数更新均使用动态量化方法，提出一种量化器灵敏度变化率时变的离散在线调整策略。结合离散在线调整策略建立编码器和解码器侧量化参数失配的时变比例模型。将量化器的事件触发方案和提出的离散在线调整策略相结合，保证所设计的滑模控制器可以将系统状态驱动到期望的滑模面，对线性不确定系统具有良好的收敛性能，建立闭环系统的全局鲁棒镇定。

1 预备知识及问题描述

1.1 预备知识

Rn表示n维欧几里得空间，Z>0是正整数的集合，Z≥0包含Z>0和0。符号He(X)表示X+XT。sign(·)表示符号函数。‖x‖p是向量或矩阵的p范数。λmin(·)表示方阵的最小特征值。

1.2 问题描述

考虑一类不确定系统，表达式为

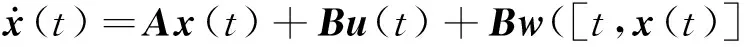
(1)

式(1)中：x(t)∈Rn为状态向量；u(t)∈Rm为控制输入，外部干扰w[t,x(t)]∈Rm；A∈Rn×n、B∈Rn×m分别为适当维数的系统矩阵和输入矩阵。

量化器被视为分段函数q:Rn→E，其中E是Rn的有限子集，结合事件触发机制和动态量化策略后，量化参数失配的量化器定义为

(2)

式(2)中：q(·)为取整函数；ti,i∈Z≥0表示事件触发的瞬间；x(ti)为事件触发机制后的状态信息；tk,k∈Z≥0为量化灵敏度参数的更新时刻；τc(tk)和τd(tk)分别为量化器qτ(tk)[x(ti)]在编码器侧和解码器侧的灵敏度参数。

事件触发机制定义为

ti+1=inf{t∈(ti,+∞):‖Ce(t)‖≥

α‖Cqτc(tk)[x(ti)]‖}

(3)

式(3)中：e(t)=x(ti)-x(t)为采样误差；α∈(0,β+1)是事件触发阈值参数；β为大于1的正参数；C∈Rm×n为切换向量。

量化器满足以下条件[15]：

‖x(ti)‖≤Mτc(tk)⟹‖eτ(tk)(ti)‖≤Δτc(tk)，

‖x(ti)‖>Mτc(tk)⟹‖qτc(tk)[x(ti)]‖>(M-Δ)τc(tk)，M为量化测量饱和参数，给出以下两个假设。

假设1系统(A,B)是可控的。

假设2干扰w[t,x(t)]满足‖w[t,x(t)]‖≤w1+w2‖x(t)‖2，w1和w2是已知的正实数。

用到引理1[20]:

对于任意的β>1，事件触发阈值参数α∈(0,1)，如果参数τc(tk)>0并满足

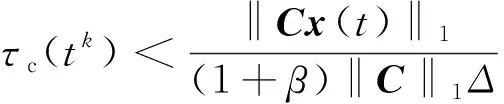
(4)

不等式(5)成立，即

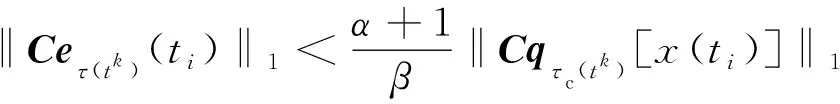
(5)

2 量化策略和控制器设计

2.1 滑模面设计

定义线性滑模面为

s(t)=Cx(t)=C1x1(t)+C2x2(t)=0

(6)

式(6)中：C∈Rm×n，C1∈Rm×(n-m)，C2=Im×m。

假设系统(1)的结构[21]为

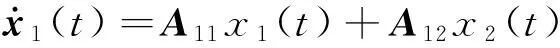
(7)

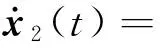
B2u(t)+B2w[t,x(t)]

(8)

式中：x1(t)∈R(n-m)，x2(t)∈Rm，A11∈R(n-m)×(n-m)，A12∈R(n-m)×m，A21∈Rm×(n-m)，A22∈Rm×m，B2∈Rm×m，将x2(t)=-C1x1(t)代入式(7)，有

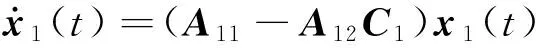
(9)

He[(A11-A12C1)TP]+Q<0

(10)

如果存在正定矩阵X=P-1∈R(n-m)×(n-m)，Z=Q-1∈R(n-m)×(n-m)和Y=C1X∈Rm×(n-m)满足线性矩阵不等式为

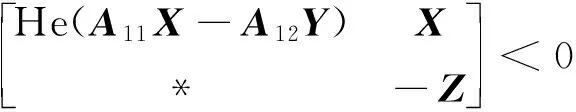
(11)

式(11)中：*表示矩阵中对于对角线的对称位置上的元素。

那么降阶系统[式(9)]是稳定的[20]。

2.2 量化参数失配的离散在线调整策略

量化失配无法给出具体的失配方式，所以动态量化中量化器灵敏度参数的变化率不能是一个固定值，而是一个保持在某一区间的随时间变化的不确定的值。结合动态量化构造了量化参数失配的量化器灵敏度参数τc(tk)和τd(tk)的离散在线调整方式，包括两个阶段：Zoom-out阶段(开环缩小阶段)和Zoom-in阶段(闭环放大阶段)，逻辑变量θ用于区分这两个阶段，形式如下。

(12)

通过在动态量化中加入时变量化器灵敏度参数变化率，建立编码器和解码器侧的量化参数的时变比例模型，量化器灵敏度参数τc(tk)和τd(tk)的离散更新如下。

(13)

(14)

2.3 控制器设计

滑模控制律的形式如下。

u(t)=u1(t)+u2(t)

(15)

u1(t)=-(CB)-1CAqτc(tk)[x(ti)]-

ksign{Cqτc(tk)[x(ti)]}

(16)

u2(t)=-φ(CB)-1sign{Cqτc(tk)[x(ti)]}×

(17)

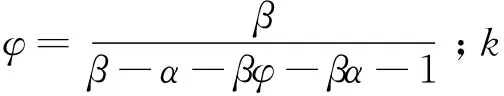
其中w*=w1+w2Δτc(tk)+w2(φ+1+α)‖qτc(tk)[x(ti)]‖∞。

2.3.1 定理1

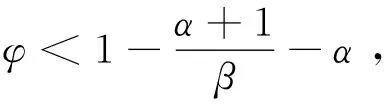
证明在Zoom-out阶段，控制输入u(t)为0，系统方程[式(1)]变为

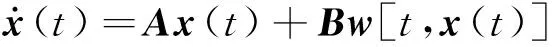
(18)

证明过程类似于文献[20]中的定理2的证明，可以得到

‖x(t)‖≤a1ea2t

(19)

根据动态量化机制，可以观察到在Zoom-out阶段，τc(tk)的更新速率快于系统的发散速率，存在时刻tk>t0，使得‖x(t)‖>Mτc(tk)和‖x(t)‖≤Mτc(tk+1)，此时系统状态被捕获，进入Zoom-in阶段，根据引理1[式(4)]，需要考虑两种情况。

将证明两种情况下状态轨迹会进入边界层区域。

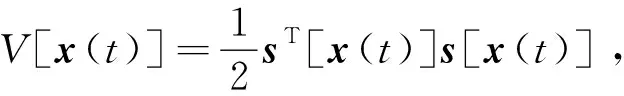
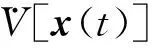
=[Cx(t)]T{CAx(t)+CBu(t)+

CBw[t,x(t)]}

(20)

因为eτ(tk)(ti)=r(tk)qτc(tk)[x(ti)]-x(ti)，e(t)=x(ti)-x(t)，有

Ce(t)}T{CA[r(tk)-1]qτc(tk)[x(ti)]+

CAqτc(tk)[x(ti)]-CAeτ(tk)(ti)-CAe(t)+

CBu(t)+CBw[t,x(t)]}

(21)

将式(16)代入式(21)可得

ksign{qτc(tk)[x(ti)]}-CAeτ(tk)(ti)-

[Ceτ(tk)(ti)+Ce(t)]T×

ksign{Cqτc(tk)[x(ti)]}-CAeτ(tk)(ti)-

(22)

整理后有

r(tk){Cqτc(tk)[x(ti)]}TCBu2(t)+

r(tk){Cqτc(tk)[x(ti)]}T{CA[r(tk)-1]×

qτc(tk)[x(ti)]-CAeτ(tk)(ti)-CAe(t)+

CBw(t,x(t)]}-

[Ceτ(tk)(ti)+Ce(t)]T×

ksign{Cqτc(tk)[x(ti)]}-CAeτ(tk)(ti)-

(23)

通过对r(tk){Cqτc(tk)[x(ti)]}TCBu2(t)进行放缩可得

[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

(1-φ){Cqτc(tk)[x(ti)]}TCBu2(t)+

r(tk){Cqτc(tk)[x(ti)]}T×

{CA[r(tk)-1]qτc(tk)[x(ti)]-

CAeτ(tk)(ti)-CAe(t)+CBw[t,x(t)]}-

[Ceτ(tk)(ti)+Ce(t)]T×

ksign{Cqτc(tk)[x(ti)]}-CAeτ(tk)(ti)-

(24)

因为‖XTY‖≤‖X‖1‖Y‖∞，不难得到

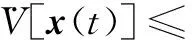
[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

(1-φ){Cqτc(tk)[x(ti)]}TCBu2(t)+

‖r(tk)‖1‖Cqτc(tk)[x(ti)]‖1×

{‖r(tk)-1‖∞‖CA‖∞×

‖qτc(tk)[x(ti)]‖∞+

‖CA‖∞‖eτ(tk)(ti)‖∞+‖CA‖∞×

‖e(t)‖∞+‖CB‖∞‖w[t,x(t)]‖∞}+

‖Ceτ(tk)(ti)+Ce(t)‖1×

{‖r(tk)-1‖∞‖CA‖∞‖qτc(tk)[x(ti)]‖∞+

k‖CA‖∞‖eτ(tk)(ti)‖∞+‖CA‖∞×

‖e(t)‖∞+‖CB‖∞‖u2(t)‖∞+

‖CB‖∞‖w[t,x(t)]‖∞}

(25)

注意到‖r(tk)-1‖≤φ，‖r(tk)‖≤φ+1，且‖eτ(tk)(ti)‖≤Δτc(tk)，结合引理1[式(4)]，可得

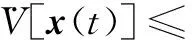
[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

‖CBu2(t)‖∞+

{Cqτc(tk)[x(ti)]}TCBu2(t)+

(φ+1)‖Cqτc(tk)[x(ti)]‖1×

[(φ+α)‖CAqτc(tk)[x(ti)]‖∞+

‖CA‖∞Δτc(tk)+

‖CB‖∞‖w[t,x(t)]‖∞]+

{(φ+α)‖CA‖∞‖qτc(tk)[x(ti)]‖∞+

k‖CA‖∞Δτc(tk)+‖CB‖∞×

‖w[t,x(t)]‖∞}

(26)

整理可得

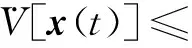
[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

{Cqτc(tk)[x(ti)]}TCBu2(t)+

CBu2(t)+‖Cqτc(tk)[x(ti)]‖1×

‖CA‖∞‖qτc(tk)[x(ti)]‖∞+

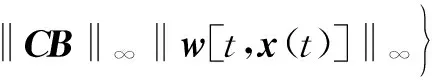
(27)

根据假设2，w*=w1+w2Δτc(tk)+(φ+1+α)w2‖qτc(tk)[x(ti)]‖∞，可得

‖w[t,x(t)]‖≤w1+w2‖x(t)‖≤

w1+w2‖r(tk)qτc(tk)[x(ti)]-eτ(tk)(ti)-

e(t)‖≤w1+w2[(φ+1+α)×

‖qτc(tk)[x(ti)]‖+Δτc(tk)]≤w*

(28)

将式(28)代入式(27)可得

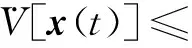
[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

‖CBu2(t)‖∞+

(φ+α)‖CA‖∞‖qτc(tk)[x(ti)]‖∞+

(29)

‖CB‖∞w*，可以得到

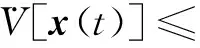
[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)+

‖CBu2(t)‖∞+

CBu2(t)+‖Cqτc(tk)[x(ti)]‖1×

(30)

另一方面，通过式(17)中u2(t)的设计,结合‖r(tk)-1‖≤φ，有

[r(tk)-1]{Cqτc(tk)[x(ti)]}TCBu2(t)+

φ{Cqτc(tk)[x(ti)]}TCBu2(t)≤0

(31)

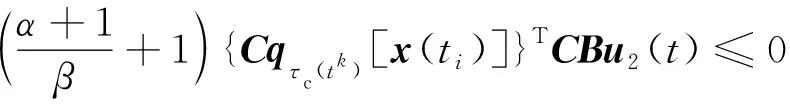
(32)

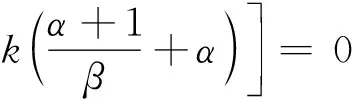
(33)

综合式(30)～式(33)，容易得到

(34)

对于∀a∈R,b∈R，不等式‖a+b‖1≤‖a‖1+‖b‖1成立，再结合引理1[式(4)]得到‖Cx(t)‖1≤‖Cr(tk)qτc(tk)[x(ti)]-

‖Cqτc(tk)[x(ti)]‖1

(35)

所以可得

(36)

两边同时乘以-kr(tk)，有

-kr(tk)‖Cqτc(tk)[x(ti)]‖1≤-kr(tk)×

(37)

因为‖a‖1≥‖a‖2，有‖Cx(t)‖1≥‖Cx(t)‖2，可以看到

(38)

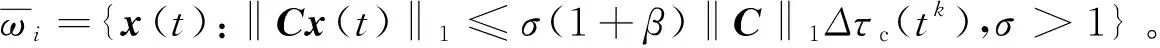
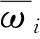
C1x1(t)+x2(t)=δσ(1+β)‖C‖1Δτc(tk)

(39)

因此可以得到

x2(t)=-C1x1(t)+δσ(1+β)‖C‖1Δτc(tk)

(40)

将式(40)代入式(7)得

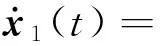
A12δσ(1+β)‖C‖1Δτc(tk)

(41)

[A12δσ(1+β)‖C‖1Δτc(tk)]TPx1(t)+

x1(t)PA12δσ(1+β)‖C‖1Δτc(tk)

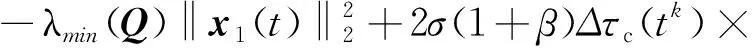
‖PA12‖2‖C‖1‖x1(t)‖2

(42)

所以

‖x1(t)‖2≤

(43)

因为‖x(t)‖2≤‖x1(t)‖2+‖x2(t)‖2，结合式(40)可得

‖x(t)‖2≤(1+‖C1‖2)×

σ(1+β)Δτ(tk)‖C‖1

(44)

‖x(t)‖2≤KΔτc(tk)

(45)

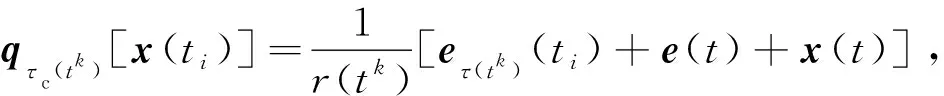
(46)

在式(46)两边同除以τc(tk)，得到

(47)

‖x(ti)‖2≤‖r(tk)‖2‖qτc(tk)[x(ti)]‖2+

‖eτ(tk)(ti)‖2≤

(48)

‖x(ti)‖2≤Mτc(tk+1)

(49)

事件触发控制中，如果相邻两次触发的时间间隔过小，也就是趋近于0时，控制器会无限次触发，也就是Zeno行为，需要证明事件触发间隔存在下限。

2.3.2 定理2

对于含有式(15)～式(17)控制器的不确定线性系统[式(1)]，事件触发机制满足式(3)，帧间时间Ti=ti+1-ti，i∈Z≥0在Zoom-out阶段和Zoom-in阶段分别满足

(50)

(51)

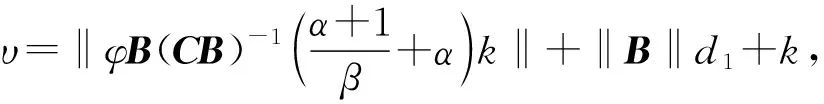
证明 Zoom-out阶段，根据假设2和e(ti)=0，考虑式(17)可得

‖x(t)‖+w1‖B‖≤

(‖A‖+w2‖B‖)‖e(t)‖+

(‖A‖+w2‖B‖)‖x(ti)‖+w1‖B‖

(52)

应用比较引理，可以得到

‖e(t)‖≤

[e(‖A‖+w2‖B‖)(ti+1-ti)-1]

(53)

根据事件触发机制可得

α‖qτc(tk)[x(ti)]‖≤

[e(‖A‖+w2‖B‖)(ti+1-ti)-1]

(54)

最后有

(55)

同理在Zoom-in阶段，不难看出

‖e(t)‖+(‖A‖+w2‖B‖)‖x(ti)‖+

‖B‖‖u(t)‖+‖B‖w1

(56)

最终可以得到

(57)

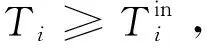
3 系统仿真

3.1 实例一

为了说明事件触发机制和量化器灵敏度参数失配的离散更新策略的有效性，考虑火箭整流罩声学结构模型[22]，系统矩阵、输入矩阵和外部干扰如下所示。

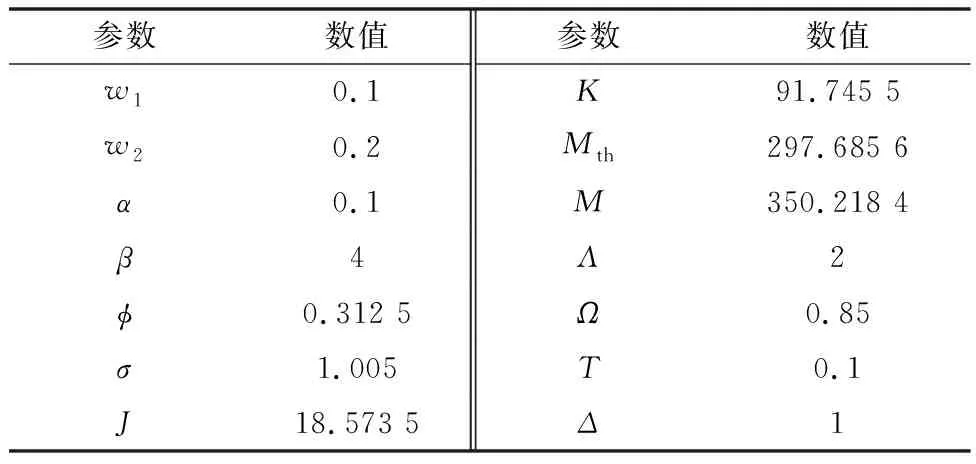
表1 仿真参数Table 1 Simulation parameters

表2 和 Table 2

表3 和Table 3

应用所提出的滑模控制律，结合提出的事件触发机制和量化参数失配的离散更新机制，仿真结果如图1～图8所示。

图1 系统状态响应曲线Fig.1 Response curves of system states

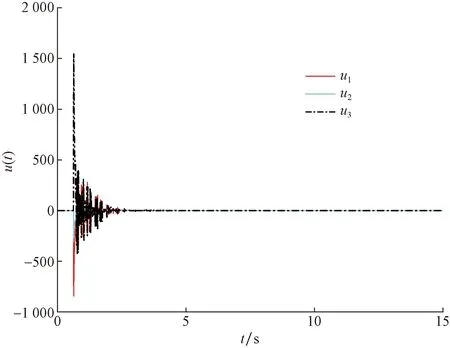
图2 系统控制输入响应曲线Fig.2 Response curves of system control inputs

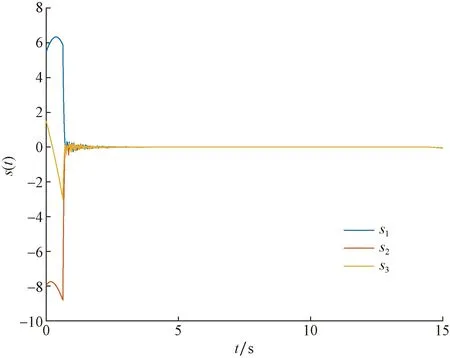
图3 滑动函数的响应曲线Fig.3 Response curves of the sliding function

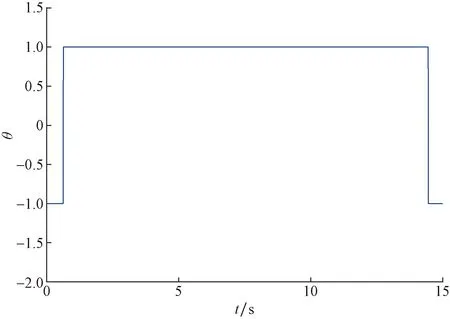
图4 逻辑变量θ Fig.4 Logical variableθ

图5 灵敏度参数τc(t)更新曲线Fig.5 Update curves of sensitivity parameter τc(t)

图6 帧间时间图Fig.6 Interframe time graph

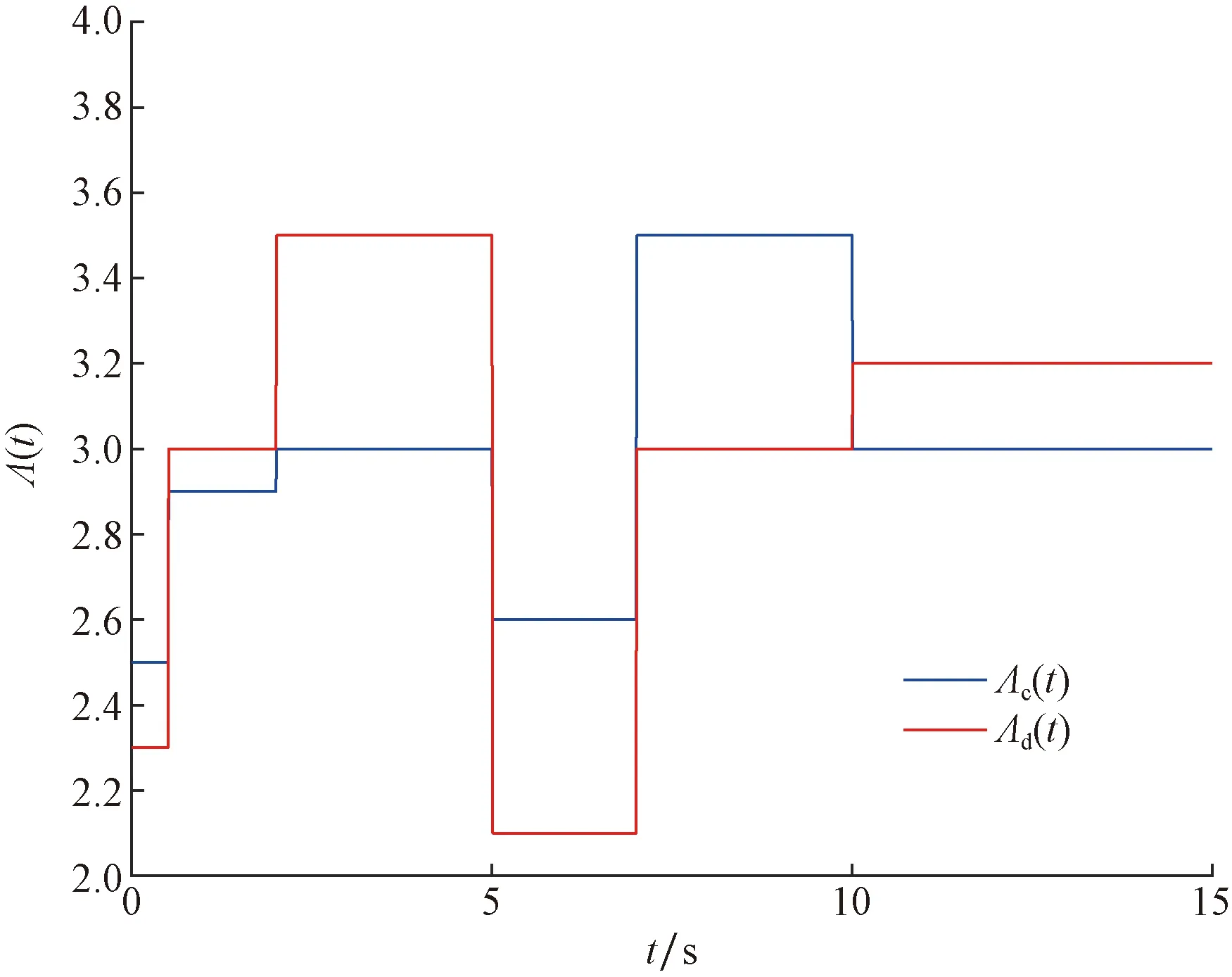
图7 和的变化图Fig.7 Variation diagram of

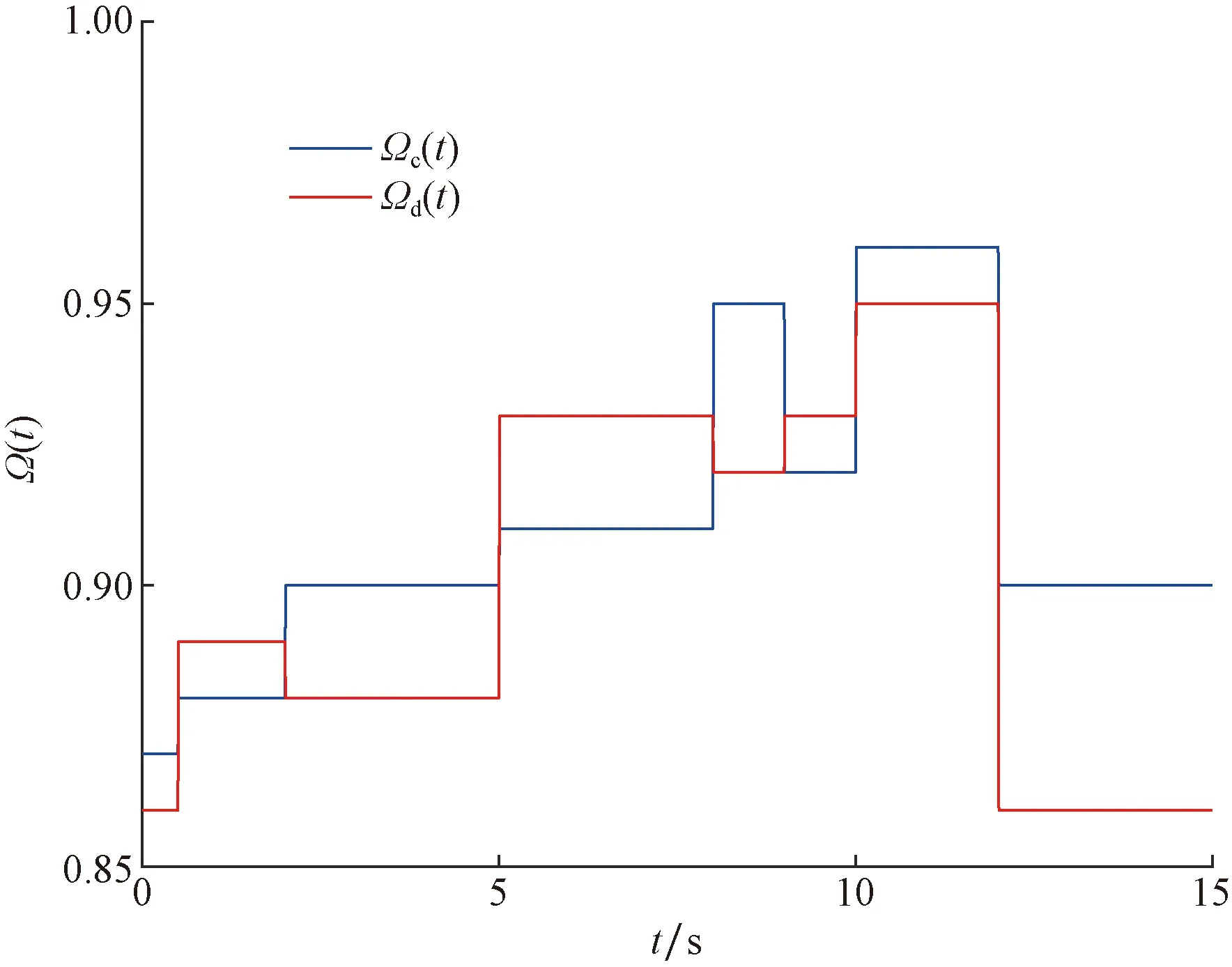
图8 和的变化图Fig.8 Variation diagram of

其中系统的响应曲线图如图1～图3所示，可以看出，设计的控制器在系统存在外部干扰和量化参数失配的情况下系统的状态、控制输入和滑模面均能收敛于原点并且趋近于稳定。

图4和图5中逻辑变量θ和灵敏度参数τc(t)都可以反映出系统都是从Zoom-out阶段转换到Zoom-in阶段，τc(t)在Zoom-out阶段持续变大，转换到Zoom-in阶段后持续变小。

图6给出系统的帧间时间，结果表明不存在Zeno行为。图7和图8显示在Zoom-out阶段和Zoom-in阶段τc(t)的变化率的不匹配情况，从表2和表3很容易看出，两个量化灵敏度参数在任何时候都不相等。

3.2 实例二

倒立摆是控制领域中重要的研究对象，为验证控制器的有效性，将文献[23]中的一级倒立摆作为实例二，倒立摆的表达式为

(58)

(59)

(60)

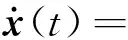
(61)

外部干扰w[t,x(t)]=0.01sin(2t)+0.02× cos(2t)x1(t)，初始状态x0=[0.09 0 0.06 0]T，选取Q=I3×3，C2=1，通过计算得到矩阵A和B的能控标准型，求得

量化器灵敏度参数τc(tk)和τd(tk)的变化率同表2和表3，实例二其余的参数选择如表3所示。

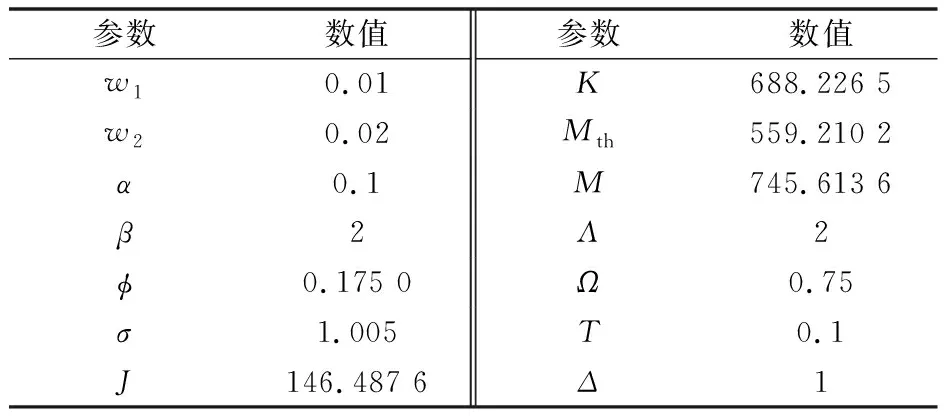
表3 仿真参数Table 3 Simulation parameters

仿真结果如图9～图14所示，系统状态、系统输入以及滑模函数的响应曲线如图9～图11所示，很容易看出，倒立摆系统具有良好的稳摆性能。

图9 系统状态响应曲线Fig.9 Response curves of system states

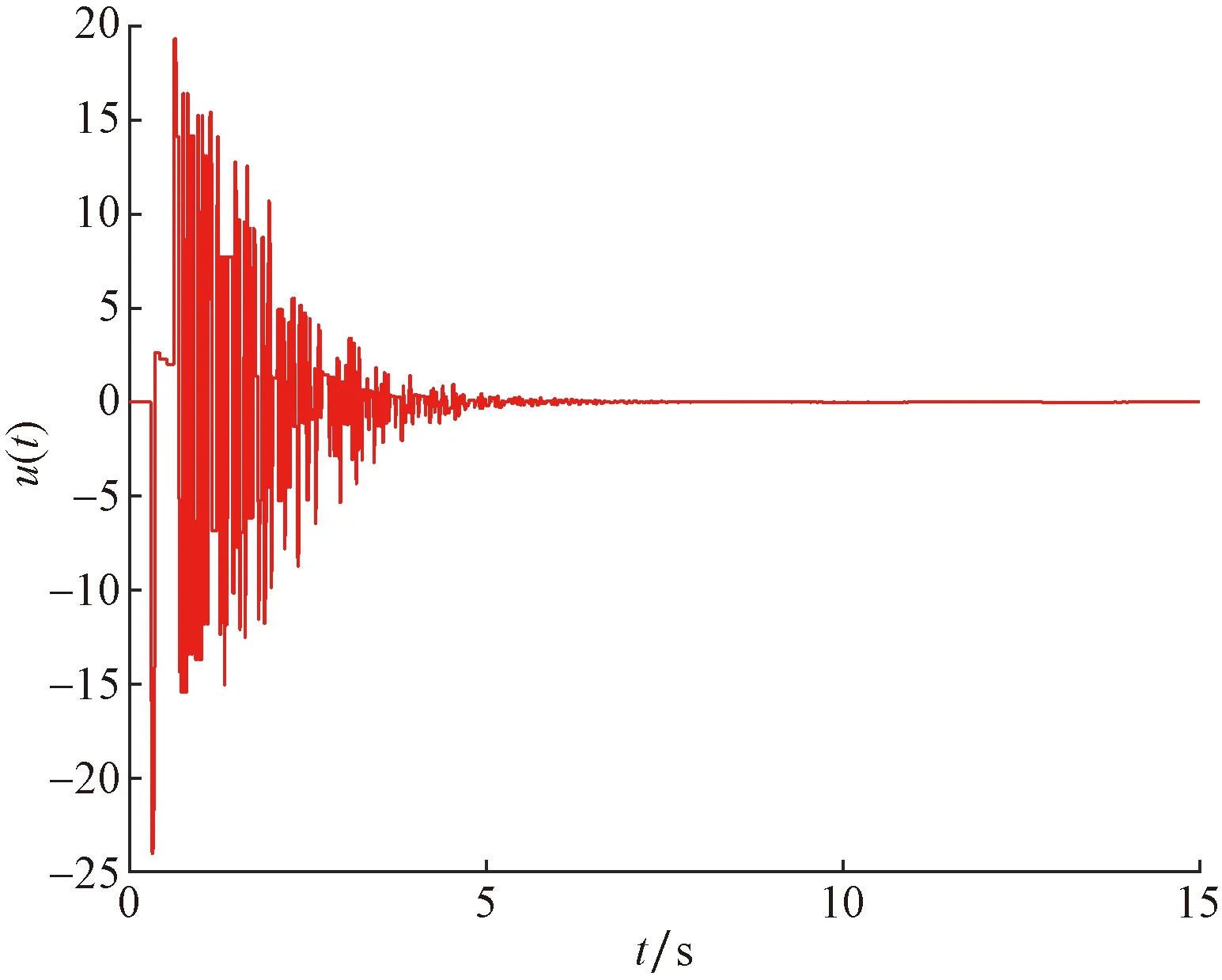
图10 系统控制输入响应曲线Fig.10 Response curves of system control input

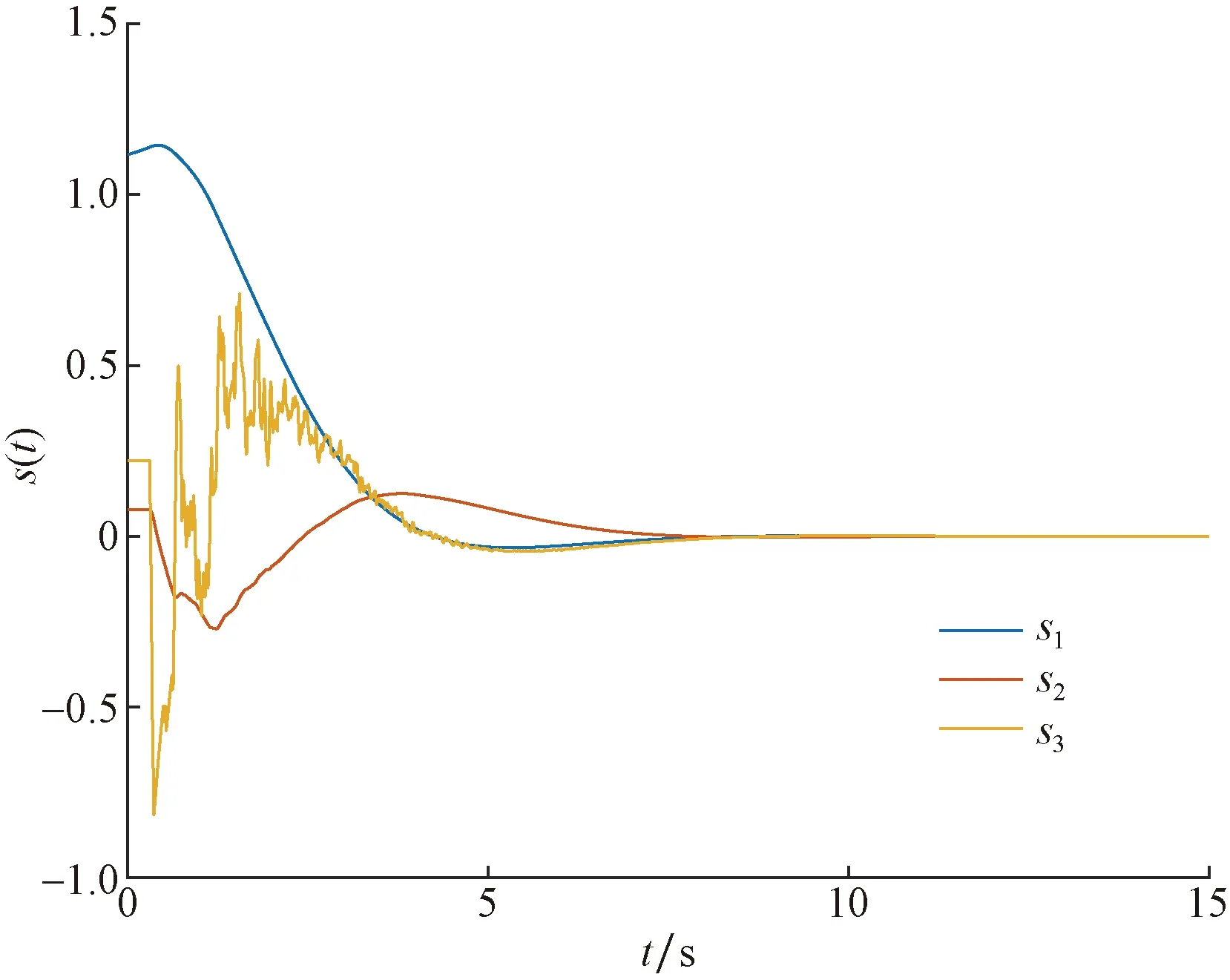
图11 滑动函数的响应曲线Fig.11 Response curves of the sliding function

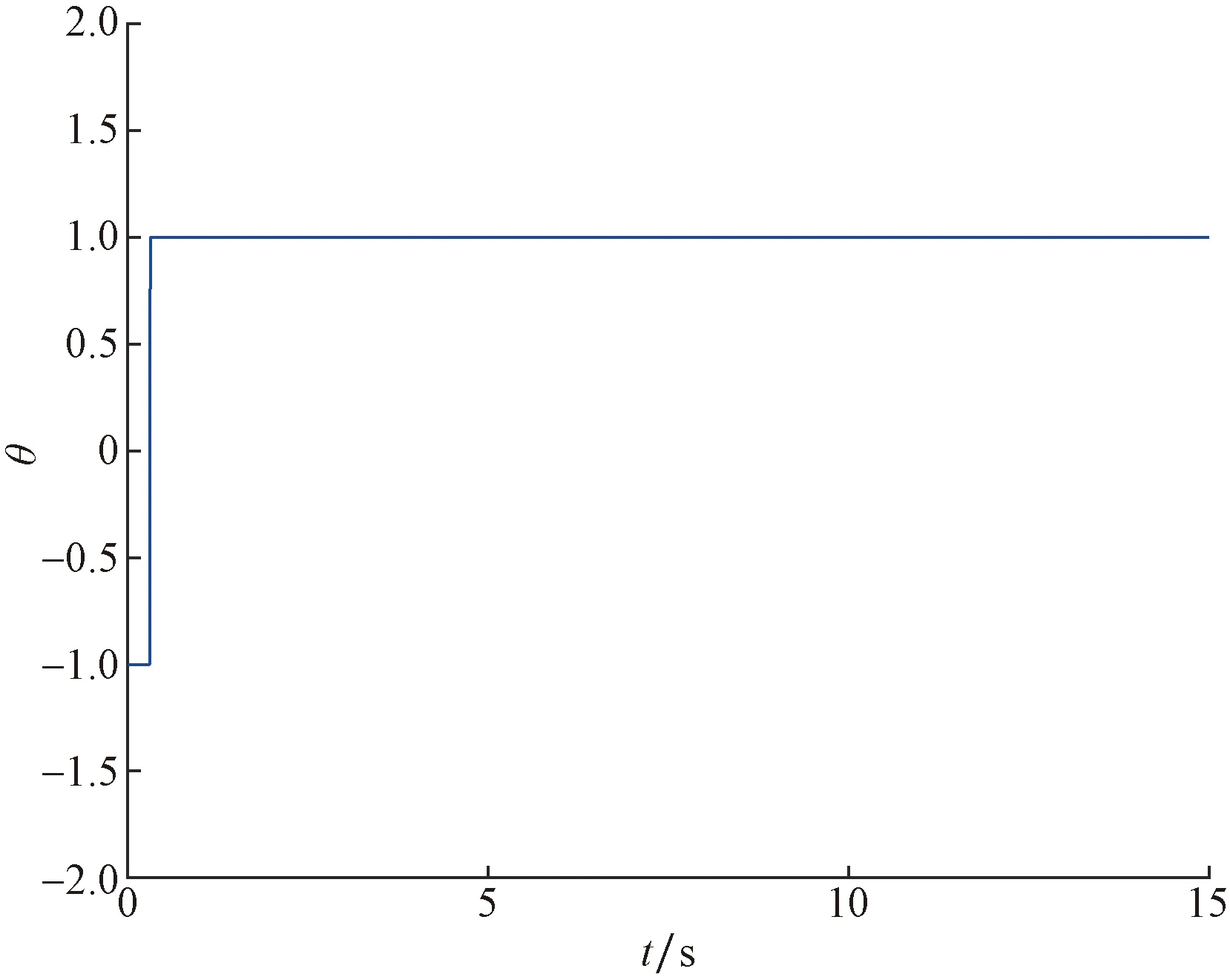
图12 逻辑变量θ Fig.12 Logical variableθ

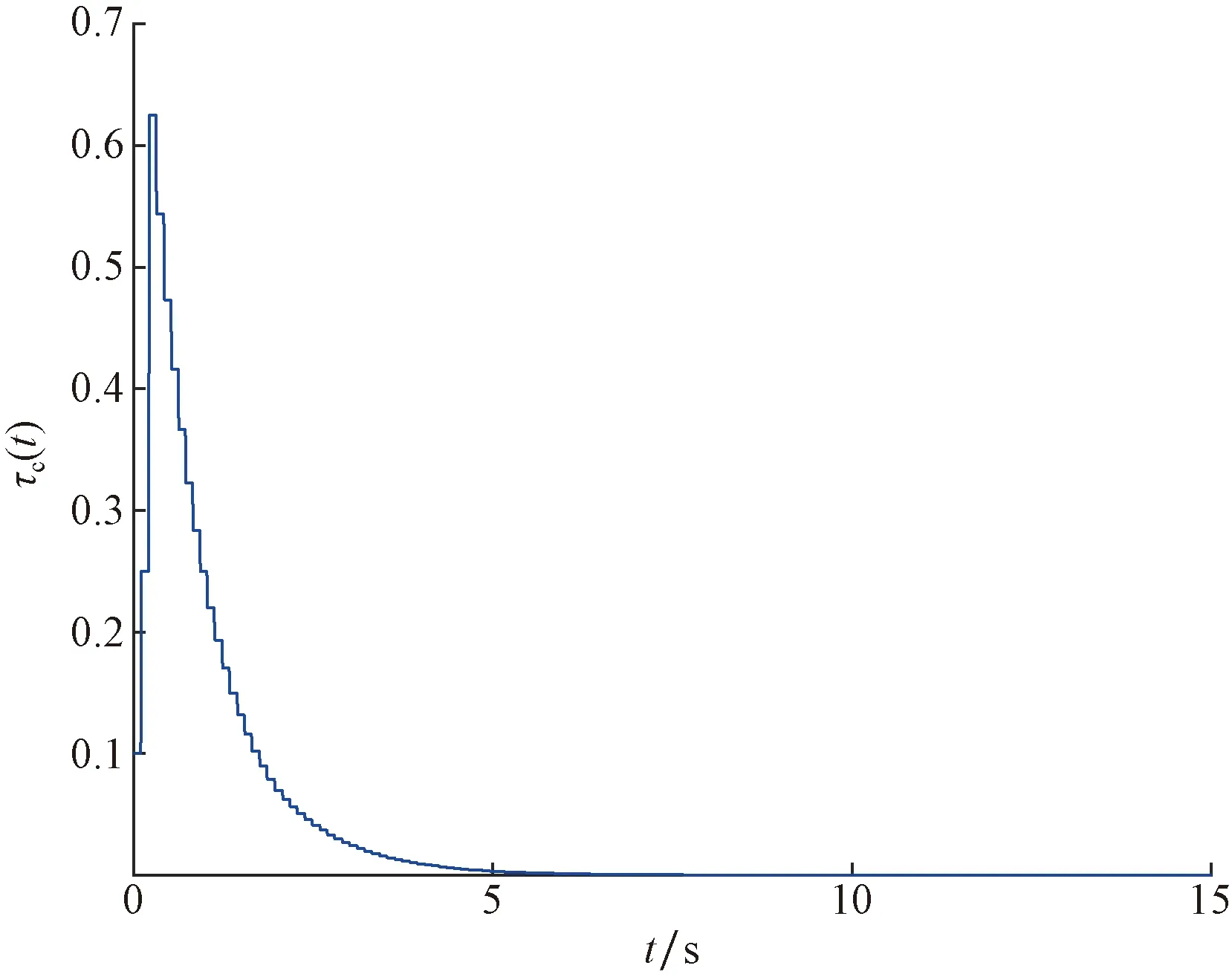
图13 灵敏度参数τc(t)更新曲线Fig.13 Update curves of sensitivity parameter τc(t)

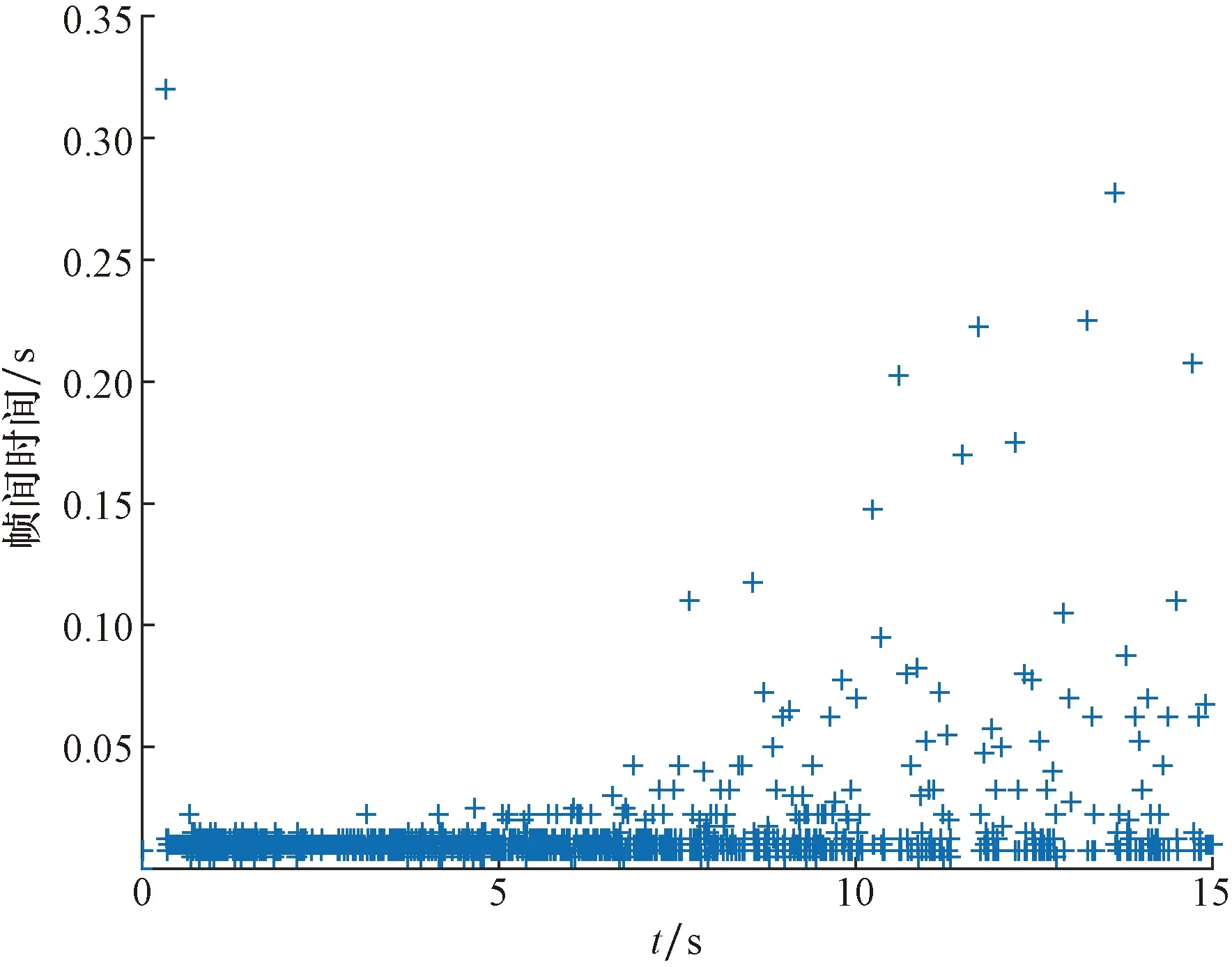
图14 帧间时间图Fig.14 Interframe time graph

图12和图13中逻辑变量θ和灵敏度参数τc(t)都可以反映出系统从Zoom-out阶段到Zoom-in阶段的转变，灵敏度参数按照离散调整策略在Zoom-out阶段持续变大，转换到Zoom-in阶段后持续变小。图14给出系统的帧间时间，结果表明不存在Zeno行为。

综上所述，可以看出，当存在外部干扰和量化参数失配时，设计的量化反馈滑模控制器可以保证倒立摆系统的稳定性。

4 结论

利用事件触发方法研究了具有量化参数失配和外部干扰的不确定线性系统的滑模控制器的鲁棒镇定问题。

(1)设计了一种含有时变量化器灵敏度变化率的离散在线调整策略，从而可以结合动态量化的方法来解决量化参数失配问题。

(2)提出了一种与量化器相关的事件触发机制，不会发生Zeno行为。

(3)结合事件触发机制和动态量化策略提出的滑模控制律可以有效地消除量化参数失配和外部干扰的影响，保证滑模运动的到达。为用事件触发方法和动态量化方法研究量化参数的失配下的状态量化和控制输入量化的滑模控制设计问题提供了新的思路。