热力耦合下CRC+AC复合式路面沥青层力学响应分析

李盛，孙煜，许路凯

(长沙理工大学 特殊环境道路工程湖南省重点实验室，湖南 长沙，410114)

连续配筋混凝土刚柔复合式沥青路面是在连续配筋混凝土(continuously reinforced concrete，CRC)上加铺沥青混凝土(asphalt concrete，AC)的一种复合式路面结构，是我国重载交通下一种重要的长寿路面结构形式[1]。这种路面结构具有承载能力强、行车舒适性高、耐久性较强以及养护维修方便等特点。国内外学者就许多单一因素对路面结构的影响进行了研究。温度是影响路面结构力学行为的重要因素。严作人[2]从定性与定量的角度分析了基层材料的热力学性质对路面结构温度场的影响规律，根据传热学原理推导出了层状路面体系的温度场解析解。LIU等[3]通过有限元模拟单轴压缩试验研究了温度对沥青混合料力学性能的影响，发现随着温度升高，沥青与集料界面处的最大压缩主应力减小。目前，人们对CRC+AC 刚柔复合式路面结构温度场进行了大量研究。韩文扬等[4]对CRC+AC复合式路面结构的温度场和温度梯度进行了实测，分析了温度场影响因素的滞后性与累积规律。顾兴宇等[5]运用传热学原理，利用ABAQUS 有限元程序，对CRC+AC 复合式路面的瞬态温度场进行了有限元分析，得到的温度场规律与韩文扬等[4]通过实测得到的规律非常一致。王骁帆等[6]通过有限元分析了温度场对连续配筋水泥混凝土路面纵向配筋率的影响，提出了考虑温度场作用的CRCP纵向配筋率设计方法。车辆荷载是影响路面结构的另一重要因素，国内外学者就力学响应的研究方法、有限元方法荷载模拟方式、力学响应以及对CRC+AC 刚柔复合式路面的设计优化进行了研究。OLSSON[7]使用理论解析法和有限元法计算了路面在移动荷载作用下的力学响应，发现有限元法更适合计算路面力学响应问题。HUANG等[8]使用ABAQUS有限元软件计算路面结构在移动荷载下的动力响应，发现计算结果与实际测量结果较吻合，表明有限元方法的准确性。对于车辆轴载与路面接触面问题，胡小弟等[9]建立了三维有限元模型，分析了不同的沥青路面结构在不同车辆荷载、不同分布状态的作用力作用下的力学响应，发现非均匀分布荷载对沥青路面的力学响应远大于均匀分布荷载对沥青路面的力学响应。胡小弟等[10-11]建立了子午线轮胎滚动分析的三维有限元模型，得到路面对轮胎的方向作用力与转速的关系，认为轮胎接地区域与接触面积、轮胎胎面花纹类型和轮胎与路面接触 应力有关。在车辆动荷载模拟问题上，BORROS 等[12]得到了层状黏弹性半空间体在匀速移动点荷载和线荷载作用条件下的动态响应解。邓学钧等[13]通过结合有限元和无限元，推导出半正弦荷载作用下的动态响应理论解。在路面结构力学响应问题上，李江等[14]通过建立路面结构应力随速度变化的路面模型，得出应力随着行车速度减小而呈线性增加，刹车频繁的区域水平应力会更大。董泽蛟等[15]采用实测车辆轴载建立了三向非均布移动荷载有限元模型，输入实测沥青混合料的动态模量，发现荷载移动作用下路面结构应力呈波动性变化，剪应力主要出现在路面的中面层。邓凤祥等[16]运用有限元法，对CRC 层带缝状态下的沥青层层底最大剪应力进行了计算与分析。国内外研究者对车辆荷载对路面结构影响的研究很多，但这些研究没有考虑温度对路面结构的影响。李盛等[17]采用有限元法分析了CRC+AC 复合式路面结构温度和应力分布，发现在一定范围内增加沥青层厚度可有效降低路面开裂风险。李盛等[18]进一步计算了CRC+AC 复合式路面在温度和荷载综合作用下的Top-Down 裂缝扩展，发现拉应力和剪应力是影响纵向裂缝发展的主要因素。路面结构在实际工作中受温度和车辆荷载作用的综合影响，两者的影响不是简单相加，国内外很多学者为此对路面结构热力耦合进行了研究。关于半刚性基层路面结构，ASSOGBA等[19]通过有限元分析了路面在非线性温度梯度和移动荷载综合影响下的力学响应，实验结果证明其建立的模型能准确预测温度随路面深度的非线性特征分布以及路面对非线性温度梯度和交通荷载的综合影响的响应。SI 等[20]通过伯格模型建立沥青粘弹性本构方程，推导出沥青路面热力-水力非线性控制方程，利用ABAQUS软件建立沥青路面有限元模型，分析了热力-水力耦合下沥青路面的力学响应，发现与单一应力相比，不同结构层的应力有所增加。对于普通水泥混凝土路面，郭超等[21]基于随机有限元法，对水泥路面在温度应力与随机车辆荷载耦合作用下最大Mises应力进行统计回归分析，确定了水泥路面应力的概率分布模型与可靠度指标。张磊等[22]运用有限元分析软件建立了CRC+AC 刚柔复合式路面热力耦合模型，对夏季时热力耦合下路面的损伤进行了分析，发现沥青层可以有效减小CRC 层的损伤。

综上可知，虽然有很多国内外学者对路面结构温度场、力学响应进行了研究，但针对路面结构热力耦合下力学响应的研究较少且大多针对半刚性基层。刚柔复合式路面沥青层的力学响应与普通半刚性基层沥青路面的力学响应并不相同，因此，有必要单独对CRC+AC 复合式路面进行研究，以揭示CRC+AC 刚柔复合式路面沥青层的力学行为和开裂机理。为此，本文作者以传热学为基础，运用Fortran 语言编制子程序，扩展大型有限元软件ABAQUS 主程序的功能，定义随时间变化的外界温度并进行稳态和瞬态热传导分析，模拟不同地区连续变温条件下CRC+AC 复合式路面结构的温度场，建立CRC+AC 复合式路面热力耦合模型，并采用“足尺路面试验环道”实测结果验证模型的可靠性，分析沥青层厚度、车辆轴载、行车速度、CRC层微裂缝(纹)宽度对沥青层力学响应的影响。

1 有限元模型建立及验证

1.1 温度场建立与验证

将路面结构简化成层状弹性体系，对各结构层进行以下假设：

1)各结构层为各向同性、完全连续、均质的线弹性体，其应力应变之间的关系符合广义胡克定律；

2)各结构层的层间接触状态为完全连续，有足够的摩擦力，不发生滑动，热传导连续；

3)路基在水平和深度方向无限延伸，面层、基层、垫层只在水平方向无限延伸；

4)路面在垂直均布荷载作用下，无限远和无限深处应力和位移均为0；

5)温度变化不随水平坐标的变化而变化，只与厚度有关。

利用ABAQUS 有限元计算程序计算路面结构在各种工况下的应力应变响应时，无法将模型尺寸设置成无限大，只能尽可能设定较大的模型尺寸以保证计算结果的精确性，但是较大的模型尺寸会大大增加计算量，为此，模型沿行车方向取7.5 m，沿垂直行车方向取7.5 m(双车道)，沿深度方向取10.0 m，建立的CRC+AC 复合式路面三维有限元计算模型的模型尺寸如图1所示，其中，Ei(i=1，2，3，4)为第i层结构层弹性模量，μi(i=1，2，3，4)为第i层结构层泊松比。结合现行规范[23]和实体工程调查结果，选取连续配筋混凝土板横向裂缝间距为1.5 m，裂缝宽度为0.5 mm。

图1 计算模型示意图Fig.1 Schematic diagram of calculation model

各结构层计算参数如表1所示，各结构层温度计算参数如表2所示。CRC 板纵向钢筋采用直径为16 mm螺纹钢筋，配筋率为0.6%；横向钢筋采用直径为12 mm 螺纹钢筋，配筋率为0.1%。钢筋设置在板中位置，采用裂缝虚拟填料的方法模拟传荷作用。

表1 模型计算参数Table 1 Model calculation parameters

采用“足尺路面试验环道”刚性基层沥青路面结构中不同深度预埋的温度传感器采集的数据验证CRC+AC 复合式路面温度场仿真模型的可靠性。选用“足尺路面试验环道”STR5 段刚性基层沥青路面对CRC+AC复合式路面温度场进行验证，路面结构如表3所示。计算时，有限元模型宽取7.5 m(双车道)，沿行车方向取7.5 m，沿深度方向取10.0 m。混凝土采用DC3D4 四结点线性传热四面体实体单元。路面结构层温度场计算参数如表2与表4所示。

表2 温度场计算参数Table 2 Temperature field calculation parameters

表3 足尺环道STR5段刚性基层沥青路面结构组成Table 3 Structural composition of rigid base asphalt pavement in STR5 section of full-scale ring road

表4 路面材料热物性参数Table 4 Thermophysical parameters of pavement materials

根据传热学理论，运用Fortran 语言编制子程序，定义随时间变化的外界温度，并对连续变温条件下CRC+AC 复合式路面结构的稳态和瞬态热传导进行模拟与分析。CRC+AC 复合式路面结构某时刻的温度场云图如图2所示。

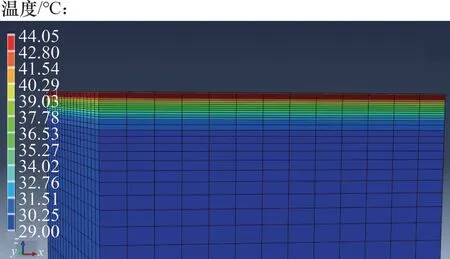
图2 CRC+AC复合式路面结构温度场云图Fig.2 CRC+AC composite pavement structure temperature field cloud map

将计算温度与足尺环道沥青混凝土路面STR5段实测温度进行比较，结果如图3所示。

图3 不同深度处温度的计算值与实测值比较Fig.3 Comparison of calculated and measured temperature at different depths

从图3可知：温度模拟计算值与实测值的变化趋势一致，最大误差为4.7%。误差的产生可能与ABAQUS 有限元软件的计算逻辑、模型材料参数以及气象参数的设置有关，路面所处的环境并不是一成不变的，如受云量、风速、湿度和行车荷载等因速变化的影响。该误差在合理范围内，因此，可认为所建立的温度场计算模型是合理、可靠的，可用于分析路面结构热力耦合下的力学响应。

1.2 热力耦合模型建立及验证

采用顺序耦合分析方法，使用ABAQUS 有限元软件建立CRC+AC 复合式路面温度和三向非均布荷载耦合分析模型。先进行稳态和瞬态传热分析得到不同时刻不同位置的单元节点温度，然后对温度和三向非均布荷载耦合进行分析。

1.2.1 模型计算参数

模型尺寸与温度场模型尺寸相同，模型计算参数如表1所示，计算模型示意图如图1所示。采用八节点实体单元进行建模，边界条件为行车方向前后两侧限制沿X轴方向位移、绕X轴转动和绕Y轴转动，左右两侧限制沿Z轴方向位移、绕X轴转动和绕Y轴转动，模型底面限制任意方向的位移和转动。

1.2.2 三向非均布荷载

我国现行沥青路面设计规范中采用的是圆形均布荷载，但在实际中，轮胎与地面接触较复杂。为了更好地模拟轮胎与地面的实际受力情况，减小误差，考虑到货车和大型客车使用的大多为纵向花纹的子午线轮胎，因此，轮胎模型选定子午线轮胎，双轮中心间距为30 cm，轮胎与路面的接触模型如图4[19]所示，其中，q1，q2和q3表示横向水平力，f1，f2和f3表示纵向水平力，P1，P2和P3表示接地花纹的压力。

将车辆荷载简化为固定位置的冲击荷载，模拟分析行车荷载效应下沥青路面结构的动力响应问题。呈半正弦函数变化的荷载强度模型为

式中：P( )t为半正弦波荷载，MPa；Pmax为荷载强度峰值，MPa；T为动荷载作用周期，s；v为车辆行驶速度，m/s；R为轮胎与地面的接地当量圆半径，取10.65 cm。

行车荷载采用标准双轮轴载100 kN，子午线轮胎的纵向花纹对地面的压力如表5所示。根据国内学者研究结果[15]，当车辆正常行驶时，横向水平力系数取0.18，方向垂直于行车方向，如图4所示；纵向水平力系数取0.2，方向与行车方向相反。不同轴载下轮胎接地压力取值如表5所示。

图4 轮胎接地简化模型Fig.4 Simplified tire contact model

表5 轮胎接地压力取值Table 5 Tire ground pressure value MPa

1.2.3 模型可靠性验证

使用G60湘潭至邵阳高速公路CRC+AC复合式路面结构实体工程在8:00由FWD采集的弯沉值和测弯沉当天24 h 的实测气温对模型可靠性进行验证，其路面结构为4 cm 厚改性沥青SMA-13+6 cm厚改性沥青AC-20C+18 cm 厚连续配筋混凝土+3 cm 厚AC-10 调平隔离层+旧混凝土路面。首先使用ABAQUS 建立的温度场子程序，根据表6 中实测24 h 温度计算路面结构模型8:00 时路面结构的温度场，再将温度场导入热力耦合模型计算路面弯沉值。将FWD对路面施加的荷载简化成峰值为0.714 MPa、荷载作用半径为15 cm、作用时间为30 ms 的半正弦函数圆形均布荷载(见表7)，弯沉实测值与计算值对比见图5。

表6 日周期24 h的实测气温Table 6 Actual temperatures in 24 h ℃

表7 FWD荷载半周期加载变化量Table 7 Load change in half cycle of FWD

图5 有限元计算弯沉和FWD实测弯沉对比图Fig.5 Comparison of finite element calculated deflection and measured deflection by FWD

由图5 可见：ABAQUS 模型计算值曲线与FWD 实测弯沉值曲线非常接近，误差较小，最大误差为6.3%。因此，可认为建立的热力耦合模型反映合实际情况，可以用于CRC+AC 复合式路面的力学影响因素分析。

1.3 温度场的模拟与分析

1.3.1 温度场模拟

利用ABAQUS 有限元软件模拟CRC+AC 复合式路面结构的温度场，分别使用子程序FILM和子程序DFLUX 体现“气温及对流热交换”过程和“太阳辐射”过程，输入1 d 中24 h 的大气温度并进行稳态和瞬态热传导分析，模拟连续变温条件下CRC+AC 复合式路面结构的温度场。在低温条件下，路面结构收缩受拉，容易开裂，因此，使用表8中某地区低温季节数据模拟温度场。该地区日太阳辐射总量为9.14 MJ/m2，日平均风速为2.9 m/s，日照时间为9.5 h。

表8 某地区低温季节1 d中24 h的实测气温Table 8 Temperature of 24 h on a certain day in the low temperature season in a certain area ℃

路面材料内部会有热量的吸收和散发，由于吸热和散热不同步，会有热量在路面内部积累，故在进行有限元模拟时要经过多个温度变化周期计算。施加4个温度周期后，路面结构层的温度变化基本稳定，所以，采用路面结构施加4个温度周期以后的温度场。在路面结构不同深度，5个周期温度变化曲线如图6所示。

图6 路面结构不同深度5个周期温度变化曲线Fig.6 5 cycles of temperature change curves at different depths of pavement structure

1.3.2 温度场分析

使用表8中温度施加4个温度周期后，路面结构层的温度变化基本稳定。路面不同深度24 h 的温度变化如图7和图8所示。

由图7和图8可见：路面温度从0:00开始呈现先降低再升高然后再降低的趋势，随气温的变化同步变化；沥青面层受外界气温影响最大，且幅度最大；在6:00 左右时深度0.04 m 和0.08 m 处的温度最低；当深度超过0.8 m时，温度变化幅度基本平稳，路面结构层温度均在-6 ℃以上。因此，可认为该地区冬季6:00 时路面最容易产生裂缝，后续计算分析均采用6:00左右的温度场。

图7 路面结构温度场Fig.7 Temperature field of pavement structure

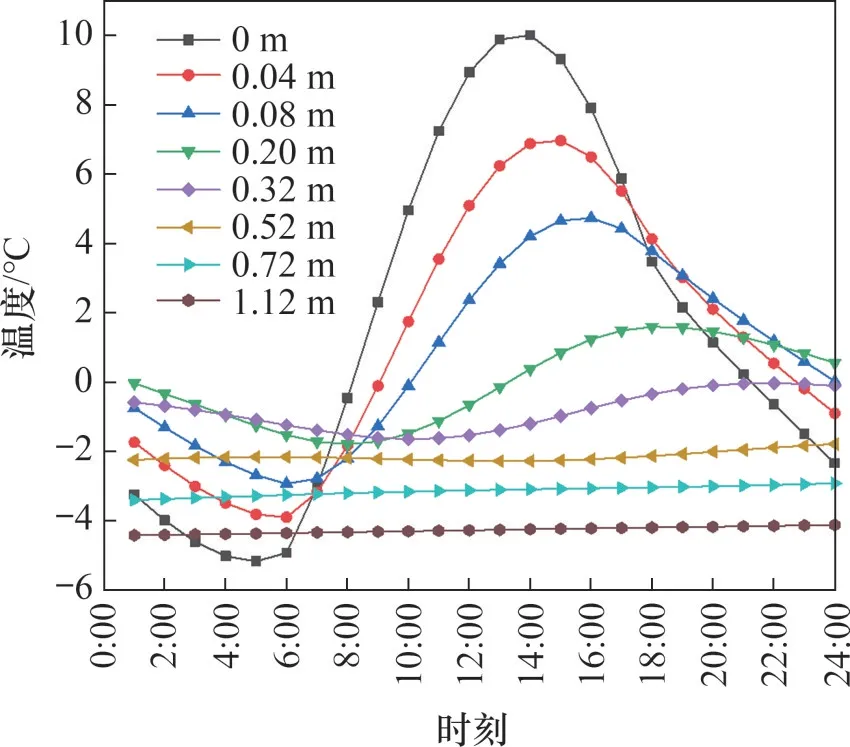
图8 路面不同深度24 h温度变化Fig.8 Temperature change in 24 h at different depths of road surface

2 CRC+AC复合式路面沥青层力学响应影响因素分析

影响CRC＋AC复合式路面力学响应的影响因素较多，除沥青混合料材料和路面结构等内在因素外，还有交通条件以及气候条件等外在因素。超载会导致轮胎对路面的接地应力增加，对路面产生较大的负荷，低速行驶会使荷载作用与路面的时间增加对路面产生较大的应力，高速行驶会对路面产生较大的冲击，且容易发生交通事故。在横向裂缝后施加式(1)中的半正弦波三向非均布荷载，分别研究沥青层厚度、车辆轴载、行车速度以及CRC 层裂缝(纹)宽度对沥青层力学响应的影响。

2.1 沥青层厚度对沥青层力学响应的影响

为研究沥青层厚度对沥青层力学性能的影响，保持CRC+AC复合式路面各结构层相关参数不变，引入冬季某天6:00 左右的温度场，仅改变沥青层的厚度，分别取沥青层厚度为6，8，10，12 和14 cm，分析沥青层厚度对CRC+AC复合式路面在温度和三向非均布动荷载耦合作用下沥青层力学响应的影响规律。

从图9 可以看出：随着沥青层的厚度从6 cm增加到14 cm，沥青层表面的横向应力降低4.90%，沥青层表面的纵向应力降低6.00%，表面剪应力几乎没有减小；沥青层底面横向应力降低88.90%，沥青层底面纵向应力降低88.70%，沥青层底面的剪应力降低56.70%；当沥青层较薄即沥青层厚为6 cm 时，沥青层表面和底面的拉应力均较大，沥青表面的剪应力小于底面的剪应力；随着沥青层厚度增加，表面拉应力与剪应力略微降低，而层底拉应力与剪应力降低幅度较大，且拉应力与剪应力的减小率越来越小。

图9 沥青层厚对沥青层应力的影响Fig.9 Influence of asphalt layer thickness on asphalt layer stress

分析结果表明沥青层厚度变的化对沥青层底部应力影响较大，合理控制沥青层的厚度可以减小沥青层推移与反射裂缝等病害。

2.2 车辆轴载对沥青层力学响应的影响

为研究超载对沥青层力学响应的影响，保持CRC+AC 复合式路面各结构层相关参数不变，其他参数不变，对路面施加不同轴载的接地压力，引入冬季某天6:00 左右的温度场，分别取轴载为100，120，140和160 kN，分析轴载对沥青层力学响应的影响。

不同轴载下CRC＋AC复合式路面沥青面层的应力变化如图10所示。从图10可见：轴载对沥青层的应力有很大影响；当车辆轴载从100 kN 增加至160 kN 时，沥青层表面的横向应力和纵向应力均减小2.00%左右，剪应力增加24.10%；沥青层底的横向应力减小56.6%，沥青层底的纵向应力减小62.10%，沥青层底的剪应力增加85.50%。沥青层表面和底面的拉应力均随车辆轴载增加而降低，这是因为低温时温度应力为正，而荷载产生的应力为负，在温度和荷载耦合作用下，沥青层拉应力会随荷载增大而降低，沥青底面的拉应力降低幅度更大，且层底拉应力减小率随着轴载增加呈降低趋势。沥青层表面和底面的剪应力均随着车辆轴载增加而增加，但沥青层底的增加幅度更大，且层底和表面剪应力的增长率随着轴载增加呈降低趋势。

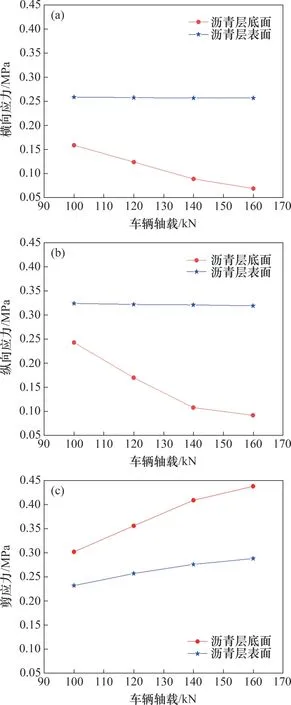
图10 车辆轴载对沥青层应力的影响Fig.10 Influence of vehicle axle load on asphalt layer stress

从分析结果可以看出，超载会使CRC+AC 复合式路面过早地出现裂缝、车辙等病害，影响道路的使用性能和使用寿命，因此，应严格控制车辆超载，防止路面长期处于超负荷工作状态。

2.3 行车速度对沥青层力学响应的影响

为分析不同行驶速度对沥青层的影响，保持其他参数不变，引入冬季某天6:00左右的温度场，取车辆轴载为100 kN，行车速度分别为60，80，100和120 km/h，分析车速对沥青层力学响应的影响规律。

在不同行车速度下，CRC＋AC 复合式路面沥青面层的应力变化如图11所示。从图11 可见：当行车速度从60 km/h 增加到120 km/h 时的过程中，沥青层表面的横向应力和纵向应力几乎没有变化，沥青层底的横向应力增加13.80%，沥青层底的纵向应力增加18.50%；行车速度变化对沥青层表面和底面剪应力的影响接近，沥青层表面剪应力减小12.00%，沥青层底的剪应力减小11.50%；沥青层底面的拉应力随行车速度的增加而增加，这是因为冬季低温时温度应力为正，荷载产生的应力为负，高速行驶会减小荷载作用在路面的时间，使路面结构内应力传播不充分，沥青层的耦合拉应力会随行车速度的增加而增加，速度越小，车辆作用前后的拉应力变化幅度越大。

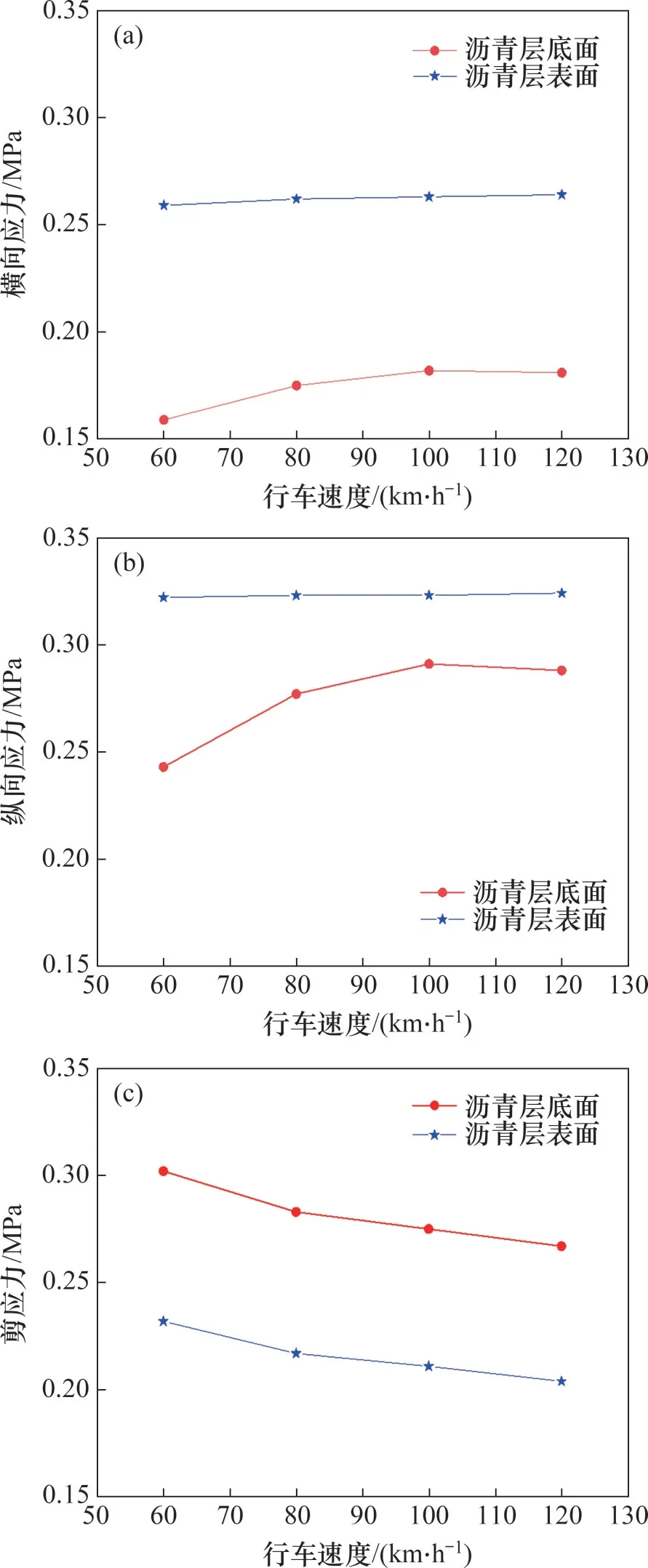
图11 行车速度对沥青层应力的影响Fig.11 Influence of driving speed on stress of asphalt layer

从上述分析结果可以看出，低速行驶更容易对路面产生破坏，影响道路的使用性能和使用寿命，但速度过高会使车辆对路面的冲击加大，加速路面结构的破坏。

2.4 CRC 层微裂缝(纹)宽度对沥青层力学性能的影响

为分析不同CRC层微裂缝(纹)宽度对沥青层的影响，引入冬季某天6:00 左右的温度场，保持其他参数不变，CRC 层微裂缝(纹)分别取0.5，0.7，0.9，1.1 和1.3 mm，研究不同CRC 层裂缝宽度下沥青层的力学响应，结果如图12所示。

由图12 可知：随着CRC 层微裂缝宽度从0.5 mm 增加到1.3 mm，沥青面层表面的应力几乎没有影响，沥青层表面剪应力减小3.00%，沥青层底横向应力增加40.20%，沥青层底纵向应力增加60.10%，沥青层底剪应力增加20.50%。沥青层底面的拉应力随CRC 层微裂缝(纹)宽度增加而增加，且层底纵向拉应力的增加率比横向拉应力更大，这是因为设置的CRC层微裂缝(纹)是横向的。CRC层微裂缝(纹)对应的沥青层底部的剪应力也随CRC层微裂缝(纹)宽度增加而增加。

图12 CRC层微裂缝(纹)宽度对沥青层应力的影响Fig.12 Influence of width of micro-cracks in CRC layer on stress of asphalt layer

从上述分析结果可以看出，CRC层微裂缝(纹)宽度变化对沥青层底部的拉应力和剪应力影响很大，在温度与荷载耦合作用下，CRC层微裂缝(纹)越宽对应的沥青层底部混合料容易被拉裂，后期会扩展形成反射裂缝；剪应力增加会加速沥青层底部反射裂缝的扩展，最终形成贯穿沥青层的横向裂缝。

3 CRC+AC复合式路面沥青层力学响应影响因素敏感性分析

3.1 正交试验方案设计

根据正交表的选用原则，通过4因素4水平正交试验(L16(44))方案对敏感性进行分析，对影响因素(沥青层厚度、轴载、车速、CRC微裂缝宽度)均赋予4个取值，分析上述因素对沥青层表面和底面应力的影响。各影响因素参数取值方案和其正交试验方案如表9所示。

表9 L16(44)正交试验方案设计表Table 9 L16(44)orthogonal test scheme design table

3.2 正交试验结果

根据表9 中的正交试验方案，使用ABAQUS有限元软件建立16 个CRC+AC 复合式路面热力耦合模型，计算在温度和三向非均布荷载耦合作用下沥青层表面和底面的应力，结果如表10所示。

表10 正交试验结果Table 10 Orthogonal test results MPa

3.3 影响因素敏感性分析

3.3.1 极差分析

对正交试验结果进行分析得到4种因素对沥青层表面与底面拉应力与剪应力的极差R，如表11所示。

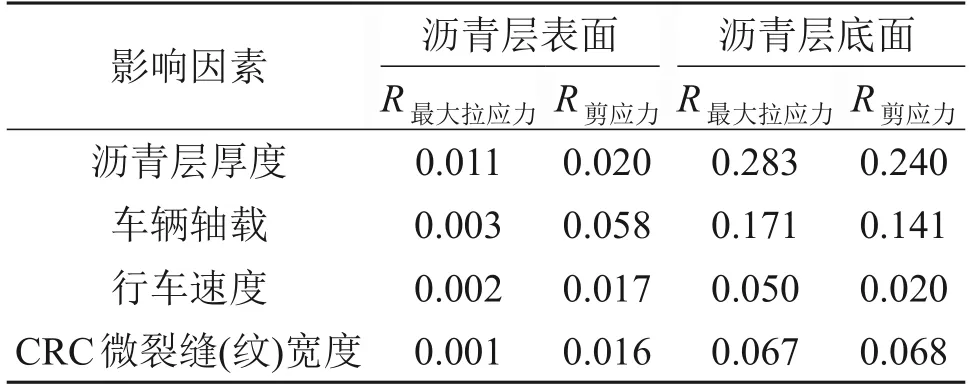
表11 极差R直观分析表Table 11 Visual analysis table of range R

由表11 各因素极差可以看出：对于沥青层表面最大拉应力，影响因素的显著性从大到小依次为沥青层厚度、车辆轴载、行车速度、CRC 微裂缝(纹)宽度；对于沥青层表面剪应力，影响因素的显著性从大至小依次为车辆轴载、沥青层厚度、行车速度、CRC微裂缝(纹)宽度；对于沥青层底面最大拉应力，影响因素的显著性从大至小依次为沥青层厚度、车辆轴载、CRC微裂缝(纹)宽度、行车速度；对于沥青层底面剪应力，影响因素的显著性从大至小依次为沥青层厚度、车辆轴载、CRC微裂缝(纹)宽度、行车速度。这说明沥青层厚度与车辆轴载是主要影响因素。

3.3.2 方差分析

对正交试验结果进行方差分析，利用方差分析软件SPSS进行分析，分析结果如表12所示。在显著性判断中，F越高，代表显著性更大。

表12 方差分析表Table 12 Analysis table of variance

从表12 中各因素的方差可以看出，对于沥青层表面最大拉应力，影响因素的显著性从大至小依次为沥青层厚度、车辆轴载、行车速度、CRC微裂缝(纹)宽度；对于沥青层表面剪应力，影响因素的显著性从大至小依次为车辆轴载、沥青层厚度、行车速度、CRC微裂缝(纹)宽度；对于沥青层底面最大拉应力，影响因素的显著性从大至小依次为沥青层厚度、车辆轴载、CRC 微裂缝(纹)宽度、行车速度；对于沥青层底面最大剪应力，影响因素的显著性从大至小依次为沥青层厚度、车辆轴载、CRC微裂缝(纹)宽度、行车速度。方差分析结果同样表明沥青层厚度与车辆轴载是主要影响因素。方差分析结果与极差分析结果一致，因此，在工程实际中，应该合理设计CRC+AC 复合式路面沥青层的厚度，严格控制车辆超载。

4 结论

1)沥青层厚度是影响沥青层拉应力和剪应力的最主要因素，增加CRC+AC 复合式路面沥青层的厚度可以大幅度降低层底的拉应力和剪应力，减小裂缝病害的产生，但考虑经济性以及厚度过大易产生车辙和提高施工难度，沥青层最佳厚度仍需要综合各种因素进行进一步分析。

2)车辆轴载每增加10 kN，沥青层底拉应力降低10%左右，剪应力约增加14.24%。行车速度每增加10 km/h，沥青层底拉应力约增加2.50%，剪应力约降低1.92%。在低速重载的车辆荷载作用前后，路面层底会产生幅度较大的拉压应力变化，在低速重载下，沥青层受的剪应力也较大，容易导致沥青面层的疲劳开裂的产生与已产生裂缝的扩展，可以通过控制最低行驶速度和车辆超载来延缓沥青层的开裂。

3)随着CRC 层微裂缝(纹)宽度增加，沥青层底面的拉应力和剪应力均大幅增加，裂缝宽度每增加0.1 mm，沥青层底横向拉应力约增加5.02%，纵向拉应力约增加7.51%，剪应力约增加2.56%。对应的沥青层底部容易产生疲劳开裂进而形成反射裂缝，通过合理设计CRC 层配筋率，控制CRC层微裂缝(纹)宽度可以提高道路的使用性能和使用寿命。

4)四因素四水平正交试验的方差分析结果和极差分析结果一致，影响沥青层表面拉应力的因素的显著性从大至小排序为沥青层厚度、车辆轴载、行车速度、CRC微裂缝(纹)宽度；影响表面剪应力的显著性因素从大至小依次为车辆轴载、沥青层厚度、行车速度、CRC微裂缝(纹)宽度；影响底面拉应力的显著性因素从大至小依次为沥青层厚度、车辆轴载、CRC 微裂缝(纹)宽度、行车速度；影响底面剪应力的显著性因素从大至小依次为沥青层厚度、车辆轴载、CRC 微裂缝(纹)宽度、行车速度。沥青层厚度和车辆轴载对沥青层的应力影响最大，对沥青层厚度进行合理设计和控制车辆超载问题可以有效减小裂缝的产生。