含弧形裂隙花岗岩裂纹扩展特征PFC模拟

2023-03-27武世岩黄彦华

中南大学学报（自然科学版） 2023年1期

武世岩，黄彦华,2

(1.中国矿业大学力学与土木工程学院，江苏徐州，221116；2.中国矿业大学深部岩土力学与地下工程国家重点实验室，江苏徐州，221116)

岩体是一种复杂的天然材料，内部含有不同尺度、不同形状的缺陷，如裂隙、孔洞、断层等。在外荷载的影响下，这些存在于岩体中的节理或裂隙会扩展和相互贯通，形成宏观裂纹，导致岩体失稳破坏。研究表明，裂隙的存在会降低岩石的抗压强度，影响岩石的裂纹演化规律[1]。例如，BOBET 等[2]对含预制裂隙类岩石材料试样进行了单轴和双轴压缩试验，总结了翼裂纹和次生裂纹的发育规律。刘红岩等[3]采用水泥、砂和水配制类岩石材料试样，探讨了单轴压缩下节理倾角、节理贯通度、节理组数、载荷应变率、试件长径比、节理充填物厚度及类型对预制节理岩样峰值强度及破坏模式的影响规律。杨圣奇等[4]对断续裂隙大理岩进行了单轴压缩试验，分析了裂隙参数(岩桥倾角、裂隙间距、裂隙长度、裂隙数量与裂隙倾角)对大理岩变形破坏特征的影响规律。郭奇峰等[5]利用水刀切割和金刚石砂线切割技术制备真实花岗岩裂隙试件，探究了单轴压缩下裂隙大理岩裂纹起裂规律、强度特性及破坏模式。在室内试验中，需借助测试系统才能获得应力场、位移场等信息，而数值模拟(如颗粒流程序PFC)则可通过编程较为容易地获得这些数据，因而能够从细观层面揭示岩石裂纹扩展机理。众多研究者通过PFC模拟取得了丰硕的成果。ZHANG 等[6]采用PFC2D对含单裂隙岩样进行了单轴压缩数值模拟，分析了裂纹扩展过程中的应力场演化规律。李勇等[7]运用PFC2D对含2条平行裂隙的红砂岩进行了单轴压缩模拟，分析了试样的裂纹贯通特征。CAO等[8]利用PFC2D对含多条平行裂隙的岩样进行了单轴压缩模拟，总结了裂隙数量和裂隙倾角对峰值强度和破坏模式的影响。黄彦华等[9]使用PFC2D对含断续双裂隙的红砂岩进行了三轴压缩模拟，分析了围压、岩桥倾角等因素对试样裂纹扩展模式和应力分布的影响。

上述研究主要涉及直裂隙对岩石强度及破坏特征的影响。非直裂隙是岩体中常见的天然裂隙，含非直裂隙岩石的力学行为也引起了研究者的关注[10]。董茜茜等[11]对预制直裂隙和“S”型非直裂隙大理岩试样进行单轴压缩试验，分析了直裂隙和“S”型裂隙试件的破坏迹线规律，总结了裂隙参数对岩体的破坏损伤和抗压强度的影响。MA等[12]通过3D 打印制作了含“S”型裂隙的试样，对其进行单轴压缩试验和数值模拟，分析了非直裂隙参数对试样开裂模式和裂纹扩展的影响。YANG 等[13]对含“S”型裂隙红砂岩试样进行了单轴压缩试验和数值模拟，分析并总结了非直线裂隙对试样强度、裂纹扩展和破坏模式的影响。由此可见，目前学者们主要研究了“S”型非直裂隙岩样的宏观力学特性，对其他形状非直裂隙及其细观力学行为的研究还较少。

众多研究表明，含预制裂隙的岩石强度会明显降低，裂隙的形态、长度、位置和倾角对岩石的破坏过程有着重要的影响。弧形裂隙作为一种典型的非直裂隙[14-15]，广泛存在于不同尺度岩石(体)中。然而，有关含弧形裂隙岩样的宏细观力学行为研究还鲜有报道。鉴于此，本文采用颗粒流程序PFC2D构建含弧形裂隙试样的数值模型，探究单轴压缩下弧形裂隙对试样力学特性及裂纹扩展特征的影响规律。首先，基于完整花岗岩试样室内单轴压缩试验结果，标定1组能够反映花岗岩力学特性的PFC 细观参数，并采用含单直裂隙花岗岩试样单轴压缩试验结果进一步验证细观参数的合理性。之后，采用验证的细观参数，构建含弧形裂隙试样的PFC数值模型，进行单轴压缩模拟，分析含弧形裂隙试样应力-应变曲线、力学参数及破裂过程。最后，从应力场角度探讨含弧形裂隙试样的裂纹扩展细观机理。

1 数值模型构建与细观参数验证

1.1 室内试验概况

室内单轴压缩试验使用的试样采自福建省泉州市的花岗岩，主要矿物成分为23.8%(质量分数，下同)的石英、52.4%的钠长石及23.7%的白云母，为细粒至中粒花岗岩，构造致密，孔隙率低，密度约为2 730 kg/m3。试样长×宽×高为80 mm×30 mm×160 mm，采用SANS 岩石力学测试系统进行单轴压缩试验，轴向力在位移控制条件下以1.56×10-5s-1的速率施加到试样上[16]，每种试样类型进行2次实验，数据取平均值。

1.2 PFC模型构建

1971年，CUNDALL 等[17]提出了离散单元法，该方法适用于模拟颗粒之间的运动和相互作用，逐渐发展成为解决复杂固体力学和颗粒流问题的有效工具。在岩石力学方面，PFC可以将相邻的颗粒黏结，形成一个有弹性和破裂特征的集合体，通过不同的受力条件下集合体中颗粒之间的运动以及断裂来模拟岩石的力学行为。在PFC 中，颗粒的运动遵循牛顿第二定律，可以由用户指定墙体的运动。颗粒的生成主要有规则排列、随机分布、外部颗粒导入和块体颗粒组装4种方式，颗粒之间的接触本构模型有刚度模型、接触滑动模型、黏结模型、蠕变模型和遍布节理模型5 种[18]。在PFC中，黏结模型有接触黏结和平行黏结2种。其中，接触黏结模型只传递颗粒间力的作用，而平行黏结模型可以传递颗粒之间力和力矩的作用。研究表明，平行黏结模型更适合模拟岩石类材料[19]。因此，本文数值模拟选择平行黏结模型。

采用PFC 模拟岩样单轴压缩时，首先生成一定数量不同尺寸的圆形颗粒，将其视为模拟单轴压缩试样的刚性体。在试样的垂直方向各设置两面墙，上下两面墙以相同速率朝相反方向运动来模拟单轴压缩试验中的加载板。在达到设定的条件后，墙停止运动，一次模拟结束。

根据花岗岩室内试验结果[16]，在PFC 中生成长×高为80 mm×160 mm 数值模型，试样密度为2 730 kg/m3，共生成14 754 个不同尺度的圆形颗粒，其中包含47 733 个接触(见图1)。颗粒最小半径为0.25 mm，颗粒最大与最小半径之比为2.8。模拟使用位移加载方式，上下加载板以恒定速率进行轴向加载，直至试样破坏。

图1 完整花岗岩试样[16]及PFC数值模型Fig.1 Intact granite specimen[16] and PFC model

1.3 细观参数验证

在进行模拟之前，首先确定模型所需的细观参数。影响平行黏结模型的单元力学参数与接触关系参数主要包括：颗粒接触模量Ec、平行黏结模量颗粒刚度比平行黏结刚度比平行黏结法向强度σn以及平行黏结切向强度τn等。通过以下步骤进行参数标定：首先，调节模型的颗粒接触模量和平行黏结模量，得到与室内试验相近的弹性模量；其次，调节模型的刚度比，得到与室内试验相似的破坏模式；最后，调节平行黏结法向强度与平行黏结切向强度，以获得峰值强度[20]。根据平行黏结模型参数敏感性分析结果[21]，经过“试错法”[22]反复校准，最终得到1组能反映花岗岩室内试验结果的PFC 细观参数，如表1所示。

表1 PFC2D模拟细观参数Table 1 Microscopic parameters in PFC2D

为评价表1所示细观参数的准确性与合理性，将数值模拟与室内试验所得到的应力-应变曲线和破裂模式进行对比，如图2所示。由图2(a)可知，完整试样室内试验测得的单轴抗压强度平均值为100.68 MPa，数值模拟得到的抗压强度为102.65 MPa，两者相对误差为1.96%；弹性模量Es按照应力-应变曲线的30%～70%峰值强度的割线模量取值，室内试验测得的弹性模量平均值为22.46 GPa，数值模拟计算得到的弹性模量为22.56 GPa，两者相对误差为0.45%；由于在PFC中颗粒之间的接触较为紧密，颗粒和与其接触的颗粒数量至少为3个，导致其不能体现出室内单轴压缩试验中出现的初始孔隙压密阶段[18]，因此，数值模拟得到的峰值应变5.12×10-3要略小于室内试验所得峰值应变的平均值5.20×10-3。模拟试样中的宏观裂纹是由不断增加的微裂纹相互贯通形成的。当外力大于颗粒间黏结的承载能力时，颗粒间的黏结断裂，颗粒间的作用力消失，从而产生裂纹[23]。根据断裂形式可以将微裂纹分为拉伸微裂纹和剪切微裂纹，在图2(b)中，红色线段和蓝色线段分别表示拉伸微裂纹和剪切微裂纹。在室内试验中，完整试样呈拉伸破坏，数值模拟试样中的拉伸微裂纹占绝大多数。完整岩样和数值模拟的力学参数和破坏模式对比结果表明，本文所选择的细观参数较为合理。

图2 完整花岗岩试样试验结果与PFC模拟结果对比Fig.2 Comparison of the test results of intact granite specimens with PFC simulation results

为了进一步验证选取细观参数的合理性，对预制单直裂隙试样进行单轴压缩模拟试验，并与相应的室内试验结果进行对比。保持所选取的细观参数不变，删除模型中一定范围内的颗粒预制张开裂隙。由于PFC 模拟生成试样的最小组成部分是刚性颗粒，不能够再被划分，因而预制裂隙边缘较为粗糙。预制裂隙长度为32 mm，裂隙倾角为45°，裂隙中点在试样中心，数值试样的尺寸、预制裂隙长度和倾角均与室内试验时保持一致。

图3所示为预制单直裂隙试样室内试验与数值模拟结果对比。预制单直裂隙试样室内试验测得的单轴抗压强度平均值为75.81 MPa，数值模拟计算得到的抗压强度为73.65 MPa，两者相对误差为-2.85%；预制单裂隙试样室内试验测得的弹性模量平均值为21.46 GPa，数值模拟计算得到的弹性模量为20.67 GPa，两者相对误差为-3.68%，数值模拟的峰值应变3.83×10-3要小于室内实验值的平均峰值应变4.13×10-3。在单直裂隙试样的室内单轴压缩试验中，出现的裂纹可以分为翼型裂纹和次生裂纹[2]。从图3(b)可以看到，数值试样的破坏形式和裂纹特征与室内试验结果基本相同，说明选取的细观参数能很好地模拟含单直裂隙花岗岩的破坏特征。

图3 含单裂隙花岗岩试样试验结果与PFC模拟结果对比Fig.3 Comparison of the test results of granite specimens containing a single fissure and PFC simulation results

单直裂隙试样模拟得到的应力-应变曲线、力学参数和宏观破坏模式与室内试验结果较一致，进一步验证了表1所示细观参数的合理性。因此，可以采用表1中的细观参数对含预制弧形裂隙花岗岩试样进行单轴压缩模拟试验，然后对其力学特性和裂纹扩展特征进行分析。

2 弧形裂隙花岗岩宏观力学行为

为分析预制弧形裂隙花岗岩在单轴压缩下的力学行为特征和裂纹扩展规律，设计了如图4所示的裂隙分布形式。其中，裂隙长度L=32 mm，与单直裂隙长度相同；宽度D=2.0 mm；裂隙形状为半椭圆，椭圆的中心固定为试样中心，椭圆的半长轴长度为a，半短轴长度为b，长短轴比γ=b/a。当γ由直裂隙逐渐过渡至弧形裂隙时，保持裂隙的总长度不变，分别探究不同裂隙倾角α(0°，45°和90°)和不同长短轴比γ(0，0.2，0.4，0.6，0.8和1.0)对含弧形裂隙花岗岩力学行为的影响规律。

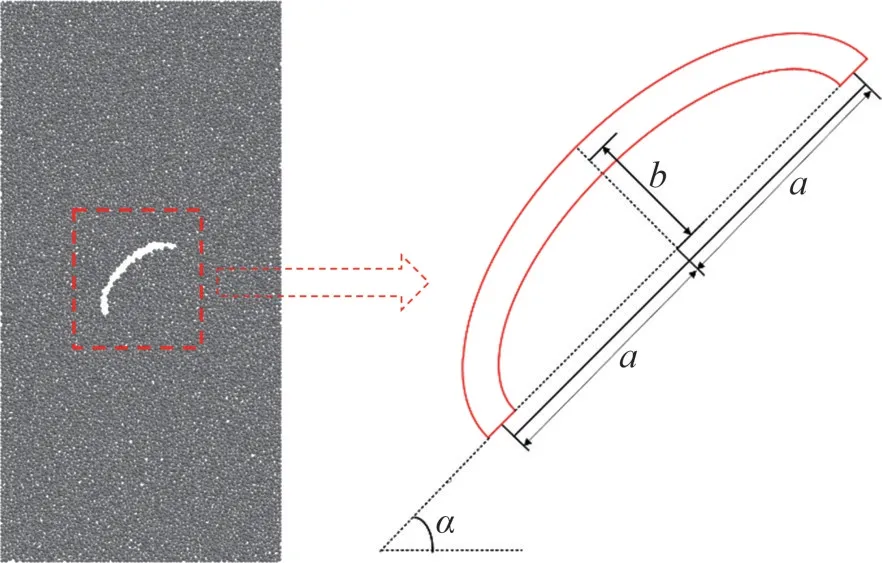
图4 弧形裂隙试样几何参数示意图Fig.4 Geometric parameters diagram of specimen containing an arc fissure

2.1 力学参数特征分析

图5所示为单轴压缩下弧形裂隙花岗岩应力-应变曲线。由于PFC不能体现初始孔隙压密阶段，模拟获得的应力-应变曲线初始阶段为弹性变形阶段，应力随应变呈线性增大。随着轴向应变逐渐增加，应力-应变曲线逐渐由线性转为非线性，并在峰后出现明显跌落。由图5可见，裂隙试样的抗压强度均比完整试样的小，裂隙倾角α和长短轴比γ对试样的峰值强度和弹性模量有明显的影响。

图5 单轴压缩下弧形裂隙花岗岩试样应力-应变曲线Fig.5 Stress-strain curves of granite samples containing an arc fissure under uniaxial compression

为进一步分析裂隙倾角α和长短轴比γ对弧形裂隙试样力学参数的影响，分别研究含弧形裂隙花岗岩峰值强度σs和弹性模量ES与裂隙倾角α和长短轴比γ的关系，结果见图6。由图6 可见：当裂隙倾角α为0°时，随着γ从0增大到1.0，保持预制裂隙长度不变，σs由50.97 MPa 逐渐增大到69.44 MPa，弹性模量Es也从16.41 GPa逐渐增大到20.06 GPa。这可能是由于在γ增大过程中，弧形裂隙在水平方向的投影长度从32.00 mm 减小至20.37 mm，对试样造成的损伤减小。

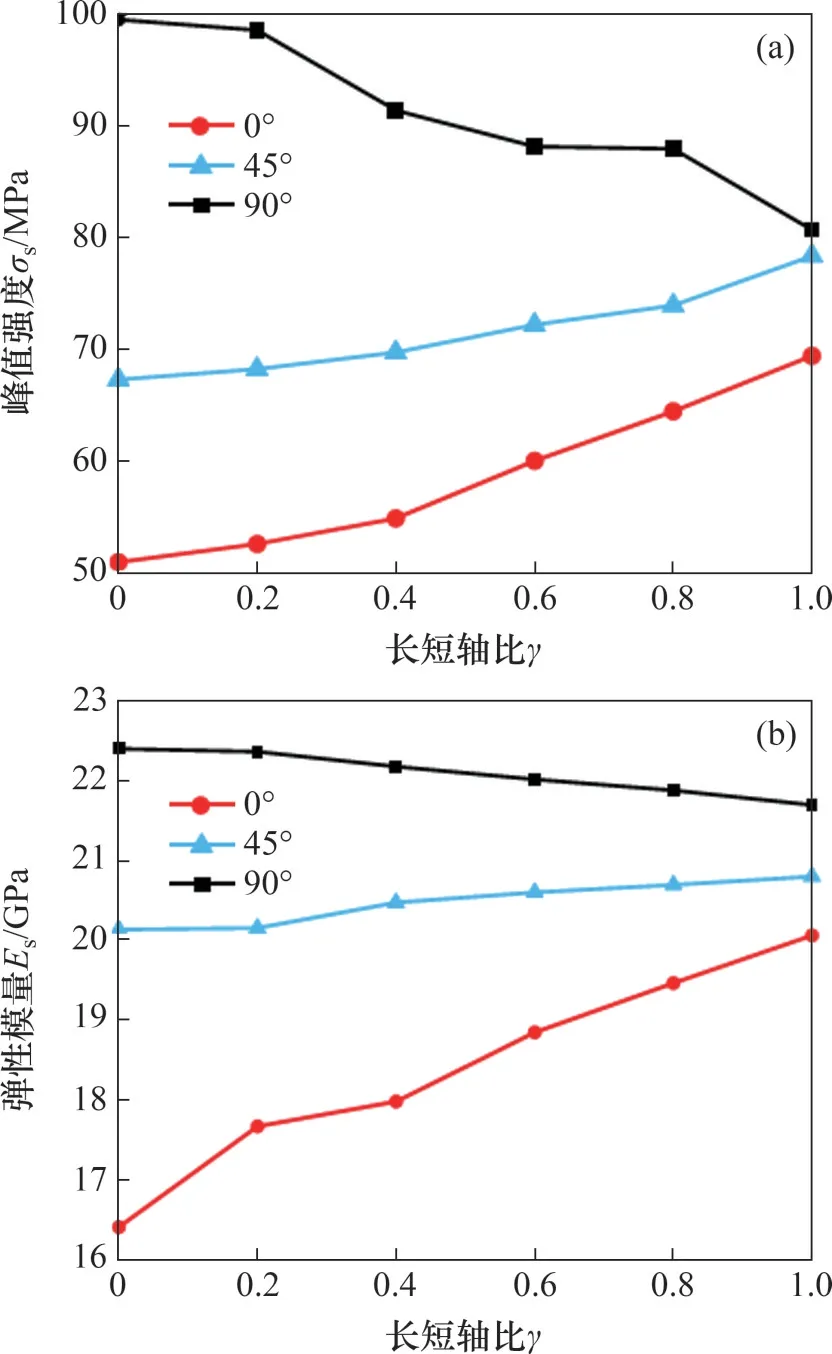
图6 裂隙参数对弧形裂隙花岗岩力学参数的影响Fig.6 Effect of fissure geometry on mechanical parameters of granite specimens containing an arc fissure

当裂隙倾角α为45°时，随着γ从0增大到1.0，峰值强度σs由67.32 MPa 逐渐增大到78.38 MPa，弹性模量Es也从20.13 GPa 逐渐增大到20.79 GPa。与裂隙倾角0°试样相同，此时弧形裂隙在水平方向的投影长度随γ的增大而减小，从22.62 mm 减小至17.39 mm。

当裂隙倾角α为90°时，随着γ从0增大到1.0，峰值强度σs由99.53 MPa 逐渐减小到80.72 MPa，弹性模量Es也从22.39 GPa 逐渐减小到21.69 GPa。与裂隙倾角0°和45°试样不同的是，此时，弧形裂隙在水平方向的投影长度随γ的增大而增大，从1.00 mm 增大至10.19 mm。当裂隙倾角α为90°，γ=0即裂隙为直裂隙时，预制裂隙试样和完整试样的峰值强度σs相对误差为3.03%，弹性模量Es相对误差为0.740%，说明此时的预制裂隙对试样的力学特性影响很小。由此可见，预制裂隙的水平投影长度对试样的力学性质有很大影响，投影长度越大，峰值强度σs和弹性模量Es相对越小，并且随着长短轴比γ的增大，含不同倾角裂隙试样的力学参数差值逐渐减小。

2.2 宏观裂纹扩展模式分析

在模拟试样中，除了有微裂纹相互贯通产生的宏观裂纹外，还会有部分小而分散的微裂纹。这些小而分散的微裂纹对试样的破坏模式影响不大[18]，因此，本文主要分析宏观裂纹对破坏模式的影响。

在含弧形裂隙的试样中，裂纹主要是从预制裂隙的上、下尖端开始萌生，并且与预制裂隙的角度和形状有着密切的关系。结合已有的裂纹扩展研究成果[24]，将模拟中的裂纹从翼型裂纹和次生裂纹细分为以下5种类型，其中4种类型为拉伸裂纹(分别命名为Tw，Ts，Ta，Tas)，1 种类型为远场裂纹(Fc)，如图7所示。

图7 弧形裂隙试样不同类型裂纹示意图Fig.7 Sketch of different crack types of granite specimens containing an arc fissure

1)Tw型裂纹。从预制裂隙尖端或距尖端一定距离处开始起裂，沿着曲线路径扩展，之后沿着主应力方向发育，通常称为“翼裂纹”[25]。

2)Ts型裂纹。这种拉伸裂纹在Tw型裂纹发育之后开始出现，通常从已有Tw型裂纹扩展的端点处或Tw型裂纹扩展路径上开始起裂，与同一点处萌生的Tw型裂纹扩展方向大致相同，沿主应力方向向试样端面发育。

3)Ta型裂纹。扩展方向与Tw型裂纹扩展方向相反的拉伸裂纹，通常称为“反翼裂纹”[26]。大多数Ta裂纹从预制裂隙尖端处开始起裂，沿着主应力方向扩展。

4)Tas型裂纹。通常在Ta型裂纹发育之后开始萌发，从已有Ta型裂纹扩展的端点处或Ta型裂纹扩展路径上开始起裂，通常沿着主应力方向扩展。

5)Fc型裂纹。不是从预制裂隙尖端或裂纹扩展路径上萌发的裂纹，可能垂直或平行于主应力方向扩展。

根据以上裂纹分类，对预制弧形裂隙试样的单轴压缩模拟进行分析，可以发现试样的破坏模式是这几种裂纹的共同作用的结果。图8～10所示为不同裂隙倾角试样的裂纹扩展过程，其中，试样起裂强度定义为裂纹数达到峰值强度σs裂纹数的1%时所对应的主应力[27]，数字表示裂纹扩展顺序，字母表示同一时刻不同位置产生的裂纹。

图8所示为裂隙倾角α=0°，γ=0.4 的试样宏观裂纹的发育过程和不同长短轴比γ的弧形裂隙试样的破坏模式。以γ=0.4 的试样为例，当轴向应力σ1为7.80 MPa 时，预制裂隙左下端和右下端先后萌生出Tw型裂纹1a和1b，其中裂纹1b在整个加载过程中发育较慢。当σ1=14.11 MPa 时，从预制裂隙的上尖端发育出Tw型裂纹2。当σ1增大至36.31 MPa 时，裂纹1a和2 发育速度开始放缓。随着轴向应力增加到50.75 MPa(92.4%σs)，Ta型裂纹3a、Tas型裂纹3b、Ta型裂纹3c、Fc型裂纹3d和Ts型裂纹3e出现，直至σ1=51.94 MPa时，裂纹3a发育至试样上端面，随后在σ1=52.94 MPa 时裂纹3d发育至试样下端面。当σ1=54.66 MPa 时，在裂纹3c的发育处萌生出Tas型裂纹4。直到峰值应力出现后，当轴向应力σ1跌落至47.99 MPa时，在试样中产生Fc型裂纹5。

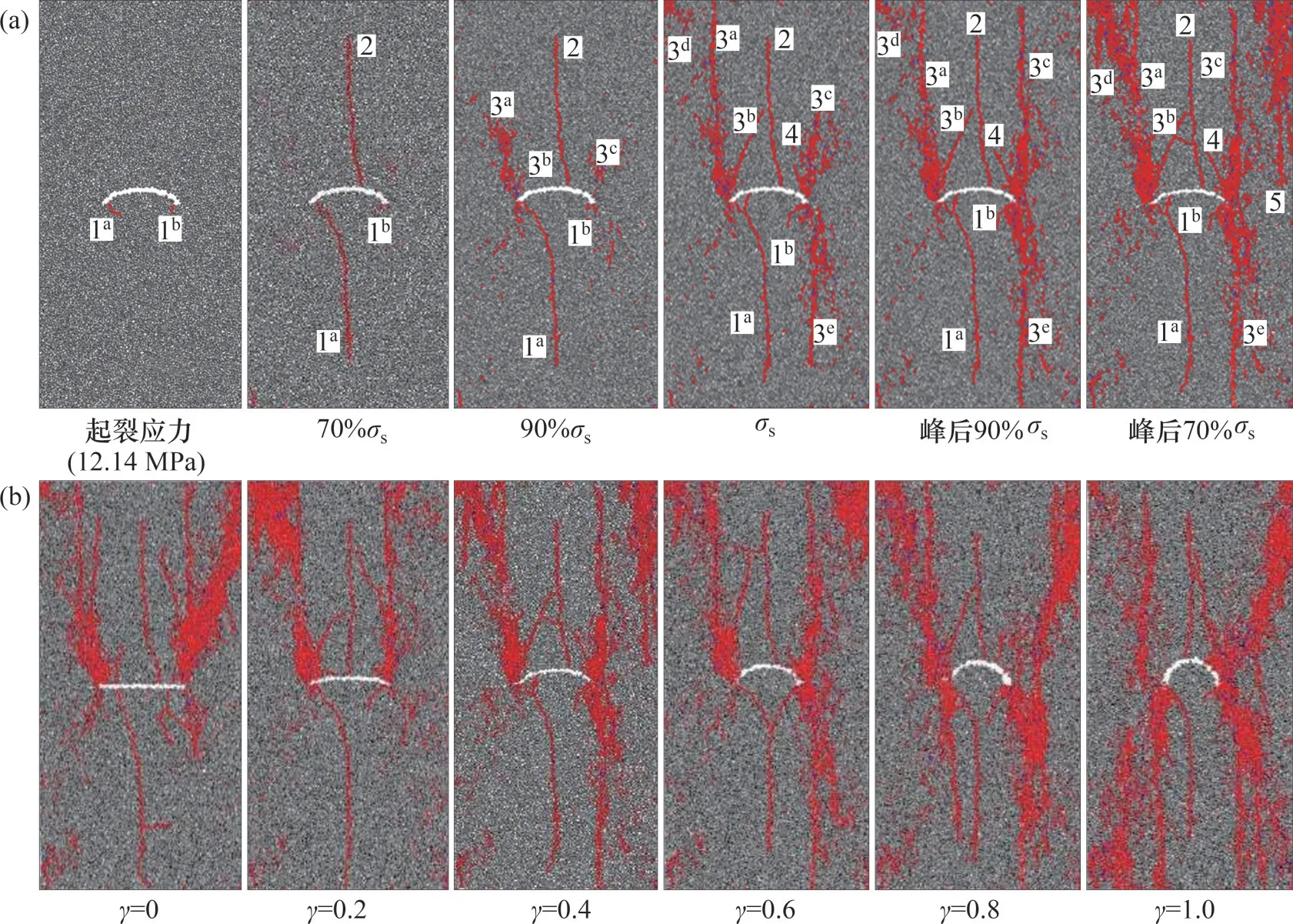
图8 弧形裂隙花岗岩试样裂纹发育过程和宏观破裂模式(α=0°)Fig.8 Fracture processes of granite specimen containing an arc fissure and failure modes of granite specimens(α=0°)

当裂隙倾角α=0°时，除了γ=0即预制裂隙为直裂隙的试样，其他试样的初始翼裂纹都从预制裂隙的左、右两端产生，且2条初始翼裂纹中的一条裂纹的扩展速度和长度明显比另1 条的低。之后，在预制裂隙上尖端会萌生第3条拉伸裂纹，沿主应力方向发展。当轴向应力加载到55.75%σs(γ=0.2)～72.88%σs(γ=1.0)范围时，初始翼裂纹和第3 条拉伸裂纹发育速度放缓，之后开始出现次生裂纹。在γ=0 和0.2 的试样中没有出现Ts型裂纹，随着γ增加，Ts型裂纹的长度逐渐增加，Fc型裂纹的数量和宽度增大。在γ=0.4～1.0 的试样中都出现次生裂纹与从预制裂隙上尖端萌生的Tw型裂纹相互贯通的情况，只有在γ=0.6 的试样中有裂纹连接2 个裂隙尖端。由此可见，随着长短轴比γ的增加，预制裂隙对裂纹类型的影响逐渐降低，次生裂纹的数量和扩展程度增大。

图9所示为裂隙倾角α=45°，γ=0.4的试样宏观裂纹的发育过程和不同长短轴比γ下弧形裂隙试样的破坏模式。在γ=0.4 的试样中，Tw型裂纹1a和1b分别在σ1=12.53 MPa和14.55 MPa时从预制裂隙左下端和右上端萌发，至σ1=54.54 MPa时2条裂纹发展速度减慢。在σ1=62.38 MPa和67.42 MPa时，预制裂隙左边和右上端出现Fc型裂纹2 和Ta型裂纹3a，2 条裂纹快速发育，裂纹2 与预制裂隙左端连通，之后Tw型裂纹 3b、Tas型裂纹3c、Ts型裂纹3d、Fc型裂纹3e这4 条次生裂纹出现。到σ1=69.03 MPa时，裂纹2 贯通至试样上端面，随后试样加载至峰值强度。在轴向应力从69.68 MPa 下降到69.26 MPa 的过程中，依次产生Ts型裂纹4a、Fc型裂纹4b、Tas型裂纹4c。到σ1=67.82 MPa时，Ta型裂纹3a贯通至试样下端面。在应力下降到59.34 MPa之后，Fc型裂纹5a、Tas型裂纹5b在试样中出现。

图9 弧形裂隙花岗岩试样裂纹发育过程和宏观破裂模式(α=45°)Fig.9 Fracture processes of granite specimen containing an arc fissure and failure modes of granite specimens(α=45°)

在长短轴比γ=0，0.2 和0.4 的3 个试样中，初始翼裂纹都是在预制裂隙端点萌生，并且在峰值强度左右可以观察到有微裂纹从预制裂隙中段萌生，而在γ=0.6，0.8 和1.0 的3 个试样中，右侧的初始翼裂纹的起裂位置从预制裂隙端点转移到主应力方向的裂隙上尖端，在预制裂隙中段也没有微裂纹产生。在γ=0.4～1.0 的试样中，在预制裂隙左端不再产生Ta型裂纹，而是先在预制裂隙旁边萌生出Fc型裂纹，逐渐连通到预制裂隙，之后在连接处发育出Tas型裂纹，且随着γ增大，Fc型裂纹的数量逐渐增加。在轴向应力加载至峰值应力左右(98.01%σs～峰后92.40%σs)，6 个试样都有次生裂纹贯通至试样端面。由此可见，随着长短轴比γ增大，试样中裂纹的起裂位置逐渐发生改变，贯通至端面的裂纹逐渐增多，裂纹数量逐渐增加。

图10所示为裂隙倾角α=90°，γ=0.4 的试样宏观裂纹的发育过程和不同长短轴比γ下的弧形裂隙试样的破坏模式。以γ=0.4 的试样为例，当σ1为20.20 MPa 和25.96 MPa 时，预制裂隙上端和下端先后萌生Tw型裂纹1 和2。当轴向应力增大至64.62 MPa 时，在预制裂隙中段产生Ts型裂纹3。到σ1=78.23 MPa 时，在试样左上端萌生出Fc型裂纹4a。当σ1=81.97 MPa时，从预制裂隙下端点萌生出Ta型裂纹4b，沿着主应力方向发育，至σ1=84.57 MPa 时连通预制裂隙两端。当σ1=85.58 MPa时，在试样右上部分萌生出Fc型裂纹5。在峰值应力出现后，当应力下降到91.28 MPa时，在试样左下端产生Fc型裂纹6a，随后在试样左上部分萌生出Fc型裂纹6b。

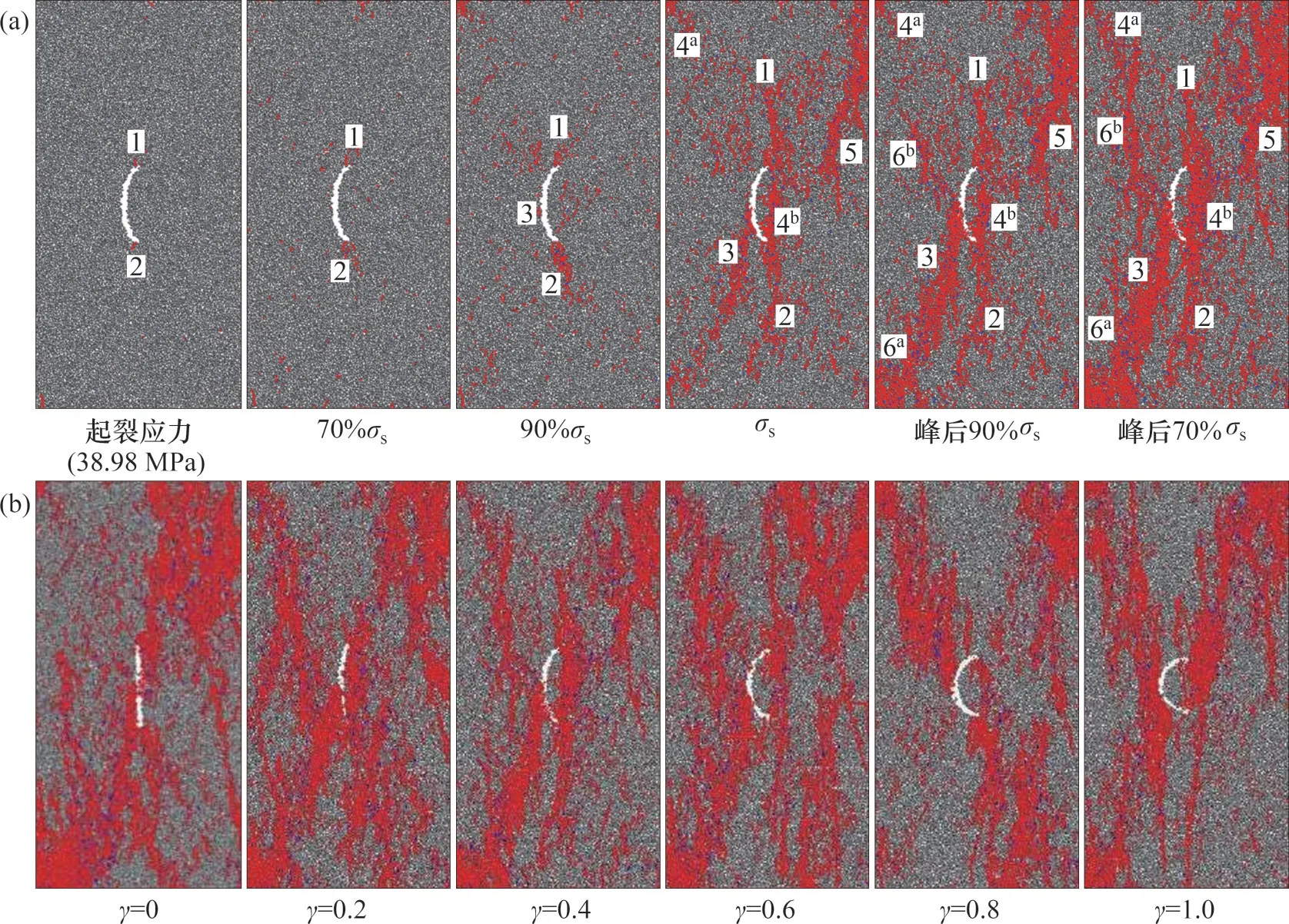
图10 弧形裂隙花岗岩试样裂纹发育过程和宏观破裂模式(α=90°)Fig.10 Fracture processes of granite specimen containing an arc fissure and failure modes of granite specimens(α=90°)

除直裂隙试样以外，含弧形裂隙试样中均出现连通预制裂隙端点的裂纹，在峰值强度附近都没有出现裂纹扩展至试样端面的情况。由此可见，当弧形裂隙在试样中垂直分布时，长短轴比γ对试样的裂纹特征影响较小。

此外，由图8～10 可见，裂隙倾角α对含弧形裂隙试样破裂特征有较为明显的影响。在长短轴比γ相同的情况下，随着裂隙倾角的增大，预制裂隙的水平投影长度逐渐减小，试样中Ts型、Tas型裂纹的数量逐渐减少，Fc型裂纹的数量逐渐增加。对比试样的破裂模式可以看到，随着裂隙倾角α增大，试样内裂纹的整体宽度逐渐增大，裂纹间贯通情况更为明显，并且微裂纹的聚集程度逐渐减小，出现了更多分布在整个试样内的小微裂纹，试样的破坏程度逐渐增大。

3 弧形裂隙花岗岩细观力学行为

试样微裂纹的产生、扩展和贯通对岩石材料宏观断裂损伤有重要的影响。PFC可以记录模拟过程中微裂纹的分布和数量、接触力场等信息。图11(a)所示为当裂隙倾角α为45°时，不同长短轴比γ的预制裂隙试样裂纹起裂前(即试样内未出现微裂纹，为方便比较，取各试样轴向应力为7.5 MPa的情况)力链分布。图11中，红色代表拉伸力链，黑色代表受压力链。由图11(a)可以看到，随着长短轴比的增加，预制裂隙右上角的拉应力集中区逐渐向裂隙中部偏移，左下角的拉应力集中区沿着裂隙下端面逐渐向右延伸。而裂隙左边的压应力区逐渐从集中在裂隙端点变为分布在裂隙左边。因此，试样的最初裂纹产生的位置从裂隙端点变为裂隙上尖端，在裂隙左端点也逐渐不再产生向试样上端发育的次生裂纹，出现了连通预制裂隙两端的次生裂纹。

图11 弧形裂隙试样裂纹起裂前力链分布(σ1=7.5 MPa)Fig.11 Force chain distribution of granite specimen containing an arc fissure before cracks initiation(σ1=7.5 MPa)

图11(b)所示为当γ=0.4 时，不同裂隙倾角α的预制裂隙试样起裂前的力链分布。由图11(b)可以看到，随着裂隙倾角的增大，拉应力集中区的面积逐渐减小，分布范围从沿预制裂隙分布向预制裂隙端点集中，而在α=90°的试样中，拉应力和压应力集中区都很小，只在裂隙端点可以看到明显的拉应力集中，这种情况对试样产生的影响最小。由此可见，随着裂隙倾角α增大，预制裂隙对试样的裂纹特征和破裂模式的影响逐渐减少。

图12所示为当裂隙倾角α为45°、长短轴比为0.4 时，含弧形裂隙试样的应力与微裂纹总数的关系以及对应的力链特征。图12 中，红色代表拉伸力链，黑色代表受压力链，蓝色代表微裂纹。在A点时，对应轴力为20.93 MPa(30%σs)，轴向应变为1.04×10-3。此时试样处于弹性变形阶段，Ts型裂纹1a和1b正在快速发育，可以看到在2条裂纹的顶端出现拉应力集中区，试样内共产生60条微裂纹。随着轴向应变的增加，到B点时，主应力为62.81 MPa(90%σs)，轴向应变为3.12×10-3，这时，试样已经进入塑性变形阶段，裂纹1a和1b发育放缓，Fc型裂纹2开始向试样上端沿发育，试样内共产生803条微裂纹，微裂纹数开始快速增长。至C点时，主应力增大到67.66 MPa(97%σs)，轴向应变为3.45×10-3，微裂纹相互贯通形成Ta型裂纹3a，向试样下端发育。可以看到，此时预制裂隙左边的压应力区面积缩小，裂隙右上端和翼裂纹形成拉应力集中区，裂隙下边面的拉应力增大。在峰值应力D处，主应力为69.76 MPa，轴向应变为3.61×10-3，次生裂纹3b从拉应力较为集中的预制裂隙下边面萌生出来。随着反翼裂纹3a的发育，从裂纹3a中段发展出Tas型裂纹3c，而在预制裂隙的右端点也发育出Ts型裂纹3d，裂纹3d与1b之间有明显的拉应力集中，试样内共有2 568条微裂纹。在峰值应力出现后的E点，轴向应力下降至68.36 MPa(峰后98%σs)，轴向应变增大到3.80×10-3，从裂纹2和预制裂隙的连接处萌生出发育速度较快的Tas型裂纹4a，在试样中产生Fc型裂纹4b和次生反翼裂纹4c，而由于Ts型裂纹3d和裂纹1b相互贯通，2条裂纹之间不再出现拉应力集中现象，预制裂隙下边面的拉应力集中程度也随着裂纹3b的发育而减弱，此时，微裂纹达到3 567条，预制裂隙左右的压应力区面积明显减小，从预制裂隙及其周围萌发的裂纹都已出现。

图12 α=45°，γ=0.4时裂隙试样细观力场演化和微裂纹扩展Fig.12 Meso-force evolution and microcrack propagation in granite specimens containing an arc fissure when α=45° and γ=0.4

到峰后阶段F点时，对应的轴向应力为55.81 MPa(峰后80%σs)，轴向应变为4.31×10-3，共产生6 121条微裂纹，这时，试样的宏观破坏模式已经形成，沿着部分成型裂纹出现拉应力集中现象，使得在一些宏观破坏模式相似的试样中出现连通相邻平行裂纹的横向裂纹。通过上述分析可以看到，在裂纹扩展的初期，试样中的拉应力集中区从预制裂隙尖端转移至翼裂纹端点。随着试样进入塑性变形阶段，在裂纹和预制裂隙的连通处逐渐出现拉应力集中的情况，之后这些地方萌生出次生裂纹。峰值应力出现之后，沿着已经发育的裂纹形成拉应力集中区，产生出连通宏观裂纹的横向微裂纹。