基于向量式有限元的岸边集装箱起重机地震响应分析

鲍帅函 林伟华 刘 龙 王嘉诚

1上海海事大学物流工程学院 上海 201306 2上海振华重工（团）股份有限公司 上海 200125

0 引言

岸边集装箱起重机（以下简称岸桥）是专门用于集装箱码头对集装箱船进行装卸作业的专业设备，一般安装在港口码头岸边。随着港口物流行业的发展，为满足大型化的集装箱船舶的装卸作业，岸桥也在向大型化发展，但大型岸桥结构重心高、侧向刚度不均，在地震作用下也更容易不稳定。此外，岸桥结构生产周期长且成本高，若在地震中遭到严重破坏，对其进行维修的花费时间和经济成本都将非常高。我国是一个地震多发的国家，所以对地震激励下的岸桥进行分析十分很有必要。

在目前的研究中针对地震作用下的起重机响应研究方面，周鹏等[1]将功率谱作为地震输入，分析了岸桥在不同工况下受到地震激励时的结构响应；Sun Y G等[2]基于 ADAMS 建立岸桥模型，计算了起重机在地震波激励下的动力响应；Feau C等[3]通过比例为 1/5 的起重机桥架模型进行地震试验；Azeloglu C O等[4]建立了地震荷载作用下的起重机动力学模型，用振动台试验结果对模型进行验证；路世青[5]进行了地震下结构弹塑性分析，采用多种地震波分别激励得到地震过程中的结构响应结果；Yao G等[6]分析了悬臂塔式起重机的地震反应和动力特性，说明在地震激励下的起重重物在一定程度上可视为惯性阻尼，为了模拟起重机的跳轨现象，使用摩擦接触模型来模拟起重机车轮与轨道之间的作用；Jacobs L D等[7]建立了二维和三维岸桥模型，通过试验和仿真分析说明二维岸桥模型即可表现出三维模型在地震作用下的结构跳轨现象，大车运行方向的结构扭转对结果的影响很小，可以忽略；Nguyen V B等[8]建立了1/20的岸桥缩尺模型进行振动台试验，试验证明摩擦接触模型可以较准确地模拟车轮与轨道的接触作用；李哲等[9]进行了振动台试验，验证了岸桥跳轨临界加速度计算的准确性，说明只对结构施加小车方向地震波便可模拟地震激励下的结构运动结果。

在现有研究基础上，本文用向量式有限元的方法分析岸桥在地震下的动力学响应。首先对岸桥的铰接节点和耦合单元进行分析，定义了节点和单元的受力公式，提出改进的轮轨接触模型并验证。对整个岸桥建立向量式有限元模型，而后又对地震下的岸桥跳轨行为进行分析。

1 向量式有限元理论

1.1 基本理论

向量式有限元由3个基本理论组成，分别为点值描述、途径单元和虚拟的逆向运动[10，11]。点值描述指在空间上将结构描述为一群质点的集合，质点间采用单元连接，单元没有质量，只承受内力。质点的运动满足牛顿第二定律，每个质点的质量按照质点的位置赋予其对应结构的质量。

在时间上将运动历程划分为一组时间点，时间点之间的过程用一组控制方程计算，这组方程被称为途径单元。使用一组相互连接的途径单元来描述构件随时间运动的目的是为了简化内力计算和处理不连续行为。控制方程是一组点的运动与位移公式，在计算质点间内力的同时亦描述出内力与质点的位置之间的关系。为了用质点的运动来描述构件的运动过程，需要计算空间点之间相互作用的内力。杆单元的内力计算公式与位移迭代公式为

梁单元的内力计算公式与位移迭代公式为

1.2 铰接节点

为使岸桥前大梁在非工作状态下抬起，前大梁与后大梁通过铰接方式连接。为了模拟出铰接2单元的相对转动，需要对单元的内力计算公式进行修改。假设单元1-2为梁单元，常见的刚接节点单元两端的节点内力计算公式为

假设梁单元2-3中节点3为铰接点，由铰接结构的性质可得

将式（6）代入式（5）可得与铰接点连接的单元2-3两端节点的内力计算公式为

综合以上为存在铰接节点时的向量式有限元计算方法，在具体编程中需要先判断节点为铰接还是刚接，之后选择各自对应的内力计算公式进行计算。

1.3 梁杆单元耦合

岸桥的主体使用梁单元来构建，但结构中的拉杆不承受弯矩作用，故需使用杆单元进行构建。对于同时连接杆单元与梁单元的节点，如何正确描述不同单元间的耦合作用是需要解决的问题。

假设单元1-2、单元2-3为梁单元，单元2-4为杆单元，即节点2与2个梁单元和1个杆单元相连接，对节点2所受的单元内力进行分析。由式(1)可得杆单元2-4传递给节点2的内力为

式中：Δ24为单元2-4的纯变形，l24为单元2-4的长度，x2n、x4n和y2n、y4n为节点2和节点4在tn时刻的水平和竖直位置坐标。

由梁单元的内力计算公式可得，梁单元1-2和单元2-3传递给节点2的内力为

式中：Δ12和Δ23为单元1-2和单元2-3的纯变形，l12和l23为2个单元的长度，φ12和φ21为单元1-2上节点1与节点2的转角，φ23和φ32为单元2-3上节点2与节点3的转角。

至此，得到各单元作用在节点2上的内力，由于内力均按照坐标轴进行分解，故可得节点2受到的总内力为

由此，在程序求解过程中先通过单元受力情况对单元的类型进行判断，将处于耦合单元位置的节点的内力计算公式进行替换，至此便完成单元耦合问题的分析。

2 轮轨接触的改进模型

对于结构与轨道的接触行为模拟主要有接触的识别和接触的作用力加载2点，目的分别是确定目标是否发生接触和确定接触力的大小和方向。

岸桥轮轨边界接触模型如图1a所示，车轮的两侧存在轮缘，轮缘与轨道之间存在间隙，若按照实际的轮轨接触进行设置会导致计算困难且效率降低，以往学者将轮轨接触简化为如图1b所示铰接模型和如图1c所示摩擦接触模型。其中，铰接模型的设置方法为释放约束位置节点的旋转自由度，由相关文献可得铰接约束设置可准确地模拟出地震作用下的结构运动，但铰接模型无法模拟出结构的跳轨和脱轨行为。摩擦接触模型的设置方法为根据结构的运动给予其水平方向上的摩擦力和垂直方向上的接触力，可以模拟出结构与轨道的分离。

图1 轮轨边界约束模型

在实际跳轨后，结构会在自重的作用下回落并与轨道发生碰撞，此时若没有对节点施加对应的约束会导致节点穿过接触面，不符合实际的情况，故需考虑接触的识别和并施加相应接触力。

如图2所示，假设δ为岸桥陆侧门腿底端车轮（节点1）与轨道顶端的垂直距离，当车轮发生抬腿时δ＞0，车轮与轨道之间没有力的作用。y1和yT分别为节点1和轨道T的垂直方向坐标，nT为轨道的法向向量，结构与轨道发生接触的判定公式为

图2 点与面的接触示意图

当δ≤0时说明结构与轨道发生接触，此时需要对节点1施加对应的接触力。岸桥与轨道发生接触后，假设节点1沿水平方向（小车运行方向）的速度为vt，则岸桥在接触位置受到的接触力表达式为

式中：Fn为法向接触力，Ft为摩擦力，k为竖向接触弹簧刚度，μ为摩擦系数。

3 岸桥模型的建立

3.1 岸桥模型的点值描述

根据相关研究可得地震作用下的岸桥结构运动主要由小车运行方向的地震波导致，大车运行方向上的结构运动可以忽略，使用二维模型便可模拟出结构的运动，故建立二维的岸桥模型进行分析。在Ansys软件中建立有限元模型，起重机的主体结构用23个Beam 188单元构建，拉杆结构用5个Link 180单元构建，质量点使用21个Mass 21单元施加在对应位置上。

如图3所示，建立对应的基于向量式有限元理论的点值描述模型。基于向量式有限元的特性只选择结构的关键位置设置节点，图中表示出了节点的编号，y方向为垂直方向，x方向为小车运行方向。拉杆结构用杆单元构建，其他结构用梁单元构建，不同位置节点的惯性矩和截面面积等参数按照实际的截面尺寸进行计算获得。不同位置单元的材料特性按照实际模型设置，将简化后无法表示的部分结构通过增加单元密度的方式来模拟其对结构的作用，将机器房等结构视为质量点施加在对应位置上，质量点施加位置与质量大小如表1所示。

图3 岸桥点值描述示意图

表1 施加质量点的节点编号与质量大小

3.2 接触模型验证

如图4所示，使用接触识别和施加接触力的方法模拟轨道与岸桥的接触。参照相关文献取弹簧刚度为4.375×109N/m，取节点1的位置为坐标原点，岸桥结构重心G的水平坐标为24.424，即重心与陆侧门腿的水平距离l1为24.424 m，与海侧门腿的水平距离l2＝30.48-24.424＝5.939 m，L为岸桥的基距，R1与R4为节点1和节点4所受的支反力。只考虑结构自重的作用，根据重心的位置和整机质量可得R1约为1 355 508.34 N，R4约为5 466 799.17 N。将支反力的值代入式(13)中的法向接触力计算公式中可得陆侧与海侧门腿底部与轨道接触导致的垂直位移δ1和δ4分别为-3.098×10-4m和-1.250×10-3m。

图4 岸桥与结构重心示意图

使用向量式有限元编程进行计算，图5所示曲线稳定后垂直方向上节点1的位移为-3.090×10-4m，节点4的位移为-1.250×10-3m。与理论计算得到的数值相比，位移误差分别为0.26%和0.00%。由此可知，通过施加接触力的方法可有效模拟接触导致的位移。

图5 自重作用下的节点位移

4 地震下的跳轨行为分析

假设小车在后大梁上的节点12位置处静止，选取地震波对结构进行加载，所选地震波为EI Centro地震波（美国），地震波的相关参数如表2所示。将所有地震波都进行相同的线性插值处理，从起始位置时间开始将选取的各个地震波沿小车运行方向和垂直方向加载在结构上。

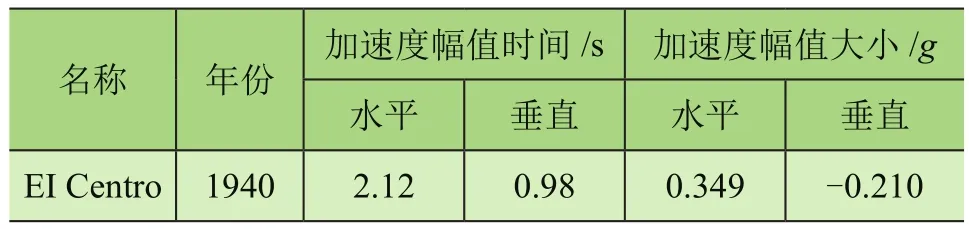
表2 地震波参数

岸桥大车的车轮轮缘与轨道之间存在卡夹作用，且在强地震激励下岸桥会发生抬腿和脱轨现象，所以在目前相关研究中会设定摩擦系数取一个较大值来模拟轮缘与轨道之间的接触作用，取值范围为0.7～0.9，取摩擦系数为0.9，不对节点的水平方向位移进行约束。

选EI Centro地震波作用下的结构运动进行分析，选取2.753 s、5.604 s、7.71 s和18.28 s这4个时刻的整机位移，将位移放大40倍得到的结果如图6所示。由结果可知，在地震波的作用下结构在水平方向上出现位移，陆侧门腿在抬腿的同时也发生了脱轨现象。海侧门腿虽未发生抬腿但发生了脱轨，这与结构的重心位置相关，由于海侧门腿与重心的水平距离较近，与陆侧门腿相比难以发生抬腿现象。

图6 不同时刻对应的整机位移示意图

选取后大梁最远端（节点10）与前大梁最远端（节点21）的节点进行分析，位移结果如图7所示。由图7可知，大梁上的位置在水平方向上的位移结果差距不大，而垂直方向上的位移差距较明显，这与结构特征与陆侧门腿的抬升有关。

图7 大梁上不同位置的节点位移

选取海侧门腿与下连接梁的连接位置（节点5）、海侧门腿与大梁的连接位置（节点16）与结构最高位置（节点9）进行分析，位移结果如图8所示。由图8可知，不同高度的位置在水平方向上的位移结果差距不大，高度越高的位置在垂直方向上的位移幅度越大。

图8 不同高度位置的节点位移

5 结语

本文首先基于向量式有限元理论建立了岸桥模型，说明对结构中的耦合单元、铰接点等特征的表示方法。使用向量式有限元理论设置小车与岸桥的轮轨摩擦接触模型，提出一种地震激励下的接触约束方法并验证，在验证后对地震激励下的结构抬腿和脱轨进行了分析，发现海侧门腿与陆侧门腿相比更难以发生抬腿现象。对结构中不同位置的位移结果进行比较，发现大梁上的位置在水平方向上的位移差距不大，而垂直方向上的位移差距较明显。本研究在分析的过程中未考虑塑性变形带来的影响，对于结构的约束方法尚有可继续探索的空间。