列车行驶对铁路跨越安全防护架的影响分析*

张 杰 吴 晓,2 曹 丹 胡 林 王 威

1西南交通大学机械工程学院 成都 610031 2轨道交通运维技术与装备四川省重点实验室 成都 610031

0 引言

铁路高速列车在轨道上行驶时，空气的黏性作用会带动周围空气一起运动，形成列车风[1]。列车风会对列车周围的物体产生复杂的作用力，当列车速度较高、距离较近时，产生的作用力强度越明显。铁路跨越安全防护架是一种在铁路施工过程中防止电缆坠落或其他高空坠物对铁路造成影响或破坏的装置[2]，其结构如图1所示。防护架在防护作业期间，列车以不同速度通过时会对安全防护架结构产生作用力，该作用力主要与列车速度、列车与防护架距离有关。因此，从评估和完善结构设计的角度出发，有必要对铁路跨越安全防护架的列车风致影响进行研究。

图1 铁路跨越安全防护架

目前，国内外针对列车风致影响已有研究。金海等[3]研究了地铁列车过站时风致环境影响，对监测点进行定量评估，划定站台区域人员的活动区域和舒适范围；张贺等[4]运用SAP2000仿真软件对高速列车过站不同类型单柱雨棚进行研究设计分析，探究现浇组合屋面和采用预制混凝土屋面的单柱站台雨棚的用钢量变化规律以及振型特征，其结果建议在一些地震频发地区使用需采取一定的抗震措施；杨娜等[5]、许伟等[6]研究了高速列车过雨棚时的列车风致效应，用Fluent滑移网格技术结合标准方程湍流模型等数值模拟分析雨棚表面风压分布规律、雨棚开口宽度等参数对其表面风压影响；孙晓亮[7]、王志飞[8]研究了列车高速过站对站台门结构特性的影响，验证了建立仿真模型加载方法的可靠性；杜云超[9]提出了适用于高速列车通过隧道关键空气动力学系数的可压缩流动模型确定方法，研究3种不同类型的高速列车车型以及过隧道时列车表面摩擦系数等参数及适用范围，并将理论计算和仿真试验数据进行对比验证；王英学等[10]采用动网格技术研究隧道中部存在车站时列车会车工况分析，其仿真数据反映了隧道内压缩波和膨胀波产生、传播规律；王飞龙[11]通过建立CRH380A高速列车过隧道的空气动力学模型，采用有限体积法及滑移网格技术对其模型模拟和对初始压缩波等参数进行研究分析；Lim K M等[12]用计算流体力学研究了高速列车通过地铁站时对结构和站台乘客的空气动力学影响，基于仿真结果对高铁对地下车站的不定速流场进行了分析，并对PSD的压力和站台压力变化进行了定量评估；Guo D L等[13]采用动态网格技术研究了列车经过隧道和隧道内相互通过的列车风的特性，选用了4组不同研究速度工况，验证了2个场景的列车运行速度与列车风速之间存在的线性关系；Iliadis P等[14]分析了货运列车通过隧道时的流动进行数值模拟，研究发现列车车头周围的分离流与能量损失、横向振动、噪声和流线偏差有关，且会影响列车周围的速度大小。

综上所述，大多数研究者研究的是列车过雨棚、过站台、过隧道的空气动力学，对于列车过铁路跨越安全防护装备的研究可借鉴列车过雨棚、过站台等的研究，采用数值模拟分析列车过跨越防护架的风压影响，验证跨越防护架结构设计的安全性及稳定性。

1 流体数值仿真理论分析

结合列车运行对防护架结构的实际影响情况，采用标准k-ε湍流模型进行模拟分析,分别给出湍流粘性、湍流雷诺数、湍流动能、能量耗散等模型。

1）湍流粘性

湍流粘性可定义为

式中：ρ为空气密度，k2为湍流速度尺度，cμ为湍流常数，fμ为衰减函数，ε为湍流耗散率。

2）湍流雷诺数

湍流雷诺数方程为

3）湍流动能

湍流动能方程为

4）能量耗散

能力耗散方程为

在上式中，等号右端项分别为生成项、耗散项和壁面项，常数的定义分别为cμ＝ 0.09，cε1＝ 1.45，cε2＝1.92，σk＝ 1.0，σε＝ 1.3。

在上述方程中，近壁衰减函数、壁面项具体计算方式分别为

式中：uS为平行于壁面的流动速度，积分到壁面无滑移边界条件为k＝0，ε＝0。

2 仿真模型的建立

2.1 系统模型建立

构建跨越防护架及列车仿真模型，以标准双线铁路为参照，使用三维软件Solidworks建立装备与列车的仿真模型。将铁路道床视为光滑平面，轨道两侧架设新型铁路跨越安全防护装备。跨越防护架搭建好的尺寸是沿轨道方向为15 m，垂直轨道方向为18 m，在轨道上搭建的高度为15 m。列车车头属于扁平头形状，列车横截面高度为3.4 m，宽度3.3 m，总长度为74 m。车体表面光滑处理，均不考虑转向架、车门等细小部件的影响。

列车距防护架30 m处出发，以不同速度通过跨越防护架区域，出口区域长度设置为106 m，如图2所示。

图2 列车运行距离示意图

列车过跨越防护架所在的外流场区域，流场区为长方体结构，计算区域的总长度为250 m，宽度为50 m，高度为40 m，通过设定外流场的边界条件研究列车通过跨越防护架的影响。

2.2 列车与装置网格划分

列车对防护架的影响是连续的，列车相对防护架处于运动状态。在计算区域内的网格划分中，列车模型与防护架模型区域内的网格划分是整个流场网格划分的关键，使用ICEM-CFD对防护架及列车进行四面体非结构化网格划分，按照网格质量0～1区间，模型中网格质量均大于0.75，最终确定列车的网格尺寸为300 mm。列车过跨越防护架仿真采用动网格技术，仿真区域中存在的边界随时间运动的情况，该区域不存在相对运动。当使用动网格在Fluent中仿真列车运动时，需要定义初始网格、边界运动的方式并指定参与运动的区域，用Profile文件或UDF函数驱动边界运动，流场整体网格模型如图3所示。

图3 流场整体网格分布

2.3 边界条件及计算方法设定

采用动网格技术中的Layering方法仿真列车过跨越防护架，列车、跨越防护架和地面均采用壁面边界条件，该边界条件可以限制流体在流场中的流动。在模型计算时，壁面条件设置为无滑移壁面。

模拟列车过跨越防护架下端在明线上运行，数值仿真列车过跨越防护架，采用Fluent求解非定常不可压缩流动方程和标准k-ε模型，其外流场边界采用压力远场，流体假设为理想气体。设置列车所在运动区域的移动速度，采用有限元体积法离散方程对流体项采用一阶迎风格式离散，扩散项是采用中心差分格式离散，压力速度耦合采用Coupled算法。

设置列车行驶速度分别为160 km/h、250 km/h、350 km/h，拟用时间步长为0.02 s，基于不同列车速度选择相应迭代的总步数，每个时间步的迭代次数为20次，欠松弛因子设为默认值，仿真列车从跨越架一端通过跨越防护架的过程。

3 列车过跨越防护架表面风压分布

跨越防护架会因列车行驶速度的不同，受到不同列车风压的影响，在安全防护架结构的不同位置产生不同的风致响应。单向列车分别以160 km/h、250 km/h、350 km/h的速度通过铁路跨越安全防护架，直至列车驶离防护架区域后停止，分别监测安全防护架进出口共14个位置点表面风压随时间变化的情况，监测点分布如4所示。

图4 跨越防护架监测点分布

3.1 列车行驶速度与安全防护架表面风压的关系

列车以不同速度通过安全防护架入口处表面承受风压随时间变化的监测曲线，如图5所示。由图中曲线可知，装置表面受风压情况随列车运行速度的增加而增大，风压增加时间随列车速度增大而减小。

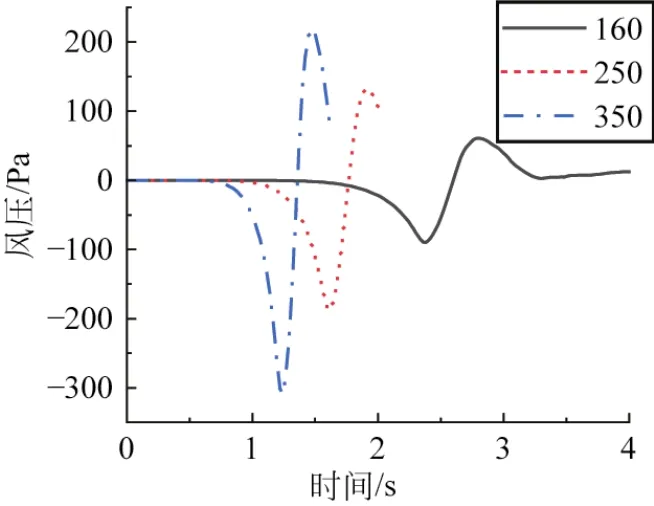
图5 列车不同速度过防护架入口面风压变化情况

3.2 防护架监测点的风压变化

为研究安全防护架结构表面所受风压值与列车行驶速度的关系，可以监测防护架表面上不同位置的风压值随时间的变化情况，不同位置、不同速度数值模拟风压时程对比结果如图6所示。由图6仿真数据可知，列车以160 km/h、250 km/h、350 km/h的速度通过防护架各监测点表面的风压影响趋势一致，分别在接近1 s、0.5 s、0.4 s处产生负风压，产生的最大风压值分别为101.73 Pa、213.96 Pa、351.84 Pa。结果显示，防护架距离列车近端监测点表面风压大于距离列车远端监测点表面风压。

图6 列车不同速度过防护架各监测点风压变化

3.3 防护架高度方向风压分布

由列车不同速度监测点的风压值分析数据可知，速度为350 km/h时的风压值对安全防护架的影响最大，各支腿不同监测点最大正负风压值如表1所示。

表1 车速350 km/h时各监测点最大正负压值 Pa

由图4可知，监测点4、监测点3、监测点2位于支腿1，监测点5、监测点6、监测点7位于支腿2，监测点11、监测点10、监测点9位于支腿3，监测点12、监测点13、监测点14位于支腿4。由表1数据可知，支腿上监测点的高度越高所受正负风压值越小，其中监测点5正负风压值都为最大值，符合列车距离监测点5距离最近的实际情况。

4 列车速度对防护架结构影响

列车车速分别为160 km/h、250 km/h、350 km/h时对安全防护架结构的影响可从监测其结构变形反映，其结构变形数据如图7、图8所示。

图7 未拉缆绳跨越防护架结构的变形随时间变化

图8 拉缆绳跨越防护架结构的变形随时间变化

由图7可知，不同车速通过未作加固处理的跨越防护架所产生的风压对其结构产生的变形较大，车速350 km/h时防护架变形最大，在1.5 s时产生最大变形为1 236.9 mm，大于设计规范规定的材料变化允许值。通过对跨越防护架的4个支腿上方拉缆风绳进行加固，加固后的跨越防护架在车速350 km/h时的变形最大，在1.5 s时产生最大变形为28.55 mm，变形合理且在标准内，结果如图8所示。

跨越防护架在列车不同速度的影响下，结构变形随速度的增加逐渐明显，未拉缆风绳变形比拉缆风绳的结构变形大，可以看出缆风绳对跨越防护架的结构稳定性影响是非常重要。

5 结论

本文针对铁路安全防护架这一铁路邻近装置，数值模拟列车过跨越防护架，采用Fluent求解非定常不可压缩流动方程和标准k-ε方程模型，分析列车以不同速度通过跨越防护架不同位置风压随时间变化情况，监测防护架表面的风压随时间变化规律，主要结论如下：

1）列车不同速度通过安全防护架时，列车车体与跨越架之间的空气会随着列车一起运动，列车的速度越快，安全防护架结构受列车风作用时间越短，其表面瞬态压力变化频率越大。

2）列车以同一速度进入，监测点距离列车越近，其表面风压值越大；列车以不同速度进入，列车速度越快，监测点表面风压值越大。

3）列车以速度350 km/h通过防护架，分析不同高度监测点风压影响数据可知距离列车较近的安全防护架支腿受风压较大，距离列车高度越近，风压值越大。

4）不同车速通过未作加固处理的跨越防护架，所产生的风压对其结构产生的变形较大，大于设计规范规定的材料变化的允许值。通过对跨越防护架的4个支腿上方拉缆风绳进行加固，加固后防护架的最大位移变形为29 mm，符合设计要求。