Adaptive Neural Control for Nonlinear MIMO Function Constraint Systems

Tianqi Yu, Yan-Jun Liu,, and Lei Liu,

Dear Editor,

In this letter, a novel adaptive control design problem for uncertain nonlinear multi-input-multi-output (MIMO) systems with time-varying full state constraints is proposed, where the considered systems consist of various subsystems, and the states of each subsystem are interconnected tightly.It is universally acknowledged that in the existing researches with state constraints, system constraint bounds are always constants or time-varying functions.Different from previous methods, the constraint boundary of this letter is regarded as a special function of not only time but of state variables.In order to handle time-varying full state constraints, the tangent type time-varying barrier Lyapunov functions (tan-TVBLFs) are introduced.By combining neural networks (NNs) and backstepping technique, an intelligent controller is developed.Meanwhile, we introduce an even function to guarantee the feasibility of NN approximation of unknown functions over practical compact sets.The feasibility of the mentioned control strategy is certified through the simulation results.

Over recent decades, the control strategy of nonlinear systems has drawn lots of attention due to classical control methods are not sufficient for nonlinear characteristic problems.Thus, various advanced control techniques for uncertain nonlinear systems are proposed in[1] and [2].Subsequently, NNs and fuzzy logic systems (FLSs) have been widely used [3].Via fast finite-time stable theory and FLSs, a fuzzy dynamic surface control with uncertainties is studied in [4],where the computational complexity is reduced.An adaptive backstepping output feedback control strategy is investigated by taking unmeasured states into consideration [5].Further, an adaptive faulttolerant controller is constructed in [6], and a control scheme of pure feedback systems is proposed by [7].Nevertheless, the impact of output and state constraints has been neglected according to above descriptions.

It is unavoidable to exist various constraints in practical systems,which restricts the system performance and stability.Consequently, a large number of control schemes have been put forward to settle constraints including state feedback control [8], and output feedback control [9].For further research, barrier Lyapunov function (BLF)regarded as an available approach to solve constraints has been considered by [10].An output feedback control of full state constrains is presented by utilizing Integral barrier Lyapunov functionals (IBLF)[11].Surprisingly, this approach overcomes the limitation of conservatism comparing with traditional BLFs.A full state-constrained control design for uncertain stochastic nonlinear systems is developed by [12] via using time-varying BLFs.But, the mentioned approaches are confined to satisfy single-input single-output (SISO)nonlinear systems.

More complex, the constraint system mentioned above is developed to MIMO uncertain system or large-scale systems, which is a challenging task to devise an appropriate control strategy.In [13], a dynamic surface control strategy based backstepping algorithm is introduced.Furthermore, the tracking control approaches of input saturation has been investigated by [14].An NN adaptive control scheme considering full state constraints in block-triangular form is addressed via utilizing the backstepping-based IBLF in [15].With the help of backstepping algorithm, an adaptive control design of output-constrained large-scale systems is presented by [16].However,all the existing constraint boundaries of time-varying constraint researches are only relevant to time without considering state.

Inspired by above descriptions, this letter develops an adaptive NN control method for uncertain nonlinear MIMO systems with unknown smooth functions and time-varying full state constraints.The main contributions are listed as follows.

1) In existing BLF based state constraints, the constraint bounds are regarded as constant [12] or time-varying functions [14].Different from previous boundary that only changes with time, the state constraint boundary of this letter is regarded as a particular function of not only time but of state variables, which is seldom developed in previous results.

2) To guarantee the feasibility of NN approximation of unknown functions, a novel control method is proposed over practical compact sets and a suitable controller is successfully constructed.

3) The full state constraints are taken into consideration in nonlinear MIMO systems by utilizing tan-TVBLFs.The aim of using tan-TVBLFs is to ensure all states remain within the time-varying constraint range.Meanwhile, the considered systems consist of subsystems, and the states of each subsystem are interconnected.

According to the above figures, it is obvious that the time-varying state constraints are not broken.The system inputs and the adaptive laws are shown in Fig.3.It can be seen that they all maintain a relatively stable and bounded state in a small neighborhood.Apparently,these trajectories tend to stabilize.

Conclusions: The novel adaptive NN control problem based on tan-TVBLFs is proposed for uncertain nonlinear MIMO systems with both time-varying full state constraints and unknown function.The constraint boundary in this letter is a particular function of not only time but of states.And tan-TVBLFs are constructed to keep the states from violating time-varying constraint boundary.Ultimately, simulation example certifies the feasibility of presented control approach.In the future, an observer-based adaptive NN control for a class of nonlinear MIMO systems will be developed.Furthermore, we will apply the complex time-varying constraints in this letter to chemical production, unmanned driving and other practical systems.

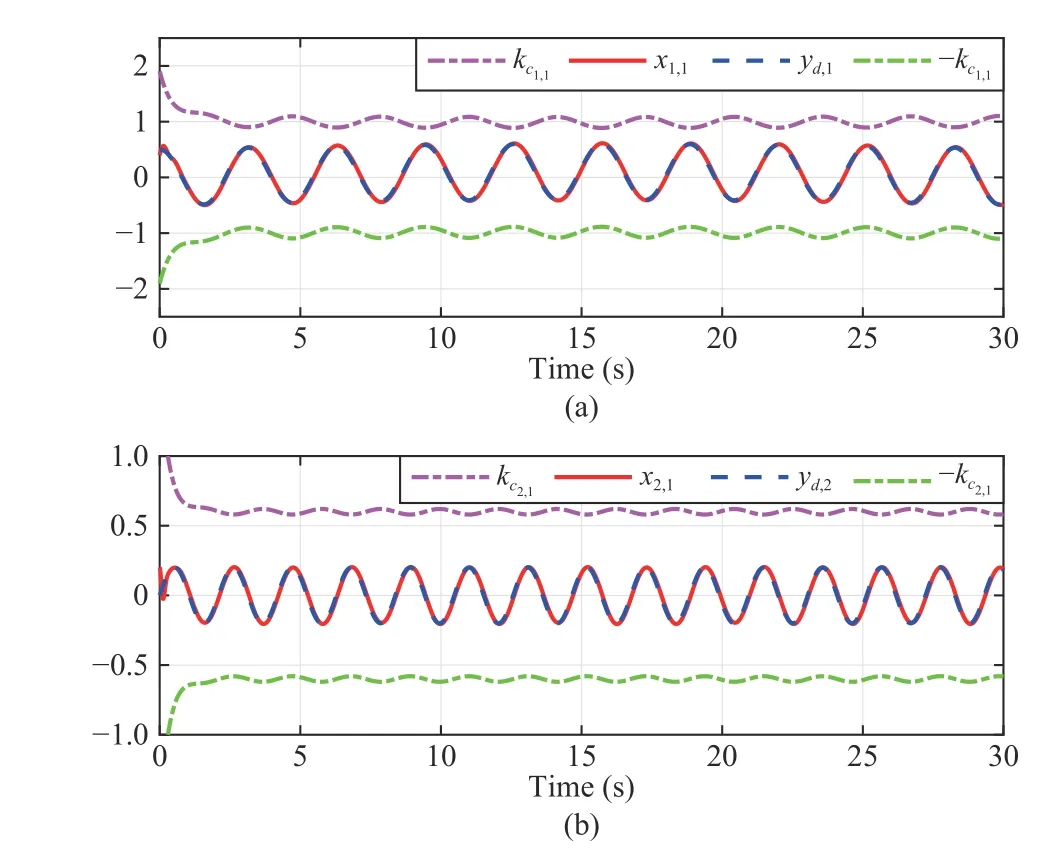
Fig.1.Trajectories of desired signal and system output: (a) yd,1andx1,1;(b) yd,2and x2,1.

Fig.2.Trajectories of states: (a) x1,2and (b) x2,2.

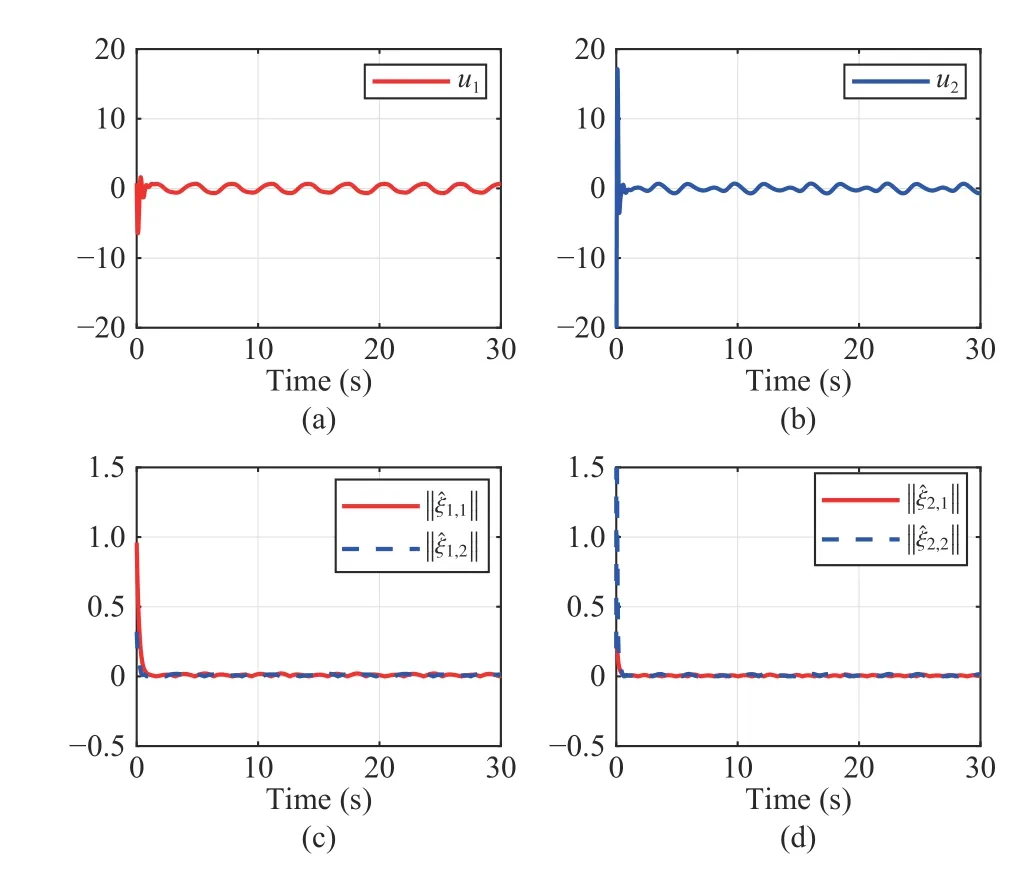
Fig.3.Trajectories of actual controller and adaptive laws: (a) u1; (b) u2; (c)and ; (d)and

Acknowledgments:This work was supported in part by the National Natural Science Foundation of China (62025303,62173173).