Group Hybrid Coordination Control of Multi-Agent Systems With Time-Delays and Additive Noises

Chuanjian Li and Xiaofeng Zong,

Abstract—A new kind of group coordination control problemgroup hybrid coordination control is investigated in this paper.The group hybrid coordination control means that in a whole multi-agent system (MAS) that consists of two subgroups with communications between them, agents in the two subgroups achieve consensus and containment, respectively.For MASs with both time-delays and additive noises, two group control protocols are proposed to solve this problem for the containment-oriented case and consensus-oriented case, respectively.By developing a new analysis idea, some sufficient conditions and necessary conditions related to the communication intensity between the two subgroups are obtained for the following two types of group hybrid coordination behavior: 1) Agents in one subgroup and in another subgroup achieve weak consensus and containment, respectively;2) Agents in one subgroup and in another subgroup achieve strong consensus and containment, respectively.It is revealed that the decay of the communication impact between the two subgroups is necessary for the consensus-oriented case.Finally, the validity of the group control results is verified by several simulation examples.

I.INTRODUCTION

COORDINATION control of multi-agent systems (MASs)has become an important theme in the control community, including consensus control, containment control and so on.For these problems, fruitful achievements have been obtained.Under time-delays, many consensus results have been obtained [1]–[4].In general, time-delays have negative impact on consensus, but Yuet al.[4] revealed that appropriate time-delays can play a positive role in delay-induced consensus problems.The effects of additive and multiplicative measurement noises on consensus behaviors were revealed in[5]–[8], [9] and [10], respectively.The consensus problems were studied for MASs with both time-delays and additive noises in [11]–[14].

As a kind of coordination control problem, the containment problem has also received extensive attention.Under a relatively ideal environment, many interesting results about containment problems have been obtained, as shown in [15]–[18].When time-delays exist in MASs, the research results for the containment problem can be seen in [19]–[21].The effects of additive noises on containment behaviors were revealed in[22] and the containment control of MASs with both timedelays and additive noises was studied in [23].

It can be seen that the above studies all focused on the problem where agents in a whole system achieve global coordination behavior.However, in some practical application scenarios where multiple tasks such as tracking and striking need to be performed simultaneously, global coordination control may not be able to accomplish these tasks.Hence, it is necessary to investigate group coordination control problems such as group consensus and group containment problems.These require agents in different subgroups to achieve different coordination states.In fact, many scholars have made efforts for solving group coordination control problems.Yu and Wang [24]and [25] studied group consensus under the assumption that the effect between the two subgroups is balanced.Then, the assumption was relaxed in [26] and [27], where the group consensus of MASs with generally connected topology were investigated.Some interesting results about group consensus under measurement noises can be seen in [28] and [29].The results about the bipartite consensus problem can be found in[30]–[32].

Note that the aforementioned works about group coordination control all focused on the problem that all subgroups achieve consensus behavior.However, agents in different subgroups may be required to achieve different coordination behaviors for some multi-objective tasks such as military tasks[33].Moreover, for opinion dynamics in social networks,there may appear agreement or fluctuation which need to be characterized by different coordination behaviors in a whole organization [34].Hence, it is natural to think about the conditions that consensus can be achieved for one subgroup and containment be achieved for another subgroup in a whole MAS.This problem is called group hybrid coordination control problem, which has not been addressed, even in an ideal environment.

In this paper, we study the group hybrid coordination control problem of MASs with both time-delays and additive noises.We consider a whole MAS that consists of two subgroups, where communications between the two subgroups are unidirectional and only one subgroup can receive information from another subgroup.The case where a subgroup receiving information from another subgroup is required to achieve containment is called the containment-oriented case.Similarly, the case where the subgroup receiving information from another subgroup is required to achieve consensus is called the consensus-oriented case.Since there are communications between the two subgroups and different subgroups are required to achieve different coordination behaviors for a whole MAS, the system dynamics cannot simply be analyzed as a whole.This makes the existing control protocols, methods and conditions, such as those in [14], [22], and [24]–[32],fail to solve the group hybrid coordination control problem.Then, in this paper, our goal is to explore appropriate analysis methods and obtain some conditions for solving the new kind of group coordination control problem, i.e., the group hybrid coordination control problem of MASs with time-delays and additive noises.

The main contribution of this paper can be concluded as follows.

1) A new kind of group coordination control problem-group hybrid coordination control is investigated and two new group control protocols are designed to solve this problem.By developing a new analysis idea, some sufficient conditions and necessary conditions are obtained for the group hybrid coordination control problem under time-delays and additive noises.It is found that the conditions for the containment-oriented case are weaker than those for the consensus-oriented case.And for the consensus-oriented case, the conditions for weak consensus are weaker than those for strong consensus.

2) The influence mechanism of the communication impact between the two subgroups on group hybrid coordination control problem of MASs with both time-delays and additive noises is revealed: the decay of the communication impact between the two subgroups is necessary for the consensus-oriented case.This provides hints in the design of control gain functions for the similar group coordination control problem.

The structure of this paper is organized like this: In Section II,the system model, some basic concepts, and lemmas are introduced.Sections III and IV investigate the containment-oriented case and the consensus-oriented case, respectively.Some simulation results are given in Section V.Section VI summarizes this work and gives some other interesting questions for future research.

Notations:The following notations are used in the process of analysis.1nand ϑn,iare twon-dimensional column vectors,where each element is one for 1n, and theith element is one and others are zero for ϑn,i.Them-dimensional identity matrix is denoted byIm.Fora,b∈R,a∧b= min{a,b}.For any complex numberλin complex space C, its real part is denoted byRe(λ).For the matrix or vectorP, its transpose and Euclidean norm are denoted byPTand ‖P‖, respectively.For a given random variable or vectorX, its mathematical expectation is denoted by EX.

II.PRELIMINARIES

Let G=(V,E,A) be a weighted directed graph, where V={1,...,i,...,n}is the set of nodes withirepresenting theith agent, E ⊆V×V denotes the set of edges and (i,j)∈E is a edge of G.A=[aij]∈Rn×nis the weighted adjacency matrix with real adjacency weighting elementsaij=1 or0 indicating whether or not there is an information flow from agentjto agentidirectly.Moreover, we assumeaii=0 for alli∈V.The set of neighbors of nodeiis denoted byNi, that is,aij=1 forj∈Ni.The Laplacian matrix of G is denoted by L.A directed path is a sequence of edges with the form(i−1,i), (i,i+1),....A directed graph contains a directed spanning tree if there exists at least one node that has a directed path to all other nodes.In the directed graph G, the node which has no parent node is called a root.A digraphG has a spanning forest if there exists a directed forest which is the spanning subgraph of G.More details about the spanning subgraph, directed forest and spanning forest can be found in[22].

In this paper,n+m(n≥1,m＆gt;2) first-order continuous-time agents compose a MAS with a directed communication graph G=(V,E,A).We divide G=(V,E,A) into two subgraphs G1=(V1,E1,A1) and G2=(V2,E2,A2), whereV1={1,...,n}, V2={n+1,...,n+m} and E1=V1×V1, E2=V2×V2,that is, the firstnagents belong to one subgroup, which is denoted by Ψ1, and the lastmagents belong to another subgroup, which is denoted by Ψ2.Moreover, letNi=N1i∪N2i,whereN1i⊆V1andN2i⊆V2are the sets of neighbors belonging to Ψ1and Ψ2of theith agent respectively.Here,each agent has the following dynamics:

Assumption 1:G1contains a spanning tree and G2has a spanning forest whose roots are exactly the leaders in MASs.Moreover, the communications between the two subgroups are unidirectional and only one subgroup can receive information from another subgroup.

In the communication environment considered in this paper,the exchange of state information between agents can not be performed accurately.It is often assumed that the agentican receive information from its neighbors as follows:

whereyji(t) denotes the measured value of thejth agent’s state by theith agent, τ ≥0 is the time-delay, ηji(t)∈R denotes the measurement noise and σjiis the corresponding intensity function.Here, let the initial states be constants,X1(t)=∆1∈tainment-oriented case and consensus-oriented case respectively, we will obtain some useful results and find some interesting phenomena for group hybrid coordination behaviors under time-delays and additive noises.

III.THE CONTAINMENT-ORIENTED CASE

Remark 3:Note that there are communications between the two subgroups.This means that the MAS is still a whole system.Under the assumption that the in-degrees from the other subgroups are equal at any time for each node in one subgroup, Shang [28] concluded that the group consensus behavior can be reached under appropriate time-delay and multiplicative noise intensity.Under time-delays and additive noises, we determine to study the group hybrid coordination control problem when the assumption mentioned above is released.This is a key problem that will be explored in this paper.

Based on interactions between any two agents in the environment with both time-delays and additive noises, we propose the control protocol as follows:

B.Stochastic Strong Consensus +Stochastic Containment

Above, we explored the group hybrid coordination control problem for the containment-oriented case and obtained some interesting results.Then, for the consensus-oriented case, we need to determine if the above conditions sufficient.We will explore this problem in Section IV.

IV.THE CONSENSUS-ORIENTED CASE

B.Stochastic Strong Consensus +Stochastic Containment

Remark 8:From the above analyses, we can see that more conditions are needed to achieve group hybrid coordination control compared to global coordination control.Since different subgroups are required to achieve different coordination behaviors, the system dynamics cannot simply be analyzed as a whole.This results in the existing methods and conditions,such as those in [14], [22], and [24]–[32], unable to solve the group hybrid coordination control problem.Hence, in this paper, we develop a new analysis idea to study this problem.Then, some sufficient conditions and necessary conditions are obtained, and the influence mechanism of the communication impact between the two subgroups is revealed for the group hybrid coordination control problem of MASs with both timedelays and additive noises.

V.SIMULATION

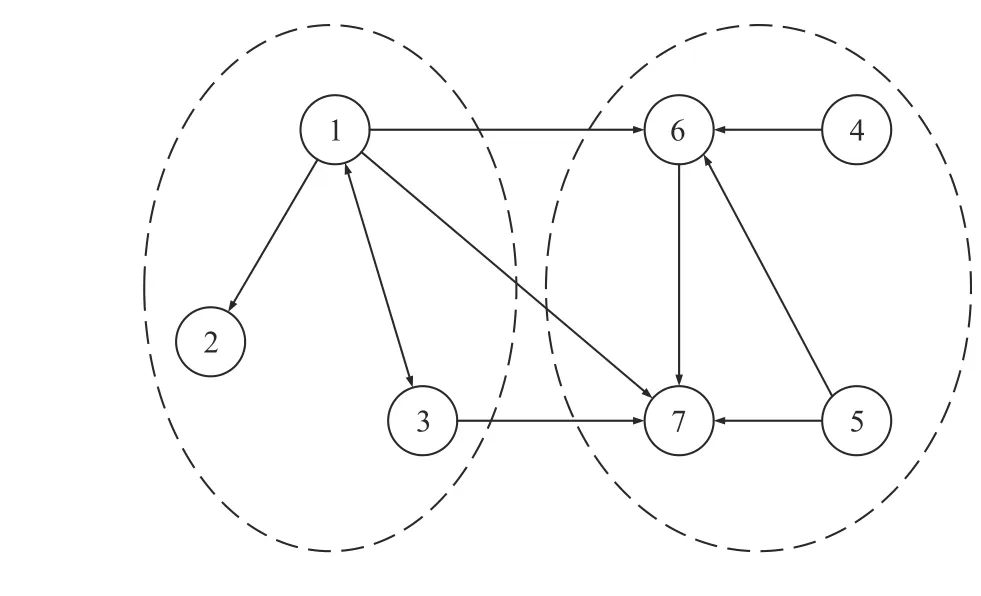
Fig.1.The communication graph: The containment-oriented case.

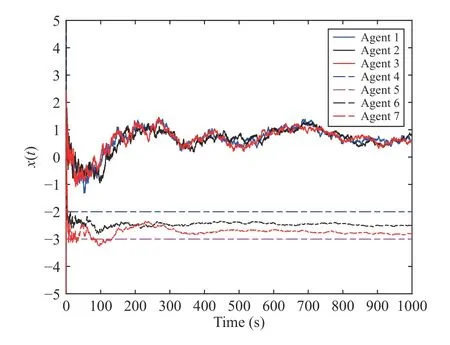
Fig.2.The containment-oriented case: Stochastic weak consensus + Stochastic containment.

Now, we give a counter-example to show the necessity of the decay of the communication impact between the two subgroups for the consensus-oriented case.We considerτ=0.5,c1(t)=0.8(1+t)−0.9,c2(t)=0.9(1+t)−1and κ(t)=1.Other conditions are the same as above.It is easy to get that Assumption 6, conditions (C1)−(C6), (C8) and (C10) hold but(C9) does not hold.Then, we obtain Fig.7, which shows that the given MAS fails to achieve group hybrid coordination behavior.

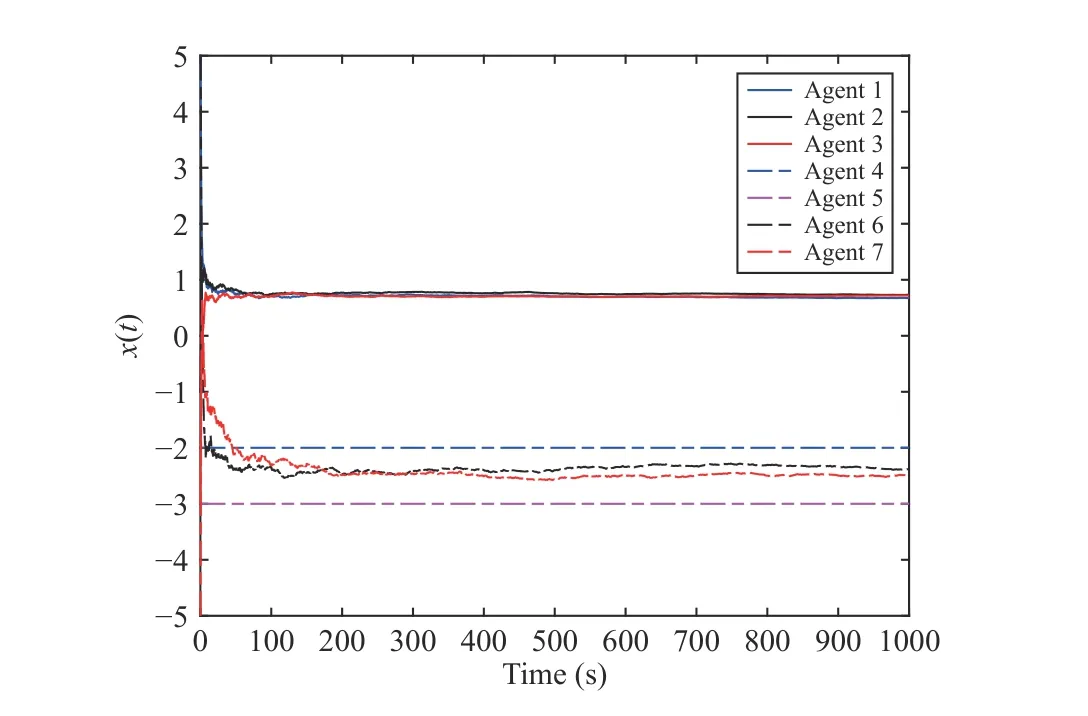
Fig.3.The containment-oriented case: Stochastic strong consensus + Stochastic containment.

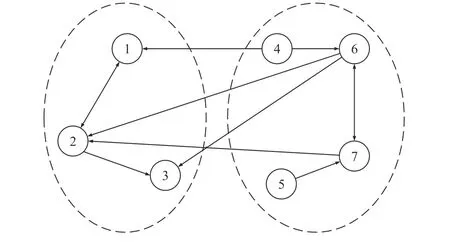
Fig.4.The communication graph: The consensus-oriented case.

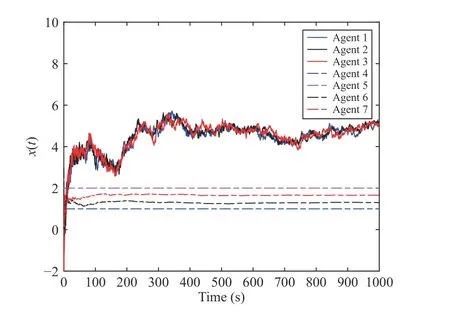
Fig.5.The consensus-oriented case: Stochastic weak consensus + Stochastic containment.

VI.CONCLUSIONS

Fig.6.The consensus-oriented case: Stochastic strong consensus + Stochastic containment.

Fig.7.A counter-example for the consensus-oriented case.

This work addressed the group hybrid coordination control problem of MASs with both time-delays and additive noises.The containment-oriented case and the consensus-oriented case were discussed respectively.Using the semi-decoupled skill and some estimation methods, this work provided a new analysis idea to investigate the group hybrid coordination control problem.Then, some sufficient conditions and necessary conditions were obtained and some interesting phenomenons were found.It is concluded that to solve the group hybrid coordination control problem, more conditions are needed than to solve the global coordination control, and the decaying condition of communication impact between the two subgroups is necessary for the consensus-oriented case.Intuitively, in real networks, the communication impact between the two subgroups may gradually weaken with the increase of the distance between agents in different subgroups.This might be beneficial for designing the group control protocol.Furthermore, the following new findings are obtained: 1) The conditions for the containment-oriented case are weaker than for the consensus-oriented case; 2) For the consensus-oriented case, the conditions for weak consensus are weaker than those for strong consensus.

Recently, many important results on distributed coordination control have been obtained, such as coordination control based on dynamic event-triggered [36] and [37].Determining how to apply these advanced control strategies to the control problem studied in this paper to improve the system communication efficiency and execution capability is a future direction of investigation.