Cooperative Target Tracking of Multiple Autonomous Surface Vehicles Under Switching Interaction Topologies

Lang Ma, Yu-Long Wang,, and Qing-Long Han,

Abstract—This paper is concerned with the cooperative target tracking of multiple autonomous surface vehicles (ASVs) under switching interaction topologies.For the target to be tracked, only its position can be measured/received by some of the ASVs, and its velocity is unavailable to all the ASVs.A distributed extended state observer taking into consideration switching topologies is designed to integrally estimate unknown target dynamics and neighboring ASVs’dynamics.Accordingly, a novel kinematic controller is designed, which takes full advantage of known information and avoids the approximation of some virtual control vectors.Moreover, a disturbance observer is presented to estimate unknown time-varying environmental disturbance.Furthermore,a distributed dynamic controller is designed to regulate the involved ASVs to cooperatively track the target.It enables each ASV to adjust its forces and moments according to the received information from its neighbors.The effectiveness of the derived results is demonstrated through cooperative target tracking performance analysis for a tracking system composed of five interacting ASVs.

I.INTRODUCTION

MOTION control of autonomous surface vehicles (ASVs)has garnered widespread attention due to its extensive marine applications in military reconnaissance, environmental monitoring, ocean exploration, transportation, offshore inspections, etc.[1]–[3].Several interesting results about some typical motion control issues are reported in the literature, including heading control [4] and [5], dynamic positioning [6]–[9], target tracking [10]–[12], trajectory tracking [13]and [14], and path following [15]–[17].In particular, maritime target tracking, whose purpose is to drive corresponding marine vehicles to track a moving target, has received much attention [18].Generally, the only available target information is the instantaneous position and velocity [10].In the past two decades, some interesting control methods about maritime target tracking have been presented [10], [11] and[19]–[21].For example, a straight-line target tracking scenario is designed to track a high-speed target moving in a straight line [10].For an unmanned surface vehicle with unknown dynamics and bounded torques, a bounded neural network control scheme is given to track a target by using line-of-sight range and angle measurements [11].For an autonomous underwater vehicle, a prescribed performance bound method is presented to achieve target tracking and guarantee the transient performance [19].For an autonomous robotic vehicle, a switched logic-based control strategy is proposed to address a target tracking problem by utilizing range measurements only [20].Note that the above-referenced results mainly involve one-to-one tracking, i.e., one marine vehicle tracking one target.However, some maritime target tracking missions require the cooperation of a fleet of ASVs,which can improve flexibility, robustness, and efficiency of mission completion.For a group of ASVs, the cooperative target tracking problem is far from being resolved.Therefore,how to achieve cooperative target tracking for multiple ASVs deserves in-depth investigation, which is the first motivation of this paper.

In most cases, it is assumed that both position and velocity information of the maritime target can be either measured or received by follower ASVs [10].For one ASV, however, it is costly and difficult to obtain the accurate velocity of the target [22] and [23].Thus, how to track a target by using only its position information measurement is of paramount importance.On the other hand, in a practical target tracking system composed of multiple ASVs, some of the ASVs cannot obtain the target information due to restrictions of distances and/or external environments.To address this problem, some existing results adopt leader-follower tracking control schemes(see in [10], [11], [22], [24]), which can be sketched as“ASV 1 tracks the target, ASV 2 follows ASV 1, ASV 3 follows ASV 2...”.This means that one ASV only has one neighbor.Specifically, one ASV can only track the target or follow another ASV by measuring/receiving information from it.In this case, if one communication link or one measuring device fails, the cooperative target tracking mission may fail.In the field of multi-agent system control, the distributed control scheme provides a solution to this dilemma [25]–[30].However, how to apply the distributed scheme to the cooperative target tracking is still challenging, not to mention in the case of lacking the target’s velocity information.This is the second motivation of this paper.

The interaction between the target and the ASVs can be described by a communication network.In some existing results concerning cooperative control of multiple ASVs,interaction network topologies are assumed to be fixed[31]–[33].In practical maritime tracking applications, the connectivity of the corresponding interaction topology may switch due to link failures, sensor incapabilities, channel attenuation, alteration of missions, and disturbance of complex environments.This heightens the need for investigating the cooperative control problem of multiple ASVs under switching topologies.Actually, under switching topologies,the cooperative control of multi-agent systems has been studied in the existing literature [34]–[37].However, these results cannot be directly extended to the cooperative control of multiple ASVs.For a tracking system composed of multiple ASVs, the cooperative target tracking problem under switching topologies has not been adequately addressed hitherto.This is the third motivation of this paper.

Based on the discussions above, this paper focuses on cooperative target tracking controller design for a maritime tracking system composed of multiple ASVs subject to switching interaction topologies.We consider the case that the velocity of the target to be tracked is unavailable to all the ASVs and only the position information of the target can be measured/received by some of the ASVs.This paper first starts with the cooperative target tracking control problem formulation, in which a distributed target tracking error is introduced.Then, in order to integrally estimate unknown target dynamics and neighboring ASVs’dynamics, a distributed extended state observer (DESO) is constructed.Accordingly,a novel kinematic controller is designed.Different from some existing kinematic controllers, it can take full advantage of known information and avoid the approximation of some virtual control vectors.Moreover, a disturbance observer is presented to estimate unknown time-varying environmental disturbance.Furthermore, a distributed dynamic controller is designed to regulate the involved ASVs to achieve cooperative target tracking.The main contributions of this paper are highlighted as follows.

1) For each ASV, a DESO taking into account switching topologies is designed to integrally estimate unknown target dynamics and neighboring ASVs’dynamics.Compared with the extended state observer presented in [11], [16], [38], [39],the DESO in this paper is in a distributed manner, which is more suitable for estimating unknown dynamics including not only the target’s but also neighboring ASVs’information;

2) A novel kinematic controller design method is proposed.It contains not only the estimated error term but also the actually known error term.This can make full use of known information.The approximation of some virtual control vectors can also be avoided;

3) A distributed dynamic controller is designed to drive the involved ASVs to cooperatively track the target.It enables each ASV to adjust their forces and moments according to the received information from its neighbors.

Notation:Throughout this paper,Iand 0 represent, respectively, an identity matrix and a zero matrix with appropriate dimensions.Inrepresents ann×nidentity matrix.0nis a column vector with all elements being 0.‖·‖ is the Euclidean norm.⊗ denotes the matrix Kronecker product.For brevity,this paper omits the time argumentt, e.g.,x(t) is denoted asxin this paper.

II.PRELIMINARIES

In this paper, we consider a maritime target tracking system consisting ofNASVs, which aims to cooperatively track a marine target.

This paper considers the case that linear and angular velocities of the target are unknown.Some of theNASVs can obtain the position vector information of the target, which means that the target is a neighbor of them.Treat the target as the node 0.The information exchange between the target and theNASVs can be described by a weighted and augmented graph G (with nodes 0, 1, 2,...,N).The graph G consists of graph G, the node 0, and edges between the target and ASVs whose neighbors contain the target.Denoteai0as the communication weight from the target to the ASVi(pinning weight),whereai0＆gt;0 if the target is a neighbor of the ASVi; otherwise,ai0=0.The pinning matrix isD=diag{a10,a20,...,aN0}.

III.PROBLEM FORMULATION

The kinematical equation of the target is described by

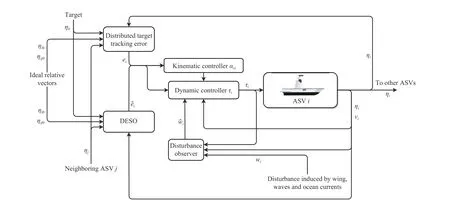
Fig.1.Diagram of the design process.

IV.CONTROLLER DESIGN

In this section, a DESO is first designed to estimate the integrated unknown dynamics of the target and neighboring ASVs.Accordingly, a novel kinematic controller design method is proposed.A disturbance observer is then given to estimate the unknown time-varying disturbance vectorwi.Next, a distributed dynamic controller is derived to regulate theNASVs to cooperatively track the target with kinematical equation (2).The design process is illustrated in Fig.1.

A.Estimation of Unknown Dynamics

B.Kinematic Controller Design

C.Disturbance Observer Design

Consider the following Lyapunov-Krasovskii functional candidate:

D.Distributed Dynamic Controller Design

In this subsection, a distributed dynamic controller is designed according to the DESO (8), the kinematic controller(19), and the disturbance observer (21).

Consider the following Lyapunov-Krasovskii functional candidate:

V.TARGET TRACKING PERFORMANCE ANALYSIS

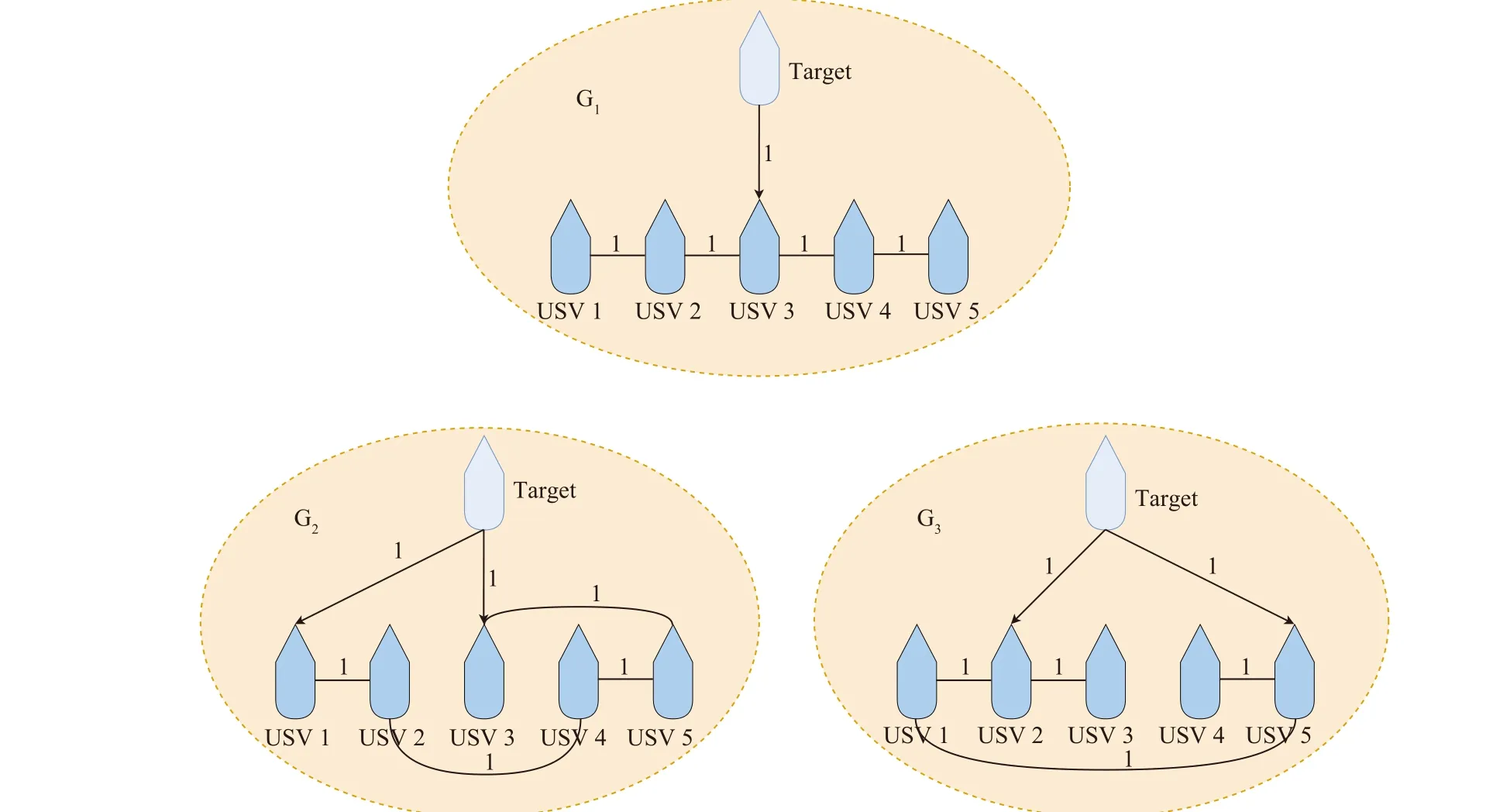
Fig.2.Switching interaction topologies.

Fig.3.Switching signal.

Based on the above-mentioned parameters and initial conditions, trajectories of the target and the five ASVs, distributed errors, and estimation errors of the DESO are illustrated in Figs.4−6, respectively.From Figs.4 and 5, one can see that the five ASVs can cooperatively track the target with desired accuracy under the influence of the switching topologies.Fig.6 shows the estimation errors of the DESO.This demonstrates the validity of the DESO.

Fig.4.Trajectories of the target and the five ASVs, and their snapshots at two time instants.

Then, we consider the case that the ideal relative vector function ηi0(∀i∈V) is time-invariant.

The five time-invariant ideal relative position vectors are described by

Based on the above-mentioned parameters and initial conditions, the corresponding results are shown in Fig.7.From Fig.7, one can conclude that under the influence of switching topologies, the cooperative target tracking is achieved.

Next, comparing Figs.4 and 7, we can observe that the two line formations formed by the five ASVs is in different reference frames.The formation in Fig.4 is in the body-fixed frame of the target, while the formation in Fig.7 is in the earth-fixed frame.This means that we can achieve cooperative target tracking in different reference frames by adjusting the ideal relative vector ηi0(∀i∈V).

VI.PERFORMANCE COMPARISON FOR DIFFERENT CONTROLLER DESIGN SCHEMES

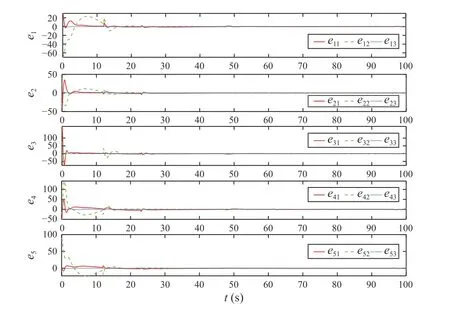
Fig.5.Distributed tracking errors.

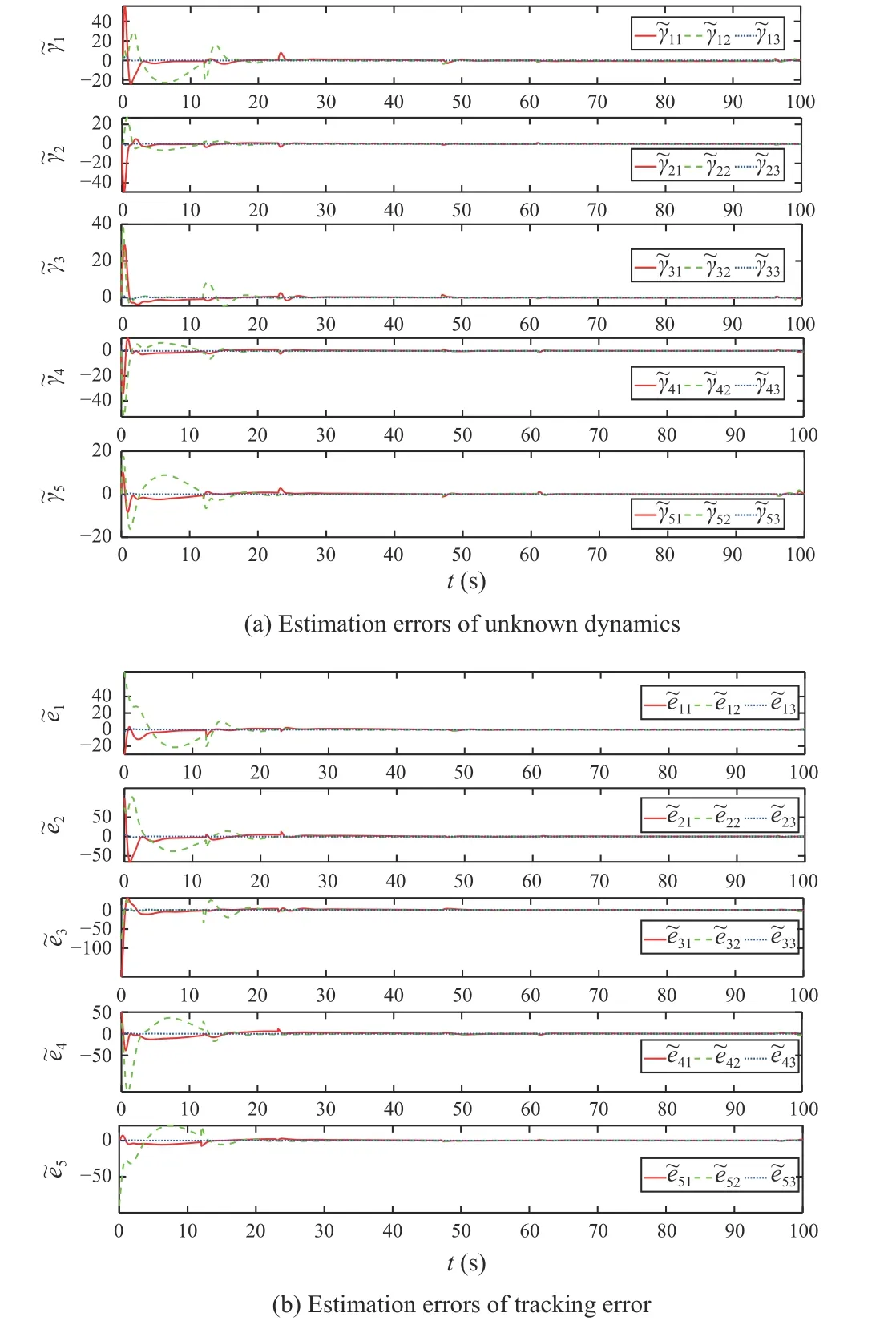
Fig.6.Estimation errors of the DESO.

In this section, we compare the cooperative target tracking performance between the DESO-based tracking controller designed in this paper and the tracking controller designed in[12].We consider a maritime target tracking system with three ASVs.For comparison, the interaction topology is given as a fixed one, which is shown in Fig.8.

Fig.7.Trajectories of the target and the five ASVs, and their snapshots at three time instants.

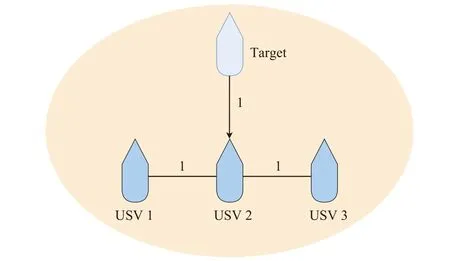
Fig.8.Interaction topology of one target and three ASVs.

The trajectory of the target is the same as the one in Section V.The three time-varying ideal relative position vectors are described by

For the target to be tracked, its velocity is unavailable to all the ASVs, while its position information can only be measured/received by some of the ASVs.In this case, this paper uses coordinate transformation from ηitoeiand estimates the unknown dynamics γithrough a DESO, while in [12], each ASV needs to estimate the target’s position and velocity in the earth-fixed frame by a distributed observer.The difference makes the tracking performance different in this paper and[12].The trajectories of the three ASVs under the tracking controllers in this paper and [12] are presented in Fig.9.From Fig.9, one can see that the control scheme in this paper provides a smaller target tracking error.

Fig.9.Trajectories of the three ASVs under the tracking controllers in this paper and [12].

VII.CONCLUSIONS

The cooperative target tracking has been addressed under switching interaction topologies.A DESO has been designed to integrally estimate unknown target dynamics and neighboring ASVs’dynamics.A novel kinematic controller has been designed, which can make full use of known information and avoid the approximation of some virtual control vectors.A disturbance observer has been presented to estimate unknown time-varying environmental disturbance.A distributed dynamic controller has been designed to regulate theNASVs to cooperatively track the target.Under switching interaction topologies, the effectiveness of the derived results has been demonstrated through cooperative target tracking performance analysis for a maritime target tracking system composed of five interacting ASVs.

Motivated by [46] and [47], our future research will focus on the cooperative target tracking of multiple ASVs under actuator saturation and actuator faults.