刚柔异相水润滑轴承复合材料优化设计研究
2023-03-25李瑞卿刘祺霖李远赜
李瑞卿,金 勇,刘祺霖,李远赜,罗 斌
(1. 武汉理工大学 交通与物流工程学院,湖北 武汉 430063;2. 中国舰船研究设计中心,湖北 武汉 430064)
0 引 言
近年来,仿生材料开始进入人们的视野[1-2],相较于传统材料,仿生复合材料可以通过内部的微结构设计来实现特定的功能或者是提高材料的性能,是目前材料领域研究的一大新热点[3]。水润滑轴承是以自然水为润滑介质的一种轴承,目前水润滑轴承技术已经在许多舰船中得到广泛的应用,尤其在水润滑轴承内衬材料的研究上,是许多精密加工行业的前沿研究课题[4]。但是水润滑轴承也面临了一些问题,橡胶内衬材料应用广泛,但要经过改性处理[5]。轴承衬套沟槽的结构对润滑液的流动有着至关重要的影响等[6-7],这些问题限制了水润滑轴承的发展,利用传统加工方法很难解决这些问题[8-9]。相比于传统的水润滑轴承内衬材料,目前复合仿生材料并没有大面积应用该领域,研究潜力很大。而基于复合仿生材料技术,可以制造出具有纤维结构的复合材料[10-11]。如对橡胶材料进行改性处理,提高它的亲水性和自润滑性能[12-13],从而提高轴承内衬的摩擦磨损性能[14]。利用CFD 软件对模型进行有限元分析[15],利用数字技术对模型结构不断优化,改良内衬材料的结构,设计出最优的布局。之前对于水润滑轴承仿生材料的仿真研究,多关注在摩擦学性能,关于轴承内衬材料的承载能力研究较少,而轴承的承载能力反映了水润滑轴承的力学性能。
本文从板条结构中取出一个微结构体积单元进行分析,体积单元可以代表整体结构的力学性能,通过对体积单元的分析,得出刚性纤维部分的结构参数即纤维直径和纤维螺旋角这2 个参数对于体积单元力学性能的影响。
1 体积单元有限元分析及结构参数优化
生物界的多功能材料往往都是由刚性材料(如生物陶瓷和纤维素)和柔性材料(如蛋白质和木质素)2 种成分以精妙的微结构耦合而成。
如图1 所示,向柔性材料基体(丁腈橡胶、聚氨酯等)加入高强度刚性材料纤维(如碳纤维),可获得优越力学性能的轴承材料。由于在基体内部加入刚性纤维,使得复合材料硬度增加,抗变形能力提高。对于刚柔异相复合材料结构,不同的纤维螺旋角度,不同的纤维半径都有可能对结构的力学性能产生较大的影响。
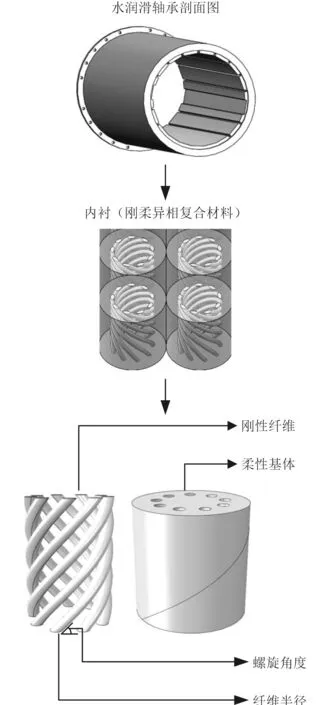
图1 刚柔异相复合材料结构示意图Fig. 1 Schematic diagram of rigid flexible heterogeneous composite structure
本文使用有限元分析软件Abaqus 对微结构模型进行有限元分析,由于水润滑轴承的结构具有对称性,因此采用一个圆柱体积单元,圆柱体的底部圆半径为5 mm,高度为10 mm。为对比纤维结构对材料的影响,分别建立无纤维结构和有纤维复合结构2 种模型进行比较。
1.1 无纤维结构体积单元有限元分析
为分析不同材料无纤维结构体积单元的力学性能,采用4 种水润滑尾轴承常用材料,材料参数如表1 所示。

表1 4 种材料的参数Tab. 1 Parameters of 4 materials
采用单向压缩试验对4 种材料进行仿真分析。由于材料本身的密度对于整个结构的动态响应特性影响并不明显,因此选用静态通用求解器Standard 对模型进行求解。对于模型边界条件设置,向圆柱体积单元上表面施加1 MPa 的表面载荷,设定下表面的边界条件为铰结(pinned)约束(见图2)。
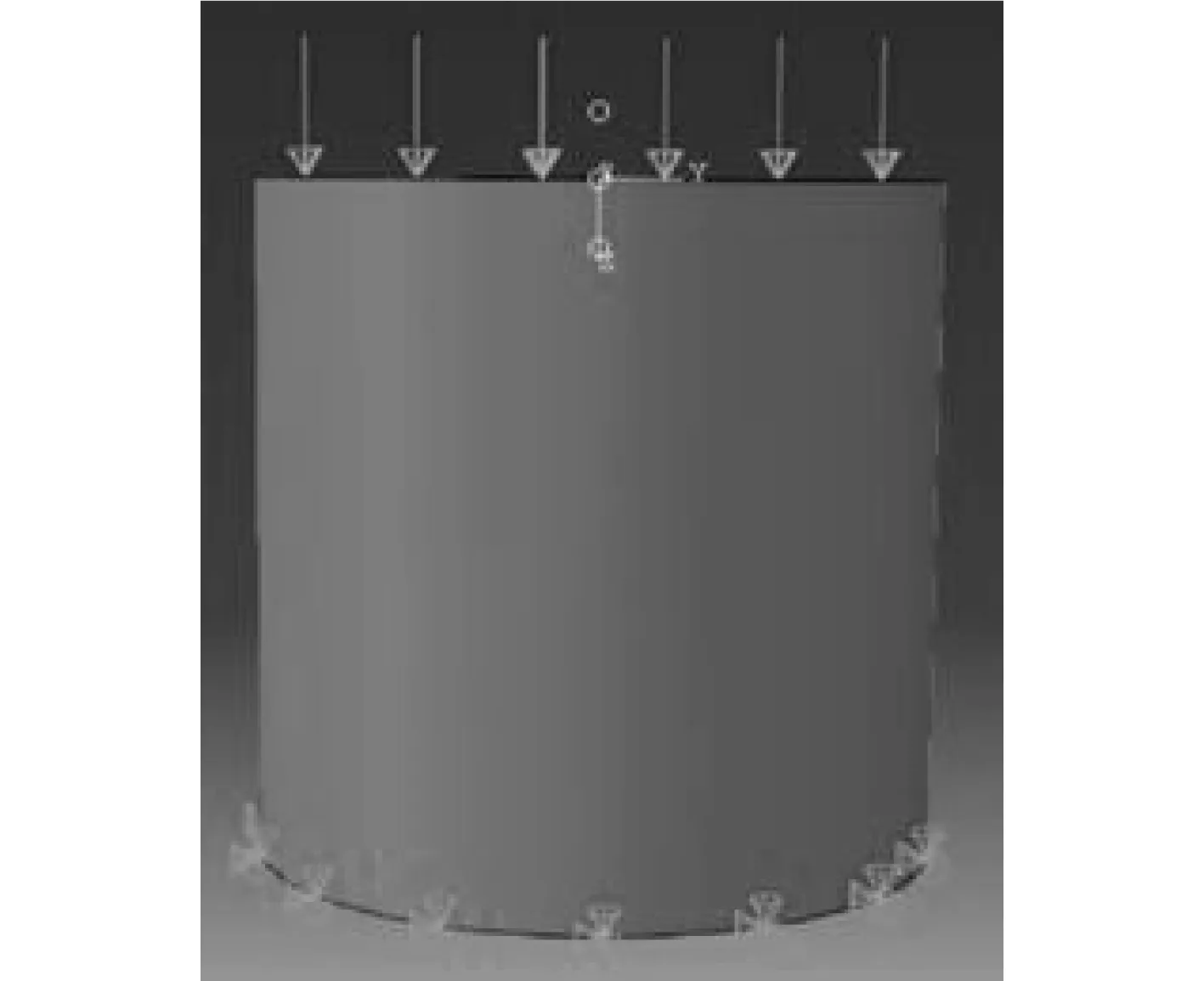
图2 边界条件Fig. 2 Boundary conditions
经过有限元仿真计算,得到4 种不同材料体积单元的应力分布剖面图,如图3 所示。不同材料的Mises 应力的最大值和最小值如表2 所示。结果发现丁腈橡胶的最大Mises 应力值在4 组材料中最高,所以丁腈橡胶的作为体积单元柔性基体相比其他组有更好的抗压表现。

表2 4 种材料的Mises 应力最大值与最小值Tab. 2 Mises stress maximum and minimum values for 4 materials
1.2 纤维结构体积单元有限元分析
为对比有无纤维结构的材料力学性能,对具有螺旋纤维结构的体积单元进行有限元分析,探究螺旋纤维结构对材料力学性能的影响。
体积单元的柔性基体部分选择丁腈橡胶材料,而刚性纤维部分选择的是弹性模量较大的碳纤维。纤维半径为0.5 mm,螺旋圆的半径为3 mm,在软件中输入材料的弹性模量与泊松比,并将材料属性分别分配给2 个部件。纤维角度为42.5°的体积单元Mises 应力分布图如图4 所示,其中纤维结构见图1,碳纤维的弹性模量为2.1×105MPa,泊松比为0.307。
由图3 可知,在轴向载荷的作用下,应力大小由四周向中央递减,且弹性模量越大,递减的速度就越快。然而,根据图4 所示的特定界面应力云图可以看出:弹性模量更大的刚性碳纤维承受主要应力的区域在刚性纤维与弹性基体交界处,最大应力达67.7 MPa;螺旋结构的下侧应力集中要小于上侧,约为39.51 MPa。相比于刚性纤维,作为弹性基体的丁腈橡胶所受的应力则非常小,仅为0.047 MPa,而且基体的应力分布十分均匀,保证材料各处的磨损一致。通过与无纤维体积单元的应力分布进行对比,可以发现嵌入螺旋纤维结构的体积单元柔性基体承受的应力要小于其他3 种材料的无纤维结构体积单元中心区域的应力。

图3 4 种材料体积单元Mises 应力分布图Fig. 3 Mises stress distribution diagram of 4 kinds of material volume elements

图4 42.5°纤维结构体积单元Mises 应力分布图Fig. 4 Mises stress distribution diagram of 42.5° fiber structure volume unit
综合上述分析可知:
1)纤维结构对整个结构有支撑作用,提高了整个结构的抗压性能。
2)在表面载荷作用下,纤维可以承担大部分的应力载荷,基体几乎不会承受太大应力。
3)螺旋结构上下侧有较为明显的应力差,表明弹性基体对于纤维是有一定的支撑保护作用的。
为分析纤维结构布置角度对仿真结果的影响,建立2 个不同纤维角度的体积单元模型。2 个体积单元的纤维螺旋角分别为30°和40°,均小于用于分析的体积单元纤维角度(42.5°)。通过同样步骤分析,3 个纤维螺旋角度各种应力分析结果如表3 所示,3 个纤维螺旋角度各种应力分析曲线如图5 所示。
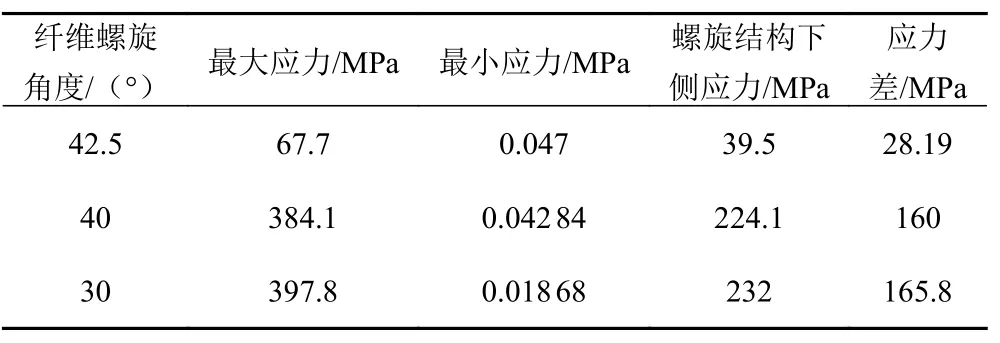
表3 3 个纤维螺旋角度各种应力分析结果Tab. 3 Various stress analysis results for three fiber helix angles
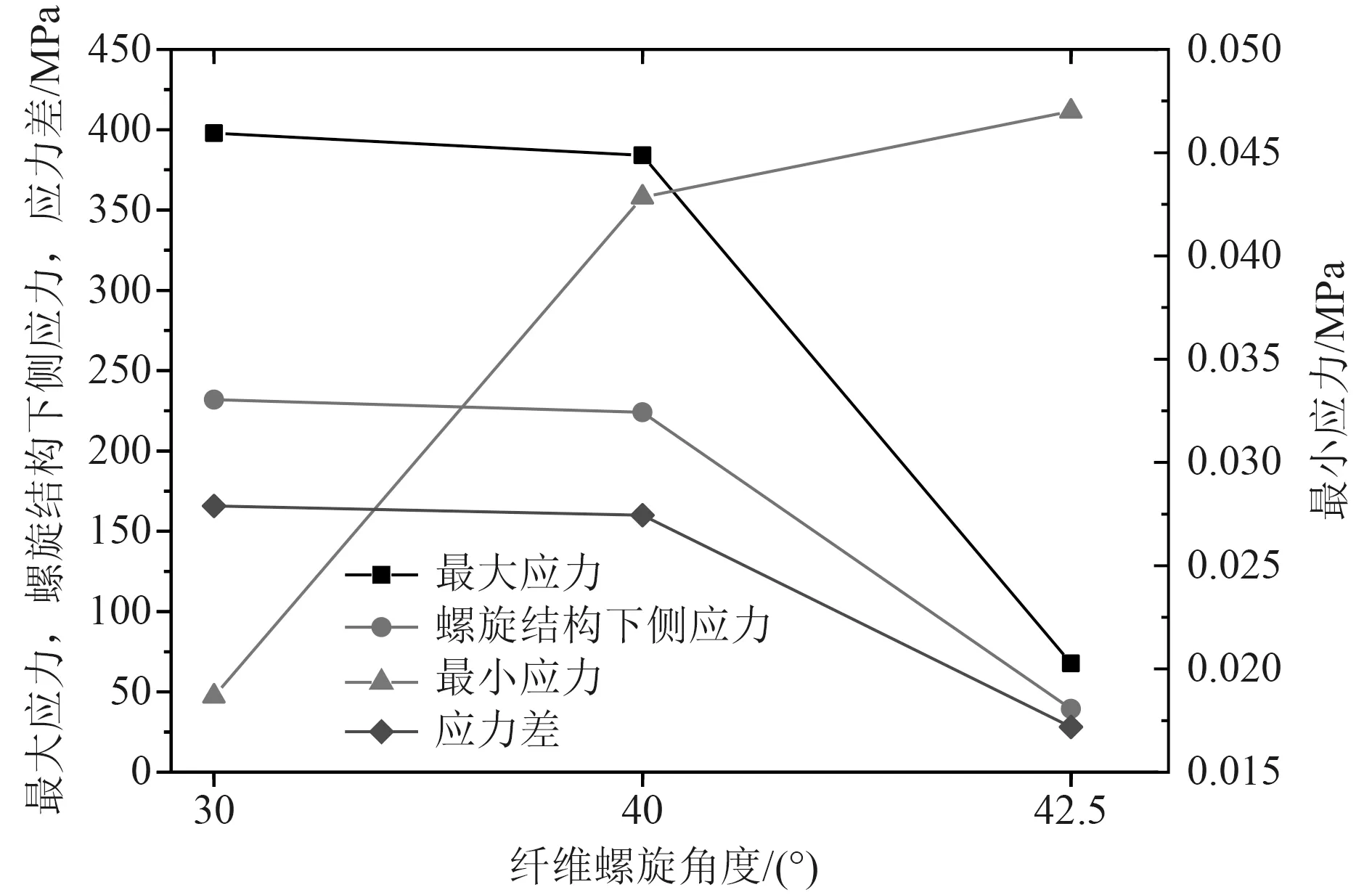
图5 42.5°三个纤维螺旋角度各种应力分析曲线Fig. 5 Various stress analysis curves of three fiber helical angles
根据图5 可以看出,纤维的螺旋角度对于体积单元的应力分布具有重要的影响。当纤维角越小时,最大应力最大,即刚性纤维将承受更大的应力,体积单元的整体抗压性能和刚度会提高,但是两相的应力差会增大,体积单元结构的韧性会下降。当增大纤维的螺旋角,使得刚性纤维承受的应力下降,影响了体积单元的抗压性能,最小应力也会提升,即较大的螺旋角可以保证柔性基体对于刚性纤维具有更好的支撑保护作用,增强了体积单元的韧性。因此,纤维螺旋角度大小要根据材料的性能要求进行选择,不同的性能要求选择不同的纤维螺旋桨角。
2 设计结构参数优化
2.1 纤维直径的优化
为探究刚性材料的比例对纤维结构力学的影响,通过改变纤维的半径控制刚性材料的占比,如图6 所示。建立4 组不同纤维半径的有限元模型进行对比分析。采用式(1)-(3)计算刚性材料占比,不同纤维半径的刚性材料占比如表4 所示。

图6 4 种半径纤维结构网络划分Fig. 6 Four kinds of radius fiber structure network division

表4 不同纤维半径下对应的刚性材料占比Tab. 4 The proportion of rigid materials corresponding to different fiber radii
式中:n为纤维数量;r1为 纤维半径;L为纤维螺距;d为螺旋圆直径;h为微结构圆柱体高度。
采用与之前一样的边界条件,使用Standard 求解器求解运算分别得到4 种纤维半径体积单元的应力分布,不同纤维半径下对应的最大和最小应力如表5 所示。将4 种半径下对应的应力绘制成曲线图,如图7 所示。
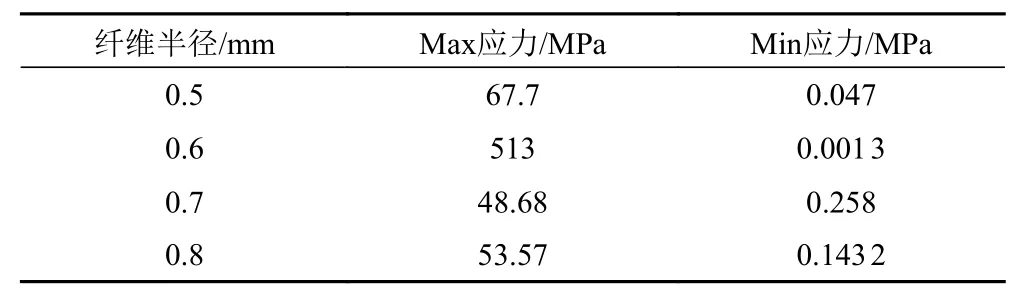
表5 不同纤维半径下对应的最大和最小应力Tab. 5 Maximum and minimum stresses corresponding to different fiber radii
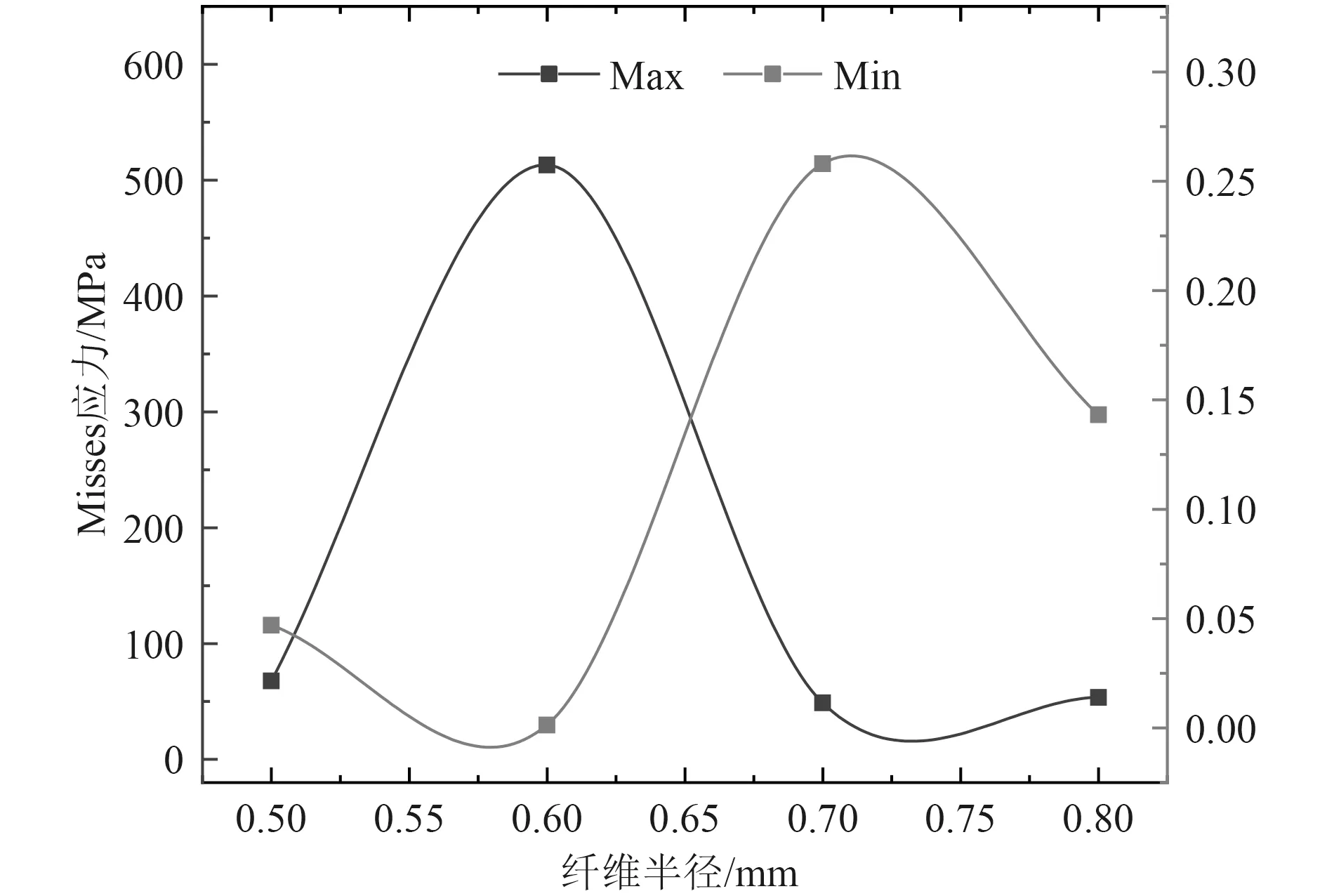
图7 不同纤维半径对应的最大应力与最小应力Fig. 7 Maximum stress and minimum stress corresponding to different fiber radii
从图7 可以看出:体积单元在没有被破坏的情况,当半径为0.6 mm 时,最大应力值达到峰值,即刚性纤维承受的应力值达到了峰值,之后开始下降,同时最小应力值此时最小,即柔性基体承受的应力值也达到了4 组数据中的最小值,之后开始上升;当半径为0.7 mm 时,刚性纤维承受的应力值最小,柔性集体承受的应力值最大;半径为0.7 mm 在图7 的半径范围内,体积单元力学性能最差。同时纤维半径为0.6 mm的体积单元在该实验条件下有最优的抗压力学性能。
3 结 语
本文主要介绍利用仿真软件优化刚柔异相结构体积单元的方式,并通过对比得出结论。
1)在表面载荷作用下,纤维结构可以承担大部分的应力载荷,弹性基体只承受很小的应力,证明了纤维结构对于体积单元具有支撑保护作用。
2)纤维螺旋角度大小要根据材料的不同性能要求进行选择,同时需要选择最优体积单元刚柔两相比例。根据本文仿真分析,同一载荷条件下,纤维螺旋角度30°、纤维半径为0.6 mm 时的体积单元力学性能最优。
3)同等载荷下,刚柔异相的纤维结构复合材料相较于传统的水润滑轴承材料具有更优秀的力学性能。
