Spectroscopic Determination of C,N,and O Abundances of Solar-analog Stars Based on the Lines of Hydride Molecules
2023-03-25YoichiTakeda
Yoichi Takeda
11-2 Enomachi,Naka-ku,Hiroshima-shi,730-0851,Japan;ytakeda@js2.so-net.ne.jp
Abstract Photospheric C,N,and O abundances of 118 solar-analog stars were determined by applying the synthetic-fitting analysis to their spectra in the blue or near-UV region comprising lines of CH,NH,and OH molecules,with an aim of clarifying the behaviors of these abundances in comparison with [Fe/H].It turned out that,in the range of-0.6 ≾[Fe/H]≾+0.3,[C/Fe] shows a marginally increasing tendency with decreasing [Fe/H] with a slight upturn around [Fe/H]∼0,[N/Fe] tends to somewhat decrease toward lower [Fe/H],and [O/Fe] systematically increases (and thus [C/O] decreases) with a decrease in [Fe/H].While these results are qualitatively consistent with previous determinations mostly based on atomic lines,the distribution centers of these [C/Fe],[N/Fe],and[O/Fe]at the near-solar metallicity are slightly negative by several hundredths of dex,which is interpreted as due to unusual solar abundances possibly related to the planetary formation of our solar system.However,clear anomalies are not observed in the[C,N,O/Fe]ratios of planet-host stars.Three out of four very Be-deficient stars were found to show anomalous[C/Fe]or[N/Fe]which may be due to mass transfer from the evolved companion,though its relation to the Be depletion mechanism is still unclear.
Key words: Galaxy:evolution–planet-star interactions–stars:abundances–stars:atmospheres–stars:solar-type
1.Introduction
Carbon (C),nitrogen (N),and oxygen (O) are representatively abundant light elements in the universe next to hydrogen and helium.They are synthesized or burned inside of a star and expelled at the last stage of stellar evolution out to the galactic gas,but the way this process occurs in which kind of stars is different for each element.While O is produced and distributed mainly by short-lived high-mass stars,longer-lived low-to-intermediate mass stars may also contribute to the enrichment of C or N.Therefore,CNO abundances in low-mass main sequence stars like our Sun can be a clue to studying the chemical evolution of these elements,because such stars have diversified ages and the composition of galactic gas at the time of star formation is retained in their atmospheres.Specifically,the runs of[C/Fe],[N/Fe],and[O/Fe]with a change of [Fe/H]1As usual,[X/H]is the differential abundance for element X of a star relative to the Sun defined as[X/H]≡A*(X)-A⊙(X),where A(X)is the logarithmic number abundance of element X(normalized with respect to H as A(H)=12).Likewise,the notation [X/Y] is defined as [X/Y]≡[X/H] -[Y/H].(representative of metallicity) in solartype stars2Although no definite classification scheme exists,the following terminology may hold as a rule of thumb: (1) “Solar-type stars” are late-type stars of solar associates in the broad sense (e.g.,early K through late F-type dwarfs or subgiants).(2) “Solar analogs” are early G-type dwarfs which have properties analogous to the Sun(e.g.,differences in Teff andlogg are±≾100–200 K and±≾0.1–0.2 dex).(3) “Solar twins” apply to a special group of stars with parameters very resembling the Sun (e.g.,ΔTeff and Δlogg are within a few tens of K and within a few hundredths of dex respectively).play an important role in this context.
Given this astrophysical significance,many spectroscopic determinations of CNO abundances for solar-type stars have been carried out so far (e.g.,Takeda &Honda 2005,and the references therein).However,it is not necessarily easy to yield a sufficient precision.For example,in the work of Takeda &Honda(2005),C or O abundances derived from permitted and forbidden lines were not in satisfactory agreement.Actually,several disadvantages are involved in using lines of neutral atoms(C I,N I,O I)usually adopted:(i)Usable lines are rather few in number and do not have sufficient strengths.(ii) Many are high-excitation lines and thus considerably dependent uponT(temperature) in late-type stars.(iii) Though forbidden lines([C I] or [O I]) are inert toT,they are so weak and apt to be contaminated by blending.(iv) Stronger lines existing in the near-infrared (near-IR) region tend to suffer a considerable non-local thermodynamic equilibrium (non-LTE) effect.
In the meantime,another possibility of CNO abundance determinations is to make use of lines of hydride molecules(CH,NH,and OH) in the blue or near-ultraviolet (near-UV)region,which however has not been mainstream,because this task comes with several difficulties:(i)These lines are in rather unfavorable wavelength regions (accessibility,line crowdedness,etc.).(ii) Since the classical analysis using line-by-line equivalent widths is hardly practicable,it is requisite to compare the observed and theoretically synthesized spectra.(iii) Because of low dissociation potentials,the populations of these molecules are quite sensitive toT,which means that resulting abundances are appreciably dependent upon adopted atmospheric models.(iv) More seriously,abundances (A)derived from these molecular lines(especially those of the UV region such as NH)tend to suffer more or less systematic errors for unknown reasons,as shown by the pioneering work of Laird (1985).
However,although such systematic errors involved inA(X) (X=C,N,O) derived from hydride molecules may be unavoidable,differential abundances relative to the Sun([X/H];see footnote 1)may still be acceptable at least for solartype stars,because errors tend be canceled if stars are not much different from the Sun.Actually,several studies revealed that reasonable results of [X/H] could be obtained for FGK-type dwarfs (including planet-host stars) by applying the spectrum synthesis analysis to molecular line features in the blue–UV region;e.g.,Ecuvillon et al.(2006)for OH,Suárez-Andrés et al.(2016) for NH,and Suárez-Andrés et al.(2017) for CH.
If so,it must be more preferable to carry out a differential analysis relative to the Sun exclusively for“solar-analog”stars(Sun-like early G-type dwarfs;see footnote 2),by which systematic errors would be largely suppressed.Therefore,sufficient reliability is expected for the differential abundances([X/H]) of solar analogs;moreover,high precision would be accomplished by averaging the results derived from a number of spectral regions(thanks to the availability of numerous lines for these molecules).
The author’s group previously carried out comprehensive investigations for 118 solar-analog stars in comparison with the Sun,which were published in a series of papers: Takeda et al.(2007) (stellar parameters and Li abundances),Takeda et al.(2010) (stellar activity estimated from Ca II 8542 and its relation to rotation),Takeda et al.(2011) (behaviors of Be abundances determined from Be II 3131),and Takeda et al.(2012) (detection of low-level activity using Ca II 3934).In connection with this project,we acquired high-dispersion spectra of near-UV through the blue region (∼3000–4600 Å)for all of the sample stars,which were employed for the latter two studies.Since these spectra are just suitable for doing the differential analysis of molecular lines mentioned above,I decided to conduct new CNO abundance determinations of these solar analogs based on CH,NH,and OH lines,while paying attention to the following points.
1.How do [C/Fe],[N/Fe],and [O/Fe] behave with a change of [Fe/H] (e.g.,gradient,dispersion,zero-point)within±several tenths of dex around [Fe/H]∼0? It is interesting to compare their trends with those previously derived from atomic lines.The variation of [C/O] with[Fe/H] is also an important checkpoint.
2.Do stars harboring giant planets manifest any appreciable difference in terms of CNO abundances in comparison with the sample of non-planet-host stars?
3.Takeda et al.(2011) serendipitously found four extraordinary Sun-like stars,in which Be is drastically deficient by ≿2 dex compared to the others (and the Sun).It is interesting to check whether these Be-depleted stars exhibit any peculiarities in CNO abundances,which may provide some information on the origin of the Be anomaly.
The purpose of this article is to describe the outcome of this analysis.
2.Program Stars
2.1.Atmospheric Parameters
The sample of 118 solar-analog stars in the solar neighborhood is the same as that adopted in Takeda et al.(2007),which was selected by the criterion of 0.62 ≾B-V≾0.67 and 4.5 ≾MV≾5.1 (centered around the solar values of(B-V)⊙=0.65 andMV⊙=4.82).Likewise,regarding the atmospheric parameters [Teff(effective temperature),logg(surface gravity),vt(microturbulence),and [Fe/H] (Fe abundance relative to the solar Fe abundance ofA⊙(Fe)=7.50)]of these stars along with the Sun,those spectroscopically determined by Takeda et al.(2007) (standard solutions;see Section 3.1.1 therein) were used unchanged.3Exceptionally,the parameters for HIP 41484 derived in Takeda et al.(2007)were wrong,because irrelevant observational data were erroneously used for this star.The correct parameters were later redetermined in Takeda et al.(2010)(see Appendix A therein).The list of 118 stars(+Sun)and their atmospheric parameters are presented in Table 1,where 12 planet-host stars4According to “The Extrasolar Planets Encyclopaedia” site (http://exoplanet.eu/).This number has significantly increased since the time of Takeda et al.(2011),where only 5 stars out of these 118 solar analogs were regarded as planet-harboring stars (see Section 4.1.3 therein).and 4 Be-depleted stars(see Section 4.2 in Takeda et al.2011) are also indicated.The atmospheric models are the same as those adopted in our previous papers(see Section 4.1 of Takeda et al.2007),which were generated by three-dimensionally interpolating Kurucz’s(1993a) ATLAS9 grid of model atmospheres in terms ofTeff,logg,and [Fe/H] (metallicity).
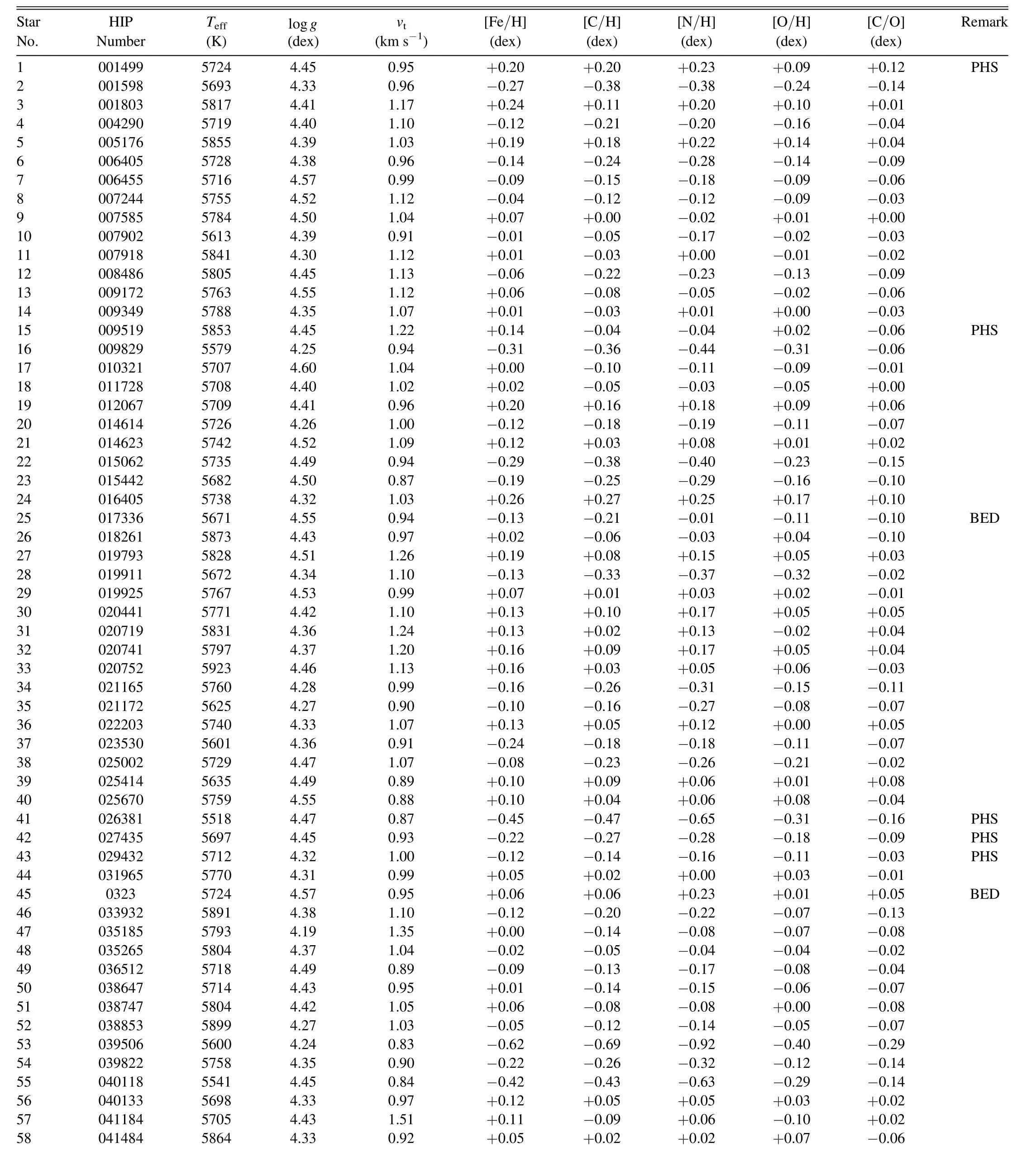
Table 1 Stellar Parameters and the CNO Abundance Results of 118 Program Stars
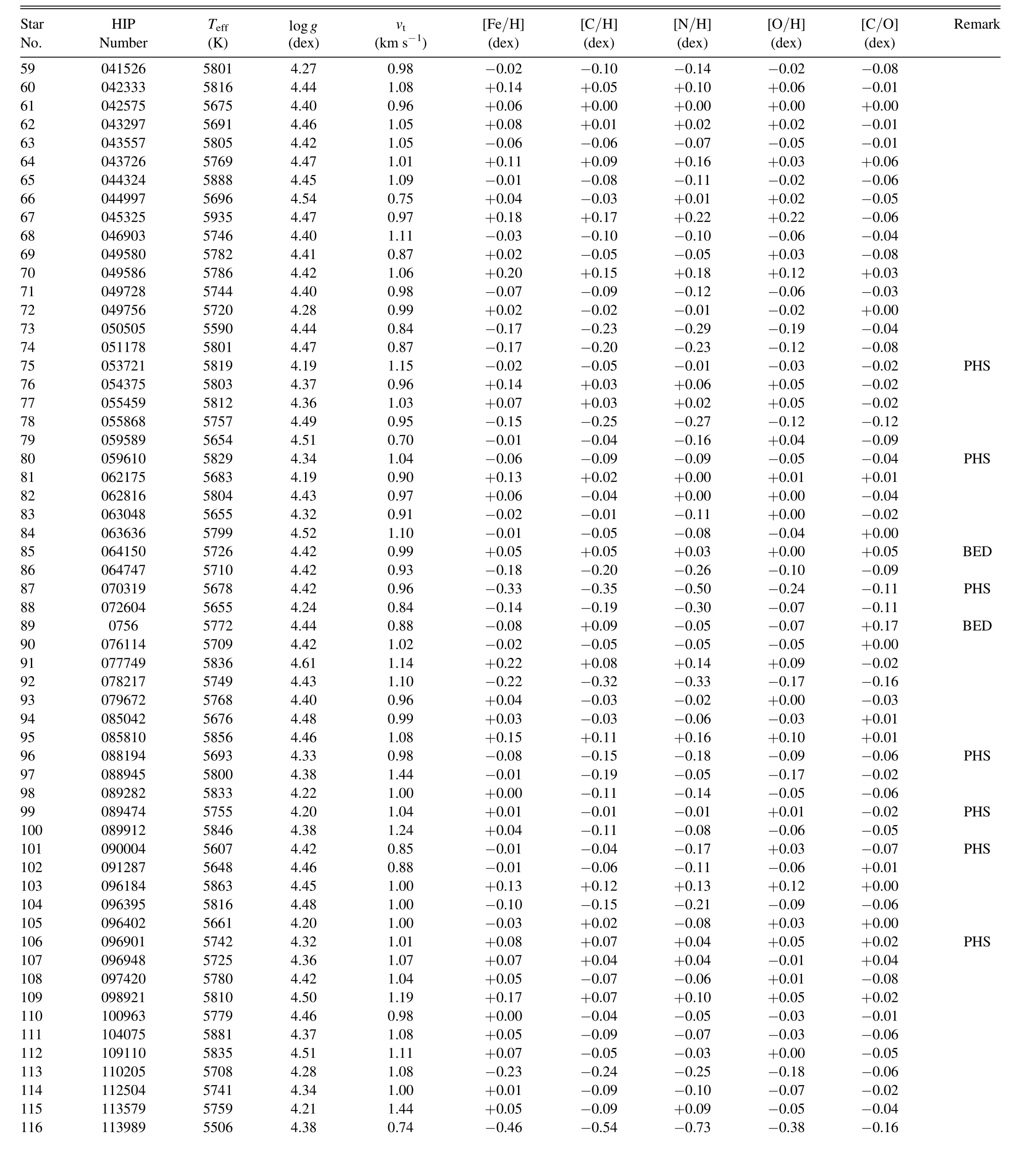
Table 1 (Continued)

Table 1 (Continued)
2.2.Errors in Teff,log g,and vt
As described in Section 3.1.1 of Takeda et al.(2007),these atmospheric parameters were determined by using the TGVIT program (Takeda et al.2002,2005) based on the equivalent widths of Fe I and Fe II lines,while requiring three conditions to be simultaneously satisfied: (a) independence ofA(Fe)upon χlow,(b) independence ofA(Fe) upon the equivalent widths,and(c)matching the mean abundances of〈A(Fe I)〉and〈A(Fe II)〉.Since solargfvalues (see Section 2 in Takeda et al.2005)were adopted in this application to solar-analog stars,the statistical errors involved inTeff,logg,andvt(estimated by the procedure described in Section 5.2 of Takeda et al.2002) aresufficiently small,which are typically on the order of ∼±20 K,∼±0.05 dex,and ∼±0.1 km s-1,respectively.See also Section 3.4 in Takeda et al.(2011);the errors derived for individual stars are given in electronic table E3 of that paper.
2.3.Observational Data
The high-dispersion spectra of 118 program stars and Vesta(substituting for the Sun) covering ∼3000–4600 Å with a resolving power ofR≃60,000 used in this study are those obtained in 2009–2010 with the High Dispersion Spectrograph (HDS) placed at the Nasmyth platform of the 8.2 m Subaru Telescope atop Maunakea(see Section 2 of Takeda et al.2011 for more details).
3.Abundance Determination
3.1.Method of Analysis
Since the near-UV through blue spectral regions comprising lines of CH,NH,and OH molecules are considerably crowded with lines,abundance determination should be done by comparing the observed and theoretically synthesized spectra with each other.For this purpose,Takeda’s (1995) automatic spectrum-fitting technique was applied by employing the MPFIT program written by Y.Takeda based on Kurucz’s(1993a) WIDTH9 code.This method aims to match the observed (flux) spectrum in an arbitrary scale () with the theoretical flux,which is a function of various parameters;e.g.,wavelength shift (Δλ),macrobroadening velocity (vM:efolding half-width of the Gaussian macrobroadening function,,elemental abundances (A1,A2,…),etc.In addition,two temporary parameters for adjustingare also included:C(scale control;see Section 2 in Takeda 1995) and β (tilt control;see footnote 3 in Takeda &Tajitsu 2014).The final solutions yielding the best match between theory and observation are obtained by numerically searching the multi-parameter space by applying the Newton–Raphson algorithm.Note that this method does not require any necessity of normalizing the observed spectrum by the local continuum in advance,which is a distinct merit because precisely placing the continuum level is very difficult in the present case.
In order to fit the line features of XH molecules(X=C or N or O),a depth-independent scale factor φ(XH)was introduced,by which the number population of XH molecules (computed from a model atmosphere with the metallicity-scaled X abundanceAmodel(X)) is to be multiplied to reproduce the observed XH line strengths.Then,the X abundance of a starA(X)was assumed to relate with φ(XH)asA(X)=Amodel(X)+logφ(XH).Note that this implicitly assumes that the population of XH is proportional to the composition of X,which is practically valid in the atmospheric condition of solar-analog stars where the number population of XH molecules is only a minor fraction of the total number of X nuclei(i.e.,most are in the form of neutral atoms).
3.2.Spectral Regions and Line Data
The spectral regions comprising CH,NH,and OH lines,where the fitting analysis for abundance determination is performed,were selected after exploratory test runs at 4270–4330 Å (CH),3340–3390 Å (NH),and 3100–3200 Å(OH).The finally adopted regions(12,11,and 11 for CH,NH,and OH respectively;each being typically ∼0.5–2 Å wide)are summarized in Table 2.This table also contains the elements whose abundances were varied (along with Δλ andvM) in the iterative analysis,while the abundances of all other elements were fixed at the metallicity-scaled solar abundances.
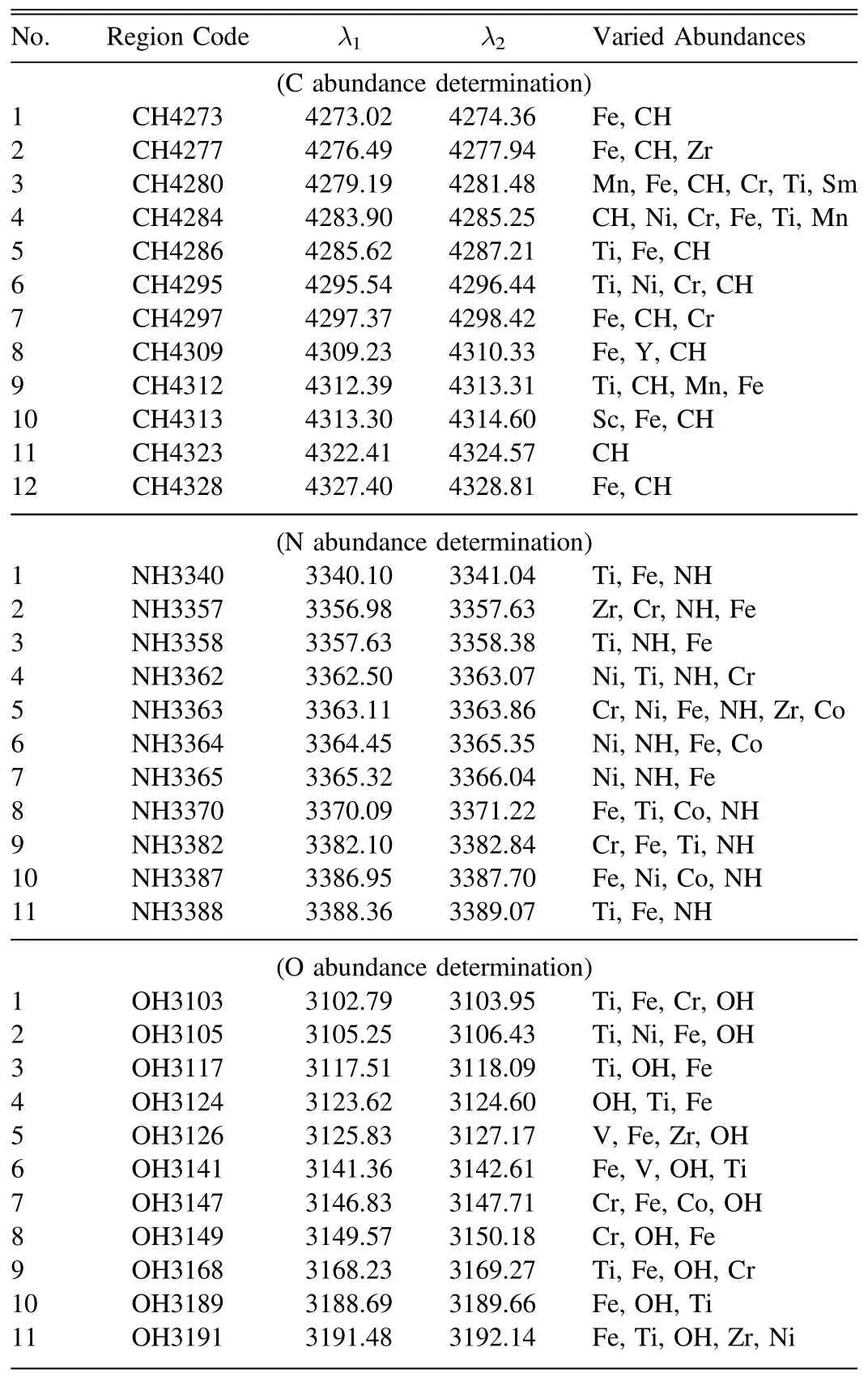
Table 2 Adopted Regions and Varied Abundances in the Fitting Analysis
Regarding the molecular line data of CH,NH,and OH in these regions,the files “ch.asc,” “nh.asc,” and “oh.asc”downloaded from Kurucz’s homepage (http://kurucz.harvard.edu/linelists/linesmol/) were invoked.Theloggfvalues in these files were further scaled with the standard isotope ratios by using Kurucz’s (1993b) “RMOLEC.FOR” program.Meanwhile,the data of atomic lines were taken from the VALD database (Ryabchikova et al.2015).In case that damping parameters are not available,the default treatments used in Kurucz’s (1993a) WIDTH9 program were employed.The finally adopted line data are presented as the supplementary electronic data (directory “linedat”;see Appendix).
As to the dissociation potentials (D0),the data already incorporated in the WIDTH9 code were adopted for CH(3.465 eV) and OH (4.392 eV) unchanged,which are almost the same as used by Suárez-Andrés et al.(2017)and Ecuvillon et al.(2006),respectively.However,D0for NH was replaced by 3.37 eV (instead of the original 3.47 eV) according to Suárez-Andrés et al.(2016).
3.3.Analysis Results
The iterative solution converged successfully in most of the 34 (=12+11+11) regions for the 118 stars as well as the Sun(Vesta),though some parameters(abundances orvM)had to be fixed in exceptional cases (especially for broader-line stars of comparatively higher rotational velocity) in order to avoid instability or divergence.
How the theoretical spectrum for the converged parameter solutions match the observed one is illustrated for each of the spectral regions in Figures 1(CH),2(NH),and 3(OH)for the case of the Sun.(The information regarding which lines of which species contribute to the complex spectral features of these figures may be found from the line data files in the directory “linedat” mentioned in Section 3.2;i.e.,line-tocontinuum opacity ratios η computed for all lines are useful.)Similar figures showing the resulting spectrum fit for all 118 stars and the relevant data of observed/theoretical spectra are presented as the supplementary electronic data (directories“fitfigs” and “specdat”;see Appendix).
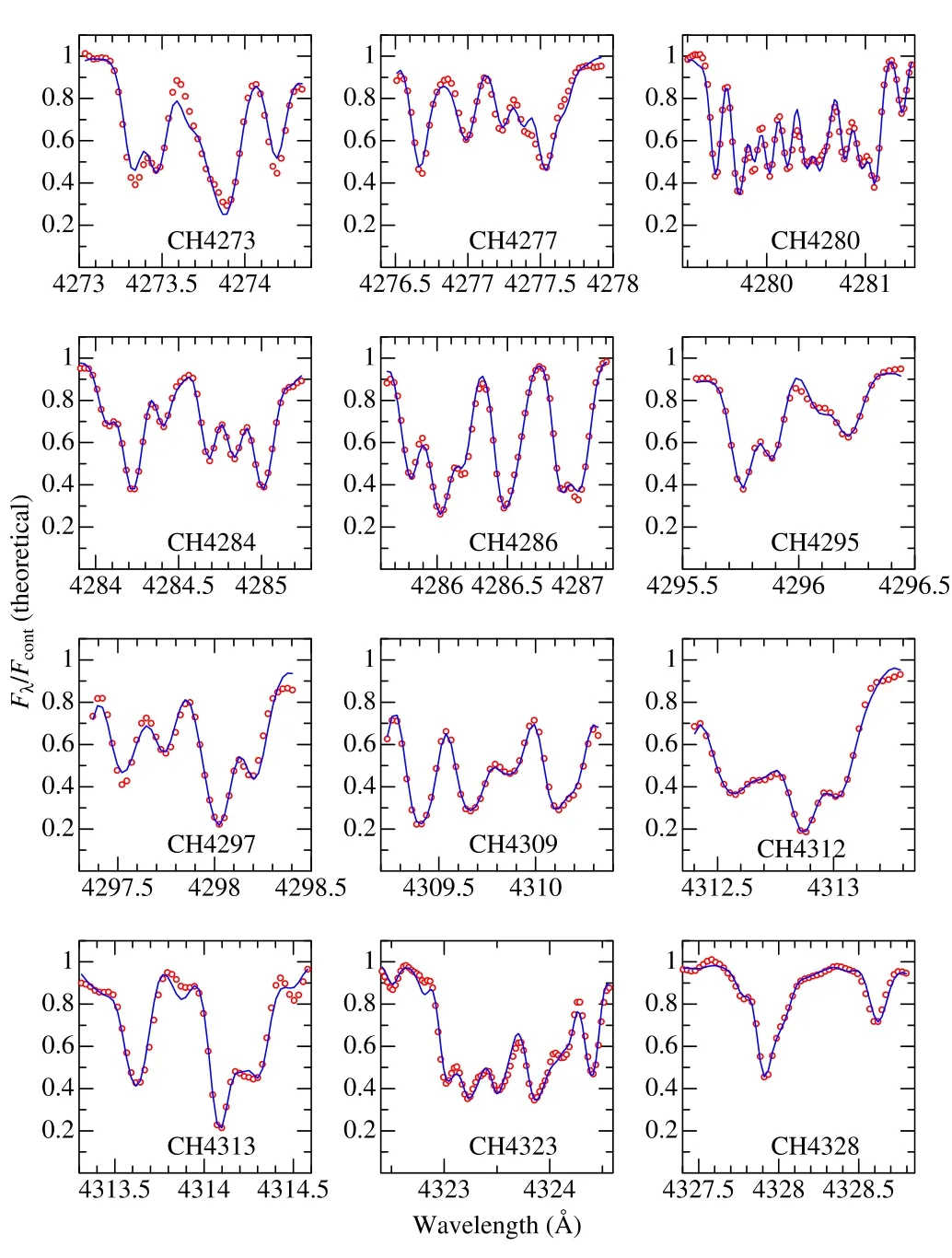
Figure 1.Observed and fitted theoretical spectra in each of the 12 regions(within 4270–4330 Å),where C abundances were determined from CH lines.Shown here is the representative case of the solar (Vesta) spectrum.The observed and theoretical spectra are depicted by red open symbols and blue lines,respectively.The corresponding region code(see Table 2)is specified in each panel.The wavelength scale of the spectrum is adjusted to the laboratory frame,and thescale marked in the left ordinate corresponds to the theoretical residualflux().

Figure 2.Observed and fitted theoretical solar spectra in each of the 11 regions(within 3340–3390 Å),where N abundances were determined from NH lines.Otherwise,they are the same as in Figure 1.
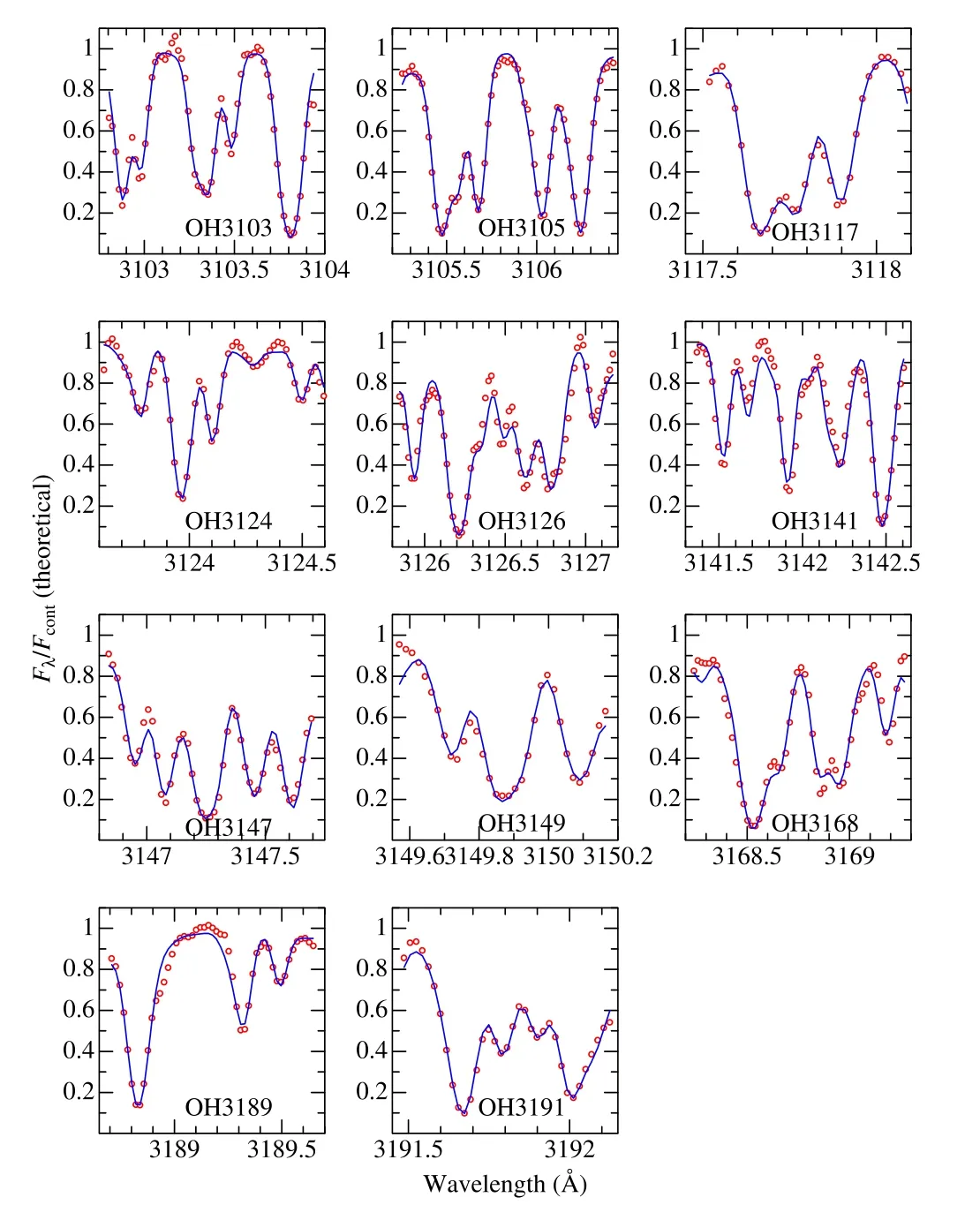
Figure 3.Observed and fitted theoretical solar spectra in each of the 11 regions(within 3100–3200 Å),where O abundances were determined from OH lines.Otherwise,they are the same as in Figure 1.
The resulting CNO abundances for the Sun [A⊙(C),A⊙(N),andA⊙(O)] derived for each region are displayed together in Figure 4,where the reference solar abundances taken from two compilations (Anders &Grevesse 1989;Asplund et al.2009)are also shown for comparison.We can see from this figure that CH,NH,and OH lines in the blue or near-UV region tend to yield more or less lower abundances (especially for N and O),as compared to the actual values.This is the tendency already found by Laird (1985) (see Section 1).The reason for this systematic error is not clear,for which several possibilities may be considered;such as missing opacity,overdissociation,threedimensional (3D) effect,etc.In any event,this problem involving the absolute scale ofAis irrelevant in the present case,because we aim to do a purely differential region-byregion analysis relative to the Sun.
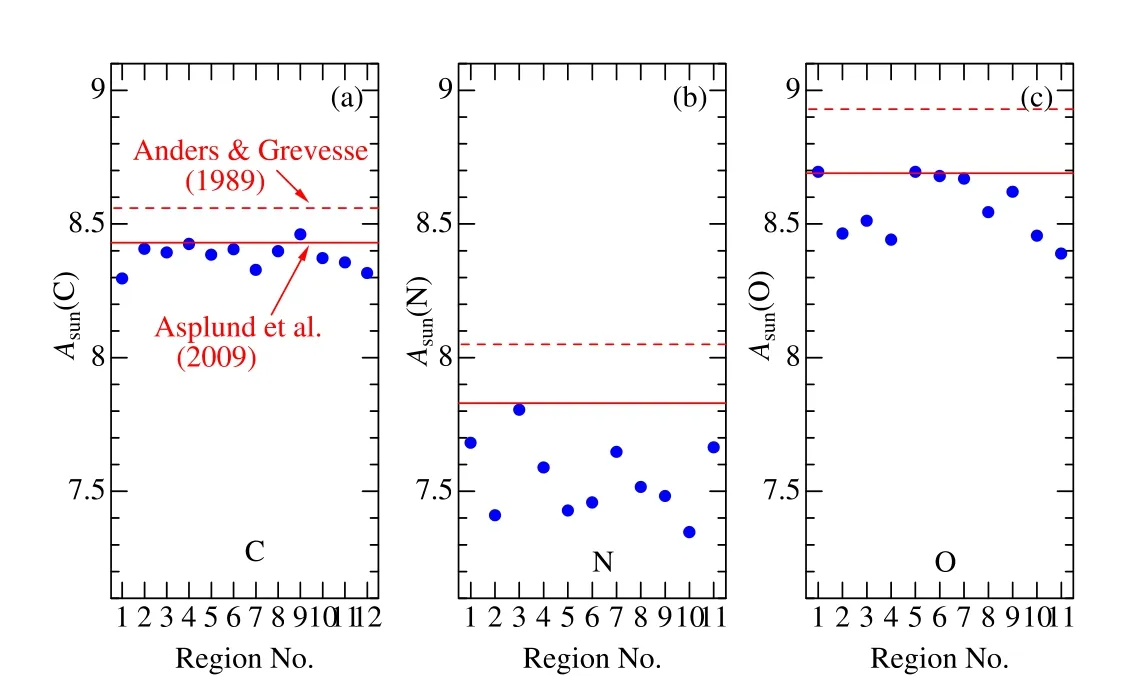
Figure 4.The results of C,N,and O abundances for the Sun(A⊙;logarithmic number abundance in the usual normalization of AH=12),which were derived from the fitting analysis of solar (Vesta) spectrum in each region,are plotted against the corresponding region number.The left,middle,and right panels are for C,N,and O,respectively.The reference solar CNO abundances published by Anders &Grevesse (1989) (8.56,8.05,8.93) and Asplund et al.(2009)(8.43,7.83,8.69) are indicated by the horizontal dashed and solid lines,respectively.
3.4.Mean Abundances and their Errors
Let the abundance of X(=C or N or O)derived from regionibeA*i(star) orA⊙i(Sun).Then,the mean differential abundance relative to the Sun averaged over the available regions is defined as
wherensis the number of selected regions finally used for averaging.5This number may be equal to or smaller than the total number of regions(nt=12,11,and 11 for C,N,and O),because outlier[X/H]i values judged by Chauvenet’s criterion were rejected.Since the standard deviation around this mean is
the mean error involved in 〈[X/H]〉 is written as
Figure 5(upper nine panels)plots the dispersion of each[X/H]iaround 〈[X/H]〉 and the extent of mean error (±∊) for all 118 stars,while the distribution histograms of ∊are illustrated in the bottom three panels.As seen from these histograms,most ∊values are within ≾0.01–0.02 dex,although several stars(mostly those with broader lines) exceptionally show larger ∊amounting up to ∼0.03–0.04 dex.Actually,mean ∊values averaged over all stars are (〈∊C〉,〈∊N〉,〈∊O〉)=(0.007,0.011,0.011)dex.The detailed results of each region’s [X/H]i,〈[X/H]〉,σ,and ∊(X=C,N,O) for all the program stars are summarized in the files “relabs_ch.dat,” “relabs_nh.dat,” and“relabs_oh.dat” (placed in the directory “abunds”) of the supplementary material (see Appendix).
Another error source we have to take into consideration is ambiguities in the atmospheric parameters.As mentioned in Section 2.2,the typical statistical errors involved inTeff,logg,andvtare ∼±20 K,∼±0.05 dex,and ∼±0.1 km s-1,respectively.In order to estimate the impact of these errors,the fitting analysis for the solar spectrum was repeated by perturbing these parameters interchangeably to see the resulting abundance changes (δT±,δg±,δv±) and their root-mean-square(δTgv).The results are depicted in Figure 6,which indicates that δTgvis essentially determined by δT±(reflecting the largeTsensitivity) and δTgvis typically ∼0.02–0.03 dex.As this δTgvacts rather similarly to each[X/H]i(i.e.,not random but in the same direction),〈[X/H]〉suffers also this amount of ambiguity due to parameter uncertainties (mainly determined by that ofT).
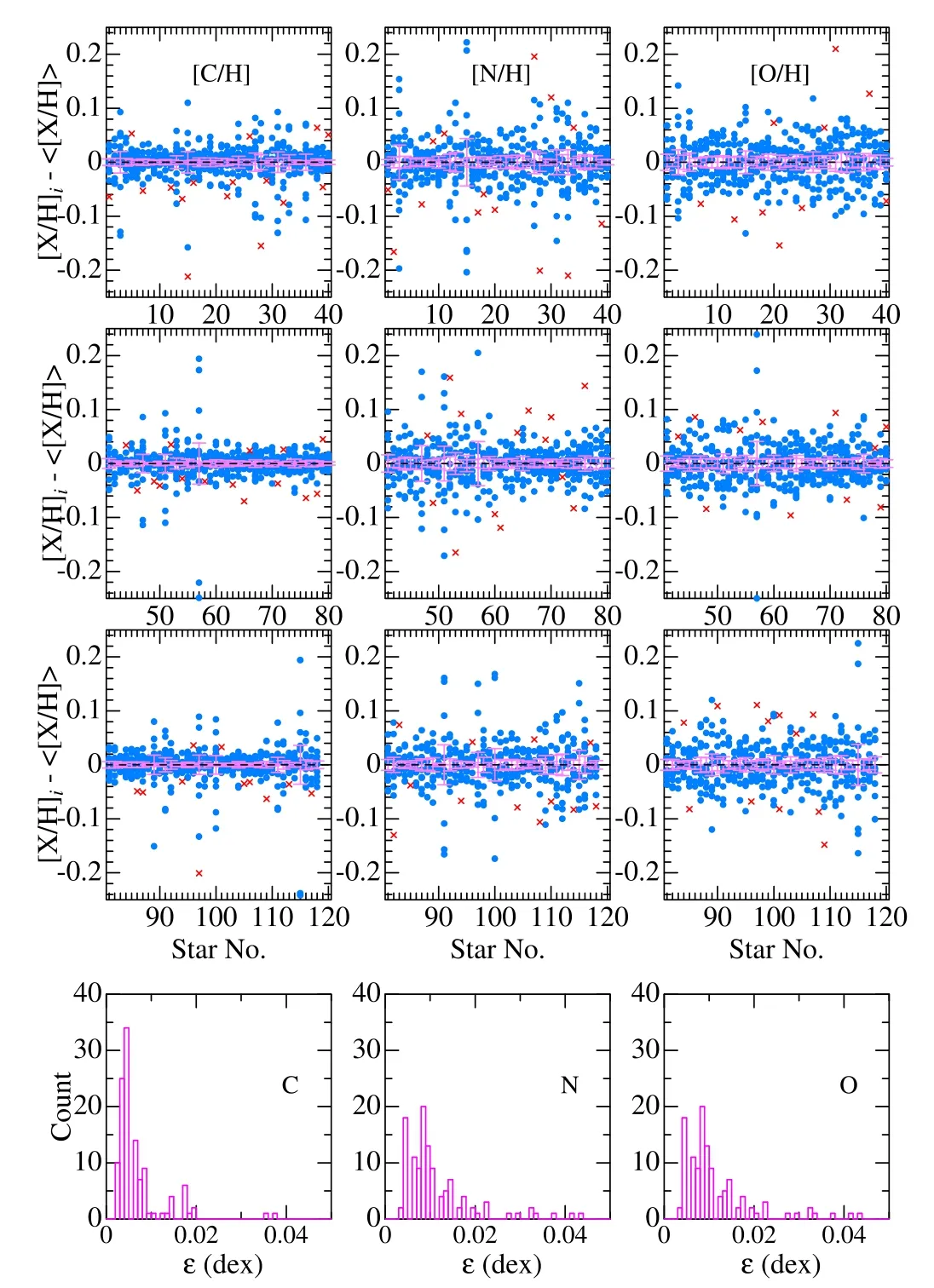
Figure 5.In the upper nine panels,differences between each [X/H] (X is C/N/O in the left/middle/right panels)of region i([X/H]i)and the mean[X/H]over the regions (〈[X/H]〉) are plotted (in blue symbols) for each of the 118 program stars,which helps to understand the extent of dispersion around the mean.The outlier values (judged by Chauvenet’s criterion) excluded from the averaging process are indicated by red crosses.The pink error bars show the size of mean error (±∊) of 〈[X/H]〉.In the lowest three panels are shown the distribution histograms for ∊.
Accordingly,combining these two kinds of errors (∊and δTgv),the typical extent of total error involved in 〈[X/H]〉would finally make ≾0.03 dex.
4.Discussion
4.1.CNO-to-Fe Abundance Ratios
Now that the relative abundances [X/H]6Hereinafter,the notation [X/H] is used to indicate 〈[X/H]〉 (mean value averaged over the regions) for simplicity.(X=C,N,O)have been established,we can examine the trends of [X/Fe](≡[X/H]-[Fe/H];logarithmic X-to-Fe abundance ratio)derived for solar-analog stars from hydride molecules in comparison with previous results,especially with those of Takeda &Honda (2005) determined for solar-type stars in a broader sense (FGK dwarfs/subgiants) by using atomic lines.How the resulting [X/H] and [X/Fe] are correlated with[Fe/H] (and also the mutual correlation between C and O) is displayed in the left and middle panels of Figure 7.The mean values averaged over each 0.1 dex bin of [Fe/H] between-0.3 ≤[Fe/H]≤+0.3 are illustrated in the right panels of this figure,where the corresponding Takeda &Honda (2005)results for FGK stars (derived from C I 5052/5380,N I 8680,and O I 7771–5 lines shown in their Figure 6) are also plotted for comparison.
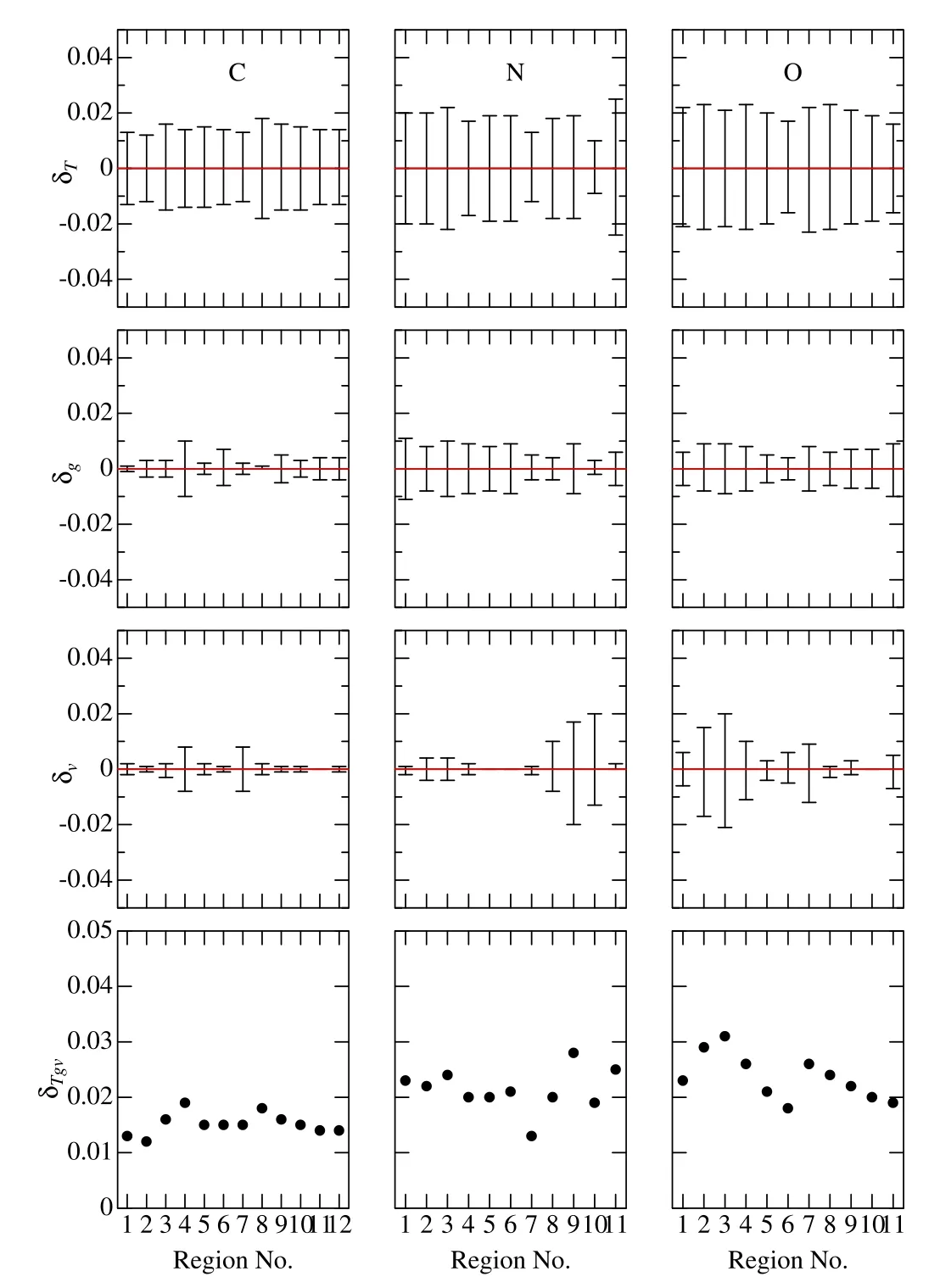
Figure 6.Effect of changing atmospheric parameters on the [X/H] result for each region calculated for the representative case of the Sun,where left,middle,and right panels are for C,N,and O,respectively;1st-row panels:δT+and δT-(abundance variations in response to Teff changes by±20 K);2nd-row panels: δg+ and δg- (abundance variations in response tologg changes by±0.05 dex);3rd-row panels: δv+ and δv- (abundance variations in response to perturbing the vt value by±0.1 km s-1);4th-row panels: root-sum-square of these three kinds of δʼs,which is defined as ,whereδT ≡(|δT+|+|δT-|)/2,δg ≡(|δg+|+|δg-|)/2,and δv ≡(|δv+|+|δv-|)/2.
We can see that [C/H] almost scales with [Fe/H](Figure 7(a)),while a systematic departure begins to appear for [N/H] (<[Fe/H];Figure 7(b)) and [O/H] (>[Fe/H];Figure 7(c)) with a decrease in [Fe/H].As a result,although[C/Fe] does not show so clear [Fe/H]-dependence(Figure 7(e)),[N/Fe] tends to decrease (Figure 7(f)) while[O/Fe] increases (Figure 7(g)) with a lowering of [Fe/H].Accordingly,[C/O](=[C/Fe]-[O/Fe])exhibits a progressive decrease toward lower metallicity (Figure 7(h)).The linearregression relations determined by the least-squares fit are[C/Fe]=-0.046(±0.032)[Fe/H]-0.067(±0.005),[N/Fe]=+0.242(±0.037)[Fe/H]-0.068(±0.006),[O/Fe]=-0.350(±0.027)[Fe/H]-0.035(±0.004),and[C/O]=+0.305(±0.025)[Fe/H]-0.031(±0.004),as depicted also in the relevant figure panels.
The slopes (d[X/Fe]/d[Fe/H]) of these relations are important in connection with the galactic chemical evolution.Yet,care should be taken in comparing them with other work,because the resulting gradient may depend upon how the sample stars are chosen.Particularly,since our solar-analog stars cover only a comparatively narrow metallicity range(most stars are within -0.3 ≾[Fe/H]≾+0.3),they are rather disadvantageous in this respect.Keeping this in mind,we may state that these trends are more or less in accord (at least qualitatively) with those published in previous studies;e.g.,Takeda&Honda(2005)for C and O(note that their results for N suffer large uncertainties and are thus unreliable),Ecuvillon et al.(2006) for O,Suárez-Andrés et al.(2016) for N,Suárez-Andrés et al.(2017)for C,Delgado Delgado Mena et al.(2021)for C/O,and the references therein.
Yet,some differences are noticeable from a quantitative point of view.Especially,the resultingd[C/Fe]/d[Fe/H]slope of-0.05 is apparently shallower than the previous values(e.g.,∼-0.2 concluded by Takeda&Honda 2005);but this is due to the fact that (i) the [Fe/H]-dependence of [C/Fe] is not linear but shows an appreciable upturn around[Fe/H]∼0 and(ii)the[Fe/H]range of our sample stars is narrow(±several tenths of dex around the solar metallicity).For this reason,the gradient for [C/Fe] (and [C/O]) derived here should not be taken seriously.
Meanwhile,attention should be paid also to the intercept values of these regression relations at [Fe/H]=0 (-0.067,-0.068,and-0.035 dex for C,N,and O respectively).That is,the center of gravity in the distributions of[C/Fe],[N/Fe],and[O/Fe] ratios around [Fe/H]∼0 is not zero but slightly negative by several hundredths of dex,which can also be recognized by eye-inspection of Figure 7(e)–(g) (or from Figure 7(i)–(k);blue bullet symbols).Since such a shift was not found in Takeda &Honda (2005) results for FGK stars (see pink bullets in Figure 7(i)–(k)),this detection is a consequence of high-precision relative abundances,which could be accomplished thanks to the effective differential analysis between the Sun and solar-analog stars.This zero-point offset in [C/Fe],[N/Fe],and [O/Fe] is a significant feature in relation to the status of our Sun among the solar-analog stars,as mentioned in the next Section 4.2.
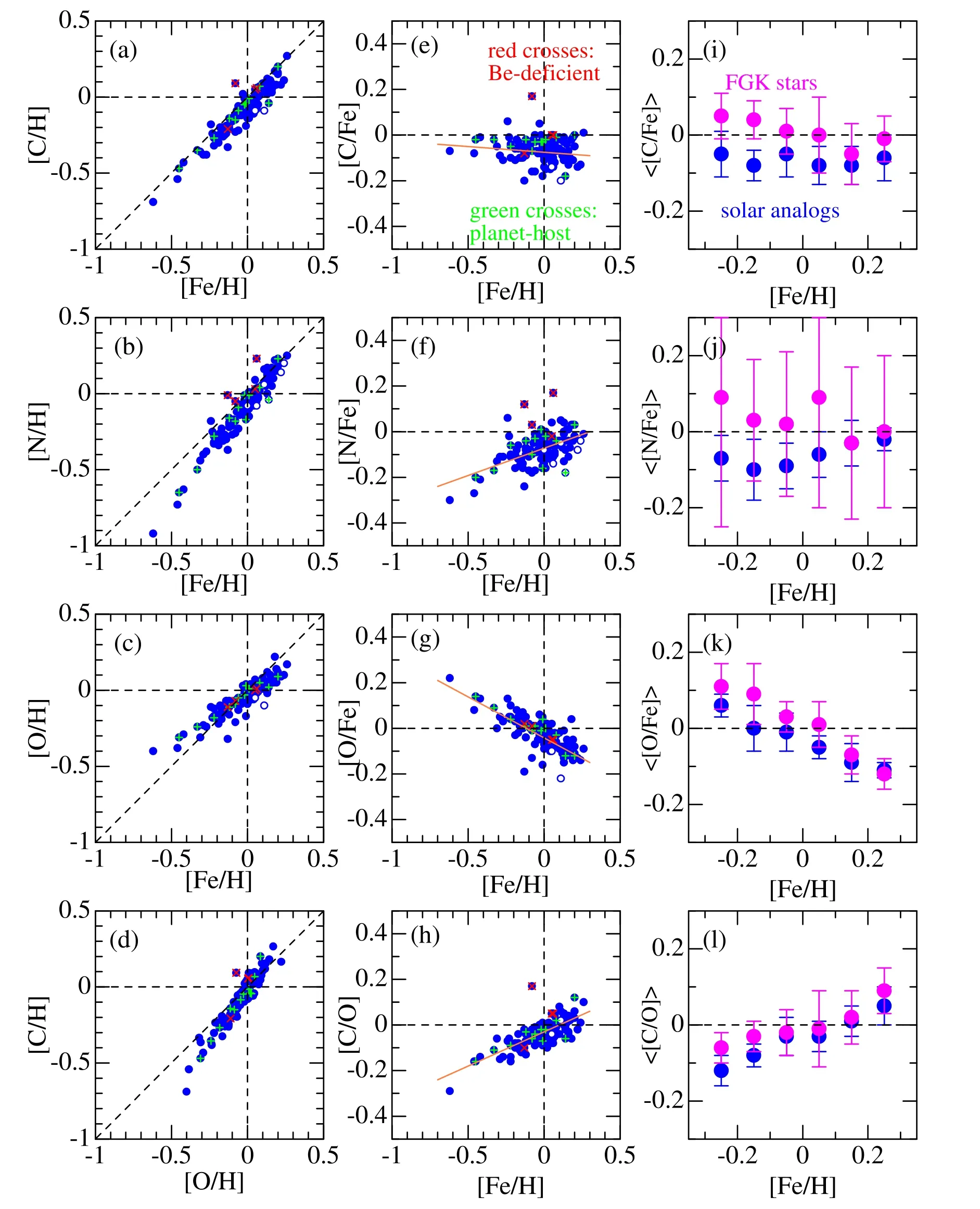
Figure 7.In the left-and middle-column panels are shown the correlations between[X/H](logarithmic abundance of element X relative to the Sun;X=C or N or O or Fe)and their differences(e.g.,[C/Fe]≡[C/H]-[Fe/H]):(a)[C/H]vs.[Fe/H],(b)[N/H]vs.[Fe/H],(c)[O/H]vs.[Fe/H],(d)[C/H]vs.[O/H].(e)[C/Fe]vs.[Fe/H],(f)[N/Fe]vs.[Fe/H],(g)[O/Fe]vs.[Fe/H],and(h)[C/O]vs.[Fe/H].Less reliable values(∊>0.03 dex)are indicated by open symbols;green crosses(+)and red crosses(×)are overplotted for 12 planet-host stars and 4 Be-deficient stars,respectively.In panels (e)–(h),the linear-regression lines determined by the least-squares analysis are also drawn by the orange solid lines.The bullet symbols in the right-column panels are the mean〈[X/Y]〉at each metallicity group(0.1 dex bin within-0.3 ≤[Fe/H]≤+0.3)determined for 118 solar analogs(blue,this study)and 160 FGK dwarfs(pink,Takeda&Honda 2005,the results displayed in their Figure 6)for comparison,where error bars signify the standard deviations (σ).Panels (i),(j),(k),and (l) are for 〈[C/Fe]〉,〈[O/Fe]〉,〈[N/Fe]〉,and 〈[C/O]〉,respectively.
4.2.Star–Planet Connection
In order to examine whether stars harboring giant planets show any difference in their CNO abundances,12 planet-host stars included in our 118 program stars are highlighted by overplotted green crosses in Figure 7(a)–(h).These figure panels do not reveal distinct differences between planet-host stars and no-planet samples (i.e.,most of the green crosses are distributed near the red linear-regression line showing the mean trend).Yet,some systematic tendency of[X/Fe](with planets)being slightly higher than [X/Fe] (without planets) might be seen (especially for [C/Fe] in Figure 7(e)).In order to check this point quantitatively,the difference (d)between [X/Fe]for each planet-harboring star and 〈[X/Fe]〉 (mean value in the relevant metallicity bin) was calculated and compared with σ(standard deviation of the distribution at the corresponding bin),as done by Takeda &Honda (2005) (see Section 5.2 and Table 3 in their paper).It then turned out that,while ∼70% of thedvalues of these stars are positive (i.e.,relatively overabundant trend on average),the deviations (d) do not exceed 1.5σ in most cases (d∼1.7 at the largest).This makes us feel that it is still premature to consider this trend as real.Further studies on a much larger sample of planet-host stars would be required to confirm or refute the reality of this suspected tendency.Accordingly,a conservative statement is retained for the time being that the photospheric CNO abundances of solar-analog stars are not significantly affected by whether they host giant planets or not.This conclusion is almost consistent with the consequences of Suárez-Andrés et al.(2016) for N,and Suárez-Andrés et al.(2017) for C.However,it does not lend support to Ecuvillon et al.(2006)’s argument for O that planet-host stars appear to show an oxygen overabundance by ∼0.1–0.2 dex in comparison with the reference sample.
As a topic relevant to the influence of planet formation upon photospheric abundances of a host star,the issue of zero-point offset in the[X/Fe]distribution at[Fe/H]∼0(see Section 4.1)has to be mentioned again.In order to ascertain the results described there,the [X/Fe] values in the near-solar metallicity range of -0.1 ≤[Fe/H]≤+0.1 (comprising 62 stars) were averaged,and the mean values (〈[X/Fe]〉) along with their mean errors (±∊) turned out to be 〈[C/Fe]〉=-0.063(±0.007),〈[N/Fe]〉=-0.070(±0.008),and 〈[O/Fe]〉=-0.033(±0.005),which are in agreement with the [Fe/H]=0 intercepts resulting from the linear-regression analysis in Section 4.1.Therefore,it is certain that these mean 〈[X/Fe]〉values are slightly negative (by ≃0.06–0.07 dex for C and N,≃0.03 dex for O) at [Fe/H]∼0.
As a matter of fact,this is closely related to the finding of Meléndez et al.(2009),who reported based on the highprecision differential analysis of 11 solar twins relative to the Sun that the Sun manifests a characteristic chemical signature.That is,the solar abundances of refractory elements (such as Fe) tend to be deficient relative to those of volatile ones (such as CNO)by ∼20%,in comparison with the reference sample of solar twins.This aspect may be associated with the formation mechanism of our solar system (especially rocky terrestrial planets).As seen from their Figure 2,when compared at the same solar metallicity,the volatile elements (CNO) in the Sun are comparatively overabundant than the average of solar twins by ≃0.05 dex (C),≃0.06 dex (N),and ≃0.03 dex (O),which implies that the mean 〈[X/Fe]〉 of the reference stars at [Fe/H]∼0 would turn out negative by these amounts.These offset values are satisfactorily consistent with our results.Accordingly,our analysis of 118 solar analogs based on the lines of CH,NH,and OH yielded essentially the same conclusion as they obtained from 11 solar twins (although the lines used for abundance determination are not explicitly described in their paper,C I,N I,and O I lines are likely to have been invoked as seen from the wavelength range of their spectra).
4.3.CNO Abundances of Be-dearth Stars
Takeda et al.(2011) reported that 4 stars out of 118 solar analogs(program stars of this study)are strikingly Be-depleted(by ≿2 dex).Actually,the lines of Be (and Li) are too weak and undetectable in these extraordinary stars (HIP 17336,32673,64150,and 75676).Soon after,Viallet &Baraffe(2012) investigated the impacts of rapid rotation and/or episodic accretion in the pre-main sequence phase (both may induce a global mixing,by which Li and Be are brought to the hot interior and burned out at temperatures of more than several million K) as a possible cause for such an extreme Be depletion.
From a different point of view,Desidera et al.(2016)pointed out that all these four peculiar solar analogs are binaries,and at least two of them (HIP 64150 and 75676) have white dwarf companions.This means that they may have suffered accretion of the nuclear-processed (Be-depleted) material from the evolved companion due to mass transfer events in the phase of red giant or asymptotic giant branch,which might be responsible for the Be anomaly.This thought lead Desidera et al.(2016) to study the chemical abundances of C andsprocess elements for these four stars in order to search for any signature of mass accretion from the companion.Interestingly,they found that HIP 75676 is an apparent barium star showing overabundances ofs-process elements (Y,Zr,Ba,La) and C.Therefore,in order to supplement their investigation,it is worthwhile to check the CNO abundances we have determined for these Be-depleted stars(which are marked by red crosses in Figure 7(a)–(h)).The following consequences can be drawn.
1.The[C/Fe]values derived by Desidera et al.(2016)from the CH band at 4300 Å (-0.12,-0.05,0.00,and +0.21 for HIP 17336,32673,64150,and 75676,respectively)are in reasonable agreement with our results (-0.08,0.00,0.00,and +0.17).
2.Appreciable anomalies deviating from the mean trend are seen in three cases for C and N (Figure 7(e) and (f)):HIP 75675ʼs [C/Fe] (=+0.17),HIP 17336ʼs [N/Fe](=+0.12),and HIP 32673ʼs [N/Fe] (=+0.17).In contrast,no peculiarity is seen in[O/Fe]for all four stars(Figure 7(g)).To sum up,three Be-depleted solar analogs(HIP 17336,32673,and 75676) show some kind of anomaly in either C or N,while HIP 64150 is quite normal in terms of CNO abundances.
3.As such,no conclusive evidence could be found for the tentative theory that considerable Be-depletion is caused by contamination of nuclear-processed materials from the companion.Although such an interaction event may have actually occurred in the past (especially for the barium star HIP 75676),the existence of a Be-deficient CNOnormal star(HIP 64150)indicates that the solution to this problem is not so simple.Moreover,as Desidera et al.(2016)pointed out,even if such an efficient mass transfer takes place in the binary system,it is quantitatively difficult to produce such a drastic Be depletion.
4.Accordingly,the question for the mechanism of depleting Be is still open.The role of mass transfer from the companion might have an indirect effect on the deficiency of Be (e.g.,induced thermohaline mixing or enhanced internal mixing triggered by episodic accretion),as discussed by Desidera et al.(2016).Also,we should pay attention to the possibility of Be-depletion caused by an effective mixing(e.g.,due to rapid rotation)in the pre-main sequence phase,as discussed by Viallet&Baraffe (2012).
5.Summary and Conclusion
Clarifying the behaviors of C,N,and O abundances(representative light elements processed in the stellar core to be dredged up and ejected outwards in the course of stellar evolution) in solar-type low-mass stars of diversified ages is important for studying the chemical evolution history of the Galaxy.
However,precisely establishing the key quantities [C/Fe],[N/Fe],and [O/Fe] (in comparison with the metallicity [Fe/H]) is not necessarily easy,because often adopted atomic C I,N I,and O I lines are small in number and generally weak.A possibility to ameliorate this situation is to invoke the lines of hydride molecules (CH,NH,and OH) numerously available with sufficiently large strengths in blue or near-UV wavelength regions.Although absolute abundances derived from these molecular lines are apt to suffer systematic errors,this problem can be circumvented by carrying out differential analysis relative to the Sun while limiting the sample only to solaranalog stars (early G-type dwarfs).
This consideration motivated the author to determine the C,N,and O abundances of 118 solar-analog stars,whose atmospheric parameters (Teff,logg,vt,and [Fe/H]) were already established by Takeda et al.(2007),based on the lines of hydride molecules in blue or near-UV regions.For this purpose,extensive spectrum-synthesis analyses based on the efficient automatic fitting algorithm were applied to 12 spectral regions of CH lines(selected from 4270 to 4330 Å),11 regions of NH lines(from 3340 to 3390 Å),and 11 regions of OH lines(from 3100 to 3200 Å).
The primary aims of this study were (i) to clarify the behaviors of [C/Fe],[N/Fe],and [O/Fe],(ii) to examine whether any abundance characteristics related to the existence of planets is seen,and(iii)to check whether any anomaly exists in the CNO abundances of four drastically Be-depleted stars found by Takeda et al.(2011).
The trends of[C/Fe],[N/Fe],and[O/Fe]in relation to[Fe/H] turn out almost consistent (at least qualitatively) with those reported by past studies mainly based on atomic lines: In the metallicity range of -0.6 ≾[Fe/H]≾+0.3,[C/Fe] exhibits a marginally increasing tendency for decrease of [Fe/H] with a slight upturn around [Fe/H]∼0,[N/Fe] tends to somewhat decrease toward lower [Fe/H],and [O/Fe] systematically increases (and thus [C/O] decreases) with decreasing [Fe/H].
It is noteworthy,however,that the centers of gravity of these[X/Fe]ratios(X=C,N,O)are slightly subsolar(negative)by several hundredths of dex (≃0.06–0.07 dex for C and N,≃0.03 dex for O)around[Fe/H]∼0,which may be interpreted as unusual CNO-to-Fe abundance ratios of the Sun (compared to the mean of other solar analogs).This is essentially a reconfirmation of the finding of Meléndez et al.(2009),who reported that refractory elements (such as Fe) are somewhat deficient relative to volatile ones (such as CNO) in the solar photosphere in comparison with the sample of 11 solar twins,which they suspected may be related to the formation mechanism of our solar system (especially rocky terrestrial planets).
In the meanwhile,regarding the question of whether CNO abundances suffer any influence by the existence of giant planets,clear differences are not seen in the distributions of[C/Fe],[N/Fe],and[O/Fe]for 12 planet-host stars in comparison to other no-planet samples,though a possibility of the former tending to be slightly larger than the latter cannot be ruled out.
Given that Desidera et al.(2016) reported that all four Bedepleted stars(HIP 17336,32673,64150,and 75676)detected by Takeda et al.(2011)are binary systems(in particular at least two stars have white dwarf companions),it is worthwhile to examine whether they have any CNO anomalies caused by contamination of nuclear-processed materials.Our results indicate that three of them (HIP 17336,32673,and 75676)show overabundances in either C or N,whereas HIP 64150 is quite normal in terms of CNO abundances.As such,mass transfer from the companion may have actually occurred in these stars (in particular,that is highly probable for the barium star HD 75676).However,it is premature to relate this to the cause of the Be anomaly,because it is quantitatively difficult for this mechanism alone to produce such a drastic Be depletion (by ≿2 dex).Accordingly,the question for the mechanism of depleting Be is still open.Several other interpretations such as those related to pre-main sequence evolution (Viallet &Baraffe 2012) or indirect effect of mass transfer from the companion (Desidera et al.2016) are worth further investigation.
Acknowledgments
This research is based on the data obtained by the Subaru Telescope,operated by the National Astronomical Observatory of Japan.This investigation has made use of the Kurucz database maintained by Dr.R.L.Kurucz,and the VALD database operated at Uppsala University,the Institute of Astronomy RAS in Moscow,and the University of Vienna.
Appendix Electronic Data Tables and Figures

Table A1 Contents of Line Data Files (“lines_??????.dat”)

Table A2 Contents of Abundance Data Files (“relabs_?h.dat”)
Supplementary electronic materials (data tables and figure files)accompany this article,which are separately contained in four directories as described below.
A.1.Atomic and Molecular Line Data
The directory “linedat” contains 34 files named“lines_??????.dat” (“??????” is the 6-character region code;e.g.,CH4273),which include the data of atomic and molecular lines (typically several hundred lines) used for the fitting analysis at each region.The data are basically arranged in ascending order of wavelength,though atomic and molecular lines are separately grouped in each file.Table A1 describes the contents of these line data.
A.2.Data of Observed and Theoretical Spectra
In the directory “specdat” are contained 34 files named“fit_??????.dat” (“??????” is the 6-character region code;e.g.,CH4273),which include the observed and fitted theoretical spectra at each region.Each file consists of 119 sections corresponding to 118 program stars and the Sun/Vesta (its number is tentatively designated as 999999).In each section,the first header line includes the information of 6-character HIP number(HIP),number of points(np),first wavelength(w1)and last wavelength (w2),which can be read with the format (2X,A6,I4,2F10.4).Then,λ (wavelength in Å),(observed spectra),and(fitted theoretical spectra) are given with the format (F8.3,2F10.4) in each of the followingnplines.Note that these spectra are the residual flux reduced to the theoretical continuum level ().
A.3.Figures of Spectrum Fitting
The directory“fitfigs”contains 34 PDF files named“??????.pdf” (“??????” is the 6-character region code;e.g.,CH4273),which include the figures showing the resulting fit between the observed (red open symbols) and theoretical (blue lines)spectra for each of the 118(+1) stars (constructed from the“fit_??????.dat” files).Each spectrum (indicated by the corresponding HIP number)is vertically shifted by 0.5 relative to the adjacent ones.Note that these figures are arranged in almost the same manner as adopted in our previous papers(e.g.,Figure 8 in Takeda et al.2007 or Figure 4 in Takeda et al.2011).
A.4.Abundance Results Derived for Each Region
Three data files “relabs_ch.dat,” “relabs_nh.dat,” and“relabs_oh.dat” are found in the directory “abunds”,which present the detailed results of relative abundances ([C/H] or[N/H] or [O/H] derived from each of the 11–12 spectral regions) and their means (along with the associated standard deviations and mean errors).Stellar parameters are also included for convenience.After the first header line,the results for each of the 118 stars are given in the 2nd through 119th lines,and the last 120th line is for the Sun/Vesta,where the absolute abundances [A(C) orA(N) orA(O)] resulting from each region (used as the reference abundances) are presented.The data contents and their format are described in Table A2.
ORCID iDs
杂志排行
Research in Astronomy and Astrophysics的其它文章
- Application of a Magnetic-field-induced Transition in Fe X to Solar and Stellar Coronal Magnetic Field Measurements
- Simulation-driven Wind Load Analysis and Prediction for Large Steerable Radio Telescopes
- Gravitational Wave Radiation from Newborn Accreting Magnetars
- Power-law Distribution and Scale-invariant Structure from the First CHIME/FRB Fast Radio Burst Catalog
- Solar Active Region Magnetogram Generation by Attention Generative Adversarial Networks
- Construction and Validation of a Geometry-based Mathematical Model for the Hard X-Ray Imager
