Construction and Validation of a Geometry-based Mathematical Model for the Hard X-Ray Imager
2023-03-25XianKaiJiangJianWuDengYiChenYiMingHuHaoXiangWangWeiLiuandZheZhang
Xian-Kai Jiang ,Jian Wu ,Deng-Yi Chen ,Yi-Ming Hu ,Hao-Xiang Wang ,Wei Liu ,and Zhe Zhang
1 Key Laboratory of Dark Matter and Space Astronomy,Purple Mountain Observatory,Chinese Academy of Sciences,Nanjing 210023,China;zhangzhe@pmo.ac.cn
2 School of Astronomy and Space Science,University of Science and Technology of China,Hefei 230026,China
Abstract Quantitative and analytical analysis of the modulation process of the collimator is a great challenge,and is also of great value to the design and development of Fourier transform imaging telescopes.The Hard X-ray Imager(HXI),as one of the three payloads onboard the Advanced Space-based Solar Observatory (ASO-S) mission,adopts modulating Fourier-Transformation imaging technique and will be used to explore the mechanism of energy release and transmission in solar flare activities.As an important step to reconstruct the images of solar flares,accurate modulation functions of HXI are needed.In this paper,a mathematical model is developed to analyze the modulation function under a simplified condition first.Then its behavior under six degrees of freedom is calculated after adding the rotation matrix and translation change to the model.In addition,unparalleled light and extended sources are also considered so that our model can be used to analyze the X-ray beam experiment.Next,applied to the practical HXI conditions,the model has been confirmed not only by Geant4 simulations but also by some verification experiments.Furthermore,how this model helps to improve the image reconstruction process after the launch of ASO-S is also presented.
Key words: instrumentation: detectors–Sun: X-rays–gamma-rays–techniques: image processing–methods:analytical
1.Introduction
The imaging observation in the hard X-ray band is of great significance for understanding the mechanism of energy release and transmission in solar flare activities.The Hard X-ray Imager (HXI) is a new hard X-ray telescope that applies the Fourier-transform (FT) imaging technique.As one of the indirect imaging instruments,it images the Sun by reconstructing from its pattern and measuring counting (Su et al.2019).So,an accurate pattern is a basis for high-quality imaging.However,the current methods of calculating patterns are either approximate or numerical,which affects the analyticity and efficiency of the imaging algorithm to some extent.In order to obtain a more accurate pattern,a mathematical model based on the geometric structure of HXI is developed in this paper.The necessity of the new method can be demonstrated by an indepth analysis of the imaging technique.
Direct imaging and indirect imaging are two major techniques to observe the Sun in the hard X-ray band.But in terms of a hard X-ray observation instrument,direct imaging as that in the visible light band still faces many technological difficulties,although it has been developed for many years(Mi et al.2019).In contrast,Fourier-transform imaging,as a kind of typical indirect modulation imaging technique,has been applied to solar X-ray imaging observation and achieved fruitful results for several decades.The hard X-ray telescope(HXT)onboard the Yohkoh mission(Sakao 1994),the Reuven Ramaty High-Energy Solar Spectroscopic Imager (RHESSI)(Lin et al.2003),and the Spectrometer/Telescope for Imaging X-rays (STIX) onboard the Solar Orbiter mission (Krucker et al.2020) are three of the most well-known solar X-ray imaging instruments using such FT imaging technique.The new solar hard X-ray imaging instrument HXI also applies the FT imaging technique.
To study the imaging process of HXI,it is first necessary to state the imaging principle of FT-type telescopes.This kind of instrument contains several groups of bi-grid sub-collimators with different pitches,position angles,and phase angles.The differences of each sub-collimator can reflect the spatial information of the sources,which are called “modulation modes.” Each sub-collimator modulates the photon flux physically,and the detector right behind it records those photons that pass through the sub-collimator as a result of the modulation.By subtracting the particle background,results containing only the original information component can be obtained.The original image can be rebuilt by analyzing the modulation modes with their results.
The most popular ways to achieve image reconstruction are to go through its pattern or visibility.The pattern is formed by the angle-transmittance response,or called the modulation function of the corresponding sub-collimator,and the pattern isactually the final modulation function of the detector.The reconstructed images can then be obtained by solving the pattern matrix.Meanwhile,the visibility is formed by the counting of a pair of sine and cosine sub-collimator with the same modulation mode,each representing a two-dimensional Fourier component of the source.After that,further methods,like Clean,Pixons,and Forward-Fitting,can be used to form them into reconstructed images (Hurford et al.2003).Although the mathematical details of those methods are totally different,they all start with the analysis of the modulation function.It is worth noting that the effect on the image quality caused by observation errors during the modulation and reconstruction process is independent of the effect caused by using an inaccurate pattern,and the inaccurate pattern amplifies errors from observation.The modulation function serves as the basis of the entire reconstruction algorithm,a more precise pattern can lead to a better-reconstructed image.Therefore,it is beneficial to obtain knowledge about modulation functions as much as possible.
The modulation function of a sub-collimator presents a simple triangle waveform for the ideal instrument condition.However,the modulation function takes on a more complicated shape due to practical manufacturing techniques and environmental effects.Prince and Hurford mentioned a uniform way to analyze sub-collimators by convolving the two layers of the grid in their review (Prince et al.1988).They also pointed out that in many cases,despite being a triangle wave,the modulation function can be considered as a cosine function.This was also used in the HXT data progress(Kosugi et al.1991).Because the widths of the slits and slats of grids on RHESSI are unequal,the standard triangle wave could not be used.To improve the accuracy of the reconstruction,a Fourier cosine expansion was adapted as the modulation function (Hurford et al.2003).This method of Fourier cosine expansion was also applied in STIX to form its pattern (Benz et al.2012).
However,the precision of these methods is limited for a detailed analysis of actual engineering errors,such as machining tolerance,and deformation of the instrument.So,numerical simulation has been used as a complement to it,and the modulation function in special cases can be solved by performing Monte Carlo simulations.But anyway,this would take more time to perform the simulation works,especially under the condition that some parameters need to be changed within a certain range.Although the numerical method is more accurate,it is less resolvable and efficient.Consequently,since HXI has been implemented,there is an urgent need to develop a more detailed mathematical model of the collimator.During the assembly and launch of the satellite,the collimator might undergo some slight deformation.These deformations will have a considerable impact on the imaging reconstruction process,so each sub-collimator’s modulation function needs to be modified according to its deformation.Traditional methods of computing modulation functions are either inaccurate or unanalytical,but our accurate mathematical model can do better in terms of speed,accuracy,and analyticity,and will certainly facilitate the evaluation of HXI’s test and data process.
The new instrument HXI,as one of the payloads onboard the Advanced Space-based Solar Observatory (ASO-S),is an FTtype imaging telescope used to investigate the acceleration and transmission of electrons in the solar atmosphere during eruptions (Su et al.2019;Zhang et al.2019).ASO-S is China’s first comprehensive solar mission,launched on 2022 October 9.Aiming for the 25th solar maximum,it focuses on three major fields of solar activity: the photosphere magnetic field,coronal mass ejections (CMEs),and solar flares (Gan et al.2019).This satellite has been sent to a 720 km Sunsynchronous orbit and will have a lifetime of at least four years.HXI employs a spatial modulation technique that is similar to Yohkoh/HXT.Table 1 shows the configuration and characteristics of Yohkoh/HXT,RHESSI and SO/STIX in comparison to HXI.

Table 1 Comparisons of Several Missions with HXI
The rest of this paper is structured as follows:In Section 2,a new mathematical model for the transmission function of a collimator which is based on the geometric relationship is introduced the first step by step,and then put into a variety of complex conditions to see how it works.Next,a brief introduction to the structure of HXI is given in Section 3,followed by the simulation and experimental works done with the practical HXI collimator conditions in order to confirm the mathematical model.Then it comes to a discussion about how this model helps the data process in Section 4.Finally,Section 5 gives a summary and a brief outlook on this work.
2.Calculation of Modulation Functions
In this section,we start to build a detailed model for subcollimators.First,a simple case with only a sub-collimator in perfect condition is discussed.Next,the six degrees of freedom for a rigid body are calculated on this basis,and then the simplification of this model will be reported under some particular conditions.Finally,extended sources and unparalleled light are considered to match the X-ray beam test.This section contains a large number of symbolic operations,to make it clearer,a table explaining the various symbols can be found in the Appendix.
2.1.Basic Calculation
We need to work out the transmittance function for a single grid in this part.In the center of the grid,a coordinate system is built and the definition of the incidence angle of photons is specified (see Figure 1).Notice thatyand φ can be ignored when analyzing the grid because of the translational symmetry in itsydirection.Thus,the transmittance function can be written asT(x,θ),wherexis the photon’s incidence point and θ is its incidence angle.

Figure 1.In the definition of coordinate system and incident angles,notice that the point (0,0) is defined in the middle of a slat.The arrows mark their positive direction.
Here,this formula is applied to photons with an energyEto work outT(x,θ):
wheret(x,θ) is the length of tungsten that photons with incidence positionxand incidence angle θ pass through.λEis the photons’ radiation length in tungsten at energyE.Based on the geometric relationship,when θ ≪1,t(x,θ)can be written as:
Here,w(wire) is the width of the tungsten slat,sstands for the width of the slit,p=s+wis the pitch of the grid andufor the thickness of the grid.This equation only works whenwhich is met in most cases for a sub-collimator.So we haveT(x,θ) as:
Taking into account that the form of FT is favorable for integration works,forT(x,θ)is a periodic and even function,a Fourier cosine expansion can be performed toT(x,θ):
The modulation function of a 36 μm-pitch sub-collimator withs=20 μm,u=1000 μm,L=1190 mm,θ0=0,and a series summation ofn=20 is shown in Figure 2.It can be obtained that the DC component drops as the angle becomes larger,and the shape of the function changes near 0°.3 and 1°.3.It also shows that a summation of only 20 series can effectively handle the unequal of slit and slat.

Figure 2.The modulation function of a 36 μm-pitch sub-collimator with s=20 μm,u=1000 μm,L=1190 mm,θ0=0,and a series summation of n=20.The function from −1°.5 to 1°.5 is shown on the left with the blue line,while the orange line represents its DC component.The right shows the detail of the center of the left curve.
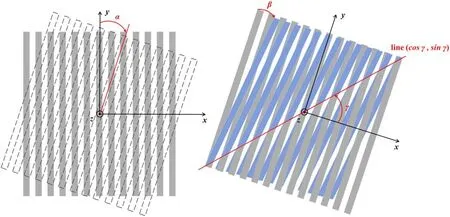
Figure 3.The definition of the rotations is described by rotation matrices A(left) and B(right).Here,α,β and γ can describe all the rotations in space.
2.2.Degrees of Freedom (DOFs): Rigid Body
The modulation function of an ideal sub-collimator has been discussed above.However,it will not be perfect since manufacturing errors and launching deformation in position and angle may occur.In this part,we consider the grid as a rigid body,calculate its movements in six DOFs to investigate their influence on modulation function,and then try to simplify it under several conditions.
2.2.1.Rotation Matrix of a Single Layer of Grid
A rotation matrix is defined for the grid to help with the analysis: First,the grid rotates clockwise by α degrees with itsz-axis(matrixA).Then it flips β degrees clockwise by a line on the grid’s plane (matrixB),the line has a counterclockwise angle γ from the grid’sx-axis (Figure 3).
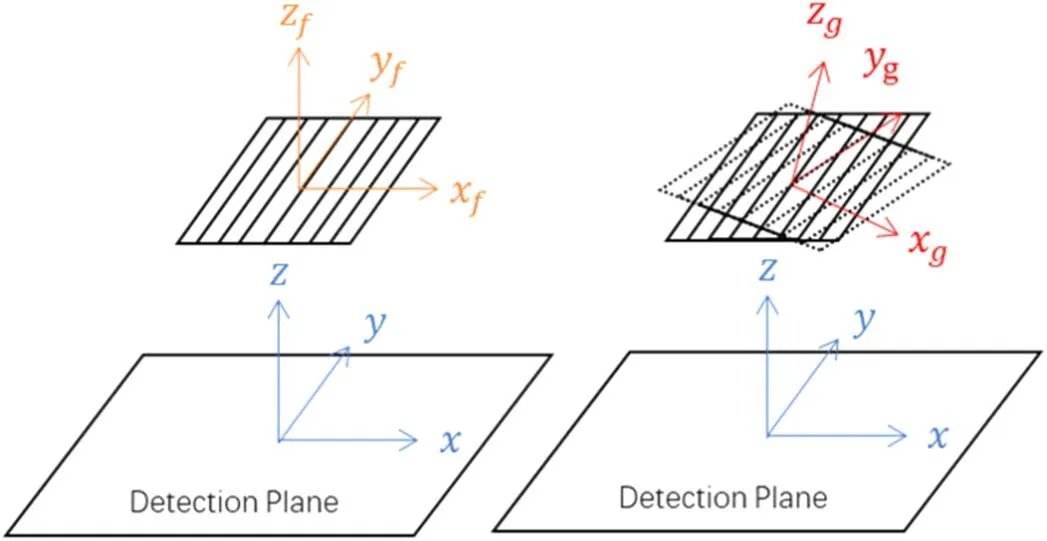
Figure 4.The three coordinate systems are defined:the“detection plane system”is fixed on the detector;the“system f”only moves with the grid and keeps parallel with the “detection plane system,” while the “system g” moves and also rotates with the grid.
The rotation matrix of the first rotating is matrixA:
Here we usecθto represent cosθandsθfor sinθ.The flip’s rotation matrix is matrix B:
So here,matrix S is the rotation matrix of the whole process:
Compared with the Euler matrixEunder (z,y,z′) system of Euler angles (a,b,c):
the relationship between(α,β,γ)and(a,b,c)can be found as:
Therefore,it is clear that the matrixSprovides a complete description of the three-dimension rotation.
2.2.2.The Projection of Incident Photon to the Detection Plane
We have already shown that incident photons with positionxand angle θ have a transmittance ofT(x,θ) in the previous section.Here,xand θ are defined in a coordinate system fixed to the grid,which we refer to as “coordinate systemg.” This system follows the movement and rotation of the grid.The subscript “g” will be used to describe parameters under this system,soT(x,θ) will be written asT(xg,θg).The “coordinate systemf,” which moves with the grid but does not rotate with it,is one of the coordinate systems defined.Parameters in it will be described using the subscript “f.” Another is the “detection plane system,” which is the coordinate system associated with the detection plane and in which we will finally give out the results of modulation functions.The definitions of these three systems are shown in Figure 4.

Figure 6.This scheme shows the placement of the ground X-ray beam instruments with the collimator and detector.

Figure 7.The definition of position and incident angle of non-parallel light and extended source.Here we assume that the small angle approximation is met.
Starting from here,due to the effect of rotation,we will describe the incident photon using four parameters (x,y,θ,φ)for calculation.Here,(x,y) describes the position where the photon hits theXOYplane of the coordinate system,and a vector (-t anθ,-t anφ,-1)defines the coming position of the photon.A vector (−θ,−φ,−1) is used to describe the photon in HXI because θ and φ are ≪1.On theXOYplane of thegsystem,it has:
Since we are calculatingT(x,y,θ,φ) under the detection plane system,the first step is to determineT(xf,yf,θf,φf).Here,from the systemftog,it has:
In the above formula,θgand φgare the functions of(θf,φf).By calculating the direction vector of the incident photon in systemsgandf,the relationship between them can be described as:
Here,S3is the third row ofS:S3=(sβsα−γ,sβcα−γ,cβ).Finally,we get:
Then,assuming that the translation offset of the grid is (x0,y0,z0),and the distance of the grid to the detection plane before the translation isLg,so it has:
After simplifying them,we can get:
They are the transformation from the detector’s coordinate system to the grid’s coordinate system we require.
2.2.3.Integration of Double Layer of Grids
Through the calculations above,T(x,y,θ,φ) can now be written as:
The termg0is inserted into the summation term to ease the statement and now the series is summed up from zero.To solve the modulation function of two layers of grids,we will substitute the subscriptgin the preceding equations witht(top)andb(bottom) to identify the function of the front plane from the rear plane:
The front grid has a set of parameters that are described by the subscriptt: (αt,βt,γt,x0t,y0t,z0t,Lt,st,wt,pt,ut),whereas the back grid’s parameters are described by the subscriptb:(αb,βb,γb,x0b,y0b,z0b,Lb,sb,wb,pb,ub).
Assuming that the detection area isD,the modulation function can be calculated as:
First,to consider a rectangle detection area of lengthwaand widthwb,the result is:
This result may have singular points in several values likeamn±=0 orbmn±=0,here their values are defined as limitations:
Then consider a round detection area with a radiusr:
Here,J1(x) is the Bessel-J function of the first order.Also,the values of singular points are defined as limitations:
2.2.4.Approximation Under Engineering Conditions
Here,it can be found that,for the samex,the higher the value ofn,the fasterFn(x)tends to 0.For the samen,the larger the value ofa,the fasterFn(ax) decreases to zero.Because of these,as long as the termFn(ax)exists,the series’higher-order terms tend to converge quickly.
We can keep simplifying the function if some further assumptions are made: When there is no incline angle,that is βt=βb=0,it has θb=θt=θg=θch−φsh.ThenP(θ,φ)can be simplified as:
2.3.Behavior Under Artificial X-Ray Sources
The behavior of the sub-collimator under artificial sources will be described in this section.To verify this model,the HXI needs to be characterized by an X-ray beam for its modulation functions.However,the parallel X-ray beam is quite difficult to get on the ground,so we normally produce the X-ray beam by hitting a molybdenum target with accelerated electrons,then limiting the beam’s divergence via pipe and diaphragms.So here,we will discuss an X-ray source with a launch area of a radiusrs,a pipe lengthl,and a diaphragm of a radiusRat the pipe’s end.As shown in Figure 6,the collimator is put on a rotatable platform so that the incident angle of the X-ray beam can be changed step by step during the test.
Consider the situation where there is only non-parallel light.The incident angles(θ,φ)for parallel light do not change with the incident position (x,y).However,with non-parallel light,assuming an incidence angle of (θ,φ) at the center (0,0),as shown in Figure 7,the incident angle of photons hitting point(x,y) will beThen we can have the integration:
In this integration,the high-frequency terms are ignored and superscript ′are used to indicate the terms that contain(θx,φy).Notice thathere is an integration of:
Apply the mean value theorem toP(θ,φ),and consider that in the experiment angles (θx,φy) are quite small,P(θ,φ) can be estimated as:
3.Simulations and Experiments for Collimator of HXI
The structure of HXI with its collimator is described in this part,followed by simulations using Geant4,a Monte Carlo simulation software for high-energy physics.Then we present the X-ray beam experiments with the results.To prove the mathematical model,all of these works are compared to the calculation results.
3.1.Structure of HXI
Figure 8 depicts the structure of HXI.It consists of three major parts: a collimator (HXI-C) performs physical Fourier transformation for incident photons,a spectrometer (HXI-S)detects the spectrum of transmitted photons,and an electronics control box(HXI-E)provides functions as a power supply,for payload control and data management (Zhang et al.2019).

Figure 8.The structure of HXI onboard ASO-S.

Figure 9.The structure of HXI-C.
The HXI-C (Figure 9),which modulates X-ray photons,is made up of two plates mounted on a titanium (Ti) framework.The plates have an array of 11×9,however,only 91 subcollimators are set for modulation.The rest of the eight holes are reserved for the measurement of the collimator’s pointing and particle background.The Solar Aspect System (SAS),which is mounted on the rear plate,assists in locating the Sun’s center and monitoring distortion between the front and rear plates (Chen et al.2021).
Each sub-collimator is comprised of two grids that are arranged in the same position as the front and rear plates,with a distance of 1190 mm between them.Different sub-collimators’grids have different pitches and rotation angles,allowing them to function as different u-v parameters in frequency space.The grids,which are made of tungsten foils,are held together by tungsten rings (see Figure 10).The rings set a limit on the effective area of grids,which is 36 mm in diameter for frontplate grids and 22 mm for rear-plate grids.The detectors assembled in HXI-S have a round detection area with a diameter of 25 mm.

Figure 10.The slit array of grids and its outer rings.A front grid with a 36 mm diameter is shown on the left,with a rear grid with a 22 mm diameter on the right.

Figure 11.The modulation functions of grids with p=36 μm, s=20 μm, L=35 mm, l=26 m, d=2rs=0.4 mm, D=2R=10 mm (left)/20 mm (right),α=β=0,θ0=0 and a series summation of n=2.The black points represent simulation results,while the blue line is the calculated curve.
3.2.Simulation of Modulation Function in Geant4
In this section,we will go over several Geant4 simulation results.We want to show that the mathematical model works effectively in solving near-ideal situations.
First,we look at a situation of 36 μm-pitch grids withp=36 μm,s=20 μm,L=35 mm,l=26 m,d=2rs=0.4 mm,α=β=0 and θ0=0.Here,the front grid of it is placed only 35 mm away from the rear grid,allowing us to see the change of the function with angle θ more clearly.Then we put it in the beaming tube to see how it behaves under experiments.It is worth noticing that the series in the modulation factor is not small enough to exclude high-order terms.As a result,we still need to compute the summary of the first two orders.We simulated it in Geant4,and the computation and simulation results are shown in Figure 11.All of the simulations below were run under 30 keV energy.
We can see that,in this case,the function cannot be represented as a simply cosine function,but must be treated as a summary of terms.After that,we apply the inclination to it,as shown in Figure 12.Compared to the functions without inclination in Figure 11,it can be found that the inclination effect lowers the function’s maximum value and brings a platform to it,and the length of the platform is the inclination angle β.
The twist angle α is then taken into account.We will look at the situation in parallel light,for twist angle will be one of the most affected parameters during launch.We want to evaluate how big of an impact it has on the modulation factorthose high-order terms decay quickly,so we simply considerWe can deduce from the form ofthat,for the same Δα,the smallerpis,the larger its effect would be.So,in Figure 13,we analyze a 36 μm-pitch sub-collimator on HXI and plot itsF1∼Δα curve.
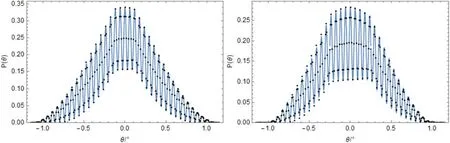
Figure 12.The modulation functions of grids with p=36 μm,s=20 μm,L=35 mm,l=26 m,d=2rs=0.4 mm,D=2R=20 mm,α=0,γ= ,β=15′(left)/30′(right).The black points represent simulation results,while the blue line is the calculated curve.

Figure 13. F1 ∼Δα curve for 36 μm-pitch sub-collimator with r=11 mm.
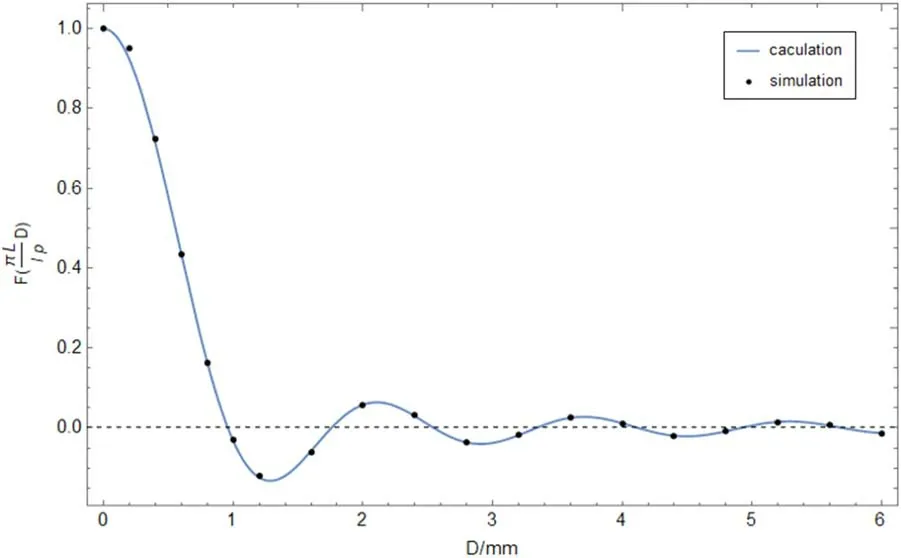
Figure 14.FunctionF1 ~D.Here, p=36 μm, l=26 m,and L=1190 mm.

Figure 15.The structure of the experimental devices.
It can be noticed from the curve that the first zero-point of the curve occurs at roughly 7′ for 36 μm-pitch grids.F1is around 0.96 for a 1′twist.As a result,we can conclude that its effect on the 36 μm-pitch can be ignored as long as the twist angle Δα is kept under 1′.
It can be seen from the above comparison of the math model with Geant4 results that the model works well when only considering the geometric relationship.However,in real-world situations,a variety of environmental factors may play a role in the outcome.To verify this model,more evidence from the experiment is needed.
3.3.Verification Tests of X-Ray Beam Experiments
The verification test of HXI was performed after determining the experimental parameters by simulation works.The experimental device’s structure is depicted in Figure 15.An X-ray source with an emitting area which is a disk of diameterd=2rs=0.4 mm was utilized in this experiment,and the electronic beam’s energy was turned to 30 keV.Photons travel the length of the tube,which isl=26 m.A diaphragm withD=2Rwas placed at the end of this tube to limit the angle distribution of photons.The size of the diaphragm could be adjusted as needed.A monitor was also assembled nearby to measure the intensity of the X-ray beam.The HXI-C and HXIS were mounted on a rotatable platform with high precision.The HXI was rotated to change the incident angle θgof photons in the experiment.

Figure 16.The curve ofF1 ~D for a 224 μm-pitch sub-collimator with L=1190 mm and l=26 m.The value from the math model is shown by the blue line,while the black points represent the results of the experiment.The top right diagram depicts the measurement region in this experiment.

Figure 17.The calculation curve of 344 μm-pitch sub-collimator with s=172 μm,u=2000 μm,D=9.1 mm,d=0.4 mm,L=1190 mm,l=26 m,and a rotation angle α=31°.The diameter of the front grid is 36 mm,22 mm for the rear grid,and 25 mm for the detector.The curve is a contour of modulation components.
The platform could only be rotated horizontally during the experiment due to the platform’s design.As a result,θgbecomes a function of the platform’s rotation angle θpand rotation angle α:θg=θpcosα.So,the modulation functionP(θp) on rotation angle θpcan approximately be written as:
Here,D=2R,d=2rs.Then it came to the measure of the“factor of the diagram.” A 224 μm-pitch sub-collimator was used in this experiment.We first found out the function’s peak area to ensure that photons can nearly incident normally.The diaphragm was then changed in size,and the platform was rotated for each diagram to measure the peak and valley of the modulation.After a series of analyses,we were able to obtain the curve for the “factor of the diagram,” which is shown in Figure 16.
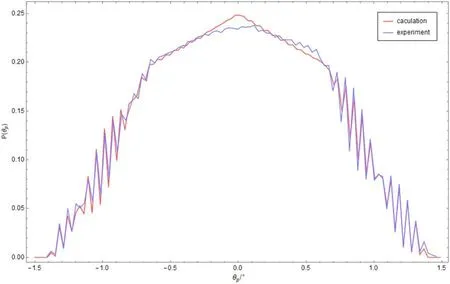
Figure 18.The computed result of the “DC” curve (red) compared to the experiment result (blue) with the same sampling frequency.
After that came the measurement of the DC component for the modulation function.Considering the form of the function,if a suitable size for the diaphragm was chosen to makethe pure DC component could be obtained from the experiment.But notice that,in the experiment,the incident angle was changed by rotating the platform.Therefore,when the angle is large,the front plane or the real plane might shadow the detector.Under these situations,the effect of occluding might make the detection zoom far away from a round area.So,the result of the integration on the round area did not work this time,and the shape of the detection area even changed with the rotation of the platform.We solved the integration by applying a changeable area with the angle,and the result can be seen in Figure 17.In this figure,the calculated curve of a 344 μm-pitch sub-collimator is shown with a rotation angle α=31°.It can be seen that no occlude effect works from −0°.6 to 0°.6 where the integration area is round andIt means that the curve shows the DC component.As the rotation angle becomes larger,occlude effect occurs,so the shape of the function starts to change.The integration of the non-circular area and the amplitude of the original AC component jointly contribute to the final amplitude.
The modulation components in the diagram change at a really high frequency.Due to the time limit,it was unable to attain such a high sample frequency in the experiment.The measured curve will be limited by the contour of Figure 17 if the sampling frequency is not high enough.Figure 18 shows the contrast between the calculated and experimental results.The calculation and experiment were both done with the same sampling frequency.These two experiments strongly show that our math model works effectively even under complex conditions.
4.Discussion: Data Process with the Model
In this section,it is discussed how to consider the effects of the deformation of HXI-C in the data process,and to what extent they may affect the modulation function.These results will present the application of the model and its superiority over other methods in calculating the pattern.
To correct the instrument deformation,the first step is to monitor the state of HXI-C with the Displacement Monitor(DM)after it is launched into space (Zhang et al.2019).It can measure the twists and shifts between the front and rear plates,so the deviations in position and angle for each sub-collimator can be calculated.Then the modulation function for each bigrid can be figured out,considering all its deformations.As a result,the effect of the deformation of HXI-C in the image reconstruction process could be weakened as much as possible by using the new modulation functions.Notice that in Section 2.2.4,an assumption of those deformation angles always satisfying small angle approximation has been mentioned.Zhang’s article mentioned above has shown that during the whole mission of the satellite,all the deformation angles could be controlled within several arcseconds,and this has been verified through environmental tests.However,as long as those angles are kept below 1°,they are still satisfied with the small angle approximation.So,the simplifications in Section 2.2.4 can work during the whole life of ASO-S,since there is a huge gap between error control and assumption failure.
To show how this model works,here we suppose that the imaging area lies near the edge of the Sun,while HXI-C points to the center of the Sun.Under this condition,the thickness of the grids is the item that affects most.To see its effect more clearly,we approximate the DC component of the modulation function when the energy is not high:here we apply the assumption of λ ≪u.As shown with the yellow curve in Figure 2,the DC component drops as the incident angle becomes large.Since the term∣θ∣appears in the formula,this effect is more pronounced for grids with larger thickness and smaller pitch.

Figure 19.The reconstructed images of the test sources.The left one gives the ideal result as a reference,the middle one is done without considering the effect of thickness,while the right one is considered.

Figure 20.In the reconstructed images of the test sources,the left one gives the ideal result as a reference,the middle one is done without considering the effect of twist,while the right one is considered.
As a test,in Figure 19,two point sources are placed at the edge of the Sun to see how this model helps to improve the results.The chosen area is the upper left edge of the Sun,15′away from its center.The two-point sources—one is twice brighter than the other—are placed at a distance of 1.5×resolution,with an energy of 30 keV.The counts for each subcollimator are calculated,then the image is reconstructed without and with the consideration of the thickness effect.Notice that in the reconstruction process,for grids with different position angles,the incident angle θ from the same source can be different.Therefore,each pattern needs to be calculated and corrected separately and then recombined to form the final image.It can be clearly seen that the shape and the brightness of the sources go wrong if the thickness of the grids is not calculated.
Then it comes to the affection of twist angle Δα.As mentioned in Section 2.2.4,this effect contributes as a modulation factorSo,as a function ofΔαshown in Figure 13,for the same twist angle Δα,its impact becomes bigger as the pitch of the grid goes smaller.As Figure 13 shows,for the grid with the smallest 36 μm-pitch in HXI,as long as the twist angle is smaller than 1′,its effect on the modulation can be ignored.If the twist angle is larger than that,the modulation function needs to be corrected.In Figure 20,the same sources are used as in Figure 19,but this time they are placed in the center of the Sun.A twist angleΔα=2.′5 is added to the instrument,and it can be seen that the twist makes the sources darker,but does not change the shape.

Figure 21.The reconstructed images of the test sources,the left one gives the ideal result as a reference,the middle one is done without considering the effect of thickness and twist,while the right one is considered.
For the effect of inclination,as Figure 12 shows,it brings a platform that has a length of the incline angle β to the center of the modulation function.The incident angles θtand θbare the terms that consist of the incline angle β,and the DC componentg0(θt)g0(θb)is the most affected part,especially when θtand θbare of the same order of magnitude as β.As a result,the effect of inclination mainly occurs when the incident angle is close to zero.This affection mainly reduces the DC component of the modulation function,and it can be solved just like the effect of thickness.
Then,the case in which different types of effects are combined would be discussed.As shown in Section 2.2.4,the modulation function under engineering conditions has a form of
In this expression,the termsg0(θt)g0(θb)andgn(θt)gn(θb)are affected both by thickness and inclination.Fortunately,they can be distinguished more finely:g0(θ) andgn(θt) are only affected by thickness,while θtand θbare only affected by inclination.The effect of twist,which only appears in the termcan be easily corrected.So,both effects can be modified independently.To visualize this process,a case combining both effects in Figures 19 and 20 is discussed.The sources are placed at the edge of the Sun,while a twist angle Δα=2.′ 5is added to the instrument.Figure 21 shows the comparison before and after the corrections,it can be found that sources without corrections are darker than that in Figure 19.Since the effect of thickness and inclination are independent of each other,we can correct them in any order:If the effect of thickness is corrected first,we will get the image in Figure 20,then the twist of the instrument is corrected to get the final picture.Otherwise,the image in Figure 19 will be first obtained if the effect of the twist is corrected first.These corrections could be made at the same time and this will not make any difference to the final result.
In these cases above,although the traditional method of numerical simulation can do the same job in revising these effects,applying the new model can be much faster.More importantly,this model,which can give out the mathematical form of those deformations,is much better in analyticity.
5.Summary
In this paper,a new mathematical model for HXI by digging into the structure of the FT imaging telescope is given.This model is formed by analyzing the geometric structure of the sub-collimator,with different types of deformation taken into consideration.The modulation functions under various conditions are calculated,and Monte Carlo simulations are performed to confirm the accuracy of the calculations.A series of experiments are also designed to test this model,and the model can match the experiment results really well.The ability of this model in solving patterns under different types of deformation is also shown.Notice that this model is not only sufficient in analyzing the image reconstruction process of HXI,but also quite useful with other telescopes as long as they use a similar imaging theory as HXI.On the other hand,we can use this model to analyze the deformation of HXI and its influences on imaging ability after launch.By correcting the deformations,a more accurate pattern will be provided to the imaging reconstruction process;we believe that it will be much beneficial in observing solar flares.
Acknowledgments
This work is supported by the Strategic Priority Research Program on Space Science,Chinese Academy of Sciences(No.XDA 15320104),the Scientific Instrument Developing Project of the Chinese Academy of Sciences (Grant No.YJKYYQ 20200077),the National Natural Science Foundation of China(Nos.12173100,12022302,11803093 and 11973097),and the Youth Innovation Promotion Association,CAS (No.2021317 and Y2021087).The worthful work during X-ray beam experiments carried out by the HXI group is also appreciated.
Appendix Symbol Explanation
A list of symbols used in this paper has been summarized in Table A1 for quick reference.

Table A1 Symbols Used in This Paper
ORCID iDs
杂志排行
Research in Astronomy and Astrophysics的其它文章
- Application of a Magnetic-field-induced Transition in Fe X to Solar and Stellar Coronal Magnetic Field Measurements
- Simulation-driven Wind Load Analysis and Prediction for Large Steerable Radio Telescopes
- Gravitational Wave Radiation from Newborn Accreting Magnetars
- Power-law Distribution and Scale-invariant Structure from the First CHIME/FRB Fast Radio Burst Catalog
- Solar Active Region Magnetogram Generation by Attention Generative Adversarial Networks
- The Decay Process of an α-configuration Sunspot
