Gravitational Wave Radiation from Newborn Accreting Magnetars
2023-03-25QuanChengXiaoPingZhengXiLongFanandXiHuang
Quan Cheng ,Xiao-Ping Zheng ,Xi-Long Fan ,and Xi Huang
1 Institute of Astrophysics,Central China Normal University,Wuhan 430079,China;qcheng@mail.ccnu.edu.cn,zhxp@mail.ccnu.edu.cn
2 School of Physics and Technology,Wuhan University,Wuhan 430072,China
3 School of Mathematical and Physical Sciences,Wuhan Textile University,Wuhan 430200,China
Abstract The observed electromagnetic radiation from some long and short gamma-ray bursts,and neutron stars(NSs),and the theoretical models proposed to interpret these observations together point to a very interesting but confusing problem,namely,whether fall-back accretion could lead to dipole field decay of newborn NSs.In this paper,we investigate the gravitational wave (GW) radiation of newborn magnetars with a fall-back disk formed in both the core-collapse of massive stars and the merger of binary NSs.We make a comparison of the results obtained with and without fall-back accretion-induced dipole-field decay (FADD) involved.Depending on the fall-back parameters,initial parameters of newborn magnetars,and models used to describe FADD,FADD may indeed occur in newborn magnetars.Because of the low dipole fields caused by FADD,the newborn magnetars will be spun up to higher frequencies and have larger masses in comparison with the non-decay cases.Thus the GW radiation of newborn accreting magnetars would be remarkably enhanced.We propose that observation of GW signals from newborn magnetars using future GW detectors may help to reveal whether FADD could occur in newborn accreting magnetars.Our model is also applied to the discussion of the remnant of GW170817.From the post-merger GW searching results of Advanced LIGO and Advanced Virgo we cannot confirm the remnant is a low-dipole-field long-lived NS.Future detection of GWs from GW170817-like events using more sensitive detectors may help to clarify the FADD puzzle.
Key words: stars: neutron–stars: magnetars–stars: magnetic field–gravitational waves
1.Introduction
Newborn millisecond rotating magnetars are generally proposed to be the central engines of some long gamma-ray bursts (LGRBs) (Dai &Lu 1998;Zhang &Mészáros 2001;Thompson et al.2004;Metzger et al.2011),short gamma-ray bursts (SGRBs) (Fan &Xu 2006;Metzger et al.2008;Rowlinson et al.2013),superluminous supernovae (Kasen &Bildsten 2010;Woosley 2010),bright mergernovae (Yu et al.2013),rapidly evolving and luminous transients (Yu et al.2015b),and fast radio bursts(Ravi&Lasky 2014;Zhang 2014;Metzger et al.2017).These magnetars are also promising targets for gravitational wave (GW) searches using the Advanced LIGO (aLIGO),Advanced Virgo (aVirgo),and future Einstein Telescope (ET) due to their strong magnetic fields and fast rotations (Dall’Osso et al.2009;Sathyaprakash&Schutz 2009;Cheng et al.2017).
Various of physical mechanisms in newborn magnetars could produce GW radiation,for instance,the dynamical barmode instability (Lai &Shapiro 1995),secular instability (Lai&Shapiro 1995),f-mode instability (Andersson &Kokkotas 1996),r-mode instability (Andersson 1998;Owen et al.1998),stellar radial oscillations(Dai 2019),and magnetically induced quadrupole deformation (Stella et al.2005).Among them,the GW radiation from magnetic deformation of newborn magnetars may not only be relatively strong (compared to the r-mode instability) but also cover a relatively wide frequency range(compared to the bar-mode instability,secular instability,f-mode instability,and radial oscillations) that could possibly extend to the sensitive bands of aLIGO,aVirgo and ET(Fan et al.2013;Cheng et al.2015;Dall’Osso et al.2015;Glampedakis &Gualtieri 2018).The GW radiation from magnetic deformation of a newborn magnetar critically depends on both the ellipticity and evolution of the magnetar.
The ellipticity of magnetic deformation of a neutron star(NS)has been extensively investigated(e.g.,Bonazzola&Gourgoulhon 1996;Cutler 2002;Stella et al.2005;Haskell et al.2008;Ciolfi et al.2009;Mastrano et al.2011,2015;Akgün et al.2013;Dall’Osso et al.2015).Previous results show that the ellipticity is mainly dependent on the internal magnetic energy,the internal magnetic field configuration,and the equation of state(EOS)of the NS (Haskell et al.2008;Dall’Osso et al.2015).While different NS EOSs could affect the ellipticity by only a factor of a few(e.g.,Ciolfi et al.2010;Mastrano et al.2011),the internal field configuration and internal magnetic energy(the strengths of the internal magnetic fields) crucially determine the sign (the shape of the deformed NS) and magnitude of the ellipticity,respectively.Magnetohydrodynamic (MHD) simulations suggest that in NSs the internal fields possibly have a poloidaltoroidal twisted torus configuration(Braithwaite&Spruit 2004,2006) with the toroidal fields playing a dominant role(Braithwaite 2009;Akgün et al.2013).This may be the case for magnetars,as observations of the X-ray afterglows of some LGRBs(Lü et al.2019a)and SGRBs(Gao et al.2016;Lasky&Glampedakis 2016),the giant flare of SGR 1806-20(Stella et al.2005),and the phase modulation in the X-ray pulsation of magnetar 4U 0142+61(Makishima et al.2014)all suggest that magnetars could have a strong internal toroidal magnetic field of∼1016G or higher and a dipole magnetic field that is a few times to about two orders of magnitude lower that the toroidal component (Cheng et al.2018).Theoretically,for magnetars born in the core collapse of massive stars or mergers of binary NSs (BNSs),their strong magnetic fields could be produced during the extremely early evolution stages of the remanent NSs due to the α–ω dynamo(Duncan&Thompson 1992),magnetic flux conservation (Ferrario &Wickramasinghe 2006),r-mode and Taylor instabilities (Cheng &Yu 2014),Kelvin–Helmholtz instability (Price &Rosswog 2006),and magnetorotational instability (Akiyama et al.2003;Duez et al.2006) (see Cheng et al.2018 for some detailed discussions).In the toroidaldominated scenario,a deformed newborn magnetar has a prolate shape whose ellipticity is,where,R,andMgare the volume-averaged strength of the toroidal field,radius,and gravitational mass of the magnetar,respectively.
As generally considered,when the differential rotation and amplification of the initial seed magnetic field end,the uniformly rotating newborn magnetar will spin down via magnetic dipole (MD) and GW radiation in isolation (e.g.,Shapiro &Teukolsky 1983;Zhang &Mészáros 2001;Gao et al.2016;Cheng et al.2017;Ai et al.2018).However,for the newborn magnetar produced in the core collapse of a massive star or merger of a BNS,it may not be isolated actually.Instead,the magnetar could be surrounded by a fall-back disk,which was formed due to fall-back of the bound matter ejected during the collapse or merger (see Metzger et al.2018 and references therein).
The presence of a fall-back disk may complicate the evolution of the newborn magnetar,thus further affecting its GW radiation.Some previous studies have only focused on the effect of fall-back accretion on the magnetar’s spin evolution(Bernardini et al.2013;Gompertz et al.2014;Gibson et al.2017),while others considered a more realistic case with its effect on the gravitational mass evolution involved simultaneously(Piro&Ott 2011;Dai&Liu 2012;Wang&Dai 2017;Metzger et al.2018).Depending on the values of the corotation radiusRc,magnetospheric radiusRm,and light cylinder radiusRl,the fall-back disk may exert a spin-up torque (the accretion phase),or a spin-down torque (the propeller phase),or even no torque(the ejector phase)on the newborn magnetar.Thus if the magnetar is expected to experience the accretion phase and/or propeller phase during its early evolution(Piro&Ott 2011;Dai&Liu 2012),its spin evolution and GW radiation will differ from that of an isolated magnetar with the same physical parameters.Moreover,the gravitational mass of the newborn magnetar will increase in the accretion phase.The fate of the magnetar is dependent on its initial mass,the amount of matter accreted,and the NS EOS.The magnetar will collapse to a black hole (BH) with its GW radiation being terminated abruptly,if its gravitational mass surpasses the maximum gravitational mass that the uniformly rotating NS can sustain(Lasky et al.2014;Gao et al.2016;Li et al.2016;Cheng et al.2017).Otherwise,the magnetar will be long-lived and produce a long-lasting GW signal (Lasky et al.2014;Gao et al.2016).
It is also possible that fall-back accretion may lead to decay of the surface dipole magnetic field of the newborn magnetar,as the dipole field would be buried into the NS crust by the accreted matter (Muslimov &Page 1995;Geppert et al.1999;Shabaltas &Lai 2012;Bernal et al.2013;Torres-Forné et al.2016;Fraija et al.2018).The field burial scenario has been invoked to explain the low dipole magnetic fields of central compact objects (CCOs) in supernova remnants (Shabaltas &Lai 2012;Bernal et al.2013;Torres-Forné et al.2016;Fraija et al.2018)and NSs in X-ray binaries(XRBs)(e.g.,Shibazaki et al.1989;Melatos &Phinney 2001;Payne &Melatos 2004;Zhang &Kojima 2006;Priymak et al.2011;Haskell et al.2015;Mukherjee 2017;Suvorov &Melatos 2019),though the accretion rates in the two cases differ remarkably.Interestingly,the observed multiband electromagnetic(EM)counterparts(the kilonova AT2017gfo and the candidate X-ray flare detected at 155 days after the merger) of the first BNS merger event detected,GW170817(Abbott et al.2017a;2017b),indicate that the merger remnant is probably a long-lived massive NS with strong toroidal field and weak dipole field(Li et al.2018;Geng et al.2018;Yu et al.2018;Piro et al.2019;Lü et al.2019b),which may be simply the result of field burial caused by fallback accretion (Yu et al.2018).
Nevertheless,for newborn magnetars,the claim of fall-back accretion-induced dipole-field decay(FADD)seems to confront enormous challenges,as fitting of the significant brightening in early X-ray afterglows of some LGRBs (Dai &Liu 2012),the remarkable rebrightening in the late-time optical afterglow of GRB 100 814A (Yu et al.2015a),and the hump-like extended emission of some SGRBs (Gompertz et al.2014;Gibson et al.2017) all require that the dipole fields of newborn magnetars should keep unchanged when accretion proceeds.In theory,amplification of the dipole field of a newborn NS is possible during accretion and thus the burial effect may be weakened if the accreting matter is magnetized and/or if the thermoelectric instability arises in the stellar interior because of the existence of a large temperature gradient in such a newborn NS (Geppert 2009).However,it is also suggested that the accreting matter may not be magnetized since it has undergone a turbulent episode (Geppert 2009).Instead,the accreting matter may behave as a diamagnetic shield,which can profoundly reduce the strength of the dipole field (Bisnovatyi-Kogan &Komberg 1974;Geppert 2009;Mastrano &Melatos 2012).As an alternative dynamo mechanism,previous work has shown that for newborn rapidly rotating NSs without solid crusts,their dipole and toroidal fields can be quickly amplified to magnetar level due to r-mode and Taylor instabilities(Cheng&Yu 2014).Accretion can provide additional angular momentum to newborn NSs and thus facilitate the occurrence of r-mode instability and amplification of magnetic fields.Therefore,whether or not accretion would lead to dipole field decay of newborn NSs possibly depends on whether their solid crusts could have formed when accretion proceeds.In other words,FADD is expected to occur only when solid crusts are present.Unfortunately,the specific formation time of crusts is largely unknown because the cooling behavior of newborn NSs is rather difficult to be determined both theoretically and observationally.It is thus unable to conclude whether FADD is relevant for newborn magnetars.Nonetheless,it is still interesting to investigate the differences of the evolution behavior and GW radiation between the newborn magnetar with a constant dipole field and that with a decaying dipole field caused by fall-back accretion.
In principal,compared to the non-decay case,Rmof the newborn magnetar with a decaying dipole field should be smaller.Hence,if the magnetar entered the accretion phase(Rm In this paper,we make a comparison of the GW radiation from newborn accreting magnetars with and without FADD considered.We suggest that future detection of GWs from newborn accreting magnetars may help to answer whether FADD is relevant for these magnetars.If the merger remnant of GW170817 is a massive NS whose dipole field has decayed significantly after its birth due to fall-back accretion (Yu et al.2018),we also study the evolution and GW radiation of the remnant NS and compare our results to the upper limits of postmerger GW signals set by aLIGO and aVirgo.We note that FADD is also taken into account in Li et al.(2021) and Sur&Haskell (2021) when studying the evolution of a newborn magnetar with a fall-back disk and the associated GW radiation,however,they adopted a simple form to describe FADD,which may be inadequate. The paper is organized as follows.In Section 2,we introduce the spin and gravitational mass evolutions of newborn accreting magnetars and their magnetically induced GW radiation.The phenomenological models adopted to describe FADD are presented in Section 3.For the core-collapse and the merger cases,in Section 4,we respectively calculate the GW radiation from newborn accreting magnetars with FADD involved,and compare the results to those obtained by assuming a constant dipole field.We apply our model to the putative massive NS remnant of GW170817 in Section 5.We give conclusion and some discussions in the final section. After the core collapse of a massive star or the merger of a BNS,a newborn magnetar may be left and a fraction of the matter from the progenitor star or BNS is possibly bound to the central magnetar.The bound matter would fall back and subsequently circularize into an accretion disk around the magnetar.4In fact,for BNS mergers,the fall-back matter may form a torus in the innermost region around the central magnetar,and a disk surrounding the torus(Metzger et al.2018).In this paper,we treat them overall as a disk for simplicity.The mass of the fall-back matter and fall-back timescale in the core-collapse case are rather different from those in the merger case.A detailed description of the fall-back models in the two cases can be found in Metzger et al.(2018).Here,we briefly summarize their fall-back models.For the core-collapse case,the mass of the fall-back matterMfbis dependent on the energy,mechanism,and asymmetry of the supernova explosion (Metzger et al.2018).The characteristic fall-back timescaletfbis determined by the mean density of the progenitor’s shell that falls back after the explosion (Metzger et al.2018).However,for the merger case,Mfbandtfb,respectively,depend on the properties of the BNS system and viscous timescale of the disk(Metzger et al.2018).The specific values forMfbandtfbin the two cases should be given by numerical simulations.For simplicity,we here fixMfb=0.8M⊙andtfb=1000 s for the core-collapse case (Metzger et al.2018).An even larger valueMfb∼1M⊙may also be possible in this case(Perna et al.2014),however,it may lead to prompt collapse of the newborn magnetar,depending on the magnetar’s maximum sustainable gravitational mass.While in the merger case,we adoptMfb=0.1M⊙andtfb=0.1 s,and in order to see howMfbcan affect our results,an alternative valueMfb=0.01M⊙is also taken (Metzger et al.2018).The fall-back rate can be related toMfbandtfbas (Metzger et al.2018) This prescription for the fall-back rate can be applied to the two cases mentioned above.Hereinafter,we assume that the newborn magnetar accretes at a rate comparable to the fall-back rate (Piro &Ott 2011;Dai &Liu 2012;Ma et al.2018). With the presence of a fall-back disk,the spin evolution of the newborn magnetar can be given by where Ω andI=0.35MgR2are the angular velocity and moment of inertia of the magnetar (Lattimer &Prakash 2001),respectively.Ndip=−μ2Ω3/(6c3) is the torque from MD radiation,where μ=BdR3is the magnetic dipole moment withBdrepresenting the surface dipole magnetic field at the pole.is the torque due to magnetically induced GW radiation,andNaccis the torque exerted by the accretion disk.Before showing the specific form ofNacc,we would like to introduce three important radii,i.e.,Rm,Rc,andRl,which,respectively,have the following forms (Piro &Ott 2011): wheren(ω)=1 −ω is the dimensionless torque withrepresenting the fastness parameter,andis the Keplerian angular velocity withρ¯denoting the average density of the magnetar (Owen et al.1998).We can see that the fall-back disk can exert a spin-up torque on the magnetar ifRm On the other hand,fall-back accretion can also lead to the increase of the newborn magnetar’s baryonic mass if it is in the accretion phase.The evolution of the magnetar’s baryonic mass can therefore be determined as whereMb,iis the magnetar’s initial baryonic mass.However,if the magnetar is in the propeller or ejector phase,its baryonic mass will keep unchanged since no matter can be accreted onto it.For the magnetar with a baryonic massMb,its corresponding gravitational mass is (Dai &Liu 2012) Here the radiusRof the magnetar is assumed to be constant since it may only change slightly as the magnetar evolves(Dai&Liu 2012). With the evolution of the accreting magnetar,depending on the maximum sustainable gravitational massMg,maxof this uniformly rotating magnetar,it will be an eternally stable massive magnetar ifMg≤Mg,maxis always satisfied during the whole evolution.Otherwise,it will be a temporarily stable supermassive magnetar and collapse to a BH when the conditionMg>Mg,maxis fulfilled.Following Lasky et al.(2014),Mg,maxis NS EOS dependent and can be expressed as a function of the spin periodPof the magnetar as whereMTOVrepresents the maximum gravitational mass of a non-rotating NS,and α and β are EOS dependent fitting parameters.We first take the NS EOS GM1 (Glendenning &Moszkowski 1991) as a example.When discussing the GW radiation from the putative NS remnant of GW170817,another dense matter EOS,namely EOS DDME2 (see Ai et al.2020 and references therein) is also adopted for a comparison.For EOS GM1,the corresponding values forMTOV,α,and β are respectivelyMTOV=2.37M⊙,α=1.58×10−10,and β=−2.84 (Lasky et al.2014;Ai et al.2018).As a result,for this EOS,the range for the maximum sustainable gravitational mass is2.37M⊙≤Mg,max≤2.60M⊙.The lower limit is obtained by settingP=0 in Equation (9),while the upper limit is derived by settingP=PK=2π/ΩKforMTOV=2.37M⊙.As a contrast,for EOS DDME2,we haveMTOV=2.48M⊙,α=1.966×10−10,and β=−2.84(Ai et al.2018).Therefore,following the same method,the range forMg,maxis derived to be2.48M⊙≤Mg,max≤2.80M⊙for this EOS.Obviously,for EOSs that yield larger(smaller)MTOV,the newborn magnetar should be more liable to survive (collapse).From Equation (9),we can obtain the collapse frequency,below which the magnetar withMg=Mg,maxwill collapse(Cheng et al.2017).As we are only interested in eternally stable and temporarily stable newborn magnetars that can produce long-duration GW radiation,their collapse frequencies are infinitely small and within the range 0<νc<νi,respectively,where νiare the initial spin frequencies of the magnetars (Cheng et al.2017). To assess whether the dynamical bar-mode instability and secular instability could arise during the evolution of the magnetar and lead to additional GW radiation,we also estimate the ratio of the magnetar’s rotational energy to the absolute value of its gravitational energy,where ∣Eg∣can be written as (Lattimer &Prakash 2001) The dynamical bar-mode instability will occur for ζ>0.27(Lai&Shapiro 1995),while for the secular instability,the threshold is ζ>0.14 (Lai &Shapiro 1995). The GW from magnetic deformation of the newborn magnetar is emitted at a frequency νe=2ν=Ω/π and has a characteristic amplitude (Corsi &Mészáros 2009) where ν is the magnetar’s spin frequency anddthe distance to the magnetar.Hereinafter,except for the putative NS remnant of GW170817 which has a distanced=40 Mpc (Abbott et al.2017a;Cantiello et al.2018),we setd=100 Mpc when calculating the GWs from newborn magnetars.To roughly assess the strength of the GW signal,its characteristic amplitudehc(νe)is usually compared with the rms strain noisesof the detectors,whereSh(νe)is the noise power spectral density of a detector.For LIGO,Virgo,aLIGO and ET at their design sensitivities,the analytical formulas for the noise curvesSh(νe) are presented in Sathyaprakash &Schutz (2009).We have discussed the evolution of the newborn accreting magnetar with a constant dipole field and the associated GW radiation.In the next section,we will show two phenomenological models adopted to describe FADD. The fall-back matter accreted onto a newborn NS may also result in the decrease of the NS’s dipole magnetic field by burying it into the stellar crust (Muslimov &Page 1995;Geppert et al.1999).The burial processes of dipole field have been investigated through MHD simulations of fall-back accretion onto NSs produced in core-collapse supernovae(e.g.,Bernal et al.2013;Torres-Forné et al.2016;Fraija et al.2018).The results show that the accretion rate plays a crucial role in determining whether the dipole field of a newborn NS could be completely submerged into the crust(Bernal et al.2013;Torres-Forné et al.2016).Specifically,Bernal et al.(2013) found that a critical accretion rateis required to completely submerge the 1012G surface field.Moreover,assuming that accretion proceeds at a constant rate and lasts for 1000 s,Torres-Forné et al.(2016) derived a formula for the accreted mass ΔMrequired to completely submerge an initial surface fieldBd,i,which can be expressed as Thus the corresponding critical accretion rate for complete submergence isSince in Torres-Forné et al.(2016) the maximum accreted mass is limited to ΔM=1M⊙,beyond which the 1.4M⊙newborn NS may collapse to a BH,one can obtain the maximum initial field that could be buried asBd,i≈2.5×1014G and In fact,for both the core-collapse and the merger cases,depending onMfbandtfb,the accretion rate may satisfyat a certain stage.Therefore,ifdetermines whether the newborn NS’s dipole field could be buried,we speculate that a higherBd,i>2.5×1014G may be buried by stronger fall-back accretion with a rate,though detailed numerical simulations of fall-back accretion onto newborn millisecond magnetars and subsequent submergence of the dipole magnetic fields are needed to verify this conjecture.5One caveat is that mentioned above are calculated for newborn NSs with either a normal magnetic field (Bernal et al.2013) or a slow rotation(Torres-Forné et al.2016).For newborn magnetars of interest here, probably has a different form and should be determined via detailed simulations.Without accurate simulation results,we simply take the following assumptions:(i) the expression for the critical accretion ratecould be extrapolated toBd,i≈1015G;(ii) forandRc>Rm,6The latter requirement ensures the fall-back matter can be accreted onto the magnetar.the initial dipole field would be completely buried immediately(Bernal et al.2013),otherwise we consider no submergence would occur;(iii)if complete submergence occurred,the dipole field may reach the minimum strengthBd≈10−4Bd,idue to ohmic diffusion (Vigelius &Melatos 2009;Haskell et al.2015),as obtained for the dipole field of NSs in XRBs in the case of maximum submergence.This represents the first phenomenological model (hereinafter referred to as Model I) we use to describe FADD,in whichplays a critical role. The second phenomenological model (Model II) is accreted mass-dominated,which is established by analogy to the case of NSs in XRBs.The dipole field of these NSs could have been buried by the accreted matter from their companion,and its evolution can be expressed by a simple empirical formula(Shibazaki et al.1989;Zhang &Kojima 2006) where ΔMandMcare the mass accreted onto the NS and the critical accreted mass that determines the field decay rate,respectively.Originally,Mcwas proposed to be a constant in the range ∼10−5–10−4M⊙(Shibazaki et al.1989).Later,MHD simulations of field burial of accreting NSs in XRBs showed thatMcdepends on both the crust EOS and the initial field strength,and has a formfor some more realistic crust EOSs (Priymak et al.2011;Haskell et al.2015).Moreover,according to the simulation results,the empirical formula proposed by Shibazaki et al.1989)is valid only for ΔM After taking initial values for the physical quantities of a newborn magnetar,we can calculate its evolution and the GW signal.In both the core-collapse and the merger cases,the magnetars are assumed to be born with a dipole fieldBd,i=1015G and a toroidal fieldG initially,which are consistent with observations and simulation results(e.g.,Cheng et al.2018;Ciolfi et al.2019).The initial baryonic massesMb,iand angular velocities Ωiof newborn magnetars are difficult to be determined.Generally,the magnetars born in the core-collapse case may have smallerMb,iand Ωicompared to those produced in the merger case.Therefore,in the former case,the initial baryonic mass and angular velocity are taken to be as low asMb,i=1.4M⊙and Ωi=0.2ΩK,respectively.To see how their values can affect the results,a largerMb,i=2.1M⊙or Ωi=ΩKis also taken while other quantities are kept unchanged.In the latter case,Mb,i≥2.7M⊙and Ωi≥0.5ΩKare adopted.We note that some remnant NSs left in BNS mergers may actually haveMb,i>2.7M⊙,however,to grasp the whole evolution process of a newborn magnetar and thus avoid collapsing to a BH,the minimum initial baryonic mass is set asMb,i=2.7M⊙.For comparison,a largerMb,iis also adopted to show how its value can affect the GW radiation.For both the core-collapse and the merger cases,the radii of newborn magnetars are taken to beR=12 km.We first show the results for the core-collapse case. The evolution of ν,Mg,ζ andBdof newborn magnetars with various values ofMb,iand Ωi(as shown in the legends) are presented in Figure 1.Hereinafter we refer to the case in which FADD is involved as the decay case.First we use Model II witha2=−3 to describe the decay ofBddue to accretion.Evolution of the physical quantities of magnetars in this case are shown by the solid lines in Figure 1.For comparison the dashed lines represent the results calculated by assuming a constantBd(hereinafter referred to as the non-decay case).Since for the set of fall-back parametersMfb=0.8M⊙andtfb=1000 s,and the set of magnetar parametersBd,i=1015G and Ωi=ΩK,the magnetar spins so fast that it enters into the propeller phase immediately when fall-back accretion occurs and subsequently approaches the so-called spin equilibrium(Rm=Rc)with its spin frequency evolving as ν ∝t−5/7(Dai&Liu 2012).No fall-back matter can be accreted onto the magnetar during its whole evolution,hence bothMgandBdremain unchanged even if FADD is involved.The evolution of the magnetar is totally the same as that in the non-decay case.Therefore,the emitted GW signals in the two cases have no difference,as presented by the red solid and black dashed lines in Figure 3,which show the evolution of characteristic amplitudehcversus emitted frequency νeof the GW signals.For brevity,in Figure 1 we only show the results of the decay case(red solid lines).For the magnetars with lower initial spin Ωi=0.2ΩK,no matter whether FADD is considered,their ν andMgall increase at first since matter can be accreted onto them.However,the increases are much more obvious in the decay case because more matter can be accreted for magnetars with decayingBd.After accreting enough matter,in the decay case,the dipole fields of these magnetars would quickly reach the minimum strengthBd=1011G,thus the GW radiation spin-down becomes dominant (ν ∝t−1/4).Moreover,in this case,the magnetar would collapse to a BH at ∼2×105s if it has a large initial massMb,i=2.1M⊙,whereas in the non-decay case,such a magnetar would be eternally stable.The results in Figure 1 therefore suggest that the spin and gravitational mass evolutions and further the lifetime of newborn magnetars would be dramatically altered if fall-back accretion can indeed lead to field decay.From Figure 1 we also find that the dynamical bar-mode and secular instabilities are not activated as ζ<0.1 is kept during the whole evolution process of the magnetars. We also compare the results obtained by using Model II witha2=−3 (red lines) to those derived by using Model II,however,witha2=−0.5(green lines)and Model I(blue lines),as shown in Figure 2.By changinga2=−3 toa2=−0.5,the evolutions of the magnetar remain basically unchanged except thatBdis finally slightly larger fora2=−0.5.Nevertheless,GW radiation spin-down is still dominant.Consequently,in the following calculations when using Model II,we will only takea2=−3.In contrast,if Model I is used to describe FADD,Bdwould not decay sincealways holds for the set ofBd,i,Mfbandtfbadopted. Figure 1.Evolution of the spin frequency ν,gravitational mass Mg,ratio of rotational energy to the absolute value of gravitational energy ζ,and dipole magnetic field Bd of newborn accreting magnetars formed in the core-collapse case.Different values for the initial angular velocity Ωi and initial baryonic mass Mb,i of the magnetars are adopted,as shown in the legends.The solid lines represent the results of the decay case,in which Model II with a2=−3 is used to describe FADD.The dashed lines show the results of the non-decay case. In Figure 3,we present the evolution of characteristic amplitudehcversus emitted frequency νeof GW signals emitted by newborn magnetars formed in the core-collapse case.The solid lines represent the results of the decay case(Model II),while the dashed lines show the results of the nondecay case.Here,ΩiandMb,iare taken to be the same as in Figure 1 (see the legends).For magnetars with lower initial spin Ωi=0.2ΩK,the differences in the emitted GWs between the decay and non-decay cases are quite remarkable.If fallback accretion could indeed lead to dipole field decay,the emitted GW signals would be much stronger and extend to much higher frequencies because the magnetars can be considerably spun up due to their weakBd.These signals may even be detectable by aLIGO at its design sensitivity,while in the non-decay case,the signals may only be detected by ET.Therefore,for newborn magnetars born in the corecollapse case,if they have lower initial spin Ωi=0.2ΩK,through observations of the GWs from these magnetars we may distinguish whether fall-back accretion could lead to dipole field decay or not.On the other hand,as found in Figure 1,in both cases,since magnetars with Ωi=0.2ΩKcan be spun up first due to fall-back accretion and then spun down mainly due to GW radiation(the decay case)or torques exerted by the disks (the non-decay case),hence there are transition points between the spin-up and spin-down processes,at whichare rather small.The smallewould give rise to spikes in the evolution curves ofhcversus νein Figure 3.The frequencies at which the spikes appear are much higher in the decay case in comparison with the non-decay case because the magnetars in the former case can be spun up to much higher frequencies.Consequently,the spike in thehc−νecurve can be regarded as the evidence of fall-back matter being accreted onto the newborn magnetar.Finally,in the decay case the collapse of the magnetar with Ωi=0.2ΩKandMb,i=2.1M⊙could manifest as a catastrophic cutoff in the GW signal at νe≃500 Hz,which may be observable by aLIGO at design sensitivity for the large amplitude ofhc≃3×10−22at this point. Figure 2.Evolution of ν,Mg,ζ,and Bd of newborn accreting magnetars formed in the core-collapse case when FADD is considered.Different field decay models are adopted to describe FADD,as shown in the legends.Here we take Mb,i=1.4M⊙and Ωi=0.2ΩK. We now focus on the evolution of magnetars produced in the merger case and the emitted GW signals.In Figures 4–7,we fixMb,i=2.7M⊙andMfb=0.1M⊙.A comparison of the evolution of magnetar’s physical quantities between the decay (Model II witha2=−3) and non-decay cases is shown in Figure 4 (see the legends),while a comparison of the corresponding GW signals is presented in Figure 6.For the set of fall-back parametersMfb=0.1M⊙andtfb=0.1 s considered here,the initial accretion rate is so high that matter can be accreted onto the magnetar even if it has a very fast initial spin of Ωi=ΩK.Consequently,in the decay case,for the magnetar with Ωi=ΩK,itsBdwould rapidly decline to 1011G,whereas itsMgwould rapidly increase and then become saturated.Varying Ωifrom ΩKto 0.5ΩK,the evolution ofBdandMgremain unchanged,however,the spin-up feature gradually becomes remarkable.After the spin-up,the magnetar spins down dominantly through GW radiation because of its lowBdin the decay case.In contrast,in the non-decay case,the magnetar with the same Ωiwould finally have a lowerMgand spin down mainly due to propeller effect after the early spin-up stage.Furthermore,with the decrease of Ωi,Mgwould finally saturate at a larger value.Again,for all cases and initial conditions considered here,during the evolution of newborn magnetars we always have ζ<0.1,hence GW radiation from bar-mode and secular instabilities can be neglected. The remarkable differences in the emitted GW signals between the decay and non-decay cases are presented in Figure 6.The results show that if fall-back accretion could indeed lead to dipole field decay of newborn magnetars,the emitted GWs would be dramatically enhanced,especially at νe≾860 Hz,making them even be detectable by aLIGO at design sensitivity.The reason is that in the decay case afterBdis reduced due to accretion,GW rather than propeller spindown becomes the dominant channel of losing rotational energy of the magnetars.The diverse evolution behaviors ofhcversus νeof the GWs in the two cases may be distinguishable by using ET provided that the magnetars can sustain for a relatively long time,namely,the merger remnants are eternally stable or temporarily stable magnetars.Therefore by virtue of ET,observations of the GWs from BNS merger remnants may not merely help to identify the existence of eternally stable or temporarily stable magnetars but also figure out whether fallback accretion could result in dipole field decay.On the other hand,for both the decay and non-decay cases,spikes appear at νe>1670 Hz in thehc−νecurves (see Figure 6),which are also a sign of matter being accreted onto the newborn magnetars.Note that the complex structures in thehc−νecurves of the non-decay case are a result of complicated spin evolution of the magnetars. Figure 3.Evolution of the characteristic amplitude hc with emitted frequency νe of GWs from newborn accreting magnetars produced in the core-collapse case.We take different values for Ωi and Mb,i,and make a comparison of the results obtained with and without FADD involved,as shown in the legends.The rms strain noises for LIGO(light-gray solid line),Virgo(light-gray dashed line),aLIGO at design sensitivity(light-gray dotted line),and future ET(lightgray dashed–dotted line) are also shown for contrast (Sathyaprakash &Schutz 2009). In the decay case,we also explore whether different field decay models (Model I versus Model II witha2=−3) could lead to different evolution behaviors of the magnetar and GW signals.The results are respectively shown in Figures 5 and 7.In the merger case,initially the accretion rate is so high that the conditionsandRc>Rmare satisfied,hence if Model I is considered,Bdwould decrease to 1011G at the onset of the evolution.By involving Model II witha2=−3,it is shown in Figure 5 thatBddecays to 1011G only ∼0.1 s after the onset of the evolution.Therefore in the merger case,for the two field decay models considered,the rather tiny difference in the evolution ofBdcannot give rise to obvious differences in the magnetar’s evolution and the emitted GW (see Figure 7). In Figure 8,we show the effects ofMb,iandMfbon the emitted GW signals in the merger case.Here we adopt Model II witha2=−3 for the field decay model and Ωi=ΩK.For a fixed fall-back massMfb=0.1M⊙,an initially heavier magnetar withMb,i=2.8M⊙will collapse at a higher frequency and result in a catastrophic cutoff in the GW signal at νe∼1000 Hz for EOS GM1 considered.On the other hand,if the magnetar with the same initial massMb,i=2.8M⊙is surrounded by a smaller fall-back disk (Mfb=0.01M⊙),its emitted GW could extend to much lower frequencies,possibly be detectable by aLIGO at design sensitivity.Therefore,the relatively lowfrequency GW(νe≾1000 Hz)from the newborn magnetar that has a large initial mass and is surrounded by a large fall-back disk may be undetectable. Figure 4.Evolution of ν,Mg,ζ,and Bd of newborn accreting magnetars produced in the merger case with(colored lines)and without(black lines)considering FADD.Here we take Mfb=0.1M⊙and the magnetars are assumed to have the same initial baryonic mass Mb,i=2.7M⊙,however,different Ωi.See the legends for details. Figure 5.Evolution of ν, Mg,ζ,and Bd of newborn accreting magnetars produced in the merger case with FADD involved.We make a comparison of the results derived with Model I and Model II (a2=−3).The same as in Figure 4,different values for Ωi are taken.See the legends for details. Figure 6.The characteristic amplitude hc vs.emitted frequency νe of GWs from newborn accreting magnetars with different Ωi produced in the merger case with and without FADD involved,as shown in the legends.Here we take Mb,i=2.7M⊙and Mfb=0.1M⊙.The same as in Figure 3,the rms strain noises for LIGO,Virgo,aLIGO at design sensitivity,and future ET are also shown. Figure 7.hc vs.νe of GWs from newborn accreting magnetars with different Ωi produced in the merger case with FADD involved.We make a comparison of the results derived with Model I and Model II (a2=−3).We take Mb,i=2.7M⊙and Mfb=0.1M⊙.The same as in Figure 3,the rms strain noises for LIGO,Virgo,aLIGO at design sensitivity,and future ET are also shown.See the legends for details. Figure 8.hc vs.νe of GWs from newborn accreting magnetars produced in the merger case with FADD involved.Here we take Ωi=ΩK and Model II(a2=−3)is used.As shown in the legends different values for Mb,i and Mfb are adopted in order to see how these can affect the final results.Also shown are the rms strain noises for LIGO,Virgo,aLIGO at design sensitivity,and future ET. Figure 9.hc vs.νe of GWs from the putative NS remnant of GW170817.Here we take Mb,i=2.855M⊙and Ωi=ΩK for the NS,and Mfb=0.1M⊙for the disk.We make a comparison of the results obtained with and without FADD involved,and by assuming different NS EOSs,as shown in the legends.The stars represent the upper limits set by post-merger GW searching results of GW170817 obtained by aLIGO and aVirgo (see the text for details).Also shown are the rms strain noises for LIGO,Virgo,aLIGO at design sensitivity,and future ET. The nature of the merger remnant of GW170817 is still under debate and has attracted great research interests since this issue is tightly related to the highly unknown NS EOS(e.g.,Margalit&Metzger 2017;Ai et al.2018,2020;Rezzolla et al.2018;Ruiz et al.2018;Shibata et al.2019).Plenty of observations of the EM counterparts of GW170817 have been used to pose constraints on the properties of the merger remnant(e.g.,Margalit&Metzger 2017;Ai et al.2018,2020;Geng et al.2018;Pooley et al.2018;Rezzolla et al.2018;Ruiz et al.2018;Yu et al.2018;Li et al.2018;Gill et al.2019;Lü et al.2019b;Piro et al.2019;Shibata et al.2019).The blue kilonova signature observed in GW170817 and the upper limits on the energy of the GRB jet and kilonova ejecta indicate that the remnant could be a hypermassive NS or very short-lived supermassive NS (Margalit &Metzger 2017;Gill et al.2019).This scenario for the merger product is also supported by the suggestion that a BH central engine is needed to produce GRB 170817A,which could simply result from the collapse of such an NS remnant (Rezzolla et al.2018;Ruiz et al.2018;Gill et al.2019).However,a stable massive or at least a long-lived supermassive NS remnant was also proposed to be consistent with observations.7Hereinafter,when discussing the merger product in GW170817,for brevity,we refer to both the stable massive and the long-lived supermassive NS remnants as the long-lived NS remnant,unless otherwise noted.Ai et al.(2020)performed a comprehensive study on the allowed parameter space of the putative long-lived NS produced in GW170817 and found that a long-lived NS remnant cannot be excluded based on the GW and EM observations of this event.The brightening in the multiband emissions up to 100 days after GW170817 may be caused by the interaction between the wind from a long-lived NS remnant and the jet (Geng et al.2018),though the X-ray emission observed by Chandra at 107 days seems to favor a BH remnant (Pooley et al.2018).Moreover,the X-ray flare discovered at 155 days after the merger,despite a low significance,may be just the result of the sudden reactivation(Piro et al.2019) or even the collapse of the long-lived NS remnant(Lü et al.2019b).Finally,the long-lived NS remnant scenario is also favored by observations of the kilonova AT2017gfo of the GW170817 event (Li et al.2018;Yu et al.2018). The best and direct way to determine the properties of the remnant of a BNS merger is searching for post-merger GW signals.For GW170817,if the remnant is a long-lived NS,as indicated by some observational evidences mentioned above,may produce long-lasting GW radiation.However,direct searches for post-merger GWs by aLIGO and aVirgo have shown null results and only GW strain upper limits were given(Abbott et al.2017c).Nevertheless,detection of the postmerger GWs from an event similar to GW170817 using aLIGO at design sensitivity and ET is still promising (Abbott et al.2017c),and constraints on the nature of the merger remnant may then be set.The most intriguing issue is that if the remnant of GW170817 is a long-lived NS,it should have a relatively low surface dipole fieldBd∼1011−1014G,however,a much higher internal toroidal field~ 1015-1016G,so as to be consistent with some EM observations(Ai et al.2018;Li et al.2018;Yu et al.2018;Geng et al.2018;Piro et al.2019;Lü et al.2019b).It has been proposed that such a special NS may originate from a newborn magnetar whose dipole field was buried and reduced due to fall-back accretion of the disk matter surrounding the magnetar (Yu et al.2018). In this section,we apply our model to the discussions of formation of a long-lived NS remnant with weak dipole but strong toroidal fields in GW170817 and the magnetically induced GW radiation during its evolution.We aim to investigate whether future detection of the post-merger GWs from an event similar to GW170817 using aLIGO at the design sensitivity and ET could support or disfavor the dipole field burial scenario.In other words,we would like to know whether GW detection could help to answer if such a special NS could be formed due to fall-back accretion or not. Following Dai (2019),the total baryonic mass of the BNS system of GW170817 is assumed to beMb,tot≃3.02M⊙.After subtracting the ejecta (Mej≃0.065M⊙,Villar et al.2017) and disk masses (Mfb=0.1M⊙or 0.01M⊙as discussed in Section 2),the putative long-lived NS remnant should have an initial baryonic massMb,i=2.855M⊙or 2.945M⊙.Initially,the NS is assumed to rotate at the Keplerian limit with itsBd,iandbeing taken the same as in Section 4.We use Model II witha2=−3 to describe the decay ofBddue to fall-back accretion.In case of complete burial the minimum strength is also taken to beBd,min≈ 10-4Bd,i=1011G,which is basically consistent with the required value forBdin Yu et al.(2018).Since the values forBdandof the NS remnant of GW170817 inferred from the EM observations are distributed in wide ranges and no value can be found to satisfy all the observations,we are not required to choose values forBd,i,andBd,minin order to make the resultantBdandbe entirely consistent with all the observations.In fact,the initial values and the minimum strength we adopted are mainly based on theory(see Sections 3 and 4). In Figure 9,we show a comparison of the GW signals emitted by the putative NS remnant left in GW170817 with and without the FADD involved (see the legends).Here we takeMfb=0.1M⊙and thusMb,i=2.855M⊙.We considered two typical NS EOSs:GM1 versus DDME2(see Ai et al.2020 and references therein).Using a series of bar-mode waveforms and assuming a 50% detection efficiency,the aLIGO and aVirgo collaboration searched the post-merger GWs from the remnant of GW170817 in the frequency ranges fromf0=449 toff=139 Hz and fromf0=356 toff=111 Hz,and obtained the best upper limits on the root-sum-squared strain amplitudes of GWs emitted in the two ranges asand 5.9×10−22Hz−1/2,respectively (see Table 2 in Abbott et al.2017c).These upper limits on the GW strain amplitudes can be further converted into upper limits on the characteristic amplitudes of GWs emitted at frequenciesfc=(f0+ff)/2 aswhich are represented by the solid stars in Figure 9.Althoughhcuppare derived in a very rough way here,this does not hinder us from making an order-ofmagnitude comparison betweenhcuppandhcfrom our theoretical calculations.Following the same method,we can also convertobtained by using a series of magnetar waveforms in post-merger searches intohcupp(Abbott et al.2017c),as shown by the hollow stars.Note that for the searches using magnetar waveforms,we have only adopted (the best)derived by assuming a more reasonable ellipticity of 10−3(see Table 3 in Abbott et al.2017c for details). Obviously,hcuppderived from post-merger GW searching results of GW170817 are several tens to about 100 times larger than our theoretically calculatedhcof GWs emitted by the putative NS remnant.Therefore from the upper limits given by aLIGO and aVirgo,we cannot deduce whether the merger product is a long-lived NS,much less to determine whether itsBdhas decayed due to fall-back accretion.In fact,when EOS GM1 is adopted,the merger remnant should be a supermassive NS whose GW radiation is terminated at ∼1500 Hz ifBddecayed because of accretion,while at ∼1380 Hz ifBdwas not affected by accretion.The differences in thehc−νecurves between the decay and non-decay cases are marginal except the very high frequency (νe≿2390 Hz) part.It may thus be difficult to find out the evidence of FADD using aLIGO at design sensitivity and even ET provided that the dense matter EOS is described by GM1.However,for the EOS DDME2 with largerMTOV,the merger remnant could exist as a stable massive NS for a long time in both the decay and the nondecay cases.As shown in Figure 9,the GW radiation in the two cases differ remarkably withhcbeing enhanced by a factor∼2–100 at νe≾1000 Hz in the decay case.We note that this difference may be distinguishable for aLIGO at design sensitivity and ET.Similar results are also shown in Figure 10,in which the disk mass is set asMfb=0.01M⊙(thusMb,i=2.945M⊙).We thus suggest that if the post-merger GWs from GW170817-like events could be detected using these more sensitive GW detectors in the future,we may not only exclude the dense matter EOSs with smallMTOVbut also figure out whether fall-back accretion could lead to dipole field decay of the long-lived NS remnants. Figure 10.The same as in Figure 9, hc vs.νe of GWs from the putative NS remnant of GW170817 are shown.However,we take Mb,i=2.945M⊙for the NS and Mfb=0.01M⊙for the disk here. In view of the observed EM radiation from some LGRBs,SGRBs and NSs,and the theoretical models raised to explain these observations,whether fall-back accretion could lead to dipole field decay of newborn NSs is still an open issue.In this paper,we investigate the evolution and GW radiation of newborn magnetars with a fall-back disk in both the corecollapse and the merger cases and intend to figure out whether FADD is relevant for newborn accreting magnetars through detection of GW radiation from these magnetars.We make a comparison of the results obtained with and without FADD involved.Two phenomenological models,namely,the accretion-rate-dominated (Model I) and accreted-mass-dominated (Model II) models are adopted to describe FADD.We find that in the core-collapse case when Model II is adopted,the dipole fields of newborn accreting magnetars would show a remarkable decay if their initial spins are less than the Keplerian limits.However,when Model I is used,their dipole fields would not decay.As a comparison,in the merger case,no matter Model I or Model II is adopted,the dipole fields of newborn accreting magnetars would obviously decay after their birth even if they spin at the Keplerian limits initially.Our results show that in both the core-collapse and the merger cases,the evolution of newborn accreting magnetars and the GW radiation from these magnetars could be dramatically altered if FADD indeed plays a role.Specifically,for the fallback parameters and initial parameters of magnetars used,in most cases when FADD is taken into account,the dipole fields could be reduced toBd=1011G.As a result,the newborn accreting magnetars would be spun up to higher frequencies and have larger masses as compared to the non-decay cases.Therefore,with the presence of FADD,the GW radiation of newborn magnetars would probably be prominently enhanced and extend to higher frequencies.We suggest that detection of GW signals from newborn magnetars by future detectors such as the aLIGO at design sensitivity and ET may help to diagnose whether FADD could occur during the early evolution of these magnetars.Moreover,when FADD is considered,the magnetars would be more liable to collapse to a BH and result in a catastrophic cutoff in the emitted GW signals.Observation of the cutoff frequencies of the GW signals may give some constraints on the NS EOSs. The remnant of GW170817 has been suggested to be a special long-lived NS whose dipole field has decayed due to fall-back accretion (Yu et al.2018).We also apply our model to the discussion of the nature of GW170817 remnant.We propose that from the post-merger GW searching results given by aLIGO and aVirgo we cannot confirm whether the remnant of GW170817 is a low-dipole-field long-lived NS.However,if the merger remnants of GW170817-like events are indeed long-lived NSs,that is,EOSs with largeMTOV(e.g.,EOS DDME2) are favored,future observations of GWs from such events by the aLIGO at design sensitivity and ET may provide us a definite conclusion about whether FADD is valid in newborn NSs produced by BNS mergers.Meanwhile,detection of GWs from GW170817-like events will undoubtedly set constraints on the dense matter EOSs. Although we have made a detailed investigation about the evolution and associated GW radiation of newborn accreting magnetars born in the core-collapse and merger cases,and made a comparison of the results obtained with and without FADD involved,some further improvements are still in need.First,in this paper we adopt two phenomenological models to describe FADD of newborn accreting magnetars for simplicity.Detailed MHD simulation of the field burial process of newborn accreting magnetars is still necessary since this will tell us how the dipole fields evolve with time during the accretion process.The reason is that different evolution behaviors of dipole fields of magnetars may lead to distinct GW radiation.Second,the evolution ofRof newborn accreting magnetars is neglected here,thus the evolution ofIis calculated in a rough way.Sophisticated calculation of the evolutions of magnetar parametersMg,RandIusing the RNS code (Stergioulas &Friedman 1995) as that done in Sur &Haskell (2021) is also indispensable in order to obtain more realistic GW signals from newborn accreting magnetars.Finally,the accretion mountains on the magnetic poles of newborn accreting magnetars may also produce significant GW radiation (Melatos &Priymak 2014;Sur &Haskell 2021) and how this can affect the magnetically induced GWs is worthy of further investigation.We will make further investigation on some aspects of the issues mentioned above in a subsequent paper. Acknowledgments We thank the anonymous referee,S.N.Zhang,and Y.W.Yu for their helpful comments.This work is supported by the National Natural Science Foundation of China (Grant Nos.12 003 009,12 033 001,and 11 922 303),CAS “Light of West China” Program (Grant No.2019-XBQNXZ-B-016),the National SKA program of China (Grant No.2020SKA0120300),and Scientific Research Project Fund of Hubei Provincial Department of Education (Grant No.Q20161604).2.Evolution of Newborn Accreting Magnetars
3.Fall-back Accretion-induced Dipole-field Decay
4.Results
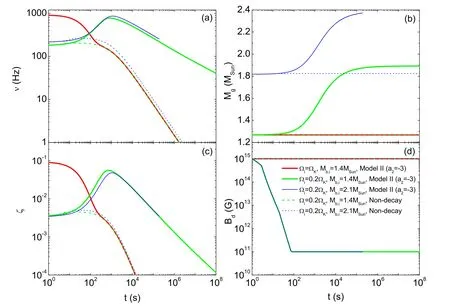
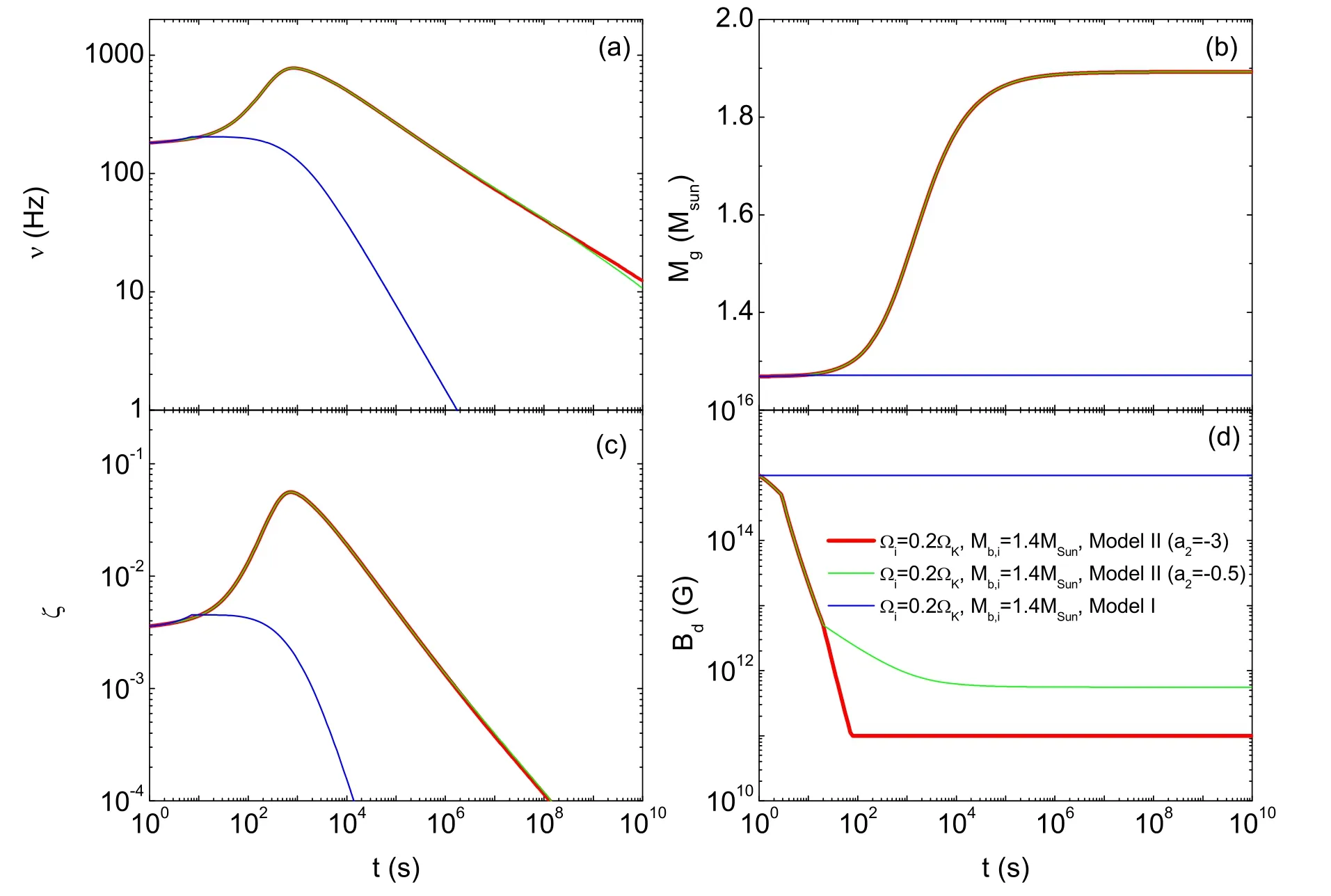
4.1.The Core-collapse Case
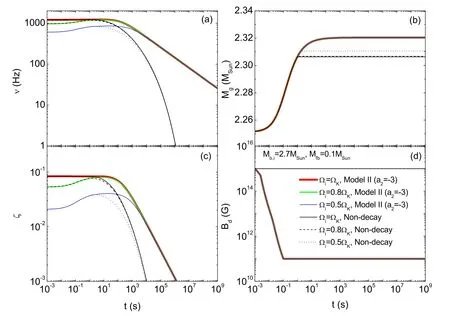
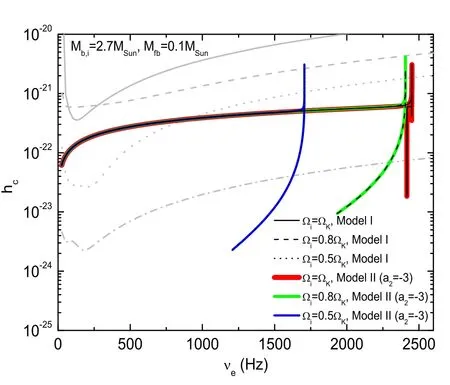
4.2.The Merger Case





5.Application to GW170817

6.Conclusion and Discussions
杂志排行
Research in Astronomy and Astrophysics的其它文章
- Application of a Magnetic-field-induced Transition in Fe X to Solar and Stellar Coronal Magnetic Field Measurements
- Simulation-driven Wind Load Analysis and Prediction for Large Steerable Radio Telescopes
- Power-law Distribution and Scale-invariant Structure from the First CHIME/FRB Fast Radio Burst Catalog
- Solar Active Region Magnetogram Generation by Attention Generative Adversarial Networks
- Construction and Validation of a Geometry-based Mathematical Model for the Hard X-Ray Imager
- The Decay Process of an α-configuration Sunspot
