关于2022年一道高考物理题的分析与拓展

侯奕龙 曾启轩 王梓宁 李 惠

(湖南省株洲市第二中学，湖南 株洲 412000)

真题(2022年湖南卷第5题).2022年北京冬奥会跳台滑雪空中技巧比赛场地边有一根系有飘带的风力指示杆，教练员根据飘带的形态提示运动员现场风力的情况.若飘带可视为粗细一致的匀质长绳，其所处范围内风速水平向右，大小恒定且不随高度改变.当飘带稳定时，飘带的实际情况最接近的是(如图1所示)

图1

这是2022年高考物理湖南卷第5题，正确答案是(A).最常见的错误思路如下：稳定后飘带所受的空气阻力(后面简称为风力)一定，取包括自由端在内的一段飘带分析，其上端点越靠近固定端，该段重力越大，重力、风力的合力方向越靠近竖直轴.而上端所受拉力沿切线方向且与其他两力合力平衡，越靠近固定端处的切线越陡，所以错选(B).

但事实真是如此吗？下面做一个小实验来验证.

1 实验验证与理论分析

准备一台风扇(风速在出风口一定范围内较为均匀,符合题设情境)和一根粗细均匀的柔软细绳.固定细绳一端，让其余部分全部位于出风口处，结果如图2所示.从中可以看出细绳几乎是一条直线，这是为什么呢？

图2 匀质绳子在均匀空气阻力下的形状

均质长绳中任取一绳段，其重力、均匀风力对于每一段均质绳段来说，都是相同的，我们不妨把这两个恒力作为等效重力，即每一段绳段都处于恒定的等效重力场中，这条均质绳自然只能在等效重力场中沿等效重力方向悬挂成一条直线.

大量考生选错的另一个原因是生活中有些带状物随风舞动时为图1中选项(B)或者(C)的形状，这又是为什么呢？我们进一步做实验来模拟.

2 实验拓展与进一步理论分析

2.1 拓展实验现象

如图3所示，若在均质绳末端挂一小重物(可视为质点)，则绳的形状不再是直线，此时绳子的形状最接近选项(C).若在绳子末端系一个重力几乎为零，风力受力面积更大的物体(称为阻力物)，待其稳定后绳子最接近于选项(B)(如图4所示).

图3 绳子末端夹磁铁的形状

图4 绳子末端加高阻力物的形状

风扇的风速受距离影响，并不均匀,为得到均匀风速，可在封闭环境用无人机吊着绳子匀速飞行.图5、图6为无人机下用均质缆绳悬吊重物的情况，重物如图7所示的小铁球.

图5

图6

图7

2.2 拓展实验的半定量理论分析

把均质绳粗略地分成质量相等的3段，每段质量记为m，重物质量记为M，则对第1段均质绳，重物，受力分析如图8所示，从图中可以看出，第2段绳对第1段的拉力方向更贴近竖直方向.

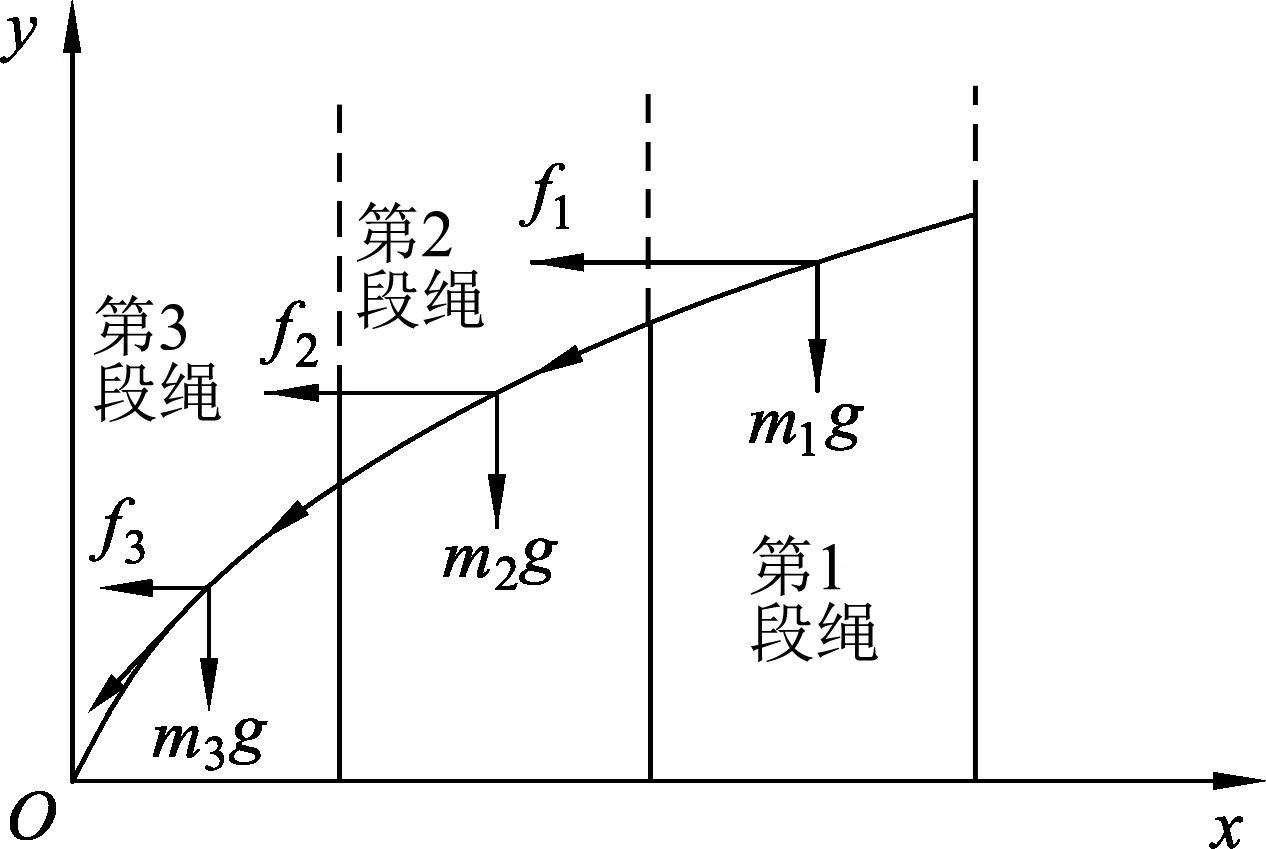
图8 半定量分析

2.3 拓展实验的定量理论分析

现在用微分方程分析3种情况下绳子的形状.

绳子末端挂有一物体，该物体受到的空气阻力为F，其质量为M，设空气流速为v=1 m/s，空气密度ρ=1.29 kg/m3，重力加速度g=9.80665 m/s2，该绳子的空气阻力系数为C=0.5，绳子的宽度为d=0.001 m，质量线密度为λ=0.001 kg/m.

图9

(1)

其重力为

(2)

在x处绳子的张力为T(x)，则x方向上

Tx(x+dx)=Tx(x)+df,dTx=df.

(3)

当x=0时，Tx=F.

在y方向上

Ty(x+dx)=Ty(x)+dG，dTy=dG.

(4)

又有

Ty=y′·Tx，dTy=y″·Tx·dx+y′·dTx.

(5)

联立(1)～(5)式，解得

(6)

初值条件为

(7)

由于该微分方程十分复杂，无法解出严格解，以下为通过数值描点用Mathematica作出来的图像.

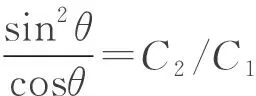
图10 Mathematica描点作图

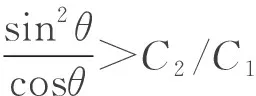
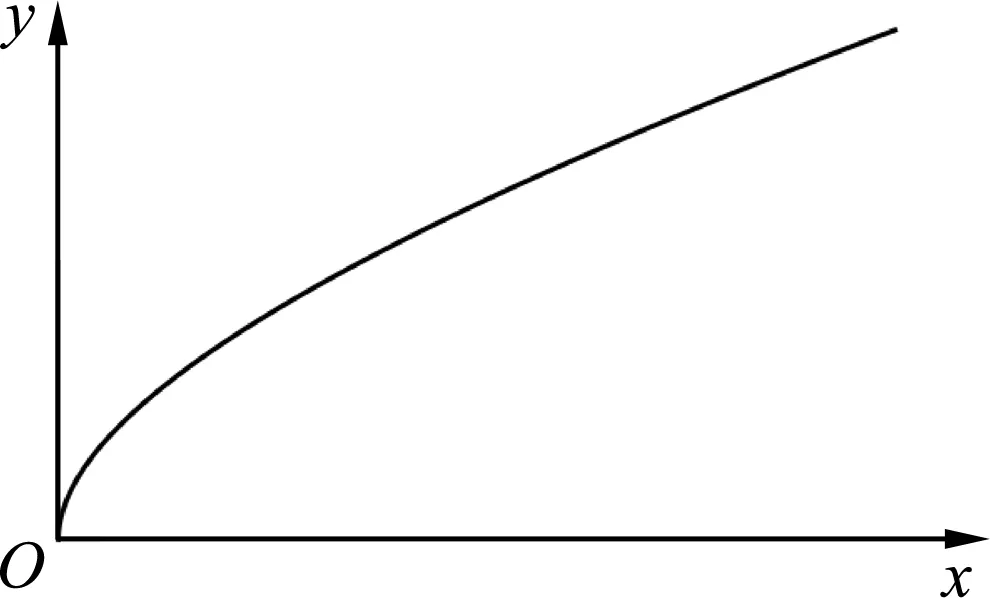
图11 Mathematica描点作图

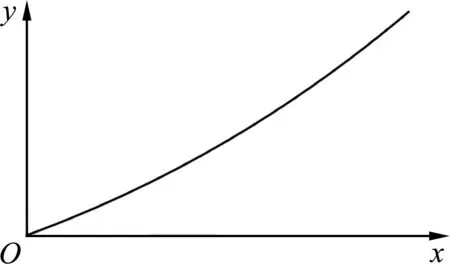
图12 Mathematica描点作图

综上所述，图1中选项(A)是均质绳在均匀水平风力中的形状；选项(B)和(C)是非均质绳在均匀水平风力中的形状，或者说是均质绳在非均匀水平风力中的形状.