基于RSM和NSGA-Ⅱ法的重载机械臂结构优化设计
2023-03-23魏文清郑雪楷
魏文清 刘 放 郑雪楷 杨 言
西南交通大学机械工程学院 成都 610031
0 引言
隧道施工环境复杂多样,在险峻地形下作业难免会遇到极大安全风险[1]。为应对隧道的复杂工况,施工作业机械臂被广泛引入到施工一线[2]。当前,高负载下的工程作业机械臂存在控制精度不足、冗余质量过高等问题,为了实现机械臂更高的控制精度,首先要实现更可靠的机械臂结构,需要在静刚度、强度满足许用要求的情况下拥有更好的截面参数,以实现更精确的控制[3]。
在目前的结构件设计中,以经验或半经验导向的结构设计依然处于设计方法的主要地位[4]。为此,对于复杂结构难以得出结构截面参数与实际所需优化目标的显式表达式问题,由Box GEP等[5]提出的响应面方法(RSM)逐步成为一种行之有效的设计思路;孙喜龙等[6]利用响应面方法优化了轿车车身防撞性能;刘德仿等[7]利用响应面方法对喷印机结构进行了结构参数优化。
目前,运用响应面分析模型优化机械结构参数的方法被越来越多地运用于工程实际问题中,对响应面模型求解在结构优化设计中成为不可或缺的一环。随着各类智能算法的发展,利用智能优化算法求解多变量非线性优化问题亦成为趋势。包世刚等[8]利用多目标遗传算法求解动车组水箱的响应面模型提出了复杂模型的结构优化设计。
在目前的机械臂设计中,利用经验公式与仿真试验结合的方法已无法满足实际需要,故而利用响应面方法建立数学模型并结合智能算法的求解是大势所趋。
1 液压重载机械臂优化方法
1.1 传统响应面优化方法
传统响应面方法一般用于优化设计中,即通过合理的实验设计方法解决目标的建立、约束与设计变量之间的近似函数等问题。其实验设计概括如下:
1)在某个样本点(高维空间的点)做实验,其中1组设计变量x=(x1,x2,…,xn)T为一个样本点,得到1个未知性能的结果(即样本值)。
2)为了得到未知性能相应的函数,1个样本值远远不够,欲取多个样本点就要涉及1组样本点在高维空间中的排放问题,即实验设计方法。其基本理论为:对于未知的待求性能函数y=y(x)难以找出准确表达式,但对于给定的参数点或设计点则可通过实体或数值实验得到相应性能值y j=y(x(j)),这是对应相应参数点或设计值的一个响应值。
因此,对于足够多的实验(如m个实验),即可利用m个样本点及其所产生的m个响应(即性能的样本值),利用待定系数的方法求出函数y=y(x)的近似函数,即
式中:为待构造的响应面函数,f(x)为性能函数,ε为误差项。
一般地,采用含交叉项的二次型函数可表示为
式中:α0为常数项待定系数αj为一次项待定系数,αij为二次项待定系数,βi为待定系数。
1.2 通过中心展开点的改进响应面优化方法
当迭代收敛时,传统响应面优化方法存在约束在当前设计点(中心点)不能严格满足约束条件的问题。因此,传统响应面方法在中心设计点拟合值不精确,现采用通过中心展开点的改进响应面模型[9]。对机械臂优化问题建立通过中心展开点的改进响应面模型,其基本思想有2点:
1)在实验点中选取一点x(0),响应面函数在该点取值等于实验值y(0),即[x(0)]=y(0),称该点为中心展开点;
2)响应面函数在其余m-1个实验点的取值与实验值的误差满足最小二乘法的原则。将中心展开点代入式(2)可得
将式(3)代入式(2)可得
定义响应面函数值与真实值之间的误差ε=(ε1,ε1,…,εm-1)T表示为
对其他实验点做最小二乘拟合,可得
由驻值条件得到
将其以矩阵形式表示为
得到解为
将其代入式(3)求得β0,将β0代入响应面函数可得通过中心展开点的响应面模型为
1.3 多目标非支配排序遗传算法(NSGA-Ⅱ)
采用多目标非支配排序遗传算法(NSGA-Ⅱ)求解响应面模型,其优势在于将非支配分类程序引入,通过将多个目标简化为单个适应度函数的评价方式[10]。与传统的遗传算法相比,该算法的优势是在选择算子执行前依据个体间的支配关系对种群进行分层排序。在进行支配关系排序后,将非支配个体作为一类处理来共享虚拟适应度值,进而对种群剩余个体分级并赋予相应虚拟适应度函数值。其优化流程如图1所示。
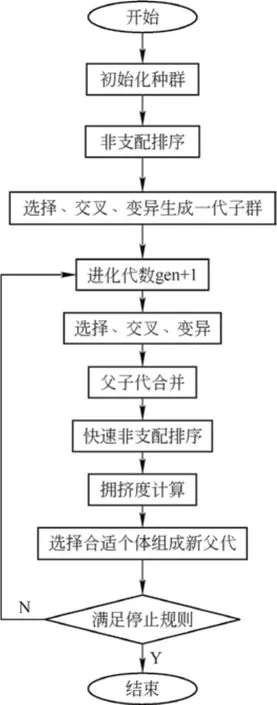
图1 多目标非支配排序遗传算法(NSGA-Ⅱ)优化流程
2 液压重载机械臂优化模型构造
2.1 液压重载机械臂构组成
液压重载机械臂为六自由度多关节机器人,其结构如图2所示。液压重载机械臂主要由转台、二级伸缩臂、折臂回转机构、折臂、飞臂及末端执行器等组成,由液压驱动,含有2个液压马达、变幅液压缸、伸缩液压缸、折臂液压缸、飞臂液压缸。其中,初级回转支承、折臂回转机构均为内外圈结构的回转减速器的结构形式,采用液压马达和蜗杆蜗轮驱动,具有自锁功能。回转支承外圈固定安装于车架顶面。
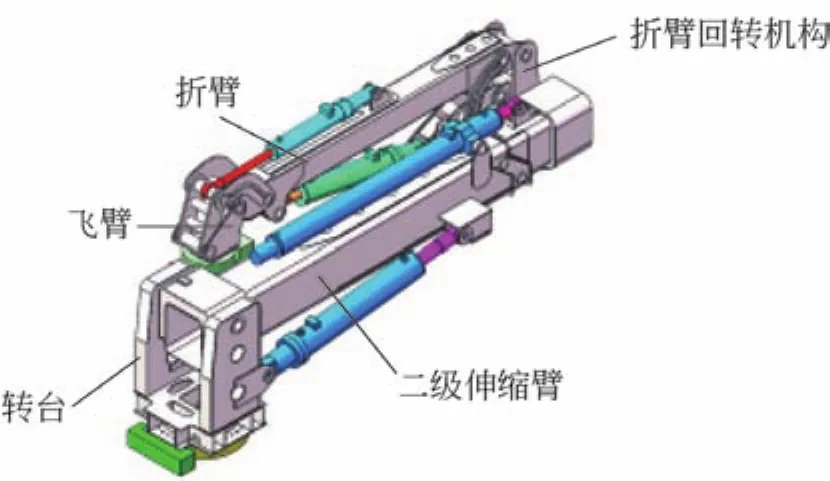
图2 液压重载机械臂结构
在液压重载机械臂运动过程中,主要承力的部件为二级伸缩臂部分,为此本次着重构建重载机械臂二级伸缩臂的参数模型,基于此模型建立响应面模型并最终完成优化。
2.2 液压重载机械臂力学模型分析
二级伸缩臂在变幅平面内进行受力分析时,不仅需要考虑伸缩臂及其后端负载对二级伸缩臂臂架结构的弯矩载荷,也应考虑回转平面内折臂、飞臂和抓取重物对二级伸缩臂的扭矩载荷。在二级伸缩臂外伸展开过程中,一节臂与二节臂之间的重叠部分逐渐减少,二节臂外伸至最远端时的重叠面积最小,存在相互脱离趋势,会产生危险截面。
为了保证整体结构强度,伸缩臂主体材料采用Q460高强度钢,材料的弹性模量为210 GPa,泊松比为0.33,密度为7 850 kg/m3,屈服极限为460 MPa。
1)建立理论模型
伸缩臂截面如图3所示,图中的i=1、2,表示二节臂。伸缩臂整体受力如图4所示,截面对Z轴整体的惯性矩为
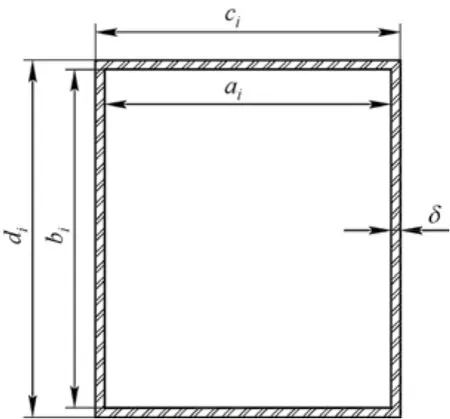
图3 臂截面图
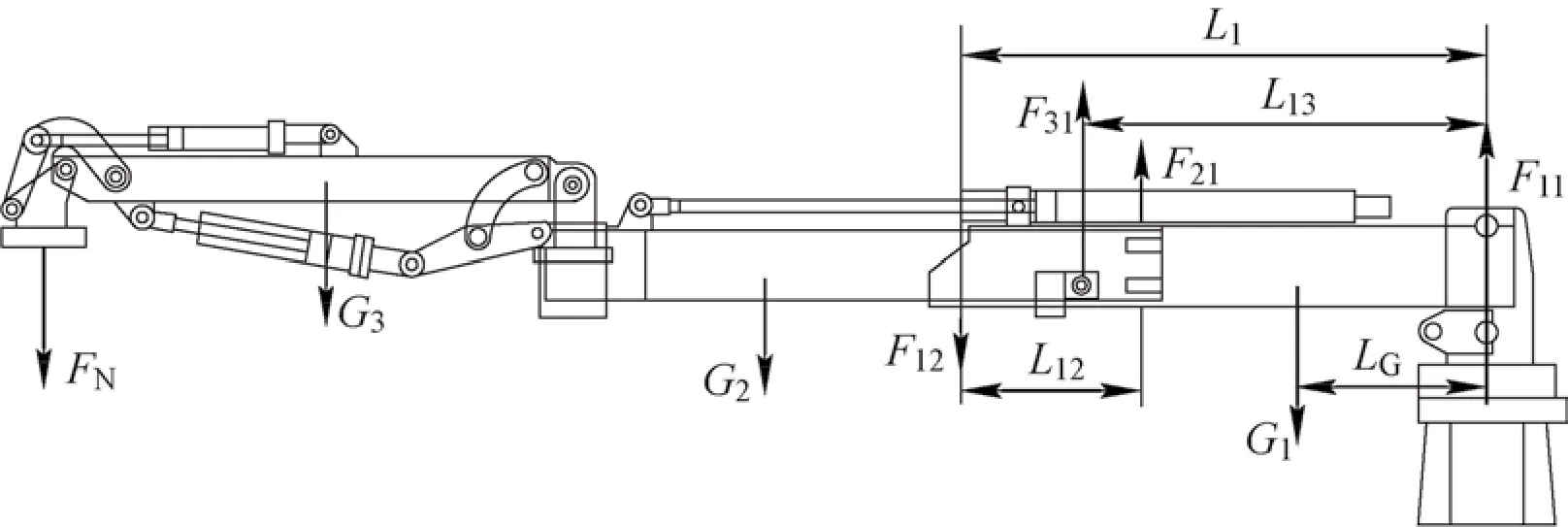
图4 伸缩臂整体受力图
式中:Ai为二节臂的截面,y为Y方向的坐标。
二级伸缩臂各截面关系图如图5所示,图中的ai、bi分别为滑块i的厚度、宽度,c1、c2分别为一节臂与二节臂的臂厚。
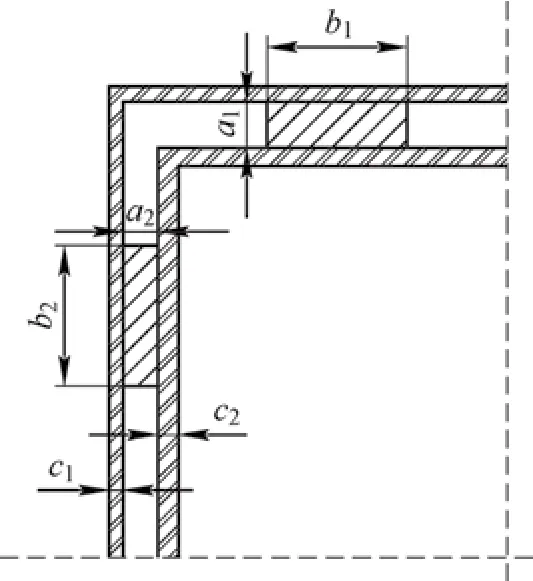
图5 截面关系图
2)确定二级伸缩臂的危险截面
对二级伸缩臂进行理论力学分析可得最大弯矩为
式中:F31为液压杆支撑力,F21为第2节臂对第1节臂的作用力,F12为第1节臂对第2节臂的作用力,L12为一节臂与二节臂重合长度,L1为第1节臂长度。
由此可见,伸缩臂的危险截面出现在第1节臂与第2节臂重合处,故对此危险截面处设计参数进行优化。
2.3 设计变量选定
选定伸缩臂危险截面各设计参数作为设计变量,即有
优化目标是使二级伸缩臂质量在条件允许范围内达到最小值,即
根据GB/T 3811—2008《起重机设计规范》分别设定优化约束条件,最大等效应力不超过许用应力,即δ=377 MPa;最大变形量不超过7 mm,故二级伸缩臂的多目标优化模型可表述为
式中:X为设计变量,f(x)为最大等效应力,l(x)为最大变形量。
3 二级伸缩臂响应面优化设计
3.1 构造响应面
为在极少试验下得到较高精度的响应面方程,现采用拉丁超立方设计(latin hypercube sampling)[11]来生成坐标点,如图6所示。
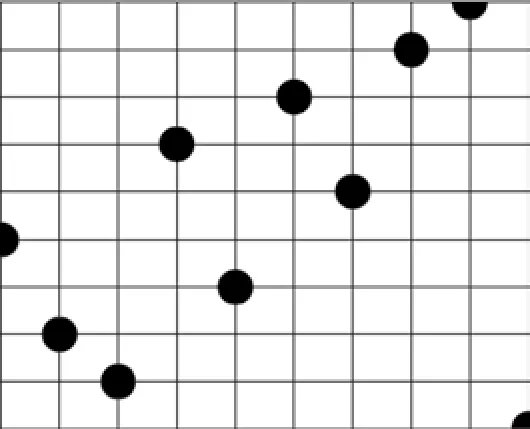
图6 随机拉丁超立方
在一个设计空间中抽取n个样本,每一个样本由m个分量组成,将每个分量的取值范围均分为n个,这样便可将这n个样本均匀地投放入设计空间内。当投放样本时,既要满足每一个样本点在小区间内均匀分布,也要满足所有样本点被投影到任意一维时每个区间样本点有且唯一。本方法与全因子设计法相比,在设计变量个数增加时,设计点数量并不会呈指数形式上升,抽样效率较高。
根据材料的特性参数,选取对二节伸缩机械臂影响最大的结构参数为设计变量,包括伸缩臂截面宽P1、伸缩臂截面长P2、板厚P3、上滑块厚P4、上滑块宽P5、侧滑块厚P6、侧滑块宽P7等。寻找这一设计变量组合对整体结构的影响趋势,即可求得响应面,实现对整体结构的优化。利用拉丁超立方设计方法针对这7个设计变量与3个响应设计了28组试验,试验方案与结果如表1所示。
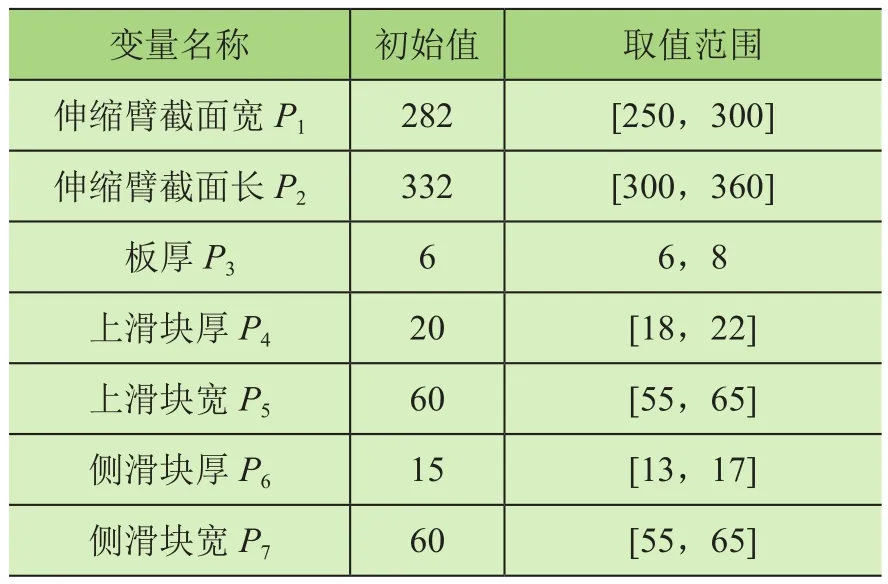
表1 设计变量及取值范围 mm
3.2 响应面预测能力准确性评估
由于复相关系数R2存在缺陷[12],即回归方程中自变量个数增加时,可能存在的冗余参数会提高R2的值,使得复相关系数无法准确预估回归方程的逼近程度,现采用修正的复相关系数R2adj来判断响应面的拟合程度,此时当参数个数增加时,R2adj不会随之增加。其计算公式为
式中:m为样本点矩阵的行数,k为参数个数,yi为响应值;i为响应估计值;为响应均值。
对表1试验设计点进行计算评估以确定函数拟合情况,计算结果如表2所示。
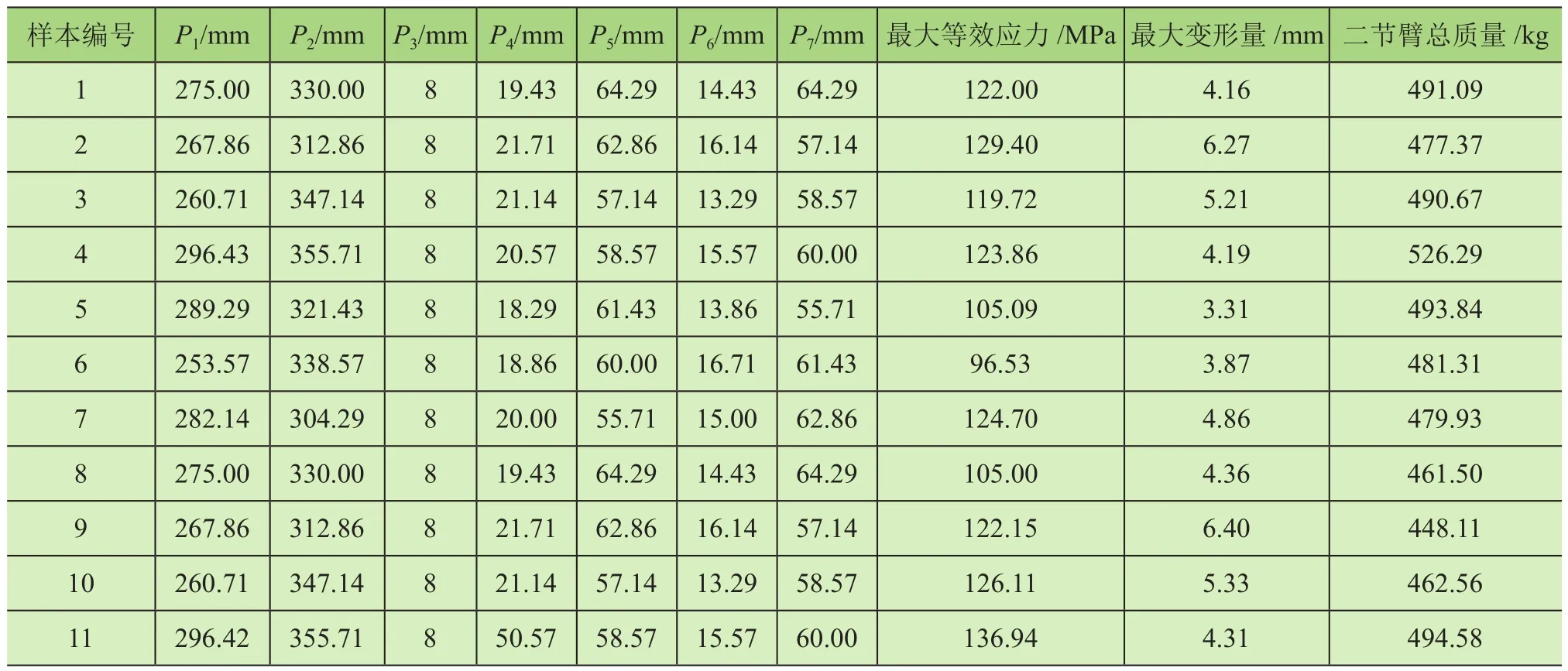
表2 拉丁超立方试验设计点
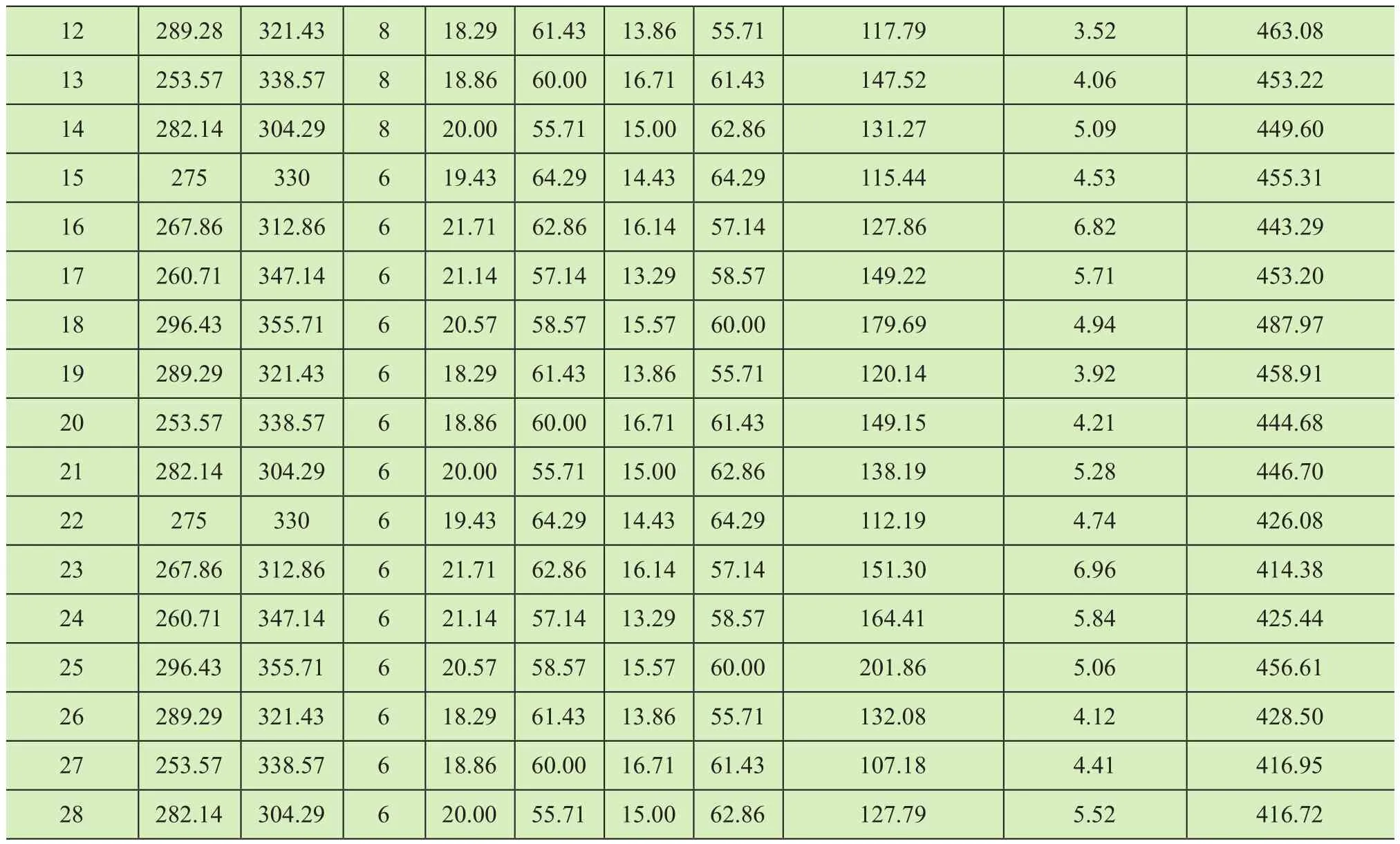
续接表2
由表3数据可知,3个目标函数的修正复相关系数分别为0.9989、1、1。由图7所示目标函数的响应面预测图可知,对于这3个目标函数,其预测值与计算值的关系曲线接近45°曲线,预测较为准确,与复相关系数吻合。本文中所有复相关修正系数均大于工程所需0.9的标准,且最大变形量与目标总质量的观测点可完全落在回归方程所确定的曲面上。由此可以看出,改进的响应面方法具有更好拟合水平,响应面可以较好地预测各设计变量的真实值,故可采用本响应面模型。
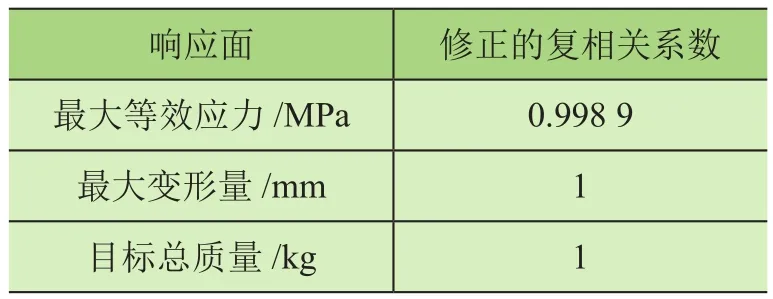
表3 响应面复相关系数分析
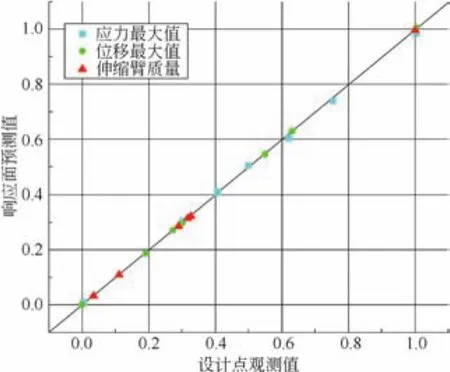
图7 目标函数响应面预测图
3.3 改进型RSM优化结果
采用多目标非支配排序遗传算法(NSGA-Ⅱ)求解式(9)所示响应面模型,可以得到多个Pareto解。
对于该机械臂的各目标优化中,各目标相互耦合,由此无法同时得到各目标的最优值。因此,需要对各优化目标进行判断权衡,以选取各目标的最佳平衡点,而表3所示的3组解在整个解域中为不同的优势解。
由于本次优化设计目标为质量轻量化,故选取候选点1为Pareto最优解。对候选点1进行圆整,以圆整后的值作为二级伸缩臂的最优设计点,对该参数下的机械臂受载情况进行仿真分析,得出如表4所示优化解。
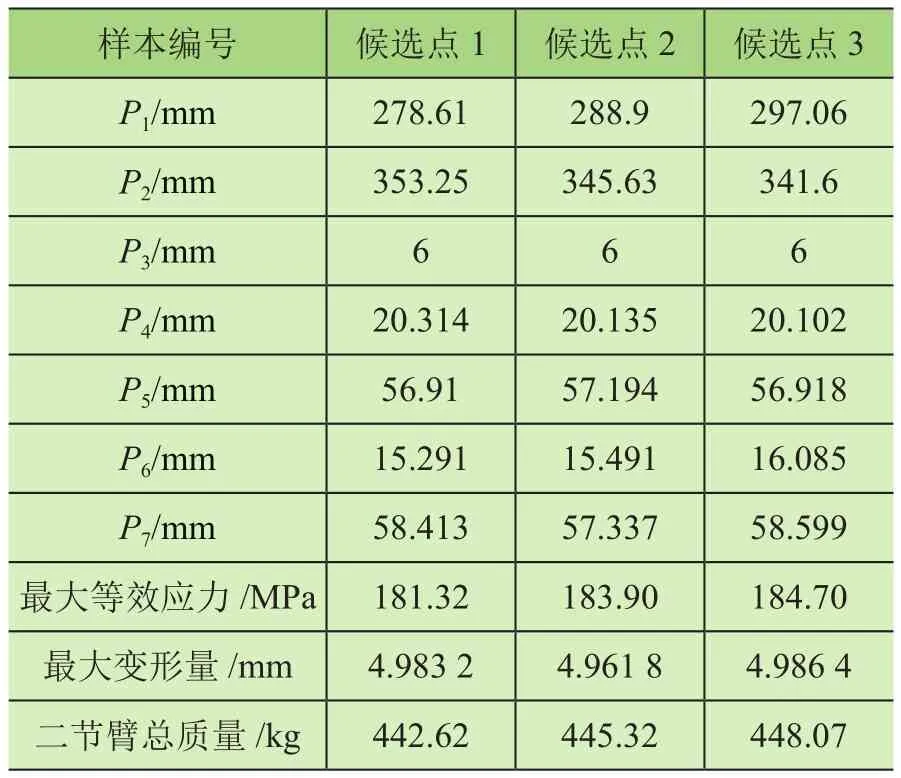
表4 Pareto候选解数据
对比优化前后的二级伸缩臂(见表5),响应面预测值与材料力学仿真分析值较为接近,表面响应面拟合隐函数精度较高;结构尺寸得到了优化,二级伸缩臂质量减轻了12.9%,伸缩臂最大应力与最大变形量均处于材料许用范围内。
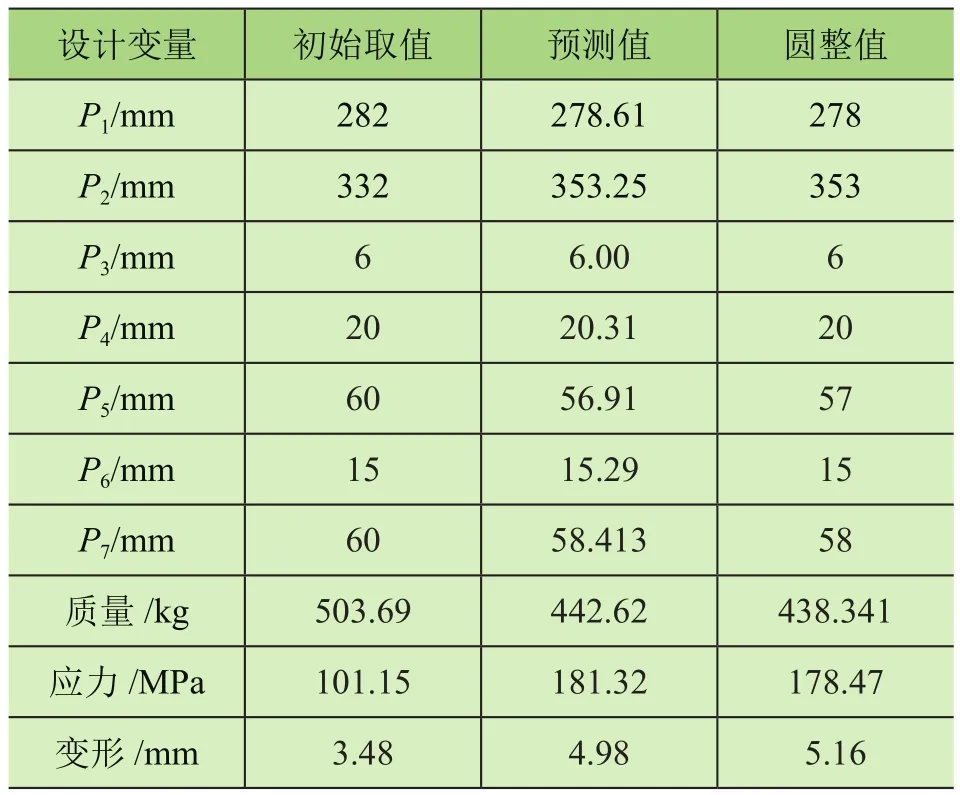
表5 优化前后对比
4 结论
1)利用基于中心展开点的响应面方法获得比传统响应面方法更精确的响应面拟合值,减少了多目标优化过程的优化时间。
2)采用拉丁超立方实验设计可以相对较少的实验数目设计完成较高精度的响应面模型,可在将各参数对模型力学参数影响的非显性关系可视化,为多目标优化问题提供更好地帮助。
3)运用改进型响应面方法与遗传算法相结合对二级伸缩臂系统的力学性能的优化效果较好,可用于二级伸缩臂部分板件厚度组合的确定。
