可重构闭链步行平台的设计与越障策略研究
2023-03-22姬佳璐姚燕安兰国荣
姬佳璐 姚燕安 张 英 兰国荣
1.北京交通大学机械与电子控制工程学院,北京,100044 2.杭州航天电子技术有限公司,杭州,310015
0 引言
足式机器人足端与地面离散接触,具有良好的地形适应能力,面对山地、丘陵等非结构化路面,可代替人类完成侦察、排爆、救援等艰难任务[1],在山地物资运输和灾难救援等领域具有广阔的应用前景[2]。
足式机器人腿部结构有开链式和闭链式。开链式腿机构移动平台具备突出的机动性能,如波士顿动力公司研发的BigDog[3]、SpotMini[4]和LS3,其中BigDog采用液压驱动,自重154 kg,负载50 kg,最快移动速度为11.16 km/h;SpotMini采用电驱动,自重30 kg,最大速度为5.76 km/h,可以负载14 kg进行奔跑。瑞士联邦理工学院研制的ANYmal[5]采用电驱动,自重30 kg,负载10 kg,腿部关节扭矩柔顺可控,对奔跑和跳跃时产生的冲击有很好的抵抗性。杨琨[6]研制了液压驱动四足机器人Scalf-Ⅲ,其自重200 kg且具有200 kg的负重能力,并提出了基于能耗最优的足端轨迹规划方法,实现了机器人的低能耗运动,但开链式移动机器人自由度多,增加了控制系统的复杂度。闭链式腿机构移动平台突出的特点是较少的自由度、简化的控制系统、良好的整体刚度以及较大的负载能力。PLECNIK等[7]研制的仿生跳跃机器人Salto,其腿机构为单自由度八杆连杆机构,在起跳过程中角动量近似为零,实现了稳定跳跃。KENNEALLY等[8]研制了Ghost Minitaur机器人,其腿部机构采用对心布置的平面五杆机构,有两个自由度,足端工作空间大,具有弹跳能力并且能够前翻和侧翻,运动较为灵活。张自强等[9-10]提出了多约束条件下闭链四杆腿机构的设计方法,考虑具有浮动机架、柔性胫骨和柔性关节的跳跃腿特点,提出了动态建模方法,为具有等效柔性胫骨和弹性关节的刚柔耦合四杆跳跃腿的设计和分析提供了理论依据;他们还以八杆仿生犰狳机构为例提出了一种构型与尺度同步设计方法,提高了单自由度机构的设计效率。单自由度闭链腿机构的平面运动特性限制了步行平台的灵活性,引入重构设计可有效提高其越障性能。FEDOROV等[11]设计了一种基于触发柔性元件的自适应机械腿,该机械腿将Hoecken四杆机构与缩放机构结合,在这些连杆上增加一个被动的第二自由度,在摆动阶段与障碍物碰撞后无需依赖任何传感器或特定的控制就可以对腿部进行机械重构,改变其传输和形状从而实现复杂地形障碍的穿越。武建昫等[12-15]基于杆长重构和躯干重构提出一系列可重构整体闭链多足平台,在越障策略方面做出了贡献。RUAN等[16]基于机架可变形的整体俯仰调节提出一种具有可调整变形机架的高越障性多足移动系统,俯仰调节可增大足端工作空间,并在纵坡攀爬时带来足端抓地优势。
鉴于单参数调节在兼顾提高越障能力与平顺性方面存在能力不足,本文以单腿机构最大纵向攀爬高度为重构调节目标,基于单腿机构跨步长、抬腿高度和质心波动值与杆长和倾角的关系,采用组合赋权法对杆长和倾角参数配比增益效果进行评估,设计双参数动力耦合的重构装置,构造双调节八足模块并建立越障概率模型计算平台的期望越障高度,提出双调节式全周期越障策略。
1 单腿机构运动学
本文研究的Watt型闭链腿机构如图1所示,为平面六杆七副机构,自由度为1。采用矢量环路法对该机构进行运动学分析,以曲柄的旋转中心为坐标原点O,建立坐标系OXY,图1中ri(i=0,1,…,9)为杆件矢量,θi(i=0,1,…,9)为杆件矢量ri与X轴的夹角。

图1 闭链腿机构简图Fig.1 Schematic diagram of the closed-chainleg mechanism
r0-r1-r2-r3和r5-r6-r7-r8两个矢量环路可由向量表示为
r0+r3-r2-r1=0
(1)
r5+r6+r8-r7=0
(2)
将式(1)与式(2)分别沿坐标轴分解,得到
r0cosθ0+r3cosθ3-r2cosθ2-r1cosθ1=0
(3)
r0sinθ0+r3sinθ3-r2sinθ2-r1sinθ1=0
(4)
r2cosθ2-r4cosθ4+r6cosθ6+r8cosθ8-r7cosθ7=0
(5)
r2sinθ2-r4sinθ4+r6sinθ6+r8sinθ8-r7sinθ7=0
(6)
求解得到中间参量θi(i=2,3,7,8)为
(7)
单腿机构的角速度ωi(i=2,3,7,8)和角加速度αi(i=2,3,7,8)可分别通过式(7)求一阶导数、二阶导数获得,求解过程中涉及的中间变量a、b、c用矩阵形式表示如下:
机构末端点f的位置可用矢量表示为
rf=r1+r2+r6+r9
(8)
2 双调节装置设计
2.1 参数调节特性分析
基于闭链腿机构运动学,对单腿机构进行尺度综合与优化设计,使其在一般行走状态下有一定的越障能力和行走平顺性。在MATLAB中建立机构末端点f位置坐标与杆长参数、倾角参数的函数关系,对应曲柄转动角度设定五个目标点进行逼近,采用序列二次规划法求解得到闭链单腿机构中连杆尺寸最优解,以该尺寸为单腿机构的初始尺寸,如表1所示,其中,r0~r9为杆长,θ2_4、θ3_6和θ8_9分别为r2与r4的夹角、r3与r6的夹角和r8与r9的夹角。

表1 闭链腿机构初始尺寸
评估步行平台越障能力的主要参数有抬腿高度、跨步长和质心波动值,其中抬腿高度越大,越有利于攀爬障碍,跨步长越大,整机推进能力越强,越障效率越高,质心波动值越小,平台越障过程越稳定。机架杆参数对足端轨迹特性主要参数的影响最明显,选择机架杆作为重构杆件,现以单腿机构最大纵向攀爬高度为重构调节目标,分别确定机架杆长r0与倾角参数θ0的调节范围。
(1)保持倾角参数θ0为37.5°不变,对杆长参数r0进行重构调节。依据曲柄存在条件以及足端轨迹封闭不交叉的原则,确定机架杆长取值范围为36.01~77.33 mm。以69.33 mm为初始值、3.33 mm为间隔改变杆长参数r0,图2为调节过程中的足端轨迹簇,图中红色曲线为减小杆长时的足端轨迹,蓝色曲线为增大杆长时的足端轨迹。图3为抬腿高度、质心波动值和跨步长与机架杆长关系曲线,杆长减小时抬腿高度与跨步长均增大,有利于障碍攀爬,但杆长过小时足端轨迹底部不光滑,影响行走平顺性,故确定以杆长减小为重构调节方向,并确定机架杆长调节范围为42.67~69.33 mm。

图2 调节杆长参数所得足端轨迹簇Fig.2 Foot trajectory clusters of rod length adjustment
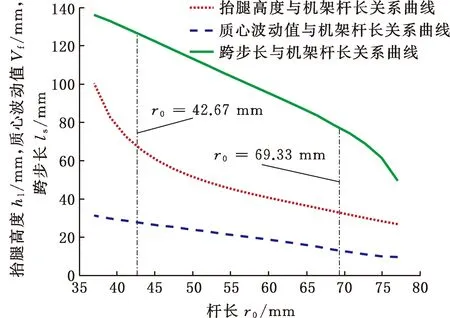
图3 抬腿高度、质心波动值和跨步长与杆长参数关系曲线Fig.3 Relation curves of leg raise height, centroidfluctuation and stride length with rod length parameters
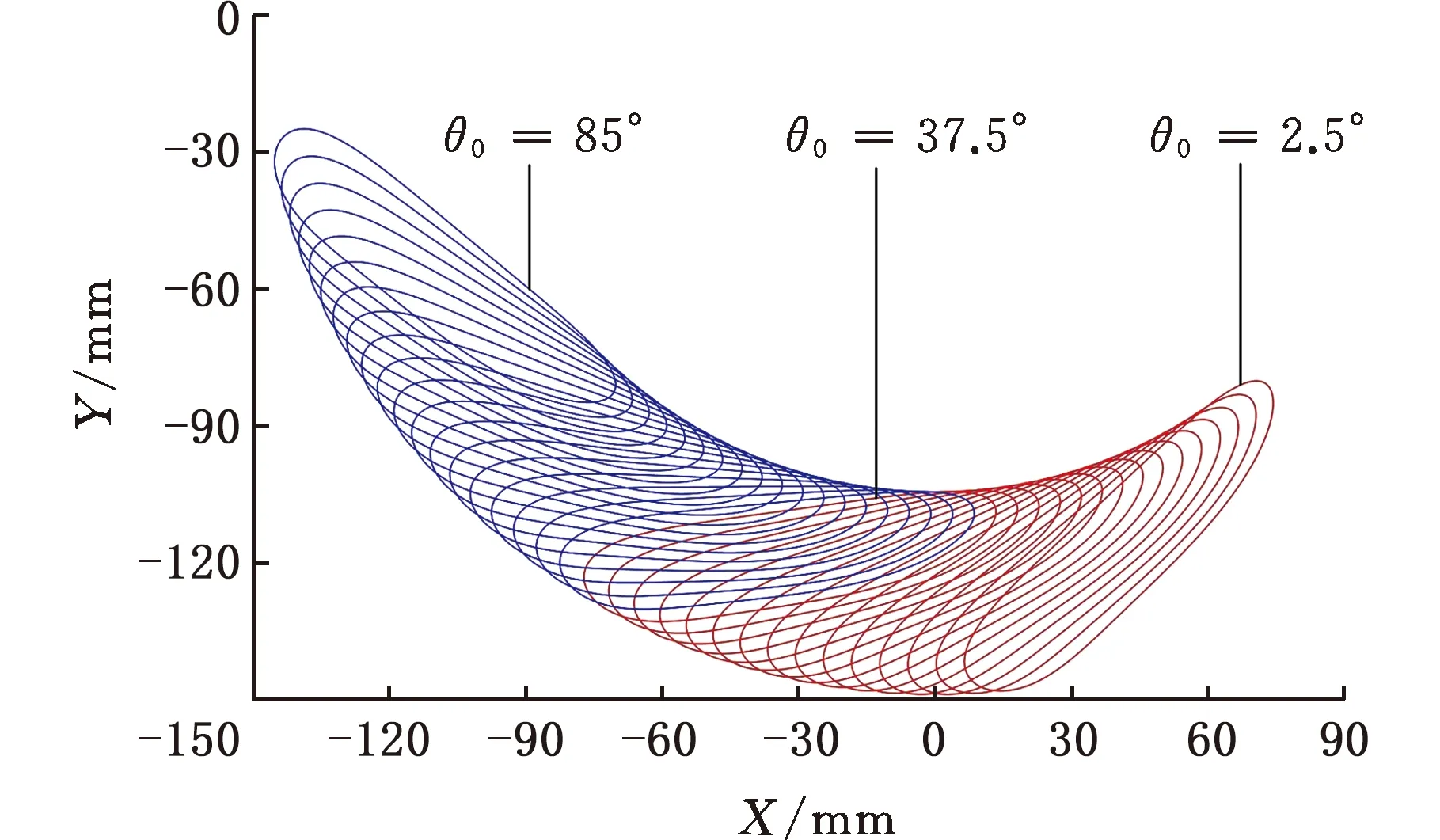
图4 调节倾角参数所得足端轨迹簇Fig.4 Foot trajectory clusters of inclination adjustment

图5 抬腿高度、质心波动值和跨步长与倾角参数关系曲线Fig.5 Relation curves of leg raise height, centroidfluctuation and stride length with inclination parameters
(2)保持杆长参数r0为69.33 mm不变,对倾角参数θ0进行重构调节。以37.5°为初始值、2.5°为间隔改变倾角参数,图4为调节过程中的足端轨迹簇,图中红色曲线为减小倾角时的足端轨迹,蓝色曲线为增大倾角时的足端轨迹。图5为抬腿高度、质心波动值和跨步长与倾角关系曲线,倾角增大或减小,质心波动值均增大;随着倾角增大,抬腿高度增大且足端轨迹向运动方向偏移,有利于障碍攀爬。随着倾角减小,抬腿高度增大但足端轨迹向运动反方向偏移,不利于障碍攀爬,故确定以倾角增大为重构调节方向,当倾角增大时跨步长先增大后减小,跨步长过小时步行平台越障过程中推进能力和越障效率急剧降低,故确定倾角调节范围为37.5°~72.5°。
在上述倾角与杆长参数调节范围内,提取足端轨迹特性参数,建立重构调节参数与足端特性参数之间的关系曲面,如图6所示。
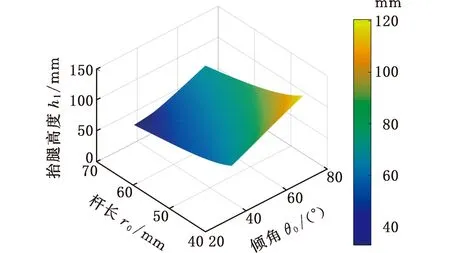
(a)抬腿高关系曲面
根据图6得到单参数调节与双参数调节的调节效果对比如表2所示,结果表明双参数重构调节相较于单参数调节,整机的越障能力大幅提高并能有效减小质心波动值、提高平顺性。
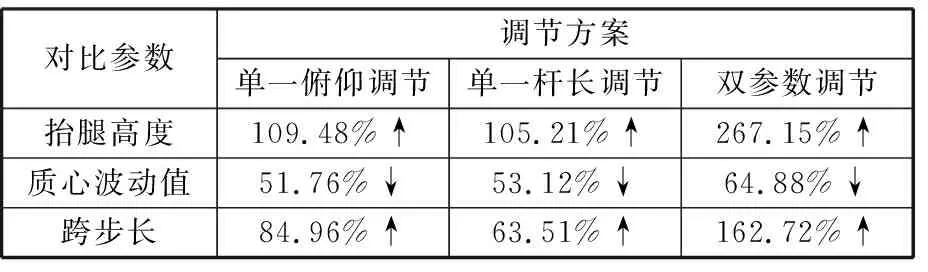
表2 调节效果对比
2.2 双调节装置设计
通过动力耦合设计,进行机架杆长与倾角参数的关联调节,保持单重构动力的同时兼顾越障能力与平顺性,以提高步行平台的可靠性。在熵权法[17]和变异系数法[18]的基础上,采用组合赋权法[19]进行机架杆长与倾角参数最佳重构配比评估。此次评估涉及3个指标分别为抬腿高度、波动值和跨步长,7个样本为机架杆倾角42.5°、47.5°、52.5°、57.5°、62.5°、67.5°和72.5°。
熵权法根据指标变异性的大小来确定客观权重,变异系数法利用指标样本值的差异程度来确定指标的权重[20]。构建足端轨迹特性参数评价指标体系,用组合赋权法开展特性参数评估。指定抬腿高度和跨步长为正向指标,数值越大越好,指定波动值为负向指标,数值越小越好,指定xij为第i个样本的第j个指标数值(i=1,2,…,n;j=1,2,…,m),n为样本总数,m为指标数。
对所有指标进行归一化处理,其中正向指标处理方法如下:
(9)
负向指标处理方法如下:
(10)
式(9)、式(10)中x′ij为标准化处理后的指标数值。
求解各样本占对应指标的比重pij:
(11)
求解指标熵值ej:
(12)
其中,k=1/lnn>0,满足ej>0。
求解信息熵差异dj:
dj=1-ejj=1,2,…,m
(13)
求解熵权法的各项指标权重wj:
(14)
(15)
求解变异系数法的各指标权重wi:
(16)
取两种评估方法对应指标的权重平均值再计算出其综合得分,具体结果见表3,其计算表达式如下:
(17)
i=1,2,…nj=1,2,…,m
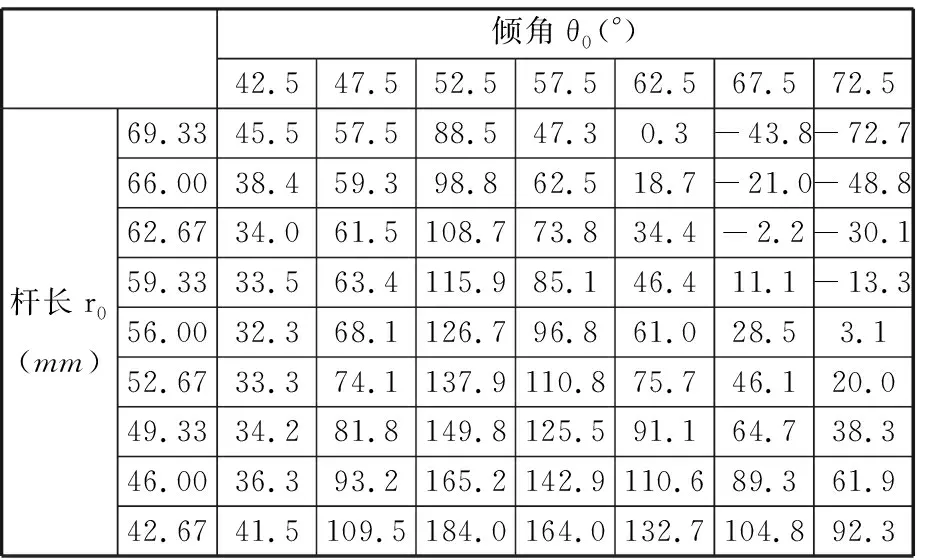
表3 综合得分
结合双调节关系曲面与组合赋权法的参数配比评估结果可知,当机架倾角增大时减小机架杆长可获得较大的抬腿高度与较高的综合得分,故设计腿机构倾角与杆长参数配比为72.5°与42.67 mm。
用转动导杆机构耦合杆长与倾角参数,设计出双调节装置,双调节重构示意图见图7。重构动力耦合过程为:驱动重构电机带动导轨机架相对固定机架AB转动,导轨机架带动导杆沿滑槽由C移动到C1,原机架杆AC重构后变为AC1,实现机架杆长与倾角参数关联调节。

图7 双调节重构示意图Fig.7 Schematic diagram of doubleadjustment reconstruction
3 越障期望与越障策略
3.1 越障期望
可重构闭链步行平台采用16足布局,两个闭链单腿机构共用机架构成双足行走单元,两个双足行走单元共用机架,双调节装置做对称布置形成四足行走模块,再将两个四足行走模块用车架连接构成双调节式八足模块,两个八足模块共用车架构成整机,共用机架可进一步减少步行平台所需的驱动电机数目。如图8所示,将八足模块沿行走方向划分为行走模块Ⅰ与行走模块Ⅱ,再将两个行走模块划分为跨越双腿Ⅰ、支撑双腿Ⅰ、跨越双腿Ⅱ和支撑双腿Ⅱ。
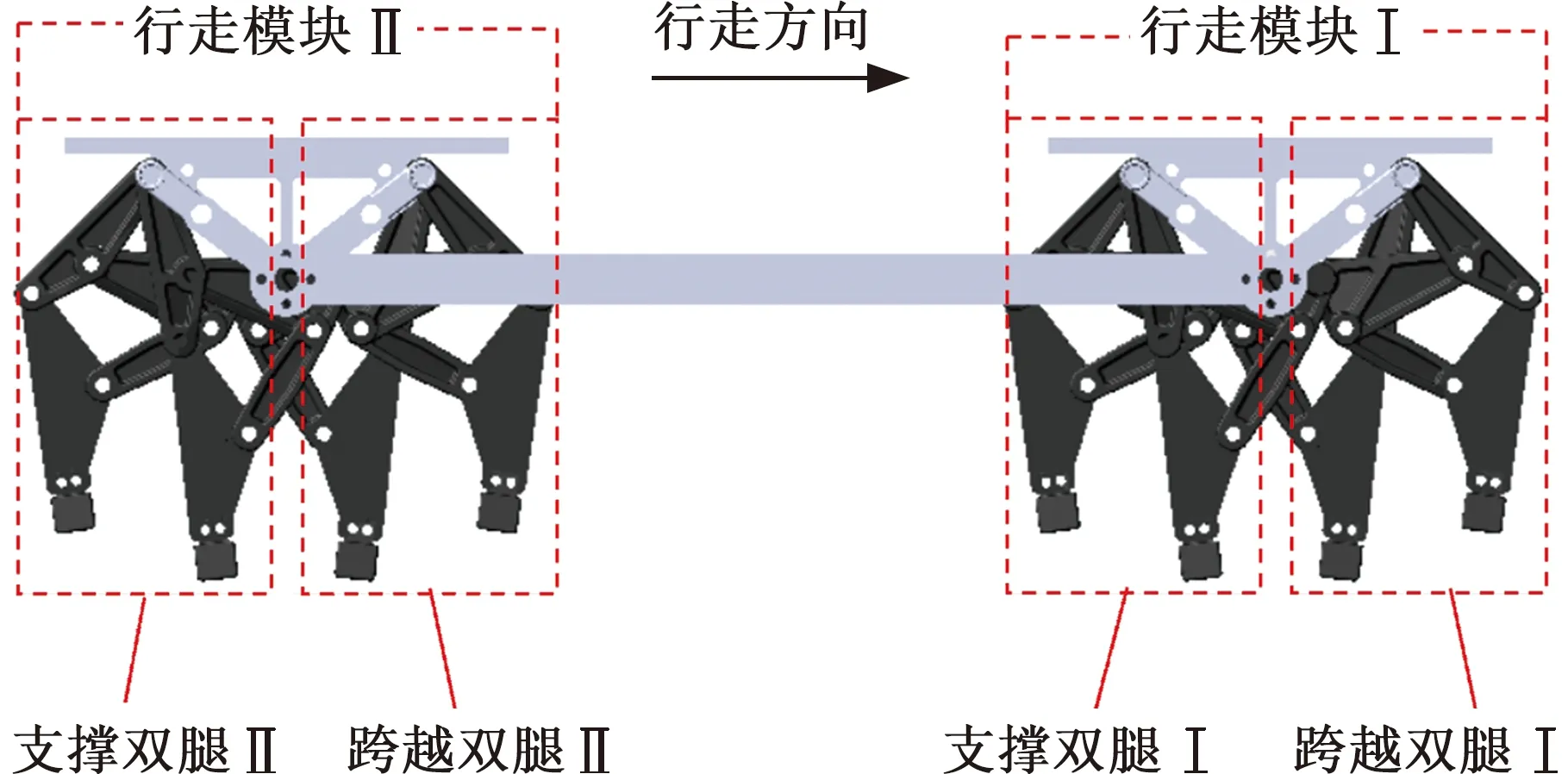
图8 双调节式八足模块Fig.8 Double adjustable octopodmodule
用ADAMS对双调节式八足模块进行行走仿真,单腿机构从足端离开地面到着地为一个行走周期,在一个行走周期内跨越腿的行走轨迹如图9所示,其中A、B为着地点,最大跨步高度H=88.2547 mm。

图9 双调节后的跨越腿行走轨迹Fig.9 Crossing leg track after double adjustment
根据行走过程中的支撑点切换,跨越双腿的着地点A、B之间为跨越区间,障碍落入跨越区间的位置具有随机性,当跨越曲线完全包含障碍且无交叉时,可实现成功跨越。在MATLAB中对跨越腿生成的行走轨迹进行三阶多项式拟合,坐标系中点A、B对应的横坐标分别为xA、xB,足端轨迹点纵坐标为y,拟合曲线结果如图10所示,得到的跨越轨迹拟合函数为
y=-2.557×10-5x3+0.013 33x2-
1.484x+276.7
(18)
求解式(18)反函数,可得
(19)
(20)
q=1.96×104h-5.62×106
对于高度满足h∈[0,H]的障碍,随机分布于[xA,xB],全闭链单元跨越双腿的越障概率为

图10 行走轨迹拟合Fig.10 Walking trajectory fitting
(21)
将障碍高度表示为h=H-y′,随机变量y′为越障裕量,可得到关于y′的分布函数,对其求导得到y′的概率密度函数f(y′)为
f(y′)=
(22)


越障裕量y′的期望为
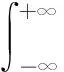
(23)
依据式(23)可得E(y′)=34.6765 mm,则越障期望E(h)=H-E(y′)=53.5782 mm。
3.2 越障策略
针对垂直墙、纵坡、壕沟及单边桥障碍提出双参数耦合调节的全周期越障策略,以高抬腿高度和足端与地面的高度贴合来实现平稳高效越障。
用ADAMS进行100 mm垂直墙障碍的攀爬仿真,根据两个行走模块分别踏上垂直墙障碍的顺序,将越障过程分为五个状态,如图11所示。障碍攀爬前整机状态如图11a所示,当行进至接近障碍时,驱动行走模块Ⅰ的重构电机,使其获得较大的抬腿高度,直到跨越双腿Ⅰ踏上障碍,整机状态如图11b所示;行走模块Ⅰ与行走模块Ⅱ存在高度差将迫使行走模块Ⅱ整体抬起,这不利于平稳越障,则驱动行走模块Ⅰ与行走模块Ⅱ的重构电机进行双调节,使足端与地面贴合,行走状态如图11c所示;行走模块Ⅱ接近障碍后,驱动行走模块Ⅱ的重构电机以相同的过程完成垂直墙障碍攀爬,行走状态如图11d、图11e所示。在越障过程中两行走模块的足端与地面接触更加紧密,提高了越障稳定性。

(a)状态1 (b)状态2
分别对30°纵坡障碍攀爬和40°纵坡障碍攀爬进行仿真,结果如图12、图13所示。行走模块Ⅰ与行走模块Ⅱ在接近障碍时通过双调节获得大的抬腿高度以进行攀爬,越障中及越障后通过双调节以调整足端与地面的贴合度从而保证平顺性,在坡面角度大于倾角调节范围的情况下依然具备突出的平稳越障能力。

(a)状态1 (b)状态2
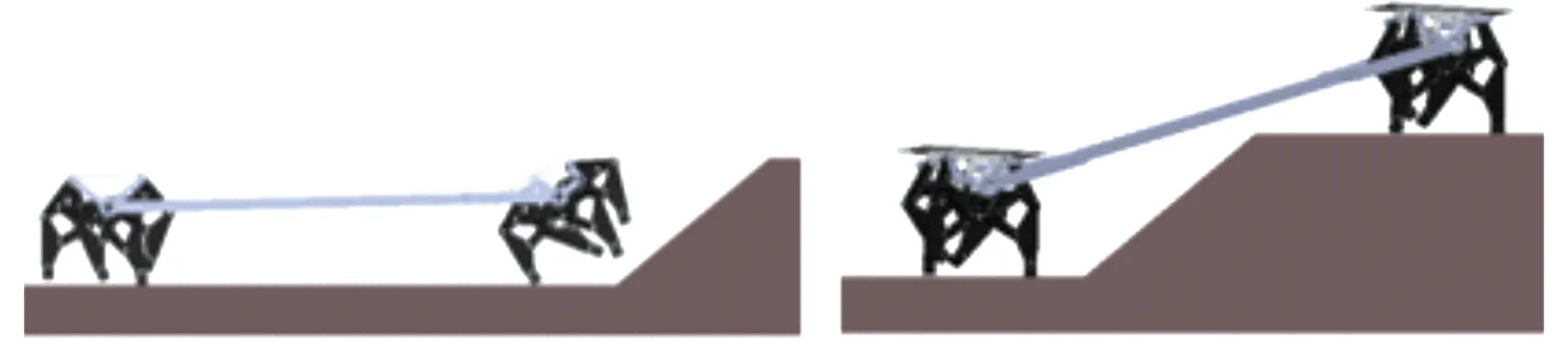
(a)状态1 (b)状态2
对宽度为100 mm、高度差为40 mm的壕沟进行仿真,如图14所示无调节平台无法跨过壕沟。双调节平台的越障过程如图15所示,平台接近壕沟边缘时状态如图15a所示,驱动行走模块Ⅰ的重构电机进行双参数调节,行走模块Ⅰ仰起后支撑双腿Ⅰ的相对跨步距离减小,能快速调节落脚点使其落在壕沟边缘,发挥最大越障效能,调节过程如图15b、图15c所示,跨越双腿Ⅰ跨过壕沟着地后,驱动重构电机使平台与地面贴合,如图15d、图15e所示。行走模块Ⅱ以相同的过程越过壕沟,如图15f~图15h所示。

图14 无调节平台的壕沟越障对比Fig.14 Trench crossing of platform without adjustment

(a)状态1 (b)状态2
在进行对称性地形障碍的越障时,两个八足模块工作状态完全相同,应对非对称性障碍时,两个八足模块独立工作。对于单边桥障碍,由于在跨上单边桥后各腿组存在较大的高度差,会造成某一个腿组悬空而导致平台倾翻,故无调节平台无法通过单边桥障碍。对16足双调节平台进行高度为40 mm的单边桥越障仿真,如图16所示,将越障过程分为4个状态。平台接近单边桥时,单边桥一侧的行走模块Ⅰ双调节后仰起,如图16a、图16b所示,行走模块Ⅰ跨上单边桥后调整其与地面贴合,同时单边桥一侧的行走模块Ⅱ双调节后仰起,平地上的行走模块Ⅰ双调节后俯下,重构足端轨迹后每一时刻下每个腿组均有腿足着地,保证稳定支撑与行进,平台状态如图16c所示,平台完全跨上单边桥后调整各行走模块与地面贴合,如图16d所示。
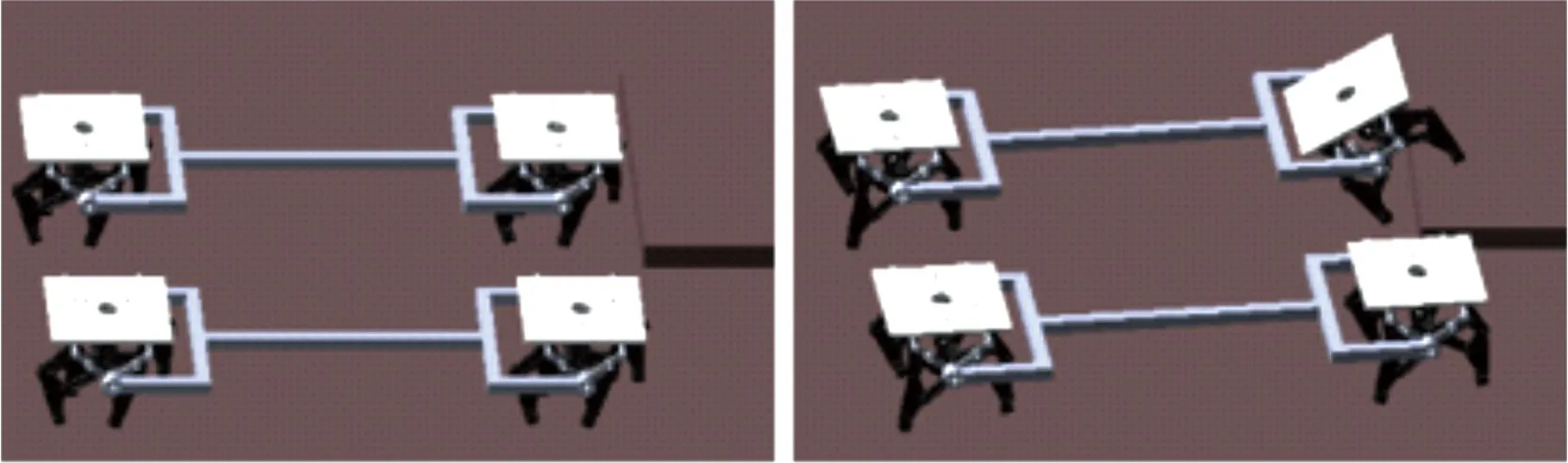
(a)状态1 (b)状态2
单边桥越障时整机的质心波动曲线见图17,可以看出,最大质心波动值仅为11 mm,表明越障过程平稳。

图17 单边桥越障时的质心波动曲线Fig.17 Fluctuation of center of mass in unilateral bridgeclimbing process
以30°纵坡越障为代表,双调节平台和单一俯仰调节平台(简称单调节平台)的参数对比如表4所示,表明双调节平台的质心波动值和越障所需功率均低于单调节平台,可降低能耗,并具有良好的平顺性。

表4 性能参数对比
基于双参数耦合调节的全周期越障策略,给出重构电机自主工作的判断方法。在越障过程中各足端受力情况反映了平台与地面的贴合程度,各行走模块与相邻两行走模块的相对高度反映了整机倾斜情况,当相对高度居中时,平台前后倾斜且左右倾斜,行走模块前方有障碍物时通过双调节越障,无障碍物时通过双调节调整平台倾斜情况,使平台与地面贴合,维持平台平稳行走。平台长度为L,行走模块长度为l,腿足与障碍物距离为X,判断流程如图18所示。
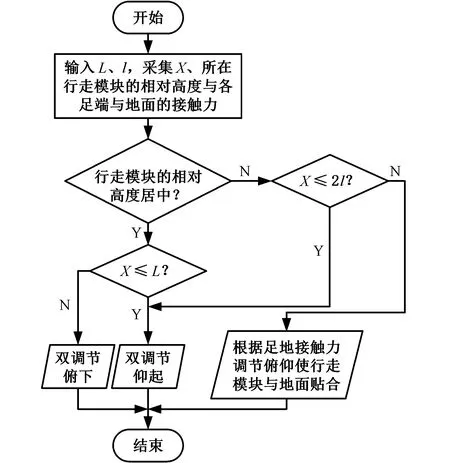
图18 判断流程图Fig.18 Judgment flow chart
综上,双调节平台利用全周期越障策略在应对大尺度垂直墙、纵坡、具有高度差的壕沟障碍时越障能力突出,以快速调节落脚点发挥越障效能,以增加平台与地面贴合度提高行驶平顺性,并通过调节腿足支撑实现了单边桥越障。
4 样机与实验
利用双参数耦合调节的尺寸参数对可重构闭链步行平台进行三维模型设计,加工装配得到的双调节式多足闭链平台如图19所示,样机参数如表5所示。

图19 可重构闭链步行平台样机Fig.19 Physical prototype of the reconstructionclose-chain walking platform
双调节式多足闭链平台采用4个行走电机和4个重构电机,行走电机分为左右两组,重构电机分为前后两组,平台的运动通过遥控器的两个通道向车载主控单元(包括STM32开发板、锂电池、接收机)发送运动指令,再由子控单元实现行走电机和重构电机的驱动控制,有序驱动4组电机完成整机的直行、转向和双调节攀爬越障。
对样机进行行走及越障试验。直行过程如图20所示。在道路上每间隔0.5 m做一个标记,操作样机沿直线方向前进,该试验中样机的空载行驶平均速度为51.1 mm/s,行走驱动电机转速为16 r/s,样机迈步频率为0.3 Hz。样机负载5 kg的行驶速度为45 mm/s,测量样机的质心波动值为14 mm。

表5 样机参数

(a)t=0 (b)t=20 s
图21所示为原地转向过程,控制一侧行走电机正转另一侧行走电机反转来实现差速转向,试验中转向速度约为2.25°/s。

(a)t=0 (b)t=20 s
图22所示为垂直墙攀爬试验。根据垂直墙攀爬策略,在闭链多足平台接近障碍时控制前面两个重构电机正转使前腿组仰起,前腿迈上垂直墙后控制前面的重构电机反转使前腿组与地面贴合,当后腿组接近障碍时进行相同操作,试验完成了80 mm的垂直墙平顺性越障,验证了双参数耦合调节设计的合理性与全周期性垂直墙攀爬策略的可行性。

(a)接近障碍 (b)双调节仰起
5 结论
(1)基于Watt型闭链单腿机构运动学分析了机架杆长和倾角参数与足端轨迹特性的关系,以高越障能力和行走平顺性为目标,采用组合赋权法进行双参数配比评估,设计出双调节装置。
(2)构造了双调节式八足模块,建立了越障期望概率模型并计算越障期望,制定了双调节下全周期障碍攀爬策略,仿真结果表明,双调节平台在应对大尺度纵坡、落差壕沟和单边桥障碍时具备出色的平顺越障能力。
(3)制作了一台样机进行直线、转向、垂直墙攀爬试验,实现了80 mm垂直墙障碍攀爬,验证了双参数耦合调节设计的正确性。
