基于协调影响流量的交叉口群主要流线识别

张建旭，吴成峰

（重庆交通大学交通运输学院，重庆 400074）

0 引 言

对交叉口群进行整体信号协调控制是当前交通发展形式下的重要课题，对交叉口群的主要流线（关键路径）进行干道信号控制是交叉口群协调控制的核心内容，而采用这一控制方式的前提是正确识别主要流线。

干道信号控制最早源于绿波带研究，美国的Little［1］最早创建了干道绿波控制模型MAXBAND 模型，但 该 模 型 应 用 难 度 较 大。Gartner 等 人［2］在MAXBAND 模型的基础上创建了MULTIBAND 模型，提高了模型的适用性，并且该模型是一个实时控制模型。这2 个模型也成为了干道信号控制的经典模型。Zhang 等人［3］进一步完善了MULTIBAND 模型，使模型适用于道路中心线不对称的情况。Yang 等人［4］扩大了研究范围，建立了多条路径的绿波协调模型。Abu-lebdeh 等人［5］研究当道路超出其通行能力时，利用模型优化信号配时，并剖析了道路双向信号配时模型的优缺点。于泉等人［6］提出了一种基于车辆队列长度的模糊逻辑规划方法，有效地减少了延误时间。傅惠等人［7］把最小延误时间和最大行驶速率当作优化目标，采取神经网络改善算法和群决策方法，创建了类似于双层规划算法的城市主干道信号配时优化办法。钱伟等人［8］提出一种以排队长度为优化目标的干道模糊协调控制方法。卫伟［9］也从车辆排队长度角度出发，加入了饱和状态下车辆油耗的问题，建立了多目标优化的协调模型，并利用现代智能优化算法进行求解。除此之外，还有很多学者对干线信号协调控制进行了深入的研究［10-13］。

目前大部分干线协调控制研究都集中在干线优化方法上，对研究对象，即主要流线的识别关注较少，大多以知道主要流线作为假设前提，或根据经验人工确定。工程应用中常用的路径识别及分级方法有浮动车扩样法［14］、视频检测法［15］、OD估算法［16］及数据挖掘法［17］等。根据城市道路的观测流量，利用OD 反推法也可以进行交叉口群路径估计［18-19］。针对OD反推法，Hu等人［20］对车辆检测器的布置策略进行了研究。Park等人［21］引入马尔可夫链对OD数据进行完善。程琳等人［22］运用随机用户均衡网络理论和网络要素选择，提出了交叉口分流率计算方法。卞建勇等人［23］提出了基于视觉和后推方法的智能车轨迹跟踪控制方法。李岩等人［24-25］根据交叉口群交通关联性强的特点，通过交通检测数据的短时变化特性，得出上下游流向的关联性，进而确定交叉口群的关键路径。卢慕洁［26］通过深度优先搜索算法，以交叉口之间的关联性为指标确定交叉口群的主要流线。Ma等人［27］认为当队列长度变得足以让队列的末端接近队列检测器时，从上游到达的车辆的速度将比自由流动速度慢，据此将关键路径识别的新标准分为可能拥塞的占用阈值和不可避免的拥塞的滚动时间占用数2个部分。

现有研究中，对交叉口群主要流线的识别主要通过分析各种交通检测器数据得到，这些数据多是离散的，难以反映交叉口群整体运行状态。上下游交叉口关联性能局部反映流量流向趋势，但不能准确刻画多交叉口路径的重要程度。基于全样车辆轨迹数据，能够得到准确的交叉口群主要流线，但利用当前的交通数据采集手段，难以获得全样数据。据此，本文假设路径受到协调控制，并分析协调影响流量的组成成分，结合浮动车数据和交叉口处的流量流向，建立交叉口群主要流线识别算法。

1 主要流线协调影响流量分析

主要流线是交叉口群进行协调控制的一个主要对象，主要流线的起点节点和终点节点都应该是交叉口群的边缘交叉路段端点，即主要流线贯穿交叉口群。同时，应包含2个及以上的交叉口节点。

在对交叉口群的主要流线进行交叉口信号协调控制时，总体协调控制效益取决于控制方案的合理性，以及受协调控制正面影响的流量，即协调影响流量。在控范围内的协调影响流量越大，协调控制的意义也就越大。

主要流线协调影响流量由多个部分组成，除了直接通过主要流线全程的车流外，中途汇入主要流线的一些车流也会受到协调控制的正面效益。

对图1中的交叉口节点和路段节点进行编号，圆形节点表示交叉口，线段端点表示路段节点。假设路径［5，1，2，3，4，10］为交叉口群一条主要流线的一个方向，对编号为1、2、3、4的交叉口节点进行主线协调控制。

图1 节点编号

受主要流线协调控制影响的流量主要有以下几种路径情况：

情况1 贯穿整条主要流线，受到协调影响交叉口节点数N=k-1，k为流量通过交叉口节点数。如图2所示，图中实线箭头表示协调影响路段，即在该路段的下游交叉口，车流能受到协调控制的效益，减少红灯等待时间。

图2 情况1

情况2 起始节点与主要流线相同，最后节点与主要流线不同，且连续通过主要流线交叉口节点数大于等于3，受到协调影响交叉口节点数N=k-2，如图3所示。

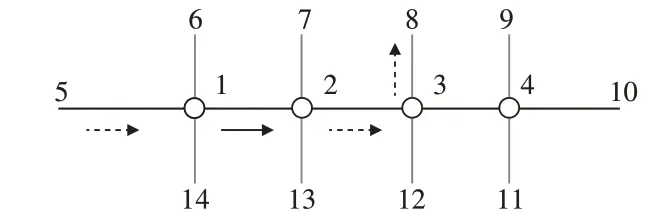
图3 情况2

情况3 起始节点与主要流线不同，最后节点与主要流线相同，且连续通过主要流线交叉口节点数大于等于3，受到协调影响交叉口节点数N=k-2，如图4所示。

图4 情况3

情况4 起始节点和最后节点均与主要流线不同，且连续通过主要流线交叉口数大于等于4，受到协调影响交叉口节点数N=k-3，如图5所示。

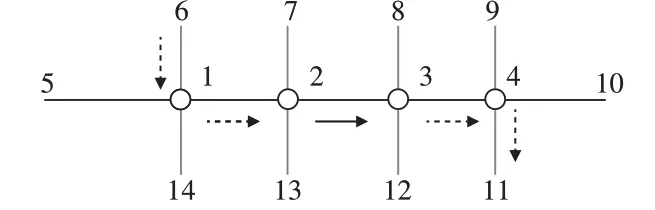
图5 情况4

除了上述4 种情况以外，其他与主要流线有交集的路径流量均不能受益于协调控制，减少交叉口处的红灯等待时间。将上述4 种情况的流量以协调影响交叉口数量的比例为权重，进行加权叠加，即可得到合理的交叉口协调影响流量。

2 交叉口群主要流线识别算法

2.1 基于轨迹数据的路径统计模型

浮动车的轨迹数据记录了浮动车行驶过程中位置与时间的变化关系，能够反映浮动车在路网中的行驶路线。对所有浮动车在交叉口群内路网中的行驶路径进行统计，分析不同路径上的浮动车数量，根据浮动车路径选择的特性，浮动车数量越多的路径就越可能是交叉群的主要流线。根据这一思路，建立基于浮动车数据的路径统计模型，以反映浮动车对路径的使用情况。

路径统计模型的算法设计步骤如下：

Step1 确定交叉口群中每个节点的数据采样范围半径，用来判断浮动车轨迹是否通过交叉口。当一辆浮动车在该范围内被采集到样本点时，则认为该浮动车通过这个节点。

Step2 选择一条浮动车轨迹Tri，遍历交叉口群中的所有节点范围，找出轨迹经过的所有节点。

Step3 提取轨迹经过的每一个节点中，最早采样节点的时间戳作为轨迹通过节点的时间，节点编号根据时间戳进行升序排列，即可得到该条轨迹的行驶路径LT=[d1，d2，…，dn]，dn为轨迹经过的第n个节点编号。路径提取过程中的数据结构示例如表1 所示，表中每一列数据为一条轨迹的通过节点时间和路径结果。

表1 浮动车路径提取表

Step4 对所有浮动车轨迹进行Step2和Step3。

Step5 筛选备选主要流线。

Step5.1 建立交叉口群边界节点编号集合Um。

Step5.2 建立备选主要流线集合Ub。

Step5.3 遍历所有轨迹路径LT，如果一条路径的第一个节点和最后一个节点均是交叉口群边界节点，即d1∈Um且dn∈Um，同时轨迹经过的交叉口节点数大于等于2，则该条路径为备选主要流线LT*，该条路径加入集合Ub。

Step6 统计集合Ub中不同主要流线出现的次数FLT*，i，作为第i种备选主要流线的初始协调影响浮动车数量。

Step7 修正备选主要流线的协调影响浮动车数量。

Step7.1 统计对应备选主要流线包含的各种子路径通过浮动车数量NLT。

Step7.2 选择一种备选主要流线LT*，进行协调影响浮动车数量修正，如式（1）所示：

式（1）中：F^LT*为修正后的备选主要流线浮动车流量；NLT，i、Ni分别为受该备选主要流线影响的第i种子路径的浮动车统计数量和该种路径的受协调影响交叉口节点数；N*为备选主要流线的协调影响交叉口节点数。

Step7.3 根据Step7.2 的方法依次计算所有备选主要流线的修正浮动车数量F^LT*。

2.2 基于流量转向比例的路径协调影响流量估计

在实际的交通数据采集过程中，只有完整获取路网中所有车辆的具体行驶路径才能统计出指定路径的实际流量。但这无疑是不现实的，现有的交通数据采集设施往往只有通过在交叉口处或路段上设置的摄像头对车牌进行提取，从而匹配出车辆的行驶路径，这样获取的数据通常会有很多缺失，难以接近全样程度。所以本文提出一种根据交叉口处各进口道的流量和转向比例对路径流量进行估计的方法。

对于一条假设的协调控制路径，从路径进口端的初始进入流量开始，每到一个交叉口节点，乘上交叉口沿路径方向的转向比例，直到路径结束，就可以得到估计的贯穿路径流量。该估计值为概率计算结果，虽然与实际的流量值有差异，但在路网层面具有与实际流量相近的分布比例，适用于刻画路径的流量水平。

除此之外，根据第1 章对协调影响流量的分析，还有很多交通量只利用了路径的部分路段。对于这些流量，按照浮动车路径统计模型的方法叠加到路径贯通流量上，估计得到路径协调影响流量F^。

路径协调流量估计模型的算法设计如下：

Step1 根据交叉口群节点转向关系和交叉口流向流量，建立节点流量转向关系数据表。如表2所示，表中T（a1，b1，c1）表示从节点a1出发，经过节点b1，到达节点c1的流量。

表2 节点流量转向关系数据表

Step2 建立相邻节点流量关系数据表。如表3所示，表中Q（a1，b1）表示从节点a1到节点b1的流量。

表3 相邻节点流量关系数据表

Step3 计算路径协调影响流量。协调控制路径及受协调影响子路径的贯通流量估计，如式（2）～式（5）所示。

其中：X为协调控制路径；xn为协调控制路径的第n个节点；Ri为在节点xi处，协调控制路径上游方向来的流量中，继续沿着协调控制路径下游而去的比例；fab为起点为a终点为b的路径从节点a汇入备选主要流线的流量；Fab为起点为a终点为b的路径的流量；xs为起点为a（a≠x1），终点为b的路径，与起点邻接的备选主要流线节点；Re为起点为a，终点为b（b≠xn）的路径，与终点邻接的协调控制路径节点处，从协调控制路径上游方向来的流量中，继续沿着协调控制路径下游而去的比例。

Step4 计算备选主要流线协调影响流量。备选主要流线下有许多由不同路段数量组成的子路径，同时对于包含同样数量路段的子路径也有多种可能。根据协调影响流量分析，备选主要流线的协调影响流量主要有4种情况，将几种情况进行加权累加得到F^，如式（6）所示：

其中：Fi j为第j个协调影响路段数量为i的子路径的基础流量；N为备选主要流线的协调影响交叉口数；W为协调影响交叉口数为i的子路径数量。

2.3 主要流线识别

一条路径的协调控制效益越高，则越可能是主要流线。路径协调影响流量F^ 和浮动车流量F^LT*均能反映路径在路网中的被利用程度，但各有不足。F^是根据转向概率估计得到的是一个理论计算值，由于司机的个人偏好和道路因素的变化，该值可能与实际情况有所偏差。F^LT*是根据实际浮动车数据统计得到的，能够真实反映路网中浮动车对不同路径的利用情况，但浮动车的渗透率是随时间和地点变化的，样本数量具有波动性。考虑到这些因素，本文对F^ 和F^LT*进行综合考虑，分别对2 种流量进行归一化后再叠加，作为备选主要流线的单向权重指标I1，I1∈[0，1]，如式（7）所示。

每一条主要流线，都会有一条与之相反的流线，信号协调控制也是双向同时协调，因此取双向流线的权重均值为整体权重指标，如式（8）所示：

其中：Ii为第i组备选主要流线的权重指标；Ii1、Ii2分别为第i组备选主要流线2个方向的权重指标。

根据权重指标I从大到小，结合交叉口群路网情况，选择合适数量的备选主要流线作为交叉口群的主要流线，以进行干线协调控制。

3 算例分析

案例区域为西安雁塔区的一个局部路网区域，如图6所示。

图6 案例区域

案例时段为17:00—19:00，根据交叉口关联度指标，在案例区域划分出一个交叉口群，图7 为交叉口群的拓扑结构图。浮动车数据来源于盖亚数据开放平台，流量数据如表4所示。

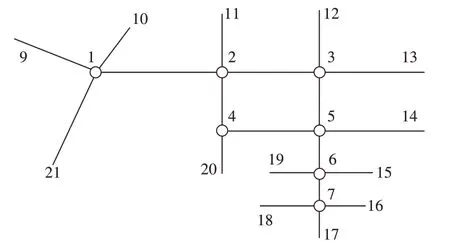
图7 交叉口群路网拓扑和节点编号

表4 各交叉口流向流量/（pcu/h）

根据2.1 节的浮动车路径统计模型，对目标交叉口群的备选主要流线进行识别筛选，并计算每条备选主要流线的双向协调影响浮动车数量。

再根据2.2 节的路径协调影响流量估计模型，计算出各个备选主要流线的双向协调影响流量，然后结合统计的协调影响浮动车数量计算各备选主要流线的协调效益权重指标，结果如表5所示。

表5 备选主要流线协调影响流量及权重排序

根据备选主要流线权重的排序情况，从高权重的备选主要流线开始依次选择交叉口群的主要流线，当后续的备选主要流线包含的交叉口完全与已选的某条主要流线相同时，则跳过该条备选主要流线，直到尽可能多地包含交叉口群中的交叉口。对于目标交叉口群，识别出3 条主要流线（双向），分别是［45，32，24，17，4，10］、［30，15，3，36］、［14，1，3，4，5］，如图8所示，与实际路网运行状况相符。

图8 主要流线识别结果

4 结束语

城市交叉口群动态优化控制是当前交通形式下的发展趋势，准确识别不同交通状态下的交叉口群主要流线是交叉口群干线协调控制得以实现的前提。本文从路径协调控制效益的角度出发，对路径的协调影响流量成分进行分析，在此基础上，通过短时浮动车轨迹数据找出可能是主要流线的路径，并结合流量数据计算路径在交叉口群中的协调效益权重，从而动态识别出交叉口群的主要流线。本文算法中仅使用了浮动车数据和检测的交叉口流量，基于协调控制效益的路径权重计算方法具有很好的扩展性，下一步可以尝试结合其他交通检测数据对算法效果进行改善，增加适用场景。