纠正学习策略下LightGBM-GRU模型的股票波动率预测
2023-03-21石志伟武志峰
石志伟,武志峰,张 哲
(天津职业技术师范大学信息技术工程学院(软件工程学院),天津 300222)
0 引 言
随着大数据时代的到来,社会各行各业都建立起了自己专业领域的大数据[1]。金融领域中指标的时间相关性尤为明显,非常具有研究的实际意义[2]。在众多金融指标中波动率是最具决策与指导意义的指标之一,它反映了价格的波动幅度,相对于未来的价格,人们更关注未来的市场趋势。精准预测波动率可以提高投资者的收益率,降低投资的不确定性,帮助从业人员进行风险管理、期权定价、资产配置,体现金融企业的行业软实力。虽然波动率的预测很有学术和实践意义,但是金融领域的数据具有高度非线性、高度复杂性、高度时间变化性等特点,使研究充满了挑战性,成为时间序列预测领域的难点[3]。
1959年Osborne[4]提出随机漫步理论,之后,1970年Fama[5]提出了有效市场假说,2位著名学者推断股票的相关指标无法被有效预测。但1999 年Lo 和Mackinlay 提出非随机漫步理论[6],证明了股票的相关指标通过有效的经济学模型可以被预测。随着预测模型的不断优化,在金融界产生了量化投资的全新投资方式,它以统计、分析、预测的客观结果进行投资。传统投资方式是凭借人们的主观判断进行决策的投资。1971 年美国巴克莱投资管理公司发行了首只量化投资策略的基金[7]。美国的量化交易占比超过70%,中国起步晚10 年以上,目前占比超过20%,正处于高速成长阶段。
在过去的研究中,对于时间序列以及波动率预测,不同的学者和专家给出了自己的解决方案。最初,在经济学领域,1982年Engle[8]提出的自回归条件异方差(ARCH)模型和1986年Bollerslev[9]提出的广义自回归条件异方差(GARCH)模型都被成功应用于波动率的时间序列预测。
随着人工智能的兴起,机器学习开始被应用到各个行业来解决工程难题。2017 年,Liu 等人[10]使用回归树模型成功预测了铜的长短期价格。人工神经网络与深度学习框架是近年来人工智能研究领域的热点。1988 年,White[11]使用人工神经网络成功预测了IBM 股票的日常波动率。然而,金融大数据强随机性和动态非线性的特点,使得普通神经网络的拟合度较差,1997 年,Hochreiter 等人[12]提出能够存储时间信息的长短记忆神经网络(LSTM)。2015 年,Chen 等人[13]通过LSTM 模型成功预测了中国股市的收益率。2017 年,Nelson 等人[14]使用LSTM 模型成功预测了股市的波动率。随着学者们的深入研究,周志华老师提出了集成学习策略。2016年,Khaidem等人[15]使用随机森林模型有效预测了股票收益率。2019 年,Basak等人[16]使用GBDT 模型成功预测了股票波动率,GBDT 也成为了当前在金融领域进行时间序列预测的首选建模方式。
虽然众多学者的研究已经取得了很多的成果,但是本文发现其还存在很多问题有待解决:
1)即使是目前效果最显著的集成学习的方式,在误差方面也存在一定的缺陷:Boosting 的集成策略可以降低偏差但对方差没有效果;Bagging 的集成方式可以降低方差但对偏差没有效果,表现在工程应用中就是模型预测的精确度和泛化能力(结果可信任度)无法得到兼顾。
2)对于目前比较热门的神经网络和深度学习来说,如果用它直接训练模型,模型的可解释性差,所消耗的时间与计算资源也是巨大的,随着输入特征值的数量增加,模型的维度、复杂性、不确定性都是不可控的。
3)人工智能到来之前,智能算法的矛盾为算法匮乏与用户对算法需求日益增长之间的矛盾。在当前人工智能-大数据环境下,智能算法的矛盾转变为算法通用性有限与工程问题多样性之间的矛盾。虽然现在是一个算法富集的时代,但是没有完美的算法,没有普适的模型,面对各类数据问题怎样才能提高现有智能算法的适应能力呢?
针对上述问题,本文提出纠正学习的策略:根据不同的工程数据,选用传统的机器学习器进行学习,将学习结果通过纠正学习器进行学习纠正,不仅能够同时提高传统学习器的预测精度和泛化能力,也能够提高传统学习器的适应能力。为了验证纠正学习的效果,本文以股票波动率预测问题为例进行仿真。学术界普遍认为通过集成学习训练的模型是一种比经典的效果更好的算法,为了更有力地说明纠正学习的效果,本文选择LightGBM 作为基础学习器,GRU神经网络(Gated Recurrent Unit)作为学习纠正器,形成LightGBM-GRU 混合模型。
本文的主要工作如下:
1)提出当前智能算法存在的矛盾:智能算法通用性有限与工程问题多样性之间的矛盾。
2)指出当前时间序列预测研究存在的问题,提出纠正学习策略,使用训练LightGBM-GRU 模型来预测126 只不同行业的股票波动率,得到的预测结果比LightGBM有更低的误差率和更高的泛化能力。
3)以GRU作为纠正器,既保留了该模型对时间序列预测的优势,又避免了深度学习框架直接进行训练的高消耗与不稳定性,为深度学习提供了降维思路。
4)给出了纠正学习策略能够成功的理论分析,证实纠正学习策略的可用性与可研究性,提出纠正学习策略能够提高现有智能算法对各类工程问题适应性的观点。
1 方 法
1.1 LightGBM
在1990 年,Schapire[17]提出并论证了Boosting 集成学习算法的提升效果。LightGBM(Light Gradient Boosting Machine)是目前用于时间序列预测中精度最高的算法。
步骤1 初始化CART学习器。
步骤2 对于迭代次数t=1,2,…,T:
1)对每个样本i=1,2,…,m,计算t次迭代的负梯度(残差)。
2)将上一步得到的残差作为样本数据的目标值,将(xi,rti)(i=i,2,…,m)作为第t棵树的训练数据,拟合新的回归树ht(x),该树对应的叶子节点区域为Rtj(j=1,2,…,J)。其中J为回归树叶子节点的个数。
3)损失函数最小的情况下,估计出相应叶子节点区域Rtj(j=1,2,…,J)的值。
4)更新学习器。
步骤3 得到最终学习器模型。
1.2 GRU
1990 年Elman[18]提出循环神经网络(RNN,Recurrent Neural Network)。
图1为RNN结构图:X表示输入层的值;S表示隐藏层的值,其节点个数与向量S的维度相同;O表示输出层的值,U是输入层到隐藏层的权重矩阵,V是隐藏层到输出层的权重矩阵。

图1 RNN算法描述及其时间展开图
RNN的计算公式如下:
其中g(·)、f(·)为激活函数。
为了克服RNN 在训练中很容易发生梯度爆炸和梯度消失的缺点,Junyoung Chung 等人在2014 年提出了GRU(Gated Recurrent Unit)[19]。图2 为GRU 计算示意图。

图2 GRU计算示意图
GRU的前向计算公式为:
其中“◦”表示哈达马积(Hadamard Product),即对应位置相乘。
1.3 纠正学习
1.3.1 算法描述
前文引用的大量文献表明,不同的回归模型算法对不同的数据有着各自的适应性。本文提出一种纠正学习算法,以神经网络作为模型纠正器,传统的机器学习模型作为基模型,通过纠正学习来降低模型的偏差与方差。具体实现方法是将基模型的输出作为纠正器的输入进行训练与预测。纠正学习的策略可以针对不同的数据或业务需求选用不同的基模型与纠正器,纠正学习策略具有一种算法上的相对普适性。纠正学习的目的是让基模型的学习结果更加接近真实值,并且提高模型对不同工程数据的适应性。公式描述如下:
其中,f为基模型,O为基模型的输出值,h为纠正学习器,Y为进行纠正学习后的输出。
1.3.2 理论分析
纠正学习是选用基础学习器进行学习,将学习结果通过纠正器进行纠正的策略。基础学习器和纠正器可以根据数据特点灵活选择机器学习模型,但是基础学习器和纠正器应该为不同的模型。基础学习器通过数据集完成训练和建模,纠正器在同一个数据集的基础上,根据基础学习器的输出结果和真实的目标值完成训练和建模。不同机器学习模型训练出来的学习器具有不同的偏好,纠正学习策略是在基础学习器的基础上根据真实值进一步学习和拟合,这可以从直觉上解释为何纠正学习策略能够成功。
具有不同偏好的学习器可以给样本不同的标记,如纠正器中应该能够学习到一些基础学习器不具有的信息,即基础学习器不能正确标记的样本可能会被纠正器正确标记。如果基础学习器和纠正器具有较大差异性,那么使用纠正学习策略可能会取得更好的效果,因此2 个学习器具有较大的差异性有可能是使纠正学习策略成功的条件。
论证:
A、B分别表示基础学习器和纠正器。d(A、B)表示学习器A、B之间的差异性。eA表示A的误差率,eB表示B的误差率。存在以下不等式:
纠正器的选择是多种多样的,本文实验中的纠正器选用的是神经网络。神经网络是通过足够多的简单转换函数及其各种组合方式来学习的一个复杂的目标函数,可以用以下简单方式表达:
对于同一个样本X,B学习器会根据目标值对A学习器得到的结果YA(X)进一步拟合,最终由纠正器产出的YB(X)结果会更加接近于真实值。
当d(A、B)越大时,学习器A与学习器B对样本X标记的不一致性越大,学习器A学到的信息与学习器B学到的信息差别越大,B对A贡献的信息越不相同,B能纠正A的可能性也就越强,B以寻优的学习原则进行学习时,可以得到:
通过以上推导基础学习器和纠正器的差异性是纠正学习策略成功的充分条件,即基础学习器和纠正器只要具有差异性就可以通过纠正学习策略提高整体的精确度。在训练过程中基础学习器和纠正器之间呈现一种相互扶持的态势。
1.3.3 LightGBM-GRU
为了证明纠正学习策略的正确性,本文选用金融数据这一时间序列预测中的难点进行实验,并且基础学习器选用学者们认为经典的效果比较好的集成学习模型。针对股票波动率预测这一具体问题,设计如图3 所示的混合学习模型,该模型命名为LightGBMGRU。LightGBM-GRU 是以GRU 为纠正器,Light-GBM为基础学习器。
算法1 给出了波动率预测中纠正学习算法的详细步骤,图3 详细展示了所提出的LightGBM-GRU 模型架构图。

算法1 纠正学习算法LightGBM-GRU输入: 历史的股票交易数据(划分训练集与测试集)。输出: 未来的股票波动率。# 建模步骤1: 将训练数据集LightBoost 进行建模,通过调参训练,让模型达到最优的学习状态。步骤2: 将训练集输入到训练好的LightBoost模型,模型的输出结果以及目标值(真实的波动率)作为GRU的输入进行建模,对GRU进行调参训练。# 预测步骤3: 将测试数据集输入LightBoost进行预测。步骤4: 将LightBoost 的预测结果作为GRU 的输入得到最终的预测。
选择GRU 作为纠正学习器的优势如下:神经网络是一种低偏差、高方差的模型,属于一种不稳定的学习器。面对高维度、动态随机的金融大数据,神经网络如果直接做预测模型,则存在耗时、耗资源、超参难调、稳定性差、解释性差(黑盒算法)等缺点。用基于学习器的预测结果作为输入,用GRU 深度学习框架作为纠正器进一步拟合回归,得到最终的混合模型,为深度学习提供了一种降维的操作。这样能避免直接用神经网络预测的缺点。用神经网络自主适应、自主学习、快速拟合、快速寻优的优点去寻找混合模型方差与偏差的最优平衡点,使得模型的可解释性、稳定性、精确度、泛化能力都能达到相对最优。
2 仿真实验
图4和实验步骤1为进行股票波动率预测仿真的整体思路与步骤描述。

图4 实验步骤图

实验步骤1实验步骤 股票波动率预测输入: 历史的股票交易数据。输出: 未来的股票波动率。#数据预处理步骤1 数据描述:了解数据集的数据结构,进行数据清理、缺失值处理、数据标准化,划分训练集与测试集。步骤2 数据探索性分析:探索数据集的整体分布,为特征工程与建模参数设置进行准备。步骤3 特征工程:根据步骤2,从数据的角度对数据集进行特征工程与向量编码。#建模与训练步骤4 分别对LightGBM-GRU 进行建模训练以及参数调优。#模型评估步骤5 选用多种实验中需要的评估模型。如果模型训练无法回归,则重新调整特征工程;如果模型回归后误差太高,则重新调整模型参数后训练。#实验结果与分析步骤6 对所有模型的预测结果进行分析,说明纠正学习策略的价值。
2.1 数据预处理
2.1.1 数据描述
仿真数据集来源于Optiver 对外提供的数亿条细化的历史金融数据,数据拥有以秒为单位的时间精度,这些数据来自不同行业的126 只股票近3 年的交易历史。数据集的多样性与差异性更能全面、真实地评价所提模型的有效性和实用性。实验所用数据集的数据结构如表1所示。

表1 数据集结构
本文的研究目标是以历史10 min 内的股票交易数据来预测未来10 min的股票波动率。将st称为股票S在时间t的价格,t1和t2之间的对数收益公式定义为:
10 min固定时间窗口的对数收益率可表示如下:
计算所有连续账簿更新的对数收益率,对数收益率平方和的平方根则为波动率的定义[20]。公式如下:
由于各因子的量纲不同,需将数据进行归一化处理,然后将数据按照8:2的比例划分训练集和测试集,为了保证所得模型的可靠性,相对训练集来说,测试集数据皆为未来时间段的数据。
2.1.2 数据探索性分析
图5 为训练集数据中时间窗口的数据长度分布(以股票ID 为0 的数据为例):一个10 min 的时间窗口包含600 s 的时间点,每只股票的不同时间窗口的数据量不相同,且成正态分布,大部分时间窗口的数据量小于600,所以数据是不连续的,数据段seconds_in_bucket 隐含了股票的活跃度信息,可以为特征工程提供启发。

图5 时间窗口的数据量分布图

图6 波动率分布
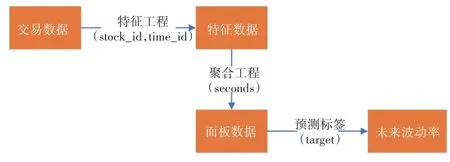
图7 特征工程流程图
2.2 建模与训练
2.2.1 实验环境
仿真环境以及模型的训练预测环境都是Python3.X。实验运行平台为:AMD Ryzen 9 5900HX,NVIDIA GeForce RTX 3080,32.00 GB installed RAM。
2.2.2 模型参数设置
仿真采用的纠正器为图8 所示的多层神经网络:第1 层为由100 个神经元组成的GRU 层;第2 层为由10 个神经元组成的GRU 层;第3 层为Dense 全连接层。为了减少过拟合现象,提高纠正器的泛化能力,前2 层在每层之后都会使用Dropout(0.2)方法,即训练过程中,神经元按照20%的概率暂时丢弃。具体参数设置见表2。仿真采用的基础模型LightGBM 的参数设置见表3。

表3 LightGBM 参数设置表

图8 GRU神经网络图

表2 GRU参数描述表
2.3 模型预测评估
在评估和分析一个模型的性能与预测能力时,采用多种不同的评价指标是很重要的[21]。本文采用MSE(预测模型最通用的度量)、MAE(注重测试离群点误差)、RMSPE(解决鲁棒性问题)、RMSE(避免出现量纲问题)作为评价指标。其中MAE 为平均绝对误差、MSE 为均方误差、RMSE 为均方根误差、RMSPE为根均方百分比误差。具体公式如下:
其中,σt为时间窗口t时的波动率真实值,σ^t为时间窗口t时的波动率预测值。因此上述评估标准的值越小,则表明模型预测的精度越高。
2.4 实证结果与分析
图9 给出了不同模型在测试集上的预测结果与真实值,为了便于展示与观察,图中数据为随机抽取的20个预测点。观察图9不难发现,不论是准确度还是稳定性,LightGBM-GRU 模型的预测效果都是最好的。虽然不同行业不同股票不同时间段的波动率变化是不同的,但纠正模型的预测结果更接近真实值。由于图9 所示真实波动率具有非线性、非平稳性、突变性等特点,因此集成学习成为了目前主流的预测算法,学者们也普遍认为集成学习是一种经典的效果比较好的算法[22],但仿真结果表明了纠正学习策略能够进一步提升集成学习的性能。
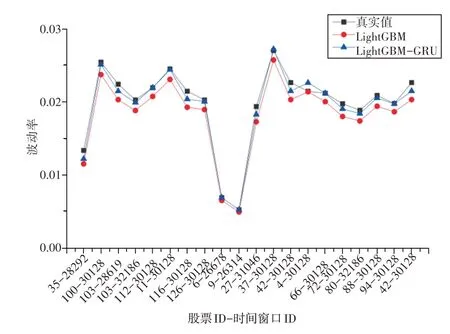
图9 股票波动率预测结果对比图
为了定量分析预测结果,图10和表4列出了不同评价指标对上述不同模型的评价结果,LightGBMGRU 的数值都小于LightGBM,即纠正学习模型在所有情况下都优于传统模型。这是由于股票价格的原始信号波动频率高,突变幅度大,直接使用传统模型很难提取和分析其变化规律,通常很难得到满意的预测结果[23]。对原始信号进行纠正学习后,输出的回归结果更稳定,减少了原始数据中不同尺度特征信息之间的干扰和耦合,更容易获得原始序列复杂的内部特征,包括线性和非线性特征,从而减轻了模型的负担和预测的难度。因此,与单模型方法相比,纠正学习模型的预测性能有很大的提高,对纠正学习模型来说,基础模型和纠正器对最终的预测结果具有相互促进的作用。

图10 模型误差对比图

表4 模型评估对比表(基于测试集)
偏差描述的是预测值的期望与真实值之间的差距,偏差越大,越偏离真实数据,反映了模型的预测精度[24]。方差描述的是预测值的变化范围、离散程度,也就是模型在训练集与测试集的效果差异度,反映了模型的泛化能力[25]。结合表5 和图11 可以观察到所有的模型在训练集和测试集上,模型预测误差都存在偏量。这些偏量影响了人们对模型效果的可信度。LightGBM 是一种低偏差高方差的集成学习策略,LightGBM-GRU 在偏差和方差上面都表现出了比LightGBM 更好的性能。R2表示预测变量与响应变量之间的线性关系,在测试集上LightGBM-GRU 的R2=0.84,证明股票波动率预测实验具有很高的实用价值。
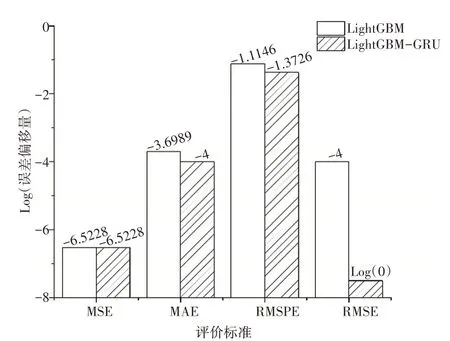
图11 模型在训练集和测试集上预测的偏量

表5 模型预测误差偏置表
仿真实验中所有的输入、输出是独立不相关的,这为高度相关的时间序列建模增加了困难,因为时间序列预测问题中,时间关联是很重要的因素[26]。GRU 是一个强大的时间数据处理模型,它用记忆细胞代替了传统神经网络中的隐层神经元,形成了信息循环结构[27]。因此,GRU 可以有效地将历史信息与当前输入数据关联起来,从而能够高精度地捕捉数据的动态特征。正如预期的那样,在126 只不同行业的股票波动率预测中,本文所提出的LightGBM-GRU 模型在所有模型中具有最好的预测效果,它在处理非正态分布的样本时能够更好地拟合离散点,反映了混合模型的稳健性。
实验分析与理论证明都表明了纠正学习策略的提升效果,为了进一步体现纠正学习策略的相对普适性,实验中将统计学中常用于时间序列预测的经典模型MLR(Multiple Linear Regression)作为基础模型,通过纠正学习策略设计出MLR-GRU 混合模型,同样将其应用到来自不同行业的126只股票3年的交易数据集中进行预测实验。
表6 和图12 为不同模型仿真结果的对比。结合MLR和MLR-GRU 的实验数据可以明显发现,纠正学习策略不论对经典的统计学算法还是经典的机器学习算法都有很好的提升效果,该策略对传统算法的提升具有相对的普适性。另外,对比发现LightGBMGRU 的性能要好于MLR-GRU,这表明基础学习器的性能会对纠正学习的混合模型性能产生较大影响。因此纠正学习算法作为一种元模型,在实际的工程实践中,可以根据面临的数据问题,自由选择恰当的模型作为纠正器和基础学习器。
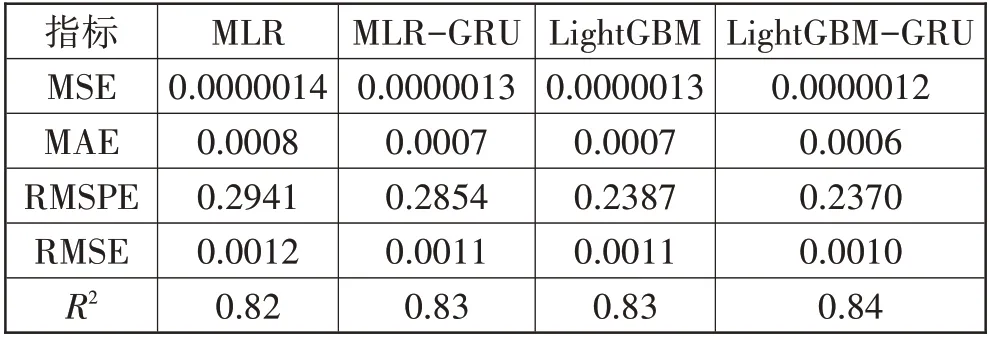
表6 2种纠正学习模型误差对比表
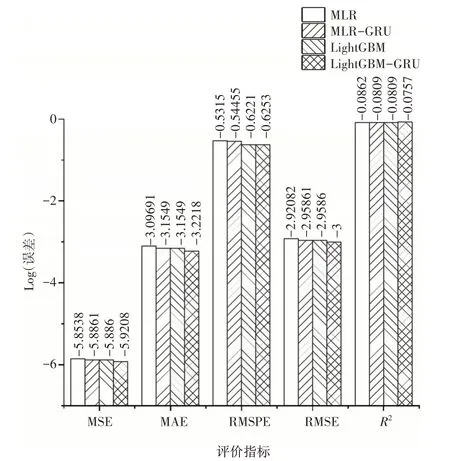
图12 2种纠正学习模型误差对比图
3 结束语
本文对3年内126只不同行业的股票波动率预测问题进行仿真实验,得出以下结论:
1)根据纠正策略设计出来的LightGBM-GRU 模型预测结果比LightGBM 有更低的误差率和更高的泛化能力,该模型可以帮助解决股票市场非线性仿真的难题。
2)神经网络作为纠正器参与工程应用,可以使深度学习框架达到降维的效果。
3)通过仿真证实了纠正学习策略是一种很有前景的算法,并且通过分析给出了该策略的理论证明。未来它可广泛应用于其他预测领域,可以为解决智能算法通用性有限与工程问题多样性之间的矛盾提供新的思路。
