含能材料自催化分解特性的快速鉴别方法
2023-03-21平川甘强张蕊都振华冯长根
平川, 甘强, 张蕊, 都振华, 冯长根
(1.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081; 2.西安航天化学动力有限公司, 陕西 西安 710025;3.陕西应用物理化学研究所 应用物理化学重点实验室, 陕西 西安 710061)
0 引言
自催化反应是指分解产物在反应过程中充当催化剂的一种反应类型[1],这类反应在含能材料的热分解过程中很常见[2-5]。自催化分解反应通常伴随着热量的突然释放,因此这类反应往往非常危险且难以预测。含能材料的自催化分解现象在发生剧烈反应(燃烧或热爆炸)之前,很长一段时间都不会有明显的温升现象,一旦产生明显的温升就会迅速成长为燃烧或热爆炸[6],因此如何快速准确地鉴别自催化反应并判断自催化反应强度,一直是研究的热点和难点[7-9]。
在以往的研究中,往往将具有自催化特性的物质按照n级反应进行动力学计算分析[10-12],但会造成危险性评估的偏差。为准确描述物质的自催化反应,1944年Prout等[13]提出Prout-Tompkins反应模型,描述了高锰酸钾的自催化热分解过程。1994年Dien等[14]基于Prout-Tompkins模型提出了通用性更强的Benito-Perez反应模型,并给出了判断自催化反应强弱的依据。后续的Kamal-Sourour反应模型[15]、Avrami-Erofeev反应模型[16-19]等都是基于以上两种反应模型的改进,以上自催化反应模型的提出对于研究自催化反应的进程提供了有利条件。
表1给出了常见自催化反应动力学模型的机理函数表达式。需要特别指出的是,机理函数是定量描述反应速率随反应进度α变化关系的函数,并无分布函数特性。
1987年Keenan[20]提出了利用差示扫描量热仪(DSC)或微热量热仪(C80)鉴别自催化反应的等温测量方法,通过测量反应放热速率曲线可靠鉴别自催化反应。2002年Leila等[21]利用1阶动力学反应模型拟合计算出物质在初始分解阶段的反应活化能,认为高于220 kJ/mol的物质反应类型均为自催化反应。Malek[22]、Gotor等[23]、Sbirrazzuoli等[24]均提出了基于DSC的自催化反应鉴定方法,但此种方法的起始计量温度难以确定,起始温度过高或过低均会对试验结果产生较大误差,影响自催化反应的判定。2013年Roduit等[25]研究了初始转换率对自催化反应进程的影响。2014年Yang等[26]基于Roduit的研究提出了“中断回扫法”鉴别自催化反应。2016年Wang等[27]利用中断回扫法完成了部分含能材料自催化反应的准确鉴别,但该方法需要进行多次测量,测试过程较为繁琐。

表1 常见的固体自催化反应机理函数Table 1 Common autocatalytic reaction mechanism functions for solid
21世纪以来,绝热加速量热仪(ARC)等被大量应用于含能材料的热分解动力学研究中[28-30]。与DSC相比,ARC可以进行更大样品量的试验,更接近物质反应的真实环境。2018年Dong等[31]利用ARC对危险物质的自催化反应强度等级进行了分类,该方法需要准确计算热动力学参数。2020年Zhao等[32]提出了无需计算动力学参数的绝热环境自催化反应鉴别方法,拓展了绝热设备在自催化反应研究方面的应用,但该方法需要对物质进行完整的放热试验,对于含能材料的试验极有可能造成严重的爆炸事故和精密仪器的损坏。
本文基于绝热量热法,提出一种在自催化反应初期即可完成自催化反应鉴别的方法,并可根据特征信号判断自催化反应强度。该方法能够避免含能材料测量过程中的热爆炸现象发生,同时快速准确地鉴别出含能材料热分解反应类型,并判断自催化特性强度。
1 鉴别方法的原理分析
1.1 理论依据
表1所示机理函数f(α)体现了反应速率与反应物(部分包括产物)物质的量的相关性。由于遵循不同的反应机理,在反应物转化率发生变化时,绝热反应体系的反应速率必然会有不同变化。为量化这种变化,选取5种常见的机理函数(1级反应,2级反应,P-T反应,A-E反应,Cnm反应),为模拟真实的分解反应,以α1=0.06为初始计算点,计算机理函数随转化率变化的比值f(αn)/f(α1),结果如图1所示。

图1 不同机理函数f(αn)/f(α1)随转化率α变化的计算结果Fig.1 Calculation of different mechanism functions f(αn)/f(α1) with the conversion rate α
由图1可见,与n级反应相比,自催化反应(P-T反应、A-E反应、Cnm反应)的f(αn)/f(α1)值会随着转化率的增大迅速升高,且存在最大值,到达最大值后比值进入下降区间,转换率接近1时f(αn)/f(α1)值无限逼近于0。在上升区间内自催化反应的f(αn)/f(α1)初始值始终大于1。而n级反应的f(αn)/f(α1)始终在1以下。利用这种差异可以鉴别热分解反应的反应类型。
针对不同的反应机理,都有特定的机理函数f(α)所决定的特性形状,这会体现到反应体系的反应速率中。反应体系的反应速率一般可表示为
(1)
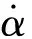
由图1可以看出,f(αn)/f(α1)比值越高,该机理函数的数值增长速度越快,反应自催化特性也就越强,反应越不容易得到控制,因此f(αn)/f(α1)能够较好地量化自催化反应机理函数f(α)的“加速特性”(自催化特性)。此结论对具有自催化特性物质的鉴别和自催化反应强度分类具有重要意义。
1.2 鉴别方法的公式推导
理想绝热条件下,反应物分解放出的热量全部用于自身温度的提升,由热力学第一定律可知,在绝热放热反应体系下存在:
dQ=Q∞×dα=cp×m×φ×dT
(2)
式中:dQ为任一时间段内反应体系的放热量;Q∞为反应总放热量;dα为任一时刻反应物的转化率;cp为反应物的比热容,理想绝热条件下反应体系压强不变,因此选用cp为反应物的定压比热容;m为反应物的比热容和反应物质量;φ为绝热反应体系的热惯性系数,理想状态下其值为1;dT为任一时刻反应体系的绝热温升。
假设cp不随温度的变化而变化,令c=cpmφ/Q∞,对于任一确定的反应物,c为常数,有
(3)
式中:dt为转化率由α1变化至αn所用的时间。根据阿伦尼乌斯定律,有
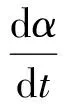
(4)
对于同一种反应物,在不同的转化率变化区间内,有
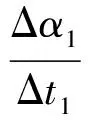
(5)
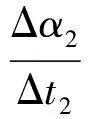
(6)
式中:T1、T2分别为不同转化率对应的温度。
令Δt1=Δt2,式(5)与式(6)相除,可得
(7)
结合式(3)可得
(8)
式(8)的意义在于,在已知反应物绝热放热反应过程中的活化能Ea和任意两时刻反应体系温度及两时刻对应的温度变化速率后,即可获得机理函数随转化率变化的比值f(αn)/f(α1)。根据比值f(αn)/f(α1)即可完成自催化反应以及反应强度的判断。通过ARC进行的绝热量热试验往往很难获得物质精确的Ea,但在f(αn)/f(α1)的计算过程中,Ea往往对反应结果的判断没有较大影响,此结论在本文第3节会有详细阐述。为更好地验证公式推导的正确性,本文采用数值模拟方法对鉴别方法进行验证。
2 绝热体系分解反应模型建立与计算分析
2.1 绝热体系分解反应模型的建立
参考Zhao等[32]的研究成果,建立对于绝热反应体系的放热量关系式如下:
(9)
式中:Tf为反应终止温度;Ton为反应初始放热温度;Q0为反应初始放热量;α0为初始转化率。
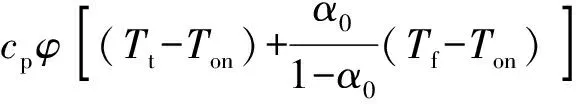
(10)
(11)
式中:Qt、Tt和αt分别为t时刻反应放热量、反应温度和转化率。由式(11)可得
(12)
根据阿伦尼乌斯定律,有
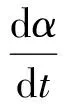
(13)
(14)
由此可得4种常见反应类型的dT/dt的表达式,如表2所示。
由表2可知,根据式(11)、式(12)以及反应机理函数f(α),在已知反应体系总放热量Q∞和反应初始放热温度Ton的情况下,即可完成不同反应机理下绝热量热试验过程的模拟计算。
2.2 数值计算分析
首先计算φ=1时1级反应、2级反应、P-T反应、Cnm反应和A-E反应的dT/dt与T之间的关系,如图2所示。数值计算中用到的参数如表3所示。由图2和表3可以看出,P-T、A-E反应和Cnm反应的放热速率普遍高于1级反应和2级反应。

表2 4种常见反应类型的dT/dt的表达式Table 2 Expressions for dT/dt for several common reaction types
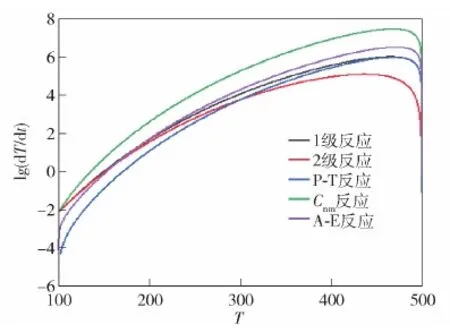
图2 φ=1时dT/dt随T变化Fig.2 dT/dt varies with T for φ=1
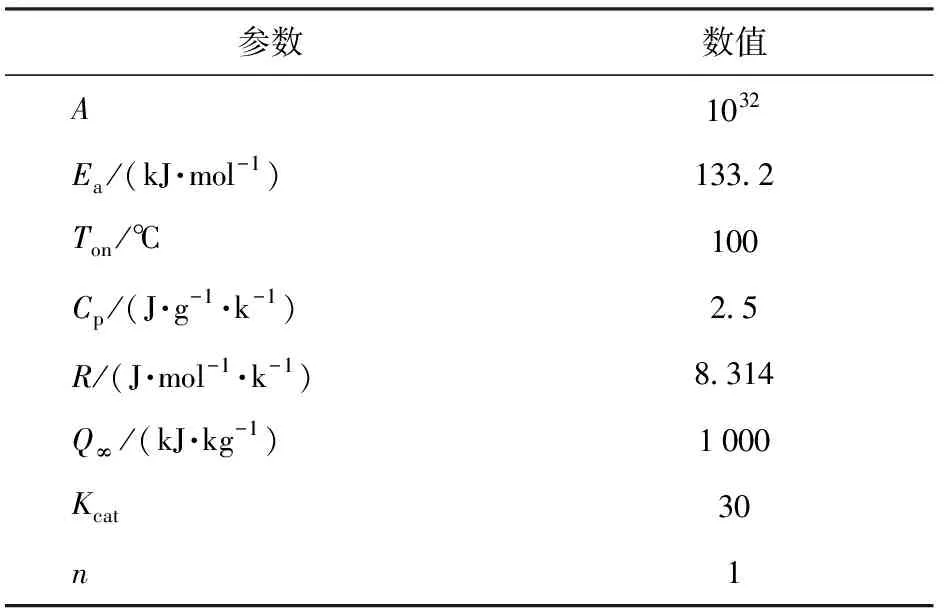
表3 仿真计算参数Table 3 Parameters used in the simulations

图3 不同热惯性下5种反应机理的dT/dt随α变化Fig.3 Variation of dT/dt with α for five reaction mechanisms with different thermal inertia
计算φ取值分别为1、2、3、4、5、6时1级反应、2级反应、P-T反应、Cnm反应和A-E反应的dT/dt与转化率α之间的关系,如图3所示。由于绝热量热仪的实际初始采样值为0.02 ℃/min,将模拟计算时的dT/dt起始计算点α0也设置在0.02 ℃/min所对应的转化率。
由图3可见,当热惯性系数过大时(如φ=6),2级反应出现了检测不到放热信号(反应体系的放热速率始终小于0.02 ℃/min)的情况。表2中dT/dt与热惯性系数呈反比。由式(2)可见,反应体系的绝热温升与热惯性系数有直接关系,热惯性系数越大,反应的绝热温升越小。式(11)表明了反应体系的绝热温升直接影响反应体系的实时转化率,对于热惯性系数大的反应体系,每升高1 ℃对应反应体系的转化率增量也就越大,从而解释了热惯性过大时检测不到放热信号的现象。因此热惯性过大时(如图3中φ取值为5、6),可检测到放热信号时反应体系转化率达到了一个较高的值,进入了图1所示转化率α下降区间内,造成了dT/dt随转化率的增加而降低。
图4所示为热惯性对4种反应机理函数初始转化率的影响规律。由图4可见,热惯性越大,起始考察点对应的起始转化率也越大,这是因为热惯性越大,样品容器升温所需热量占总放热量比例也就越大,导致反应体系的升温速率下降,绝热温升降低,进而会出现起始考察点的放热信号出现“滞后”的现象。对比可见,Cnm自催化反应受热惯性影响较小,A-E反应和P-T反应次之,2级反应受热惯性影响最大。

图4 热惯性对4种反应机理函数初始转化率的影响Fig.4 Effect of thermal inertia on the initial conversion rate of the four reaction mechanism functions
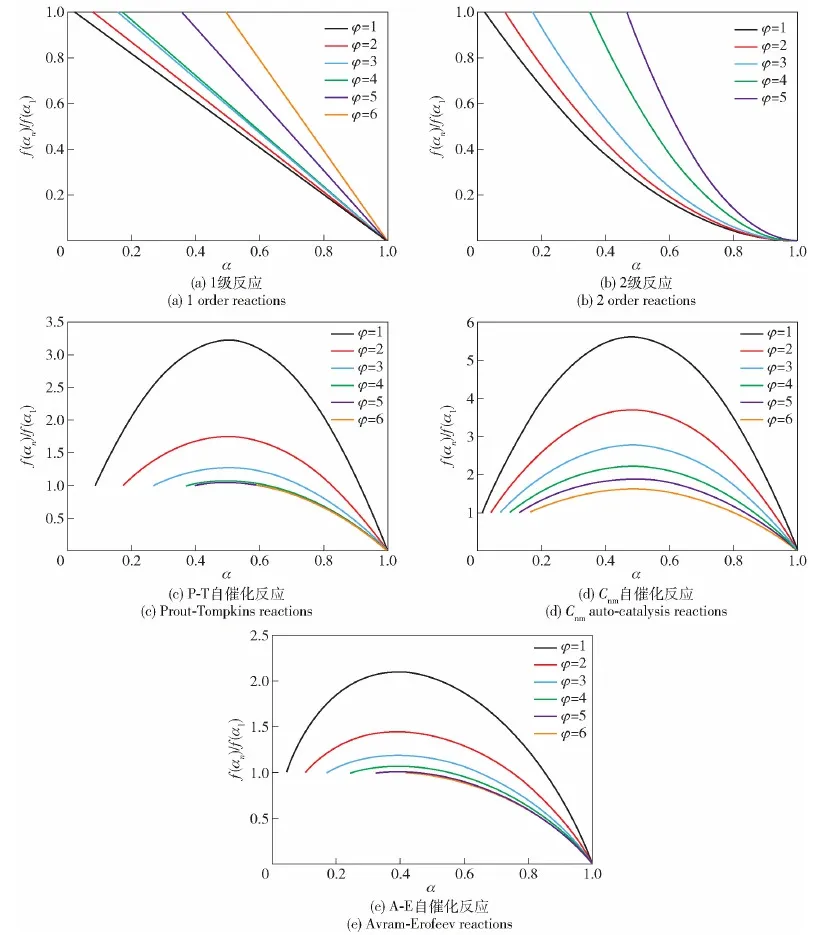
图5 不同热惯性下5种反应机理函数随α变化Fig.5 Variation of the five reaction mechanism functions with α for different thermal inertia
图5为根据仿真结果计算出的不同反应机理函数和热惯性系数下的f(αn)/f(α1)值。由图5可见,无论是n级反应还是自催化反应,在转化率接近1时f(αn)/f(α1)值均无限接近于0;但n级反应的f(αn)/f(α1)值从初始值1开始单调递减,自催化反应的f(αn)/f(α1)值从初始值1开始逐渐上升,到达一个峰值后再逐渐下降至0。
表4给出了数值模拟中5种反应机理函数不同热惯性系数下的f(αn)/f(α1)最大值。由表4可见,无论哪种热惯性系数条件下,f(αn)/f(α1)值的大小排序均为Cnm>P-T>A-E,表明3种自催化反应机理函数的自催化特性强度排序为Cnm>P-T>A-E。
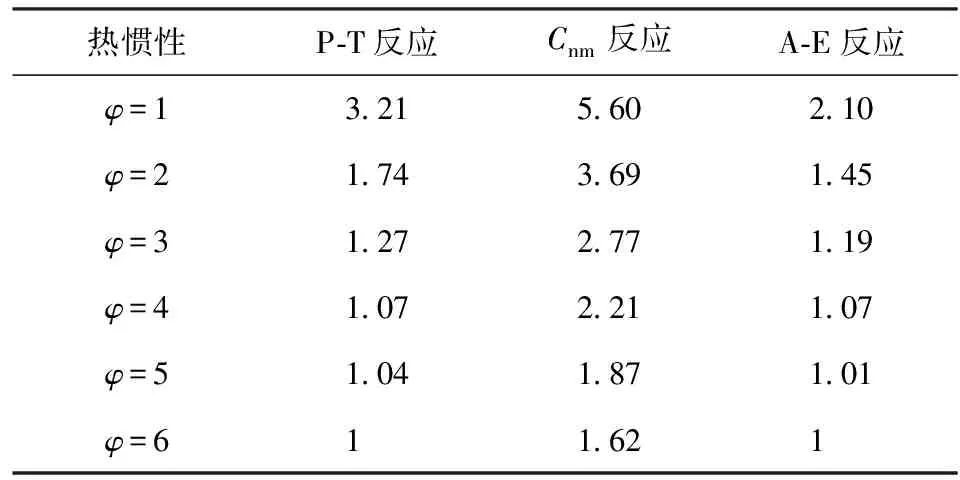
表4 模拟计算自催化机理函数的 f(αn)/f(α1)最大值Table 4 Calculated maximum value of f(αn)/f(α1) by the autocatalytic mechanism function
在部分较大的热惯性系数计算条件下,自催化反应机理函数的f(αn)/f(α1)初始值在1以下,这是因为热惯性系数过大导致出现初始放热信号时反应体系的转化率在机理函数数值的下降区间内。因此,在实际测量过程中应适当增加样品量以减小热惯性,避免起始特征信号出现在图5中机理函数数值的下降区间内。
3 含能材料的绝热量热试验与结果分析
3.1 试验样品
DTBP与甲苯的混合物在放热过程中严格遵循1级反应模型[31],因此选取20%DTBP与甲苯的混合溶液、超细HNS-Ⅳ、BNCP、CL-20、CMC-LA 5种样品进行绝热量热试验。本文试验所用20%DTBP与甲苯混合溶液为分析纯99.99%,超细HNS-Ⅳ粉体粒度分布为0.2~20 μm,与普通粒径HNS-Ⅳ相比,超细HNS-Ⅳ放热反应更为剧烈,反应特征信号更易辨别[33]。以上材料均为实验室自制,纯度超过99%。
3.2 试验条件
利用德国耐驰仪器公司ARC254型绝热加速量热仪对样品进行初始放热阶段的测量。为精确测量样品的放热信号,选用H-W-S模式,灵敏度为0.02 ℃/min,升温速率2 ℃/min,升温台阶5 ℃。测试样品容器选用耐驰NIB010816型Ti质样品球。为防止样品发生剧烈的放热反应,放热温度紧急停止阈值设置为1.0 ℃/min。
3.3 绝热量热试验结果
考察以上5种材料从0.02 ℃/min~0.50 ℃/min的放热过程温度变化情况。为便于数据统一,将5种材料的起始放热速率考察点设置为0.02 ℃/min,获得20%DTBP与甲苯混合溶液、HNS-Ⅳ、BNCP、CL-20、CMC-LA热分解初始阶段放热曲线如图6所示。由图6可见,初始分解温度随热惯性系数的增加而升高,与图5中的仿真计算结果一致。在放热过程中,反应温度随时间的增长随时间的增长呈指数上升,表明0.02 ℃/min~0.50 ℃/min放热过程中产物的热分解均为增速反应。
3.4 试验结果分析
根据图6结果计算5种测试样品的f(αn)/f(α1)值,结果如图7所示,由于没有准确计算各样品的活化能Ea,暂时将计算所需Ea统一设置为180 kJ/mol。为便于数据统一,将5种材料的初始采样放热速率设置在了0.02 ℃/min。
由图7可以看出,随着反应温度的升高,20%DTBP与甲苯混合溶液绝热放热反应的f(αn)/f(α1)值自1开始逐渐下降,表明20%DTBP与甲苯混合溶液的放热反应为n级反应,与Dong等[31]分析结果一致。HNS-Ⅳ、BNCP、CL-20、CMC-LA的f(αn)/f(α1)计算值均在1以上,且该计算值随着时间的增加而增加,表明以上4种含能材料的绝热热分解过程均为自催化反应,与Lee等[34]、周建华等[35]、王凯等[36]和刘剑超等[37]的研究结果一致。根据各个样品计算结果可见,热惯性越大,f(αn)/f(α1)的值越小,即自催化反应的特征信号随热惯性系数的增大而降低,较大的热惯性能够降低自催化反应的反应强度。

图6 5种样品的热分解初始阶段放热曲线Fig.6 Exothermic curves for the initial stages of thermal decomposition of the five samples
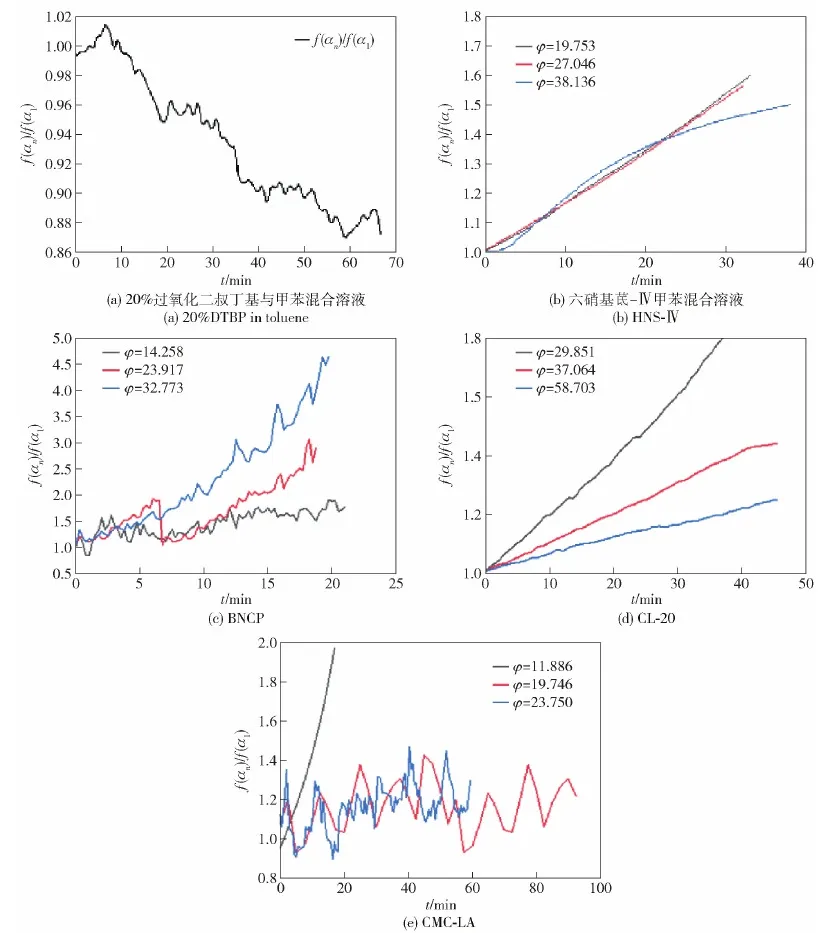
图7 5种样品的f(αn)/f(α1)计算值Fig.7 Calculated values of f(αn)/f(α1) for the five samples
为考察活化能Ea对f(αn)/f(α1)值的影响,将Ea分别取100 kJ/mol、150 kJ/mol、200 kJ/mol和250 kJ/mol,计算不同Ea时f(αn)/f(α1)值。表5 给出了f(αn)/f(α1)值的计算条件,其中不同活化能数值用/分隔开。根据表5中的条件计算得出的f(αn)/f(α1)值见图8。
由图8可见,f(αn)/f(α1)计算值与活化能Ea值呈反比,Ea值越大,f(αn)/f(α1)计算值越小。但无论是n级反应还是自催化反应,Ea值均不影响f(αn)/f(α1)计算值随时间变化的总体趋势,即Ea取不同值时,n级反应的f(αn)/f(α1)计算值仍为随时间单调递减,且计算值全部在1以内,自催化反应的f(αn)/f(α1)计算值仍为随时间单调递增,且计算值全部在1以上。这是因为活化能Ea值代表了反应发生的难易程度,Ea值越大,反应越难发生,反应速率趋于平缓,表现在图8中即为f(αn)/f(α1)值较小。机理函数f(α)代表了反应进行方式与反应物消耗的相关性,Ea值虽能影响反应速率却不能影响反应进行方式的本质,因此活化能Ea的取值不影响f(αn)/f(α1)计算值随时间的整体变化趋势,也不影响基于f(αn)/f(α1)计算值的反应类型判断。
4 结论
本文基于绝热量热法提出了可快速判断物质自催化分解特性和强度的方法,基于n级反应和自催化反应模型研究了热惯性对机理函数随时间变化率的比值f(αn)/f(α1)的影响规律,利用绝热量热法测量5种样品并进行自催化特性分析。得到如下主要结论:
1)仿真结果表明,3种自催化反应机理函数的自催化特性强度排序为Cnm反应>P-T反应>A-E反应,热惯性系数深刻影响着物质的绝热放热过程。热惯性系数越大,物质的放热反应强度越小,与此同时自催化反应的特征信号越弱。
2)f(αn)/f(α1)计算值越高,表明该物质分解自催化特性越强。计算表明,20%DTBP与甲苯混合溶液的绝热热分解反应为n级反应,HNS-Ⅳ、BNCP、CL-20和CMC-LA的绝热放热反应为自催化反应。
3)活化能Ea的值不影响f(αn)/f(α1)计算值随反应时间的走势,也不影响基于f(αn)/f(α1)计算值判断出的反应类型结果。因此本文方法可迅速完成反应类型的鉴别和自催化特性强度的判断,相对于等温法、中断回扫法等方法可大大减少试验时间,并降低发生意外事故的危险性,可靠性有待进一步试验验证。

表5 f(αn)/f(α1)值的计算条件Table 5 Conditions for calculating the value of f(αn)/f(α1)
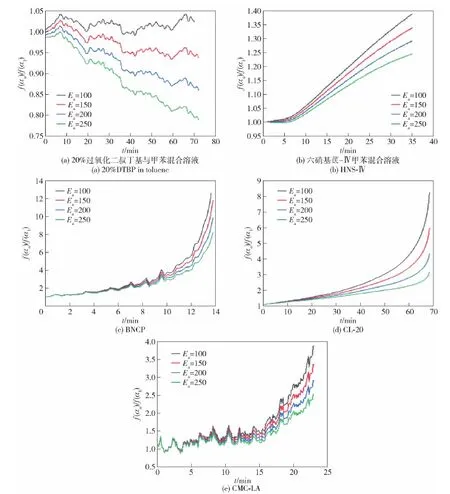
图8 不同活化能下5种样品f(αn)/f(α1)计算值Fig.8 Calculated values of f(αn)/f(α1) for the five samples at different activation energies
