水下爆炸冲击波和气泡载荷对典型圆柱壳结构的毁伤特性

2023-03-21张轶凡刘亮涛王金相李恒唐奎

兵工学报 2023年2期

张轶凡，刘亮涛，王金相，李恒，唐奎

(1.南京理工大学瞬态物理国家重点实验室，江苏南京 210094； 2.海军研究院，北京 100161)

0 引言

随着国际形势的日益严峻和地区冲突的不断升级，海上作战成为一种重要形式，鱼雷是目前海军水下作战的重要武器装备，同时水下爆炸也成为水中作战的主要毁伤方式之一。水中结构物在遭受水下爆炸作用时，冲击波及气泡载荷是对结构产生毁伤效果的主要因素。对于舰船等水下结构物，鱼雷在其近场爆炸造成的危害十分巨大，爆炸载荷会对结构物的整体强度造成巨大破坏。目前针对水下爆炸对舰船单位的毁伤研究，国内外学者已经做了大量的工作[1-5]，得出了很多具有指导性的结论。但与此同时，鱼雷这一海军武器本身也作为一种水下结构物存在，在航行过程中同样会受到反鱼雷武器的影响和破坏。因此，研究水下爆炸冲击波和气泡载荷对鱼雷典型圆柱壳结构的毁伤特性，具有重要的军事意义。

姚熊亮等[6]对冲击波与圆柱壳结构相互作用过程中产生的压力场进行仿真和分析，给出了在不同板厚与爆距下圆柱壳周围的压力场分布情况。刘东等[7]基于内嵌的水下爆炸载荷计算方法和声固耦合方法，对不同壳体厚度及肋骨间距下的环肋圆柱壳在非接触爆炸中的变形响应进行了研究。仝志永等[8]采用声固耦合算法分析了填沙薄壁圆柱壳结构水下爆炸作用下的弹塑性形变和损伤的破坏形式。Wu等[9]针对破片和爆炸载荷联合作用下金属圆柱壳结构的动态响应以及破坏效应进行了实验和数值模拟分析。沈晓乐等[10]采用应变测量的方法对加肋圆柱壳模型进行了模态分析。周游等[11]利用流- 固耦合法分析了不同装药设置条件下圆柱壳的爆炸变形模式特征，分析了爆源条件对圆柱壳动力响应及变形模式的影响规律。刘云龙等[12]基于不可压缩势流理论，运用边界元方法研究了攻角对圆柱壳附近水下爆炸气泡动态特性的影响，并将双渐进法与有限元法相耦合，研究了圆柱壳结构受水下爆炸载荷作用的冲击损伤问题和主要损伤模式[13]。纪冲等[14]对充液及内空圆柱壳在爆炸载荷下动力屈曲响应特性及不同工况下圆柱壳的变形破坏模式进行了研究。汪浩等[15]研究了近距离非接触爆炸作用下的气泡脉动载荷以及气泡溃破高速射流载荷对内加筋圆柱壳结构的毁伤机理，以及结构参数、药包位置对结果的影响。综上所述，目前已有的研究工作对爆炸距离及方位相关参数影响规律的研究较少，仍有大量工作需要完成。

为研究鱼雷中部位置在爆炸作用下的响应情况，本文将鱼雷头部和尾部的典型特征去除，简化为圆柱壳结构进行分析。采用LS-Dyna软件对其在近场爆炸冲击作用下的毁伤特性进行研究，详细探讨爆距、药包方位等相关物理量对圆柱壳结构变形特征与毁伤特性的影响。

1 水下爆炸毁伤算法设置及材料模型

缩比后的鱼雷典型圆柱壳结构长度为1.1 m，半径0.081 m，壳体厚度0.003 m；在圆柱壳上均匀分布有3条加强肋，加强肋间距为0.5 m，宽度为0.03 m，厚度0.006 m。

1.1 水下爆炸圆柱壳结构模型算法设置

在LS-DYNA软件中建立圆柱壳结构水下爆炸计算模型，采用任意拉格朗日- 欧拉(ALE)算法处理圆柱壳结构与水介质、空气之间的相互作用，其中空气和水介质采用欧拉算法，圆柱壳结构采用拉格朗日算法。为保证计算的稳定性，对圆柱壳结构进行网格划分时尽可能满足对网格形状的优化；同时为保证流固耦合的准确性，对水域中部区域的网格进行加密，以保证此区域内的欧拉单元尺寸与圆柱壳中部的拉格朗日单元尺寸基本一致，加密区域网格大小为0.01 m×0.01 m。各部分网格划分如图1所示。

图1 各部分网格划分Fig.1 Meshing of various parts

计算模型示意图如图2所示，数值计算采用国际单位制。其中欧拉域大小为4 m×4 m×6 m，空气层厚度为0.3 m，对空气域上表面设置无反射边界条件，将空气域、水域的侧表面以及水域的底面设置为固壁边界条件，TNT炸药被放置在计算域中心位置，爆炸深度为2.7 m。

图2 数值模拟计算模型示意图Fig.2 Schematic diagram of numerical simulation model

最终得到各部分网格数量如表1所示。

表1 各部分网格数量Table 1 The number of grids in each part

1.2 材料模型

圆柱壳的本构模型选用Johnson-Cook模型，失效模型选用Johnson-Cook失效模型。Johnson-Cook模型是一种基于实验得到的、能够反映应变率强化效应和温升软化效应的材料模型[16]，其应力表达式为

(1)

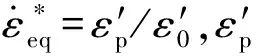
采用单元最大失效应变控制单元强度，等效塑性应变累计损伤度控制材料的破坏断裂，当单元的有效累计塑性应变达到失效应变时，发生失效侵蚀，单元损伤系数表达式为

(2)

式中：D为损伤系数，在0～1之间变化，初始状态下D=0，当D=1时材料失效；Δεp为单个时间步的塑性应变增量；εf为当前时间步对应的破坏应变，是当前应力、应变、应变率及温度的函数，

(3)

D1～D5为材料参数；σ*=p/σeff为应力状态参数，p为正压力，σeff为等效应力；T*为温度状态参数。

模型中圆柱壳采用铝合金材料[17-18]，如表2所示。水介质和空气的材料本构模型采用常见的空物质模型，水介质采用Gruneisen状态方程[19]，其表达式为

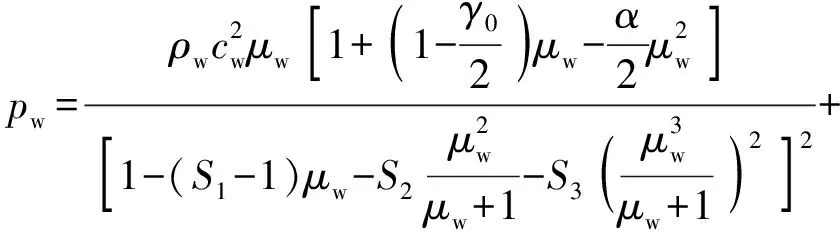
(γ0+αμw)Ew

(4)

式中：pw为介质中的压力；ρw为材料密度；cw为材料声速；μw=1/Vw-1，Vw为相对体积；γ0为材料Gruneisen系数；α为γ0的修正系数；S1、S2、S3为Gruneisen状态方程材料常数；Ew为单位体积初始内能。水的材料参数[20]如表3所示。

空气采用Liner Polynomial多项式状态方程[19]，由式(5)定义：

(5)

式中：pa为介质中的压力；μa=1/Va-1，Va为相对体积；Ea为单位体积初始内能；Ci(i=0～6)为状态方程参数。空气材料参数[20]如表4所示。

表2 铝合金材料参数Table 2 Material parameters of aluminum alloy

表3 水的材料参数Table 3 Material parameters of water

表4 空气材料参数Table 4 Material parameters of air

爆轰产物的压力采用JWL状态方程[19]来描述，其一般形式为

(6)

式中：pt为爆轰产物的压力；V为爆轰产物和炸药的相对体积，为无量纲量；Et为单位体积内能；At、Bt、R1、R2、ω为待拟合参数。TNT炸药的JWL参数[20]如表5所示。

表5 TNT材料参数Table 5 Material parameters of TNT

2 算法有效性验证

通过与文献[21]中的实验进行对比，对ALE数值模拟方法进行验证。采用4 g的PETN炸药在2 m的正方体水箱中进行爆炸试验，炸药安置在厚度0.02 m水平钢板下方0.19 m处。在数值模拟中采用TNT炸药对实验中的PETN炸药进行等效替代，PETN和TNT的单位体积爆轰能量分别为9×109J/kg和7×109J/kg，通过计算得到等能量情况下4 g PETN炸药对应的TNT炸药质量为5.2 g。不同时刻下气泡形态的实验和仿真结果的对比如图3所示。爆炸初期，气泡在内外压差的作用下呈球形膨胀，膨胀到一定大小后，逐渐受到上部平板的影响，气泡上部形态逐渐变得平坦，这一现象随着气泡的继续膨胀变得更加明显，通过图3(d)可以直观地观察到这一现象；气泡膨胀到最大后在内外压差的作用下开始收缩，如图3(e)所示；由于气泡上部钢板的存在，收缩阶段气泡上部的收缩速度明显小于气泡下部，表现为水平钢板对气泡的吸引作用，使得气泡在收缩阶段呈现为近似圆锥的形态，如图3(h)所示；气泡在收缩的最后阶段形成了一个贯穿气泡中部的水射流，对水平钢板造成了射流抨击。通过与实验中气泡形态演变规律的对照，发现数值模拟方法得出的气泡形态结果与实验结果能够吻合；同时，实验中爆炸气泡的第1次脉动周期为45.062 ms，通过数值模拟得到的气泡周期为51.5 ms，在气泡周期这一结果上存在一定误差，究其原因可能是实验中的炸药未完全起爆。根据TNT炸药无限水域爆炸气泡周期经验公式[22]：

(7)

式中：Tb为爆炸气泡周期；W为装药量；Z为爆炸水深，可以计算出无限水域中5.2 g TNT炸药在0.8 m水深下的爆炸气泡周期为50.3 ms，而此数值模拟算法下同工况气泡周期为50.9 ms，数值模拟结果与理论计算值的误差为1.19%；由此表明此数值模拟方法的计算精度较高，能够满足研究的需求。

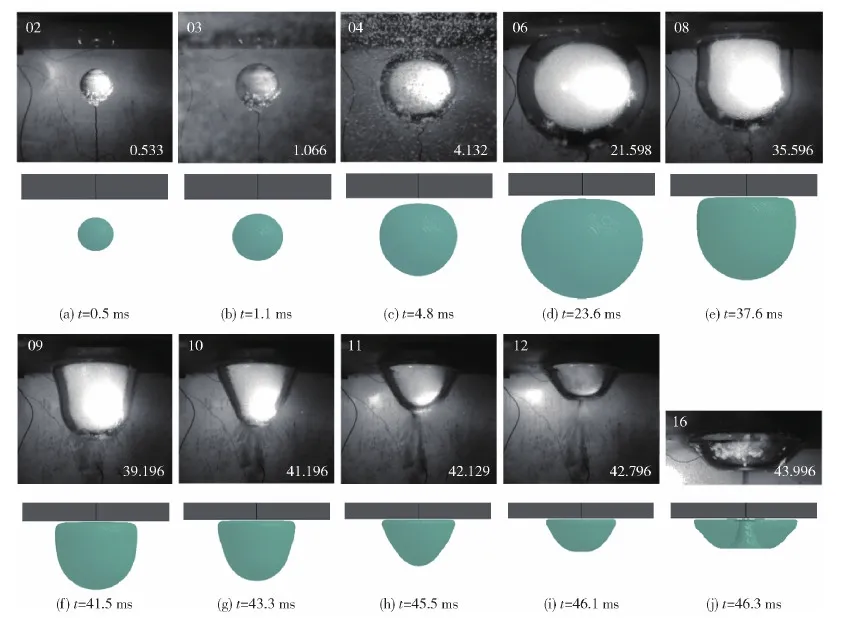
图3 不同时刻下气泡形态的实验与数值模拟结果对比Fig.3 Comparison of experimental and numerical results of bubble shape

3 计算结果分析

3.1 不同爆距下冲击波和气泡载荷对圆柱壳的毁伤特性分析

在保持TNT装药量、爆炸水深、边界条件不变的情况下，通过改变TNT药包与圆柱壳的相对距离，研究不同爆距下冲击波和气泡载荷对圆柱壳的毁伤特性。

3.1.1 工况设置

设置TNT药量为27.0 g，爆炸深度2.7 m，药包到圆柱壳的距离从0.05 m到0.30 m进行设置，得到6组不同工况，如表6所示。

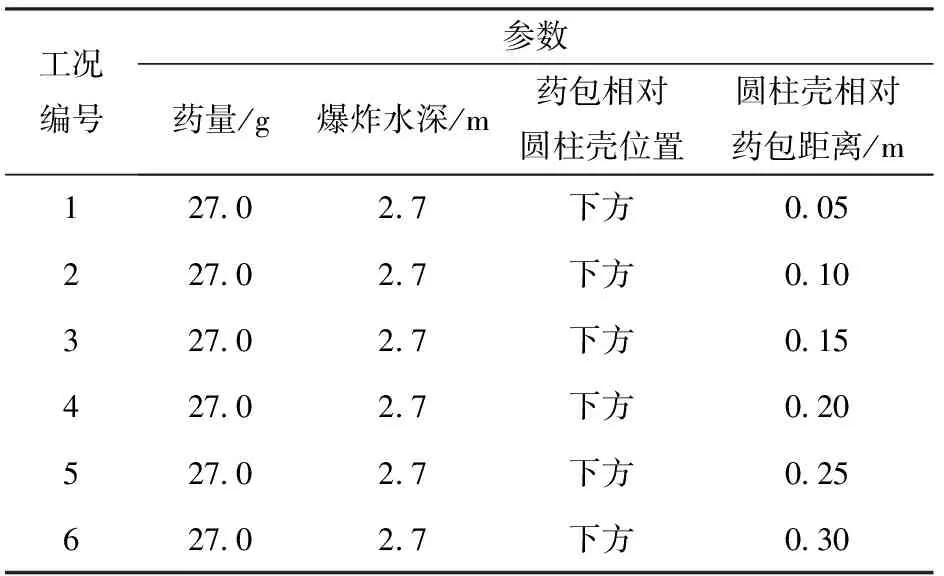
表6 计算工况Table 6 Simulation conditions

3.1.2 水下爆炸气泡与圆柱壳结构的响应过程分析

取工况1进行过程分析，当药包位于圆柱壳下方0.05 m的位置时，气泡形态随时间的变化情况及圆柱壳在爆炸气泡作用下的响应特性如图4所示。图4中呈现了爆炸气泡第1个气泡脉动周期内8个典型时刻下的流场速度情况以及圆柱壳的von Mises应力分布情况。

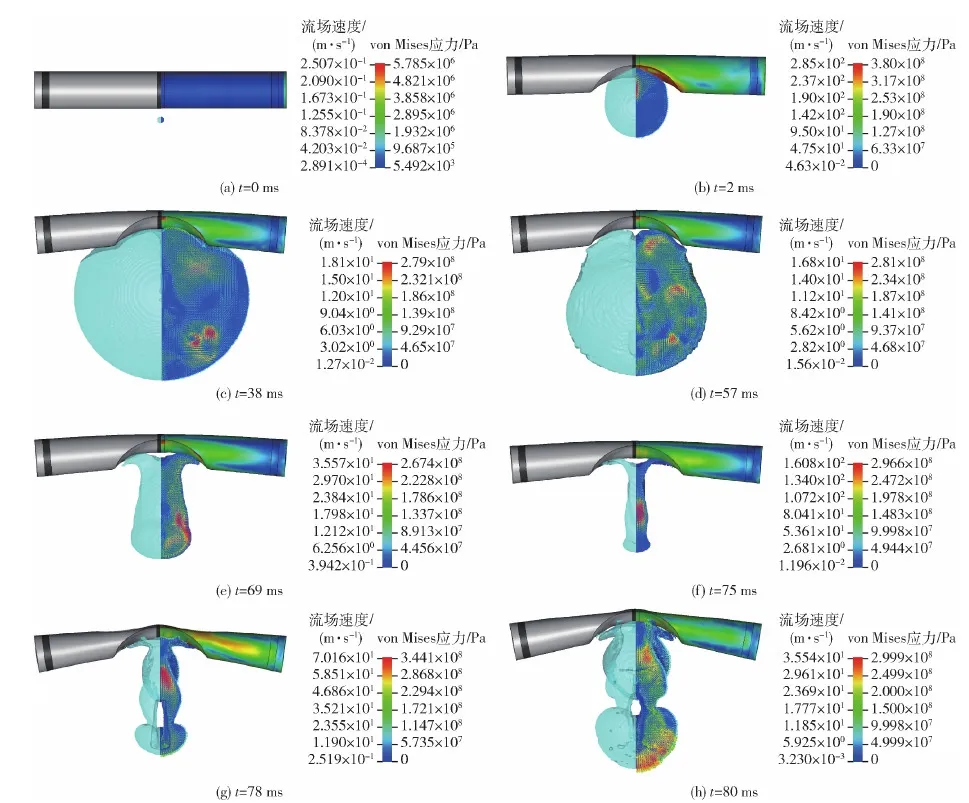
图4 爆距为0.05 m工况下的不同时刻爆炸气泡与圆柱壳相互作用效果Fig.4 Interaction between the explosion bubble and the cylindrical shell under the explosion distance of 0.05 m

取圆柱壳迎爆面上的单元以及药包与圆柱壳之间0.05 m处的参考点为研究对象，得到圆柱壳迎爆面压力、应力、塑性应变、挠度以及流场中的速度随时间变化曲线如图5所示。

对工况1中的水下爆炸过程进行分析。TNT药包以及圆柱壳的初始形态如图4(a)所示，炸药起爆前流场速度接近于0 m/s，圆柱壳上的应力主要来自静水压力；图4(b)时刻为起爆初期，气泡内部处于高压状态，气泡在内外压力差的作用下迅速膨胀，圆柱壳在爆炸冲击波的作用下产生了球面状凹陷变形，如图5中所示，冲击波阶段产生了极大的压力、应力应变、流场速度以及挠度，曲线均出现大幅上升；在图4(c)所示时刻，气泡膨胀到最大体积，此时气泡下部以及左右两侧能够呈现出较为标准的球形，圆柱壳在气泡作用下逐渐远离初始位置，并且在此刻圆柱壳整体的弯曲变形更明显；图4(d)展示了气泡膨胀到最大体积后收缩阶段的气泡形态，圆柱壳对气泡的吸引作用使得气泡上半部形态明显整体小于下半部分，同时圆柱壳随着气泡收缩也产生向下运动的趋势，这一时刻圆柱壳的变形情况未产生明显的变化，应力分布也与之前图4(c)基本一致，图4中各曲线在气泡膨胀后期和收缩前期的值均呈现小幅变化；图4(e)展示了气泡进一步收缩后所呈现出的现象，圆柱壳的影响使得气泡水平方向尺寸明显小于竖直方向，此时刻圆柱壳的形变没有发生明显变化；气泡收缩到最小体积后再次膨胀时的形态特征如图4(f)所示，此时气泡演化为长条状，气泡中部产生朝向圆柱壳的水射流，参考点的流场速度方向表现为竖直向上，从图5(b)中可以看到流场速度大小约为 40 m/s，同时脉动载荷和射流载荷对圆柱壳产生第2次冲击，图5中各曲线均出现第2次明显上升；在气泡第2次膨胀阶段，侧向射流的作用使气泡被分割成了上下两部分，如图4(g)和图4(h)所示，随着时间的推进，这一趋势更加明显，同时气泡脉动载荷及水射流载荷使得圆柱壳的凹陷程度进一步加深，在背爆面上形成了一个凸起，圆柱壳整体的弯曲变形也进一步扩大，图5(d)应变曲线和图5(e)挠度曲线出现了第2次阶跃。通过对此工况下的爆炸过程进行分析可以发现，冲击波载荷作用到圆柱壳后能使得圆柱壳在中部产生一个球面状的凹陷，同时圆柱壳整体也会产生一个小幅度的中拱弯曲，气泡脉动及射流载荷的作用进一步加大了圆柱壳中部凹陷的大小和整体的中拱弯曲程度，并且在背爆面形成了小幅度的拱起。

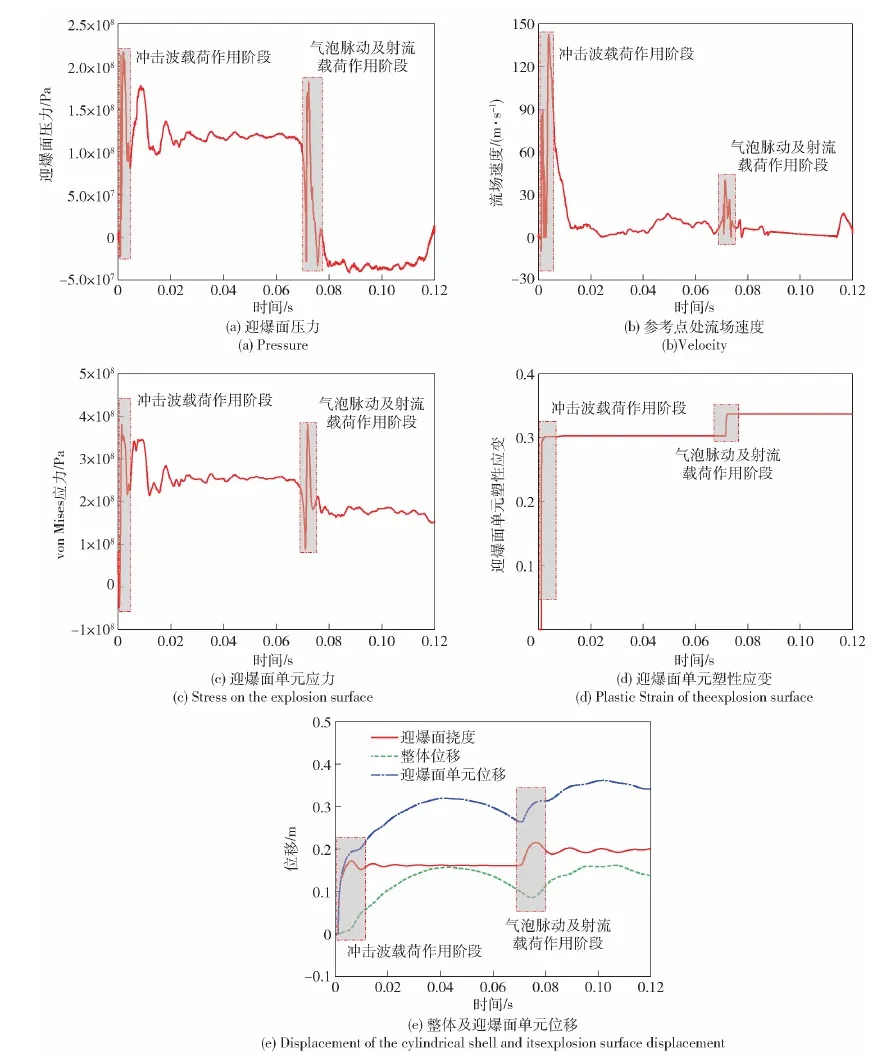
图5 圆柱壳迎爆面应力、应变及流场压力、速度变化情况Fig.5 Response of cylindrical shell and flow field

3.1.3 不同爆距下爆炸毁伤结果分析

图6为6个工况在同一时刻下圆柱壳的响应情况和爆炸气泡形态变化情况，通过云图分别展示了圆柱壳的塑性应变大小和流场的速度大小变化情况。图7为圆柱壳迎爆面上的单元挠度随时间变化情况。

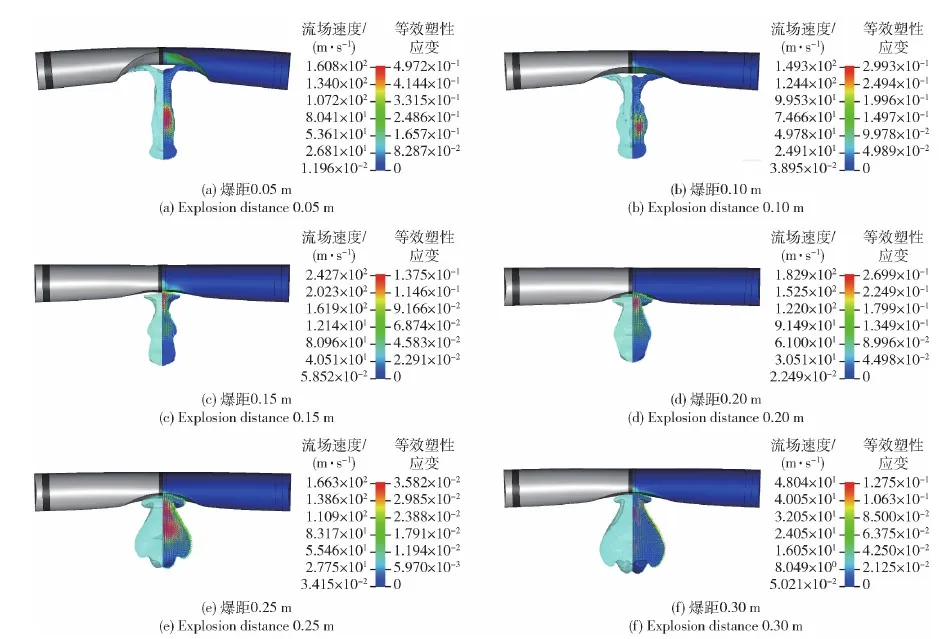
图6 不同爆距下爆炸气泡对圆柱壳的作用效果Fig.6 Interaction between the explosive bubbles and the cylindrical shell under different explosion distances

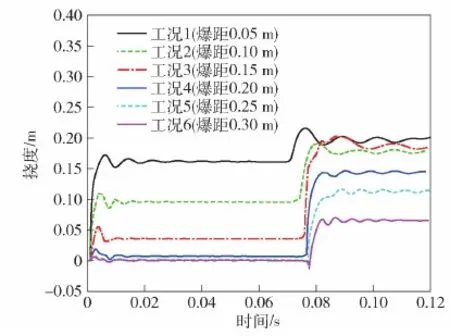
图7 不同爆距下迎爆面单元挠度变化情况Fig.7 Deflections of the cylindrical shell under different explosion distances

由图6和图7可知：随着爆距的增大，圆柱壳结构的变形呈减小趋势，当爆距为0.05 m时，圆柱壳表现为大变形，在冲击波作用下的挠度阶跃幅度很大，除形成大凹陷外，还产生了整体的弯曲变形，整体的弯曲现象在爆距增大到0.15 m时趋于消失；爆距的变化同时也影响了圆柱壳对气泡的作用效果，当爆距较小时，气泡在收缩阶段后期呈现为细长状，随着爆距的增大，同一时刻下的气泡形态逐渐呈短粗状。图8所示为仿真结果下气泡第1次脉动周期大小随爆距的变化趋势。由图8可见：爆距从0.05 m增加到0.3 m这一过程中，气泡周期从69 ms增长到了75 ms，表明气泡周期随着爆距的增大而增大，且增长率呈减小趋势；当爆距变化到足够大时，圆柱壳对气泡脉动的影响效果可以忽略不计，此时认为气泡脉动过程发生在自由水域中，且气泡脉动周期与自由水域中一致，根据第2节中TNT炸药无限水域爆炸气泡周期经验公式[22]计算可知，27 g的TNT炸药在自由水域中2.7 m深处爆炸时气泡的第1次脉动周期为76.1 ms，略大于爆距为0.3 m时的气泡脉动周期。由此可见，爆距对爆炸气泡第1次脉动周期有明显的影响作用，当爆距较小时圆柱壳对气泡的影响作用效果较大，使得气泡第1次脉动周期明显小于无限水域中的脉动周期，爆距较大时圆柱壳对气泡的作用效果较弱，气泡脉动周期更接近于无限水域中的值。

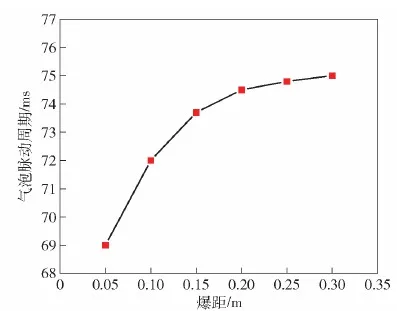
图8 气泡第1次脉动周期大小随爆距变化情况Fig.8 Variation of the first bubble pulsation period with explosion distance

取圆柱壳迎爆面上的单元以及TNT药包和圆柱壳之间距离药包0.1 m位置的观察点，对爆炸载荷下的迎爆面压力及流场速度峰值大小进行对比，得到两个参数随爆距变化曲线如图9所示。从图9中可以看出，冲击波在圆柱壳迎爆面产生的压力峰值随爆距的增大而减小，冲击波作用下流场速度峰值也有随爆距增大而减小的趋势，但曲线基本处于平缓。由于6组工况均为近场工况，气泡在收缩阶段均产生了朝向圆柱壳的水射流，形成射流载荷，这一载荷主要分布在气泡第2次膨胀初期，与气泡脉动载荷在时间维度上重合，不同爆距下的气泡脉动和射流载荷产生的压力大小及流场速度大小呈现出先增加后减小的趋势，且气泡脉动及射流在特定爆距下能够达到最大值。

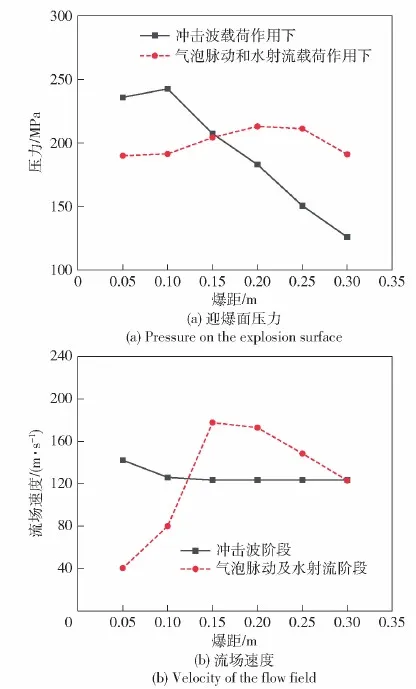
图9 迎爆面压力及距TNT药包0.1 m处观察点流场速度随时间变化情况Fig.9 Pressure on the explosion face and velocity of the flow field at the observation point with time

不同爆距下TNT炸药爆炸在冲击波阶段对圆柱壳结构产生的毁伤效果如图10所示。由图10可见：在爆距小于0.15 m时，冲击波能使得圆柱壳产生比较大的塑性变形，在圆柱壳中部形成局部凹陷，爆距达到0.2 m时，冲击波能使圆柱壳产生较小范围的塑性应变；爆距大于0.2 m时间，圆柱壳的塑性变形很小，可以忽略不计。

气泡脉动及水射流载荷对圆柱壳的毁伤作用如图11所示。由图11可见：在爆距为0.05 m和0.1 m的工况下，气泡及射流载荷使得圆柱壳产生了较明显的弯曲变形，在冲击波作用的基础上加大了塑性变形；与其他工况有所不同，爆距为0.15 m的工况下圆柱壳中部发生了单元失效现象，表现为加强肋两侧应力集中发生撕裂，这一现象在此工况中产生的原因可能是水射流载荷强度在0.15 m爆距下达到最大，射流的毁伤作用较强；爆距为0.2 m以上时冲击波的作用效果较弱，未能使圆柱壳发生大塑性变形，随后圆柱壳在气泡脉动和射流载荷的作用下产生了局部凹陷，此凹陷的大小和深度随着爆距的增大而减小。

图12为圆柱壳迎爆面分别在冲击波、气泡脉动与射流载荷下的单元应力峰值和挠度随爆距变化情况。由图12可见：在冲击波阶段，随着爆距的增大，冲击波载荷在迎爆面单元上产生的应力以及迎爆面的挠度均呈下降趋势，挠度在爆距增大到0.2 m时的下降趋于平缓，且趋近于0 m，表明在0.2 m爆距下，冲击波对在圆柱壳上作用产生的变形很小；气泡脉动及水射流载荷作用产生的单元应力和挠度随爆距变化均呈现出先增后减的趋势，与图9中的压力及流场速度变化趋势一致。

3.1.4 不同爆距下圆柱壳毁伤模式分析

圆柱壳结构在水下爆炸载荷作用下的毁伤模式受到爆距的影响，27 g的TNT炸药对壁厚为3 mm圆柱壳在不同爆距下的毁伤情况有非常明显的区别。对于冲击波载荷，其载荷峰值随爆距的增长呈指数衰减，在0.05 m爆距时冲击波载荷作用下圆柱壳的毁伤模式为局部大凹陷，爆距从0.05 m变化到0.2 m过程中，冲击波载荷在圆柱壳上造成的凹陷变形效果也逐渐减弱，从大凹陷变形过渡为小幅凹陷变形直至在0.2 m爆距下无凹陷产生，大于这一爆距时冲击波载荷将不能在圆柱壳上产生毁伤效果。在气泡脉动阶段，气泡脉动载荷及水射流载荷的联合作用对圆柱壳造成了二次毁伤效果，在爆距小于0.15 m时，气泡脉动载荷及水射流载荷进一步扩大了圆柱壳中部的凹陷，并使圆柱壳整体产生了小幅的弯曲变形；爆距为0.15 m时由于水射流载荷达到最大化，圆柱壳凹陷区域在冲击作用下出现了破口；爆距大于0.15 m时，气泡脉动载荷及水射流载荷的作用在圆柱壳中部造成凹陷变形，且凹陷程度随爆距的增大而减弱，在爆距达到0.3 m时仅产生轻微凹陷。同时，圆柱壳在水下爆炸载荷作用下的毁伤模式满足一定的相似准则，在TNT药包药量、爆距、圆柱壳尺寸参数等相关参数按几何相似律变化时，其他尺寸圆柱壳的毁伤模式可以通过本文中的结果进行预测。

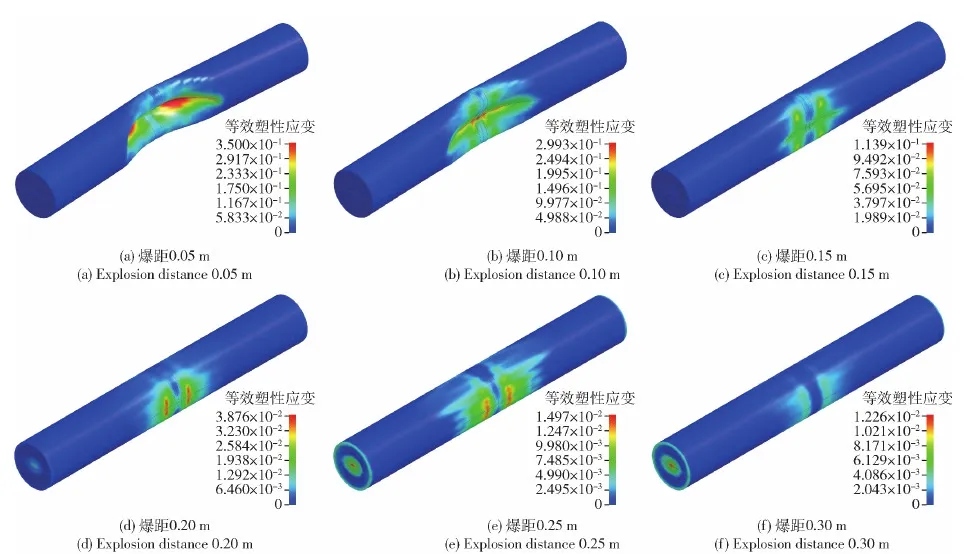
图10 不同爆距下圆柱壳结构在冲击波作用下的塑性应变情况Fig.10 Plastic strain of the cylindrical shell induced by shock wave under different explosion distances

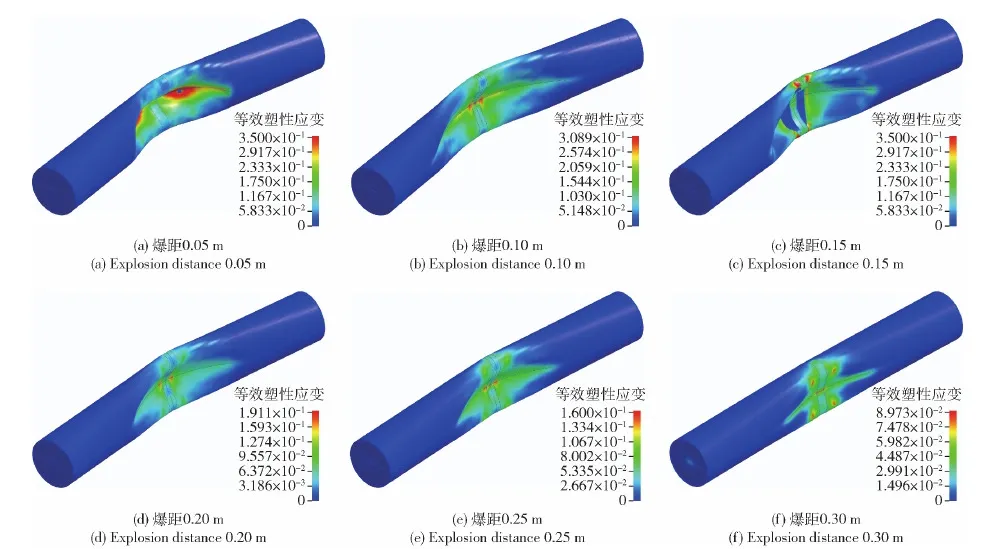
图11 不同爆距下圆柱壳结构在冲击波及气泡载荷作用下的塑性应变情况Fig.11 Plastic strain of the cylindrical shell induced by shock wave and bubble load under different explosion distances

图12 圆柱壳迎爆面峰值应力、挠度随爆距变化情况Fig.12 Variation of peak stress and peak deflection of the cylindrical shell induced with the explosion distance

3.2 不同方位下冲击波和气泡载荷对圆柱壳的作用效果

保持TNT装药量、水深大小、边界条件不变，改变TNT药包与圆柱壳之间的方位，研究不同方位下冲击波和气泡载荷对圆柱壳的作用效果。

3.2.1 工况设置

设置TNT药量为27.0 g，爆炸深度2.7 m，爆距为0.1 m，调节药包相对于圆柱壳的方位，得到3组不同工况如表7所示。

如图13所示，工况1为基本工况，工况2表示将药包从圆柱壳正下方0.1 m处移至正上方0.1 m处，工况3表示将药包移至与圆柱壳同一水平高度处，且在水平方向上与圆柱壳的距离为0.1 m。

表7 计算工况Table 7 Calculation conditions

图13 TNT药包位于圆柱壳不同方位的示意图Fig.13 Schematic diagram of different charge positions

3.2.2 不同方位下爆炸毁伤结果分析

图14所示为不同方位下的圆柱壳变形情况，图15为圆柱壳迎爆面单元挠度随时间变化情况。如图15所示，在冲击波作用下迎爆面挠度曲线重合，在气泡脉动及射流载荷联合作用下的挠度变化有所差异，药包位于圆柱壳下方时最大，上方时最小；3种工况下的变形均表现为局部大凹陷以及整体的小幅弯曲。药包方位对气泡的形态演化产生了一定的影响作用，当药包位于圆柱壳下方时，气泡在圆柱壳的影响下拉伸为两部分，同时产生朝向圆柱壳的水射流，速度较大；药包位于上方时，气泡演化呈现为水母状，气泡在浮力的作用下向上运动，逐渐与圆柱壳背离，产生的朝向圆柱壳的水射流速度较小，强度较弱；当药包位于侧方时，气泡的形态介于前二者之间，呈现为尾部较长的水母状，产生的水射流强度介于前二者之间。

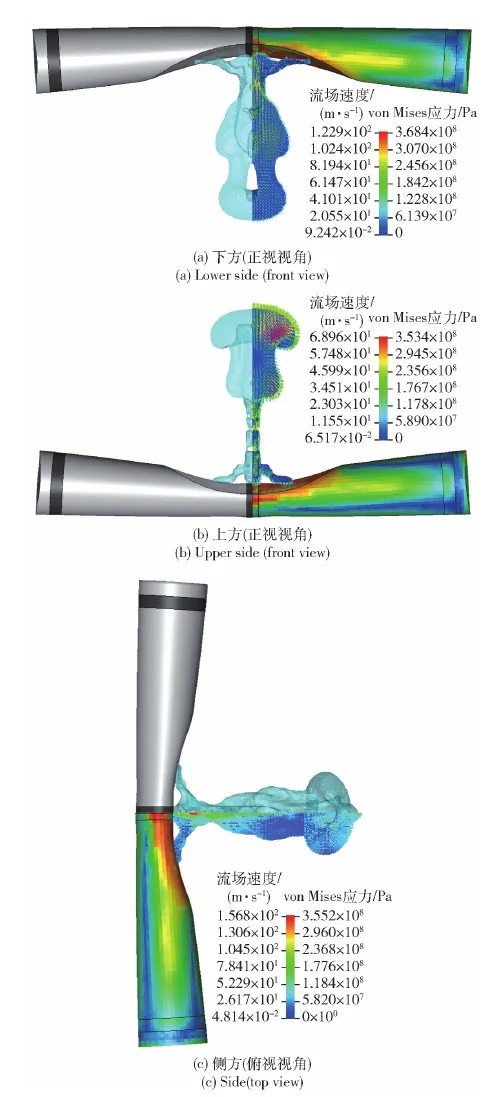
图14 不同方位下爆炸气泡对圆柱壳的作用效果Fig.14 Interaction between the explosive bubble and the cylindrical shell under different charge positions

图15 不同方位下迎爆面单元挠度变化情况Fig.15 Variation of explosion surface deflection with charge position

取圆柱壳迎爆面上的单元以及TNT药包和圆柱壳之间距离爆点0.1 m位置的观察点，对爆炸载荷下的圆柱壳迎爆面压力及流场速度变化情况进行分析，得到曲线如图16所示。由图16可见：3个工况下冲击波阶段压力曲线基本重合，流场速度曲线变化规律也基本一致；后期气泡脉动及射流载荷联合作用所产生的迎爆面压力和流场速度有所不同，药包位于圆柱壳下方的工况的迎爆面压力和流场速度明显较大，这也是此工况气泡脉动和射流载荷能使圆柱壳产生较大挠度的基础。

图16 迎爆面单元压力及TNT药包0.1 m处观察点流场速度随时间变化情况Fig.16 Pressure on the explosion face and velocity of the flow field at the observation point with time

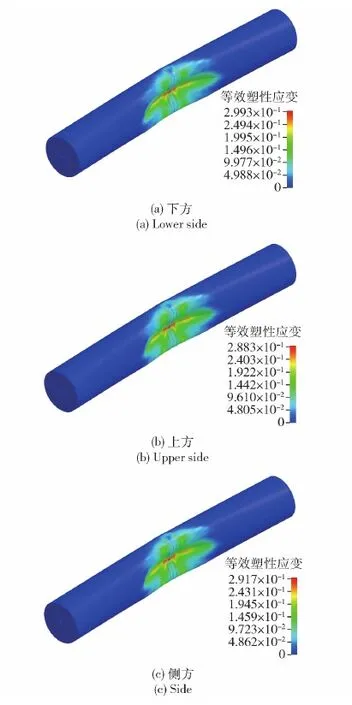
图17 不同方位下圆柱壳结构在冲击波载荷作用下的塑性应变情况Fig.17 Plastic strain of the cylindrical shell induced by the shock wave load under different charge positions

图17为不同方位下圆柱壳结构在冲击波载荷作用下的塑性应变情况。由图17可见，在冲击波作用下，3种工况的圆柱壳结构变形响应情况基本一致，均表现为中部的凹陷变形。图18为不同方位下的圆柱壳结构迎爆面单元应力、塑性应变随时间变化情况。通过图18(a)可以看出，3种工况下冲击波载荷作于圆柱壳使其产生的单元应力峰值大小均相等，单元应力随时间变化曲线在冲击波阶段重合，且在这一阶段圆柱壳产生的塑性应变基本相同。

图19为不同方位下圆柱壳结构在冲击波及气泡载荷作用下的塑性应变情况。由图19可见：气泡脉动载荷及射流载荷进一步扩大了圆柱壳中部的凹陷，并使其整体产生了弯曲变形；气泡脉动载荷及射流载荷联合作用下圆柱壳结构的单元应力变化规律与冲击波阶段不同，药包位于圆柱壳下方的工况的单元应力峰值明显大于其他两个工况，且这一工况下圆柱壳最终产生的塑性应变最大，而药包位于圆柱壳上方的工况中圆柱壳单元应力峰值和最终塑性应变最小，如图18(b)所示。以上规律与图15中的挠度变化情况一致。

图18 不同方位下的圆柱壳结构迎爆面单元应力、塑性应变随时间变化情况Fig.18 Variation of stress and plastic strain of the explosion surface with charge position

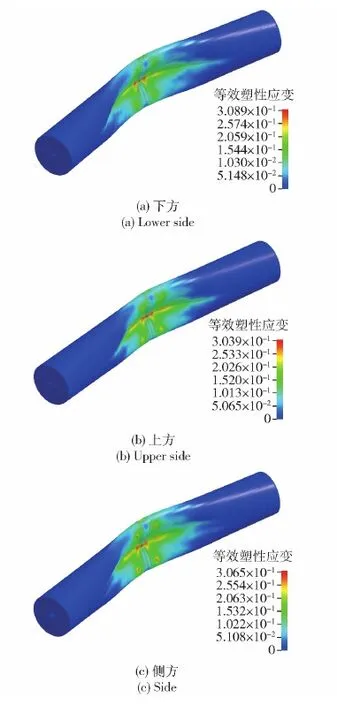
图19 不同方位下圆柱壳结构在冲击波及气泡载荷作用下的塑性应变情况Fig.19 Plastic strain of the cylindrical shell induced by shock wave and bubble load under different charge positions