基于深度学习的黄土干湿循环损伤分析
2023-03-21
(西安科技大学 建筑与土木工程学院,西安 710054)
1 研究背景
黄土作为特殊土的一种,广泛分布于我国西北、华北和东北地区。黄土的组成成分多样,含有多种氧化物,以SiO2为主,然后是Al2O3、CaO,其次为Fe2O3、MgO和K2O等。黄土颗粒之间较为疏松,含有许多可溶性物质,使其具有多孔性[1]、垂直节理[2]和湿陷性[3]等特殊性质。在工程建设中黄土往往容易被流水侵蚀,破坏其原有的结构,导致塌方[4]、滑坡[5]和不均匀沉降[6]等各种问题。当气候处于旱季时,黄土较为干燥,而气候处于雨季时黄土较为湿润,旱-雨季类型的干湿循环对黄土造成循环性风化损伤破坏。在这个干湿循环过程中,黄土原有颗粒的尺寸、位置和组成成分均发生改变,宏观上导致黄土的抗剪强度、渗透性和压缩模量产生改性[7]。
干湿循环条件下的土壤微观结构变化规律,可通过扫描电镜、X射线衍射和核磁共振技术等技术从物理层面直观描述。Liu等[8]试验研究了干湿循环对压实低塑性黏土基质吸力和体积特性的影响,发现随着循环次数的增加,干湿循环下土壤保水曲线(SWRC)的位置向下移动。Chen等[9]进行直接剪切试验以研究多个干湿循环对不饱和压实黏土剪切行为的影响。Chu等[10]通过扫描电镜和压汞法研究了干湿循环对改性膨胀土的膨胀行为和可压缩性的影响,膨胀土微观结构表现出退化趋势。Liu等[11]通过电镜扫描发现在粉质黏土干燥/湿润循环过程中,土壤颗粒被拉近,导致微观结构的变化,从而导致力学行为的改变。
叶万军等[12]通过干湿循环试验揭示细微观结构变化与宏观力学性质的相关关系,并区分古土壤与黄土间存在的差异性。赵贵涛等[13]通过压汞试验研究冻融循环、干湿循环和交替的干湿-冻融循环对压实膨胀土的微观结构、土-水特征曲线和收缩特征曲线的影响。胡长明等[14]通过电镜扫描从微观角度研究干湿循环引起的压实黄土强度劣化,同时采用ABAQUS数值模拟分析干湿循环作用下压实黄土填方边坡稳定性。万勇等[15]从微观层次揭示了压实黏土在干湿循环作用下的变形特性和强度衰减内在本质。袁志辉等[16]采用单轴拉伸法对干湿循环条件下黄土抗拉强度进行试验研究,多次的干湿循环作用打破了原状黄土的原有结构,使得其抗拉结构强度消失。目前土壤干湿循环损伤处于试验探索阶段,其理论尚不完善,基于土壤微观纹理建立土壤干湿循环损伤理论迫在眉睫。
本文采用灰度共生矩阵法[17],利用陕西西安地区的黄土电镜扫描图片提取黄土微观纹理特征,通过建立基于长短期记忆网络(LSTM)[18]的深度学习时序回归预测模型描述黄土纹理特征和土壤微观裂纹与孔隙占比之间的联系,依据干湿循环损伤模型计算土壤干湿循环损伤因子,揭示土壤微观结构在干湿循环过程的变化规律。
2 试验过程
2.1 试验材料
试验用土为取自陕西西安地区的黄土,气候为暖温带半湿润大陆性季风气候,在施工季土壤干湿循环较为频繁,其基本性质如表1所示。
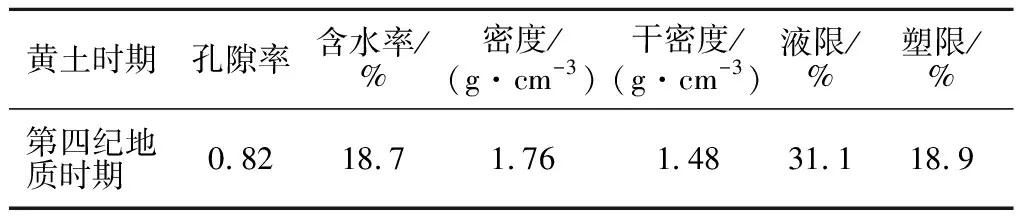
表1 西安试验黄土基本性质Table 1 Basic properties of Xi’an loess for experiment
2.2 试验装置
试样微观结构试验装置采用荷兰飞纳Phenon/pro台式扫描电子显微镜,如图1所示,其SEM分辨率优于14 nm,放大倍数区间为80~130 000,采用背散射电子探测器。

图1 扫描电子显微镜Fig.1 Scanning electron microscope(SEM)
2.3 试验方案
采用胶头滴管将水滴滴在试样的滤纸上以均匀湿润土壤,再将土壤试样密封静置48 h,此时土壤试样含水率达到设定状态。将湿润土样置于恒温烘箱进行干燥,当含水率达到16%可认为土壤试样处于干燥状态,视为土壤进行了一次干湿循环。通过滴入滤纸的水滴数量控制土样的含水率,试验土壤含水率控制在16%~24%,将土壤试样分别编号为1组、2组,分别进行0次、1次、2次、4次和6次干湿循环试验,用美工刀将试样修剪成1 cm3的试块在喷金处理后进行电镜扫描。将试样分别放大500、2 000、5 000倍,得到3组电镜扫描照片。
3 试验结果及分析
3.1 灰度共生矩阵
电镜扫描图像灰度在空间位置上的分布反映了土壤试样的微观纹理结构,扫描图像的灰度空间相关特性可以用来描述土壤试样微观纹理结构在干湿循环条件下的变化规律。灰度共生矩阵是对土壤电镜扫描图像中固定距离的两像素具有某种灰度进行的统计,可用来描述土壤试样图像灰度的空间相关特性。
可通过编程读取电镜扫描灰度图像,可表示为f(x,y),则反映该图像灰度一定空间关系的灰度共生矩阵P为
P(g1,g2)=

(1)
式中:#为求集合中的元素个数;S为土壤图像中一定空间关系的像素对集合;等号右边分子为满足一定空间关系的像素对灰度分别为g1和g2的个数;分母为电镜扫描图像的像素对总个数。在求解土壤试样图像的灰度共生矩阵时,设置两像素之间的距离为1保持不变,两像素之间的角度选取0°、45°、90°、135°。
在具体进行土壤试样微观纹理结构的评价时,选取5个指标作为土壤试样灰度图像的纹理特征统计值,分别为对比度、相关性、熵、平稳度和二阶矩。
其中对比度CON计算公式为
(2)
式中:i与j分别为相邻像素的灰度;P(i,j)为相邻像素灰度差为|i-j|的像素分布概率。灰度图像对比度反映了土壤试样灰度图像的微观纹理结构深浅的程度,是对黄土试样内部微观裂纹和颗粒孔隙深浅程度的描述,灰度图像对比度越大,则说明微观裂纹和孔隙深度越深。
相关性COR的计算公式为
(3)
其中:
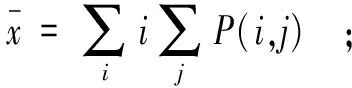

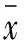
熵ENT的计算公式为

(4)
土壤试样电镜扫描灰度图像熵描述了土壤试样微观结构纹理在二维灰度图像中的空间分布状况,当土壤试样微观裂纹和孔隙数量增多时,土壤试样微观纹理结构趋于破坏和混乱化,土壤试样灰度图像熵变大。
平稳度IDM的计算公式为
(5)
土壤试样灰度图像平稳度反映了土壤试样微观纹理结构的粗糙程度,土壤试样微观裂纹与孔隙在二位灰度图像中截面积越大,灰度连续性越强,则平稳度越大。
二阶矩ASM的计算公式为
(6)
土壤试样灰度图像二阶矩描述了土壤试样微观纹理均匀程度状态,二阶矩越小则说明土壤试样灰度图像灰度共生矩阵灰度越接近,结构纹理比较细致。灰度图像二阶矩随土壤干湿循环的变化反映了土壤微观裂隙和孔隙的变化状态,随着裂隙和孔隙的增大,二阶矩也逐渐变大。
3.2 选择合适的电镜扫描图像放大倍数
电镜扫描图像可以将土壤试样放大不同的倍数,选取合适的放大倍数对基于灰度共生矩阵的土壤试样微观结构分析至关重要。以1组未进行干湿循环的土壤试样为例,电镜扫描图像如图2所示,土壤呈现团粒结构,多为针孔状孔隙,含钙质条纹及少量钙质结核。通过编程求取土壤电镜扫描图像的灰度共生矩阵,计算灰度图像的对比度、相关性、熵、平稳度和二阶矩,如图3所示。

图2 不同放大倍数的电镜扫描图像Fig.2 SEM images with different magnifications
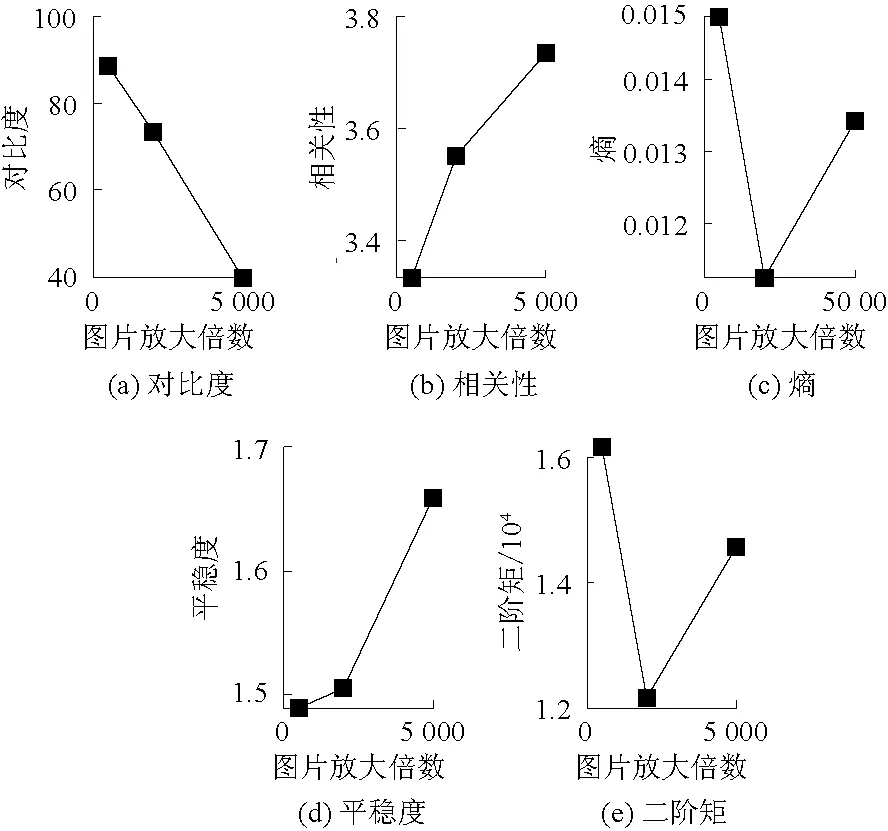
图3 灰度共生矩阵各指标量与放大倍数的关系Fig.3 Relations between indices of gray level co-occurrence matrix and magnification
一般来说,灰度图像指标随图像放大倍数的变化规律呈现一致性,而图3中指标量熵和二阶矩出现突变现象,在放大倍数为5 000倍时突然增大,是由于图像放大倍数过大,所计算指标过于局部,使计算结果过小。但若只放大500倍,又显得放大倍数过小,难以将干湿循环过程中土壤试样颗粒和孔隙发展规律表现出来,因此对干湿循环条件下土壤微观结构机理的研究采用放大倍数为2 000倍的电镜图像。
从图3可知熵和二阶矩的发展趋势较为相似,对5个指标量相关性进行分析,结果如表2所示。熵和二阶矩相关性显著,在进行土壤试样干湿循环微观结构机理研究时,本文只选取指标量熵进行分析。
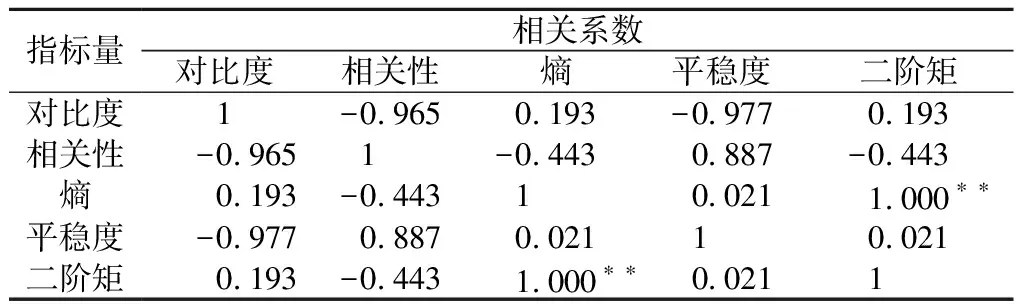
表2 灰度共生矩阵指标量之间的相关关系
3.3 干湿循环条件下灰度指标变量变化
将1组土壤试样电镜扫描图像放大倍数设定为2 000倍,在0、1、2、4、6次干湿循环条件下,土壤试样灰度图像如图4所示。

图4 不同干湿循环次数下土壤试样灰度图像Fig.4 Gray-scale images of loess samples undergone different dry-wet cycles
根据试样灰度图计算土壤试样图像灰度共生矩阵指标量,如图5所示。图5中土壤试样指标量对比度随着干湿循环次数的增加从74.186 5减小到37.684 5,呈现反“S”型曲线,减小速度逐渐增大后又逐渐减小。土壤试样结构纹理逐渐变浅,是由于干湿循环过程中土壤试样水分会产生迁移和蒸发现象,不断冲刷土壤试样团粒致使土壤试样整体纹理变浅。
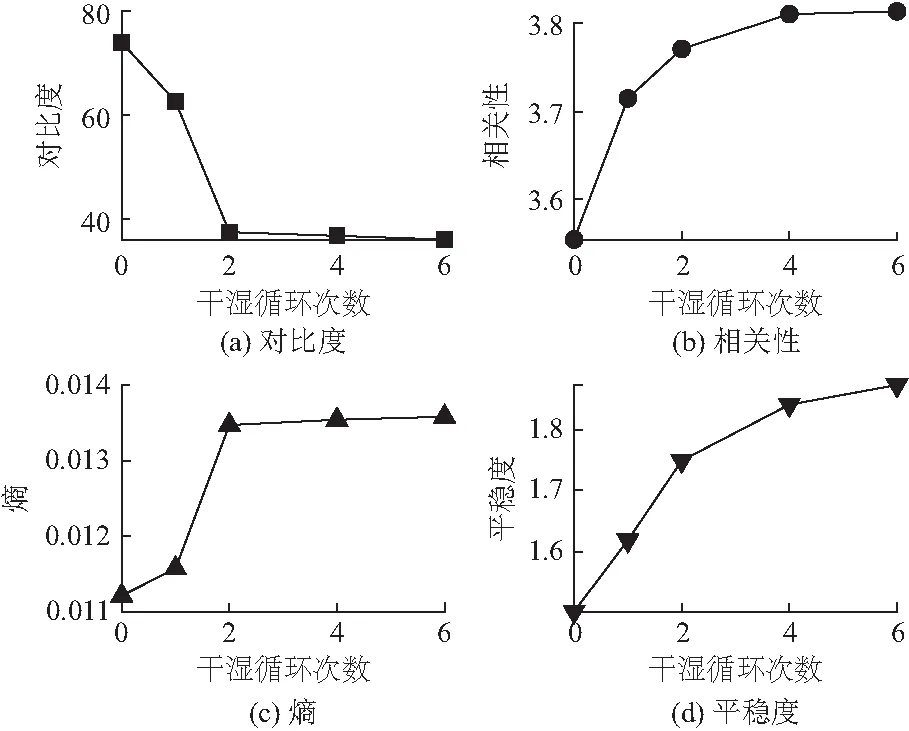
图5 指标量随干湿循环次数变化Fig.5 Changes of gray index quantities with the number of dry-wet cycles
灰度共生矩阵指标量相关性从3.56增加到3.81,增加速度逐渐减小,表明土壤试样的纹理走向随干湿循环次数的增加逐渐明显,说明在干湿循环过程中土壤试样原有微观裂纹和孔隙在水分迁移的不断冲刷下不断扩大,与此同时在水气的转化作用下土壤试样又不断产生新的微观裂纹和孔隙,使土壤试样变得更加蓬松,在水分迁移冲刷作用下土壤试样中形成了沿原有水分迁移通道的纹理走向。
试样灰度共生矩阵指标量熵随干湿循环次数的增加呈现“S”走向,从0.011增加到0.014,表明土壤试样微观结构纹理复杂度增加。在干湿循环过程中,在土壤水分的迁移冲刷下试样微观裂纹和孔隙数量和大小增加,土壤试样团粒结构边缘不断圆润,颗粒丰度不断提高,纹理结构复杂度不断增大。
随着干湿循环次数的增加,土壤试样灰度共生矩阵指标量平稳度不断增大,这表明随着干湿循环次数的增加,土壤试样灰度图像中灰度较为连续,在图像不同区域之间微观裂纹和孔隙变化逐渐趋于均匀化,这是由于干湿循环过程中水分的迁移和蒸发使得在原试样中未产生微观裂纹和孔隙的区域不断产生新的微观裂纹和孔隙,使得土壤试样微观裂纹和孔隙在二维灰度图像的分布中趋于均匀化,土壤试样不同区域间都出现或多或少的水分迁移通道,土壤试样中的针状孔隙之间彼此连通,出现条形孔隙,如图4所示。相关性和平稳度沿凸曲线发展,在5次干湿循环后达到极值。
3.4 干湿循环条件下土壤孔隙面积测量
对放大2 000倍的土壤电镜扫描图像进行伪彩色处理,增强图像中土壤微观裂纹和孔隙与土壤团粒的对比显示效果,如图6所示。随着干湿循环次数的增加,土壤中原有的微观裂纹和针状孔隙不断受到水分迁移的冲刷,彼此间逐渐连通形成较大的土壤微观裂纹,土壤纹理更加浅显。土壤中水分的迁移将土壤团粒周围的分散颗粒冲刷到一起形成新的土壤颗粒。土壤中原有结构的点-点接触、点-边接触、边-边接触、边-面接触和面-面接触在干湿循环过程中持续发育,土壤团粒边缘由尖锐变得圆润。
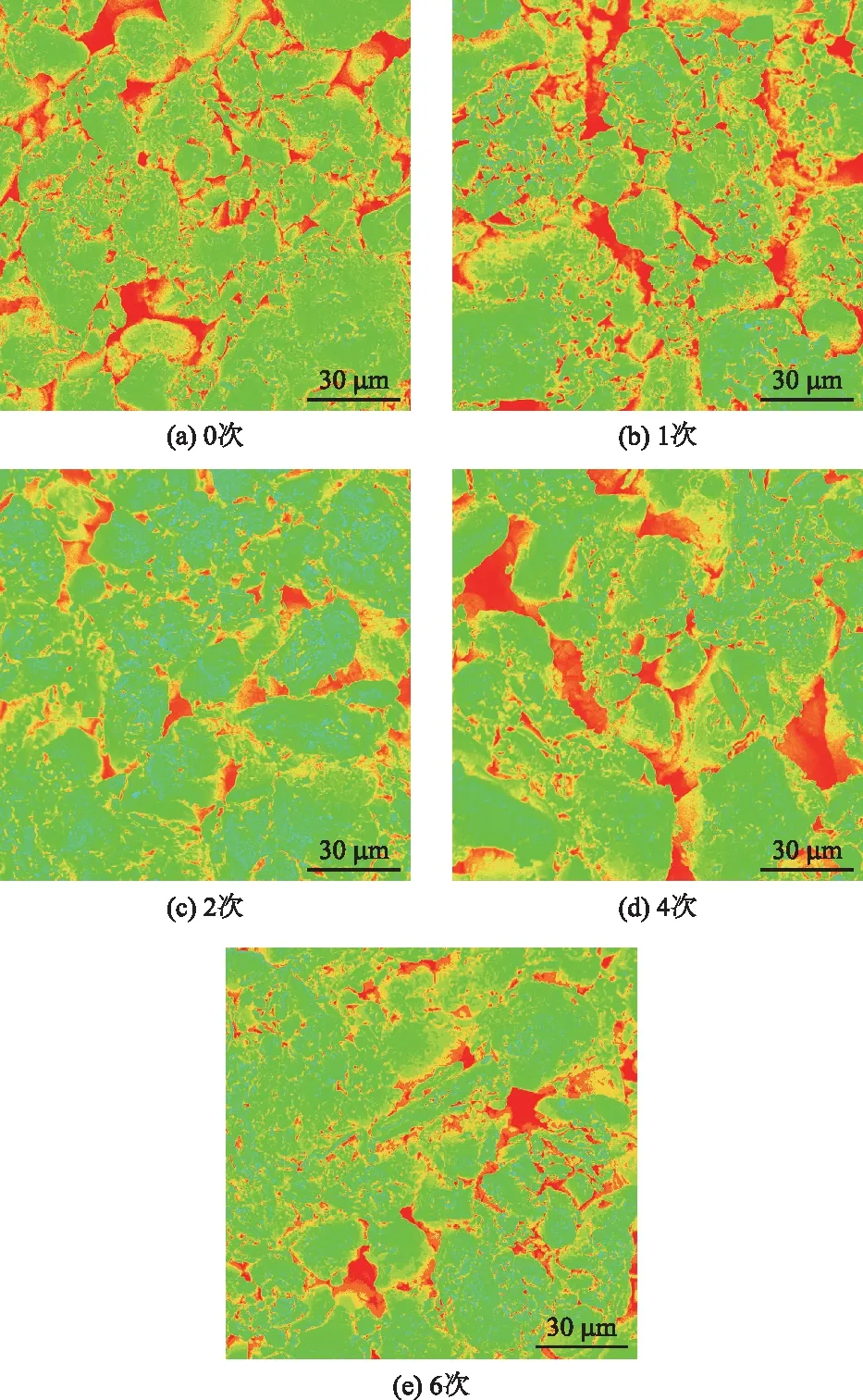
图6 不同干湿循环次数下土壤试样伪彩色图像Fig.6 Pseudo-color images of loess samples undergone different dry-wet cycles
将伪彩色图像变为图像分割模式,将灰度分布概率密度最大处定为土壤微观裂纹和孔隙面积阈值,提取土壤微观裂纹和孔隙面积,将已提取土壤微观裂纹和孔隙面积的土壤图像转换为二值化图像,如图7所示,红色部分为土壤微观裂纹和孔隙区域,灰色部分为土壤颗粒。由图7中红色部分的发展趋势可以看出,随着干湿循环次数的增加,土壤原有结构在水分迁移作用下被破坏并且形成新的结构,原始细小深刻的微观裂纹和孔隙变得更加宽大浅显,散乱分布的土壤细小颗粒在水分迁移的冲刷下集中到一起形成新的土壤颗粒,使得土壤中原有颗粒变得圆润,土壤纹理发育得成熟。
提取图7中前4次干湿循环的微观裂纹和孔隙像素面积,计算土微观裂纹和孔隙部分在土壤扫描部分的占比,其随干湿循环次数的关系曲线如图8所示。随着干湿循环次数的增加,土壤试样微观裂纹与孔隙的占比逐渐增加,从最初67.12%经历4次干湿循环后增加到74.83%,在第6次干湿循环时土壤微观裂纹与孔隙占比达到75.45%,增加速度不断减小。在5次干湿循环后,其纹理性基本不再增强,说明土体纹理化已经完成。
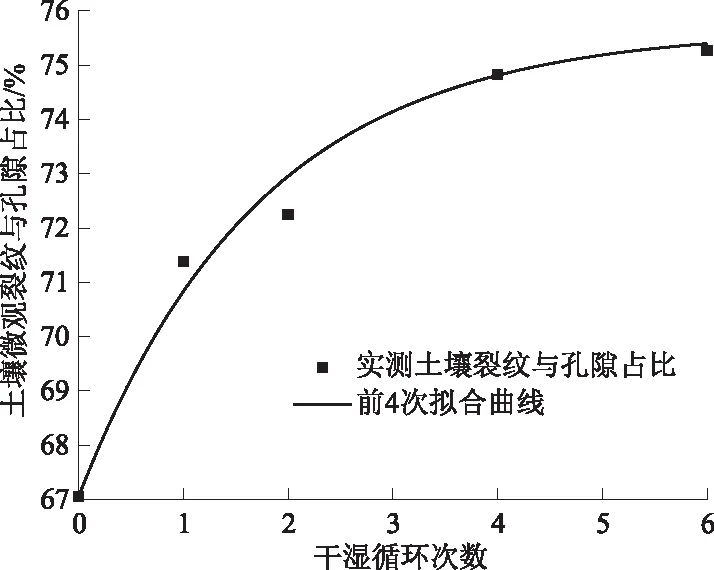
图8 土壤微观裂纹和孔隙占比与干湿循环次数关系Fig.8 Relationship between the proportion of soil cracks and pores and the number of dry-wet cycles
4 干湿循环条件下黄土损伤分析
4.1 干湿循环条件下黄土损伤模型
随着干湿循环次数的增加,土壤原有结构被破坏,不断有新的微观裂纹和孔隙产生,旧有微观裂纹和孔隙继续发育,土壤结构纹理变得宽大浅显。干湿循环对土壤结构的损伤微细观方面主要表现在土壤微观裂纹和孔隙面积增加,宏观方面则主要表现在土壤强度的减小。土壤微观裂纹和孔隙面积占比在一定程度上可以反映干湿循环对土壤原有结构的损伤,为此建立黄土干湿循环损伤模型。对各灰度图像指标量进行拟合,得到各灰度指标量随干湿循环次数增加的变化规律f(n)(n为干湿循环次数),对土壤微观裂纹和孔隙面积占比随干湿循环次数的变化曲线同样进行拟合,得到土壤微观裂纹和孔隙面积占比随干湿循环次数增加的变化规律y(n)。
以干湿循环次数为时间轴,采用LSTM深度学习算法建立土壤试样灰度图像指标量和土壤微观裂纹和孔隙面积占比之间的时序回归预测模型,得到土壤微观裂纹和孔隙面积占比随灰度图像指标量的变化规律,如式(7)所示。
y=φ(f1(n),f2(n),f3(n),f4(n)) 。
(7)
式中fi(n)为对应的4个灰度图像指标变量关于干湿循环次数n的拟合函数。
土壤微观裂纹和孔隙面积占比拟合曲线表明土壤在未进行干湿循环时本身已存在微观裂纹和孔隙,说明土壤存在初始损伤。实际上,未进行干湿循环的土壤的压力强度是基于初始损伤条件下得出的。土壤微观裂纹和孔隙面积占比变化导致了土体应力强度的变化。土体有效应力与应力之比为
(8)
式中:土体应力σ=P/S;土体有效应力σ′=P/S′;P为土体微元受到的压力;S为无损土体截面积;S′为有损土体截面积。
土体干湿循环有效应力与土体未进行干湿循环有效应力之比为
(9)
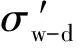
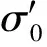
根据式(10)定义土壤干湿循环损伤因子D为
(11)
4.2 干湿循环损伤时序回归预测
以1组黄土试样为例,前4次干湿循环灰度指标量拟合曲线如图9所示。在前2次干湿循环中,试样对比度和熵发生剧烈变化,说明土体中微观裂纹和孔隙迅速增加。土壤干湿循环过程可以分为两阶段:微观裂纹和孔隙增加、土壤结构纹理化。第1个阶段主要在前2次干湿循环内发生,第2个阶段主要发生在前5次干湿循环内。

图9 灰度图像指标量拟合曲线Fig.9 Fitted curves of gray image index quantities
按0~12次干湿循环分成1 201个点,按照拟合曲线可得到灰度指标量和土壤微观裂纹和孔隙面积占比的1 201个数据。同时建立深度学习时序回归预测模型,包含LSTM层、全连接层和丢弃层。其中LSTM层具有200个隐含单元,全连接层大小为50,丢弃层丢弃概率为0.5。以0.01的学习率,小批量为220进行300轮训练,梯度阈值为1,以1组土壤试样灰度图像指标变量和土壤微观裂纹与孔隙占比作为训练集合,输入2组土壤试样灰度图像指标量,对土壤微观裂纹和孔隙占比进行时序回归预测。
第2组土壤试样损伤因子深度学习时序回归预测曲线与实际土壤损伤因子变化曲线如图10所示。
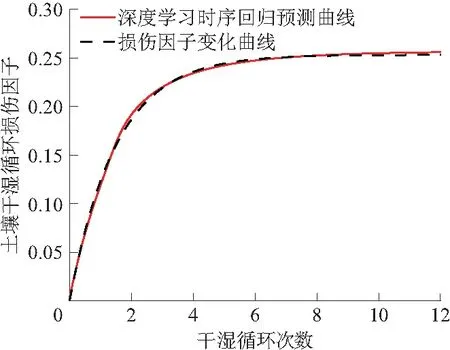
图10 土壤损伤因子变化曲线Fig.10 Change curve of loess damage factor
深度学习时序回归预测曲线与实际土壤损伤因子变化曲线吻合度较高,干湿循环深度学习模型具有较好的可靠性。第1组第6次干湿循环损伤因子为0.249,深度学习预测曲线第6次损伤因子为0.246,可见,深度学习结果与第1组实测数据相比也较为贴合。随着土壤干湿循环次数的增加,土壤损伤因子逐渐增大。土壤试样经历4次干湿循环后干湿循环损伤因子损伤比例达到93.10%。在6次干湿循环后,土壤损伤因子增加速度几乎为0,趋近于极限值0.253。在干湿循环过程,土壤试样内部水分出现迁移现象,会产生水分迁移通道,在土壤试样中形成新的微观裂纹和孔隙,土壤中的微观裂纹和孔隙占比不断增大,在6次干湿循环后土壤中微观裂纹和孔隙占比增加到一个极限值。此时,在干湿循环损伤作用下土壤颗粒只进行重组,土壤试样不再产生新的微观裂纹和孔隙,干湿循环不再对土壤试样产生损伤作用。
5 结 论
本文对西安地区的黄土进行干湿循环处理,基于灰度共生矩阵利用黄土试样电镜扫描灰度图像提取土壤纹理特征数据,分析土壤微观结构变化。以灰度图像最大概率密度分布的灰度为阈值计算土壤微观裂纹和孔隙占比,通过深度学习时序回归预测模型建立土壤纹理特征数据和土壤微观裂纹和孔隙占比之间的联系,根据建立的数学模型计算土壤干湿循环损伤程度,得到如下结论:
(1)黄土试样灰度图像在放大2 000倍时能够反映黄土干湿循环后微观结构变化。经过对比,灰度指标量熵和二阶矩呈现显著相关性,对比度随干湿循环次数成反“S”型曲线,熵呈“S”型曲线发展,经过2次干湿循环后达到极限值,相关性和平稳度沿凸曲线发展,在5次干湿循环后达到极值。
(2)在干湿循环后,对比度减小,相关性、熵和平稳度不断增大,说明土壤试样微观裂纹和孔隙不断增大,纹理性不断增强。在2次干湿循环后土壤试样中基本不再产生新的微观裂纹和孔隙,土壤颗粒之间只是重复进行重组,形成干湿循环中与水分迁移方向趋向平行的纹理走向,在5次干湿循环后纹理性基本不再增强。
(3)建立灰度指标变量和土壤试样微观裂纹和孔隙占比深度学习时序回归预测模型,可以较好地反映土壤的干湿循环损伤,经6次干湿循环后,干湿循环的损伤趋近损伤极限值0.253,说明土壤的干湿循环损伤是有限的,在6次干湿循环后损伤不再增大。
(4)土壤干湿循环损伤分为两个阶段:微观裂纹和孔隙增加、土壤结构纹理化。第1个阶段主要在前2次干湿循环内发生,第2个阶段主要发生在前5次干湿循环内。
